20.1.2.1中位数和众数 课件(共26张PPT)
文档属性
| 名称 | 20.1.2.1中位数和众数 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 19:35:18 | ||
图片预览







文档简介
20.1.2.1
中位数与众数
第二十章
数据的分析
2021年春人教版八年级(下)数学
上节课我们学均数,知道它可以作为一组数据的代表,利用它可以反映一组数据的集中趋势.
除了平均数,还有什么样的数也可以来作为一组数据的代表,反映一组数据的集中趋势呢?
导入新课
1.理解中位数、众数的意义.
2.会利用样本的中位数去估计总体的中位数.
3.体会中位数和众数在统计中的作用.
重点:认识中位数、众数的意义,并会找一组数据的中位数和众数.
难点:利用中位数、众数分析数据信息做出决策.
学习目标
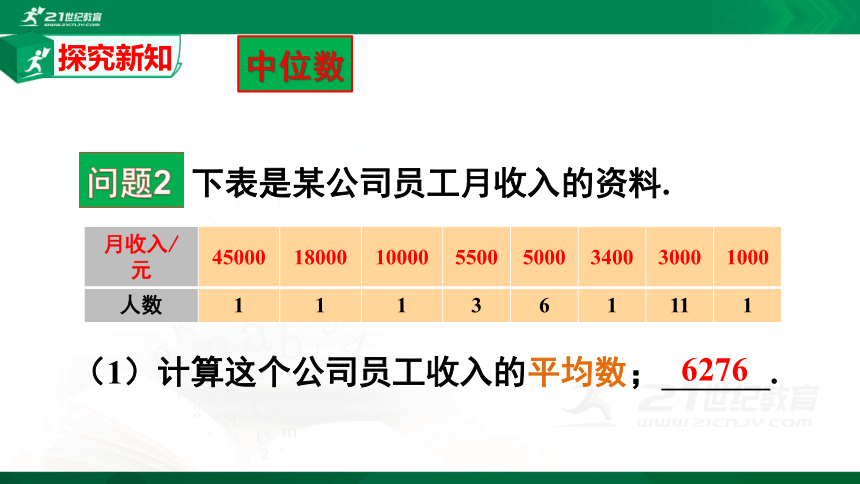
中位数
下表是某公司员工月收入的资料.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入/元
45000
18000
10000
5500
5000
3400
3000
1000
人数
1
1
1
3
6
1
11
1
(1)计算这个公司员工收入的平均数;
.
6276
问题2
探究新知
从上表可以看出平均数远远大于绝大多数人(22人)的实际月工资,绝大多数人“被平均”,不合适.
怎样准确的反映公司全体员工月收入水平?
(2)若用(1)算得的平均数反映公司全体员工月收入水平,你认为合适吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入/元
45000
18000
10000
5500
5000
3400
3000
1000
人数
1
1
1
3
6
1
11
1
采用中位数
1.什么叫中位数?怎样确定一组数据的中位数?
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数据就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
不一定出现在这组数据中
一组数据的中位数是唯一的
探究新知
2.中位数反映的是一组数据的什么特征量?
反映了一组数据的集中趋势.
3.求下列数据的中位数.
(1)-2,0,-5,4,3,1;
(2)54,28,13,47.
答案:0.5
答案:37.5
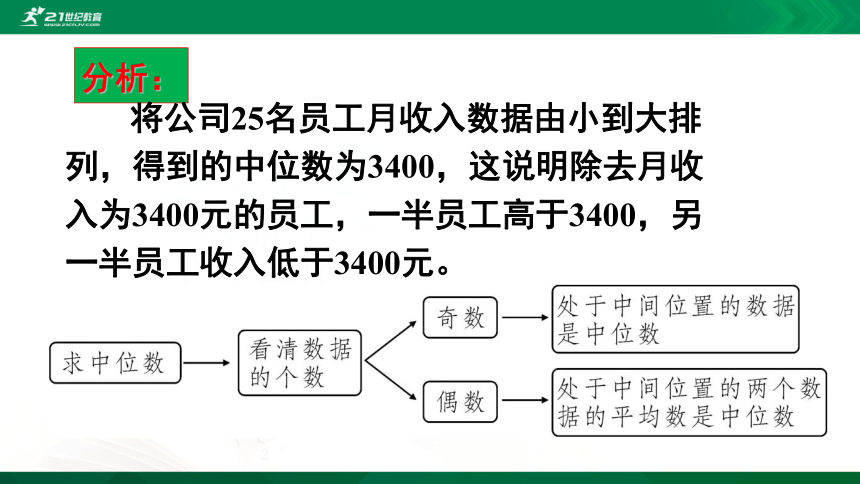
分析:
将公司25名员工月收入数据由小到大排列,得到的中位数为3400,这说明除去月收入为3400元的员工,一半员工高于3400,另一半员工收入低于3400元。
例4
在一次男子马拉松长跑比赛中,抽得12名选手所用的时间(单位:min)如下:
136
140
129
180
124
154
146
145
158
175
165
148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142min,他的成绩如何?
例题讲解
解:(1)先将样本数据按照由小到大的顺序排列:
124
129
136
140
145
146
148
154
158
165
175
180
这组数据的中位数为处于中间的两个数146,148,即
因此样本数据的中位数是147.
(2)由(1)知样本数据的中位数为147,它的意义是:这次马拉松比赛中,大约有一半选手的成绩快于147min,有一半选手的成绩慢于147min.
这名选手的成绩是142min,快于中位数147min,因此可以推测他的成绩比一半以上选手的成绩好.
根据例4中的样本数据,你还有其他方法评价(2)中这名选手在这次比赛中的表现吗?
下面的条形图描述了某车间工人日加工零件数的情况.
请找出这些工人日加工零件数的中位数,并说明这个中位数的意义.
针对练习
解:由条形图知这组数据中从小到大排列为:4个3,5个4,8个5,9个6,6个7,4个8共36个数,则这组数据的中位数为处在中间两个数6,6的平均数,因此这些工人日加工零件的中位数为6.
这个中位数的意义:根据这个中位数,可以估计其车间工人日加工零件个数大于或小于这个数的人数各占一半.
众数
众数:一组数据中出现次数最多的数据.
众数反映了一组数据的集中趋势,当众数出现的次数越多,它就越能代表这组数据的整体状况.但当各数据重复出现的次数大致相等时,众数往往就没有什么特别意义了.
一定出现在这组数据中
探究新知
例5
一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示.你能根据表中的数据为这家鞋店提供进货建议吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
解:由上表看出,在鞋的尺码组成的数据中,23.5是这组数据的众数,
它的意义是:23.5cm的鞋销量最大.因此可以建议鞋店多进23.5cm的鞋.
例题讲解
1.
下面的扇形图描述了某种运动服的S号,M号,L号,XL号,XXL号在一家商场的销售情况.请你为这家商场提出进货建议.
解:由扇形图可以看出,在某种运动服大小型号组成的一组数据当中,M号最多为30%.因此可以建议这家商场多进M号的运动服.
针对练习
2.
某校男子足球队的年龄分布如下面条形图所示.请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
解:由图知13岁2人,14岁6人,15岁8人,16岁3人,17岁2人,18岁1人,一共22人.
所以足球队员年龄的平均数为:15岁;众数为:15岁;中位数为:15岁.
它们的含义分别是:校男子足球队员的平均年龄为15岁;校男子足球队员中年龄为15岁的队员最多;校男子足球队员的年龄不足15岁和超过15岁的人数相当.
1.一组数据的众数一定在这组数据中.
2.一组数据的众数可能不止一个.
3.众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
4.一组数据也可能没有众数,因为没有哪个数据出现的频数比哪个多.
归纳小结
1.学校团委组织八年级的共青团员参加植树活动,七个团支部植树棵数分别为16、13、15、16、14、17、17,则这组数据的中位数是
.
16
2.在一次女子体操比赛中,八名运动员的年龄(单位:岁)分别为:12、14、12、15、14、14、16、15,这组数据的众数是(
)
A.12
B.14
C.15
D.16
B
课堂练习
如图是连续十周测试甲、乙两名运动员体能训练成绩的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合格.
1.请根据图中所提供的信息填下表:
{5940675A-B579-460E-94D1-54222C63F5DA}
平均数
中位数
众数
体能测试成绩合格次数
甲
60
65
65
2
乙
60
57.5
80
4
2.请从不同的角度对运动员体能测试结果进行判断:
(1)根据平均数与成绩合格次数比较甲和乙,谁的成绩最好?
(2)根据平均数与中位数比较甲和乙,谁的成绩最好?
(3)根据折线统计图和成绩合格的次数,指出哪个的训练效果最好?
乙
乙
甲
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数据就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
中位数
众数
一组数据中出现次数最多的数据.
课堂小结
谢谢聆听
中位数与众数
第二十章
数据的分析
2021年春人教版八年级(下)数学
上节课我们学均数,知道它可以作为一组数据的代表,利用它可以反映一组数据的集中趋势.
除了平均数,还有什么样的数也可以来作为一组数据的代表,反映一组数据的集中趋势呢?
导入新课
1.理解中位数、众数的意义.
2.会利用样本的中位数去估计总体的中位数.
3.体会中位数和众数在统计中的作用.
重点:认识中位数、众数的意义,并会找一组数据的中位数和众数.
难点:利用中位数、众数分析数据信息做出决策.
学习目标
中位数
下表是某公司员工月收入的资料.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入/元
45000
18000
10000
5500
5000
3400
3000
1000
人数
1
1
1
3
6
1
11
1
(1)计算这个公司员工收入的平均数;
.
6276
问题2
探究新知
从上表可以看出平均数远远大于绝大多数人(22人)的实际月工资,绝大多数人“被平均”,不合适.
怎样准确的反映公司全体员工月收入水平?
(2)若用(1)算得的平均数反映公司全体员工月收入水平,你认为合适吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}月收入/元
45000
18000
10000
5500
5000
3400
3000
1000
人数
1
1
1
3
6
1
11
1
采用中位数
1.什么叫中位数?怎样确定一组数据的中位数?
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数据就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
不一定出现在这组数据中
一组数据的中位数是唯一的
探究新知
2.中位数反映的是一组数据的什么特征量?
反映了一组数据的集中趋势.
3.求下列数据的中位数.
(1)-2,0,-5,4,3,1;
(2)54,28,13,47.
答案:0.5
答案:37.5
分析:
将公司25名员工月收入数据由小到大排列,得到的中位数为3400,这说明除去月收入为3400元的员工,一半员工高于3400,另一半员工收入低于3400元。
例4
在一次男子马拉松长跑比赛中,抽得12名选手所用的时间(单位:min)如下:
136
140
129
180
124
154
146
145
158
175
165
148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142min,他的成绩如何?
例题讲解
解:(1)先将样本数据按照由小到大的顺序排列:
124
129
136
140
145
146
148
154
158
165
175
180
这组数据的中位数为处于中间的两个数146,148,即
因此样本数据的中位数是147.
(2)由(1)知样本数据的中位数为147,它的意义是:这次马拉松比赛中,大约有一半选手的成绩快于147min,有一半选手的成绩慢于147min.
这名选手的成绩是142min,快于中位数147min,因此可以推测他的成绩比一半以上选手的成绩好.
根据例4中的样本数据,你还有其他方法评价(2)中这名选手在这次比赛中的表现吗?
下面的条形图描述了某车间工人日加工零件数的情况.
请找出这些工人日加工零件数的中位数,并说明这个中位数的意义.
针对练习
解:由条形图知这组数据中从小到大排列为:4个3,5个4,8个5,9个6,6个7,4个8共36个数,则这组数据的中位数为处在中间两个数6,6的平均数,因此这些工人日加工零件的中位数为6.
这个中位数的意义:根据这个中位数,可以估计其车间工人日加工零件个数大于或小于这个数的人数各占一半.
众数
众数:一组数据中出现次数最多的数据.
众数反映了一组数据的集中趋势,当众数出现的次数越多,它就越能代表这组数据的整体状况.但当各数据重复出现的次数大致相等时,众数往往就没有什么特别意义了.
一定出现在这组数据中
探究新知
例5
一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示.你能根据表中的数据为这家鞋店提供进货建议吗?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
解:由上表看出,在鞋的尺码组成的数据中,23.5是这组数据的众数,
它的意义是:23.5cm的鞋销量最大.因此可以建议鞋店多进23.5cm的鞋.
例题讲解
1.
下面的扇形图描述了某种运动服的S号,M号,L号,XL号,XXL号在一家商场的销售情况.请你为这家商场提出进货建议.
解:由扇形图可以看出,在某种运动服大小型号组成的一组数据当中,M号最多为30%.因此可以建议这家商场多进M号的运动服.
针对练习
2.
某校男子足球队的年龄分布如下面条形图所示.请找出这些队员年龄的平均数、众数、中位数,并解释它们的意义.
解:由图知13岁2人,14岁6人,15岁8人,16岁3人,17岁2人,18岁1人,一共22人.
所以足球队员年龄的平均数为:15岁;众数为:15岁;中位数为:15岁.
它们的含义分别是:校男子足球队员的平均年龄为15岁;校男子足球队员中年龄为15岁的队员最多;校男子足球队员的年龄不足15岁和超过15岁的人数相当.
1.一组数据的众数一定在这组数据中.
2.一组数据的众数可能不止一个.
3.众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
4.一组数据也可能没有众数,因为没有哪个数据出现的频数比哪个多.
归纳小结
1.学校团委组织八年级的共青团员参加植树活动,七个团支部植树棵数分别为16、13、15、16、14、17、17,则这组数据的中位数是
.
16
2.在一次女子体操比赛中,八名运动员的年龄(单位:岁)分别为:12、14、12、15、14、14、16、15,这组数据的众数是(
)
A.12
B.14
C.15
D.16
B
课堂练习
如图是连续十周测试甲、乙两名运动员体能训练成绩的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合格.
1.请根据图中所提供的信息填下表:
{5940675A-B579-460E-94D1-54222C63F5DA}
平均数
中位数
众数
体能测试成绩合格次数
甲
60
65
65
2
乙
60
57.5
80
4
2.请从不同的角度对运动员体能测试结果进行判断:
(1)根据平均数与成绩合格次数比较甲和乙,谁的成绩最好?
(2)根据平均数与中位数比较甲和乙,谁的成绩最好?
(3)根据折线统计图和成绩合格的次数,指出哪个的训练效果最好?
乙
乙
甲
将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数据就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
中位数
众数
一组数据中出现次数最多的数据.
课堂小结
谢谢聆听
