2020-2021学年华东师大新版九年级下册数学期中复习试卷(Word版含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版九年级下册数学期中复习试卷(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 416.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 08:29:32 | ||
图片预览



文档简介
2020-2021学年华东师大新版九年级下册数学期中复习试卷
一.选择题(共10小题,满分40分,每小题4分)
1.8的立方根等于( )
A.﹣2
B.2
C.﹣4
D.4
2.下列计算中,正确的是( )
A.(2a)3=2a3
B.a3+a2=a5
C.a8÷a4=a2
D.(a2)3=a6
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
4.为了解某小区家庭使用垃圾袋的情况,小亮随机调查了该小区10户家庭一周垃圾袋的使用量,结果如下:7,9,11,8,7,14,10,8,9,7(单位:个),关于这组数据下列结论正确的是( )
A.方差是4
B.众数是7
C.中位数是8
D.平均数是10
5.如图,已知AE是⊙O的直径,∠B=40°,则∠CAE的度数为( )
A.40°
B.50°
C.60°
D.70°
6.如图,沿AC的方向开山修路,为了加快速度,要在小山的另一边同时施工,从AC上取一点B,取∠ABD=148°,已知BD=600米,∠D=58°,点A,C,E在同一直线上,那么开挖点E离点D的距离是( )
A.600sin58°米
B.600cos58°米
C.600tan58°米
D.米
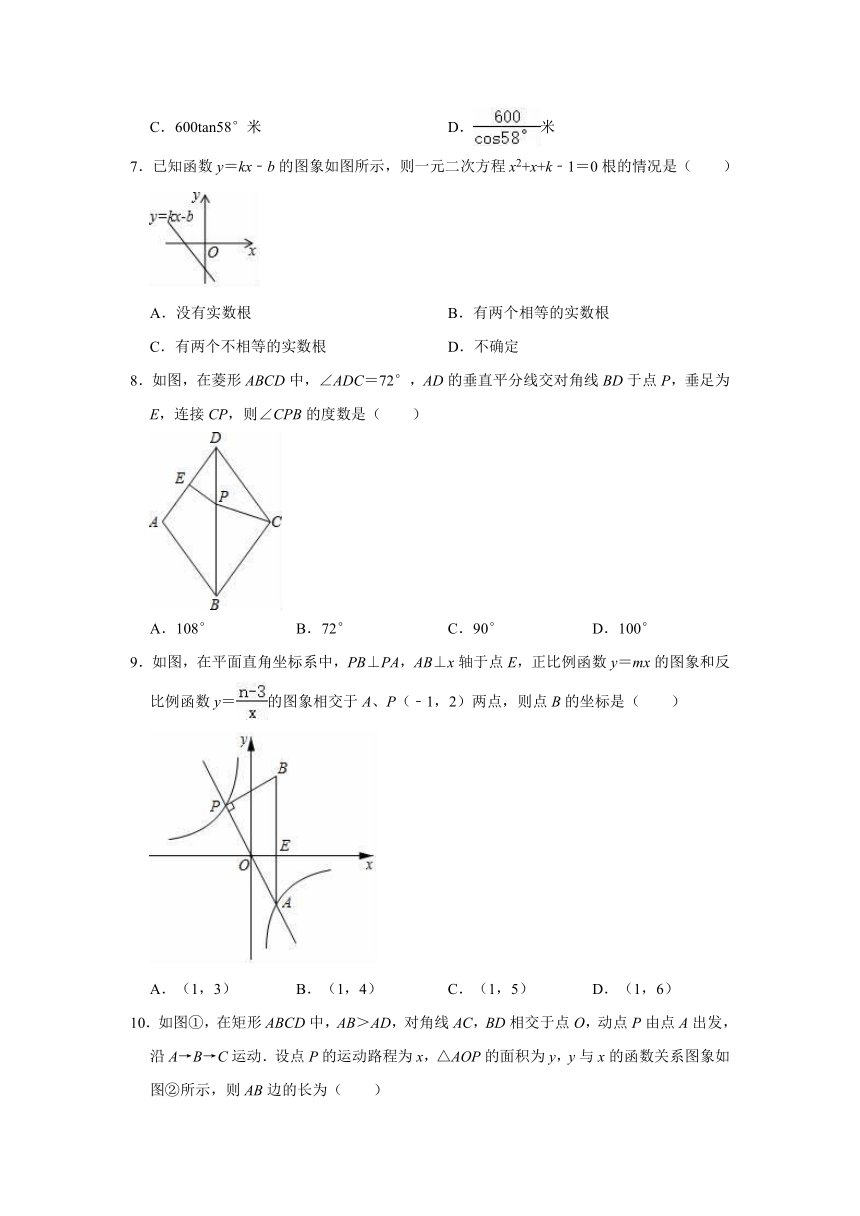
7.已知函数y=kx﹣b的图象如图所示,则一元二次方程x2+x+k﹣1=0根的情况是( )
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.不确定
8.如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )
A.108°
B.72°
C.90°
D.100°
9.如图,在平面直角坐标系中,PB⊥PA,AB⊥x轴于点E,正比例函数y=mx的图象和反比例函数y=的图象相交于A、P(﹣1,2)两点,则点B的坐标是( )
A.(1,3)
B.(1,4)
C.(1,5)
D.(1,6)
10.如图①,在矩形ABCD中,AB>AD,对角线AC,BD相交于点O,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AB边的长为( )
A.3
B.4
C.5
D.6
二.填空题(共6小题,满分24分,每小题4分)
11.我国最大的领海是南海,总面积有3500000km2,用科学记数法可表示为
km2.
12.若有意义,则x的取值范围是
.
13.若a、b互为相反数,c、d互为倒数,则的值为
.
14.已知一个凸多边形的每个内角都是150°,则它的边数为
.
15.已知矩形ABCD中,AB=2,AD=4,以AD为直径的半圆与BC相切于点,则图中阴影部分的面积为
(结果保留π)
16.如图,在Rt△ABC中,∠B=90°,AB=2,BC=1.将△ABC绕点A按逆时针方向旋转90°得到△AB'C',连接B'C,则tan∠ACB'=
.
三.解答题(共9小题,满分86分)
17.计算:6sin45°+|2﹣7|﹣()﹣3+(2020﹣)0.
18.先化简,再求值:(x﹣2+)÷,其中x=﹣.
19.已知:如图,AB=AE,AB∥DE,∠ECB+∠D=180°.
求证:△ABC≌△EAD.
20.如图,已知,在Rt△ABC中,∠ABC=90°,AB=1,AC=2.
(1)在线段BC找一点D,使得点D到边AC的距离等于DB的长(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求BD的长.
21.某一食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:g)
﹣5
﹣2
0
1
3
6
袋数
1
4
3
4
5
3
这批样品的平均质量比标准质量多还是少?多或少几克,若标准质量为450克,则抽样检测的总质量是多少?
22.已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
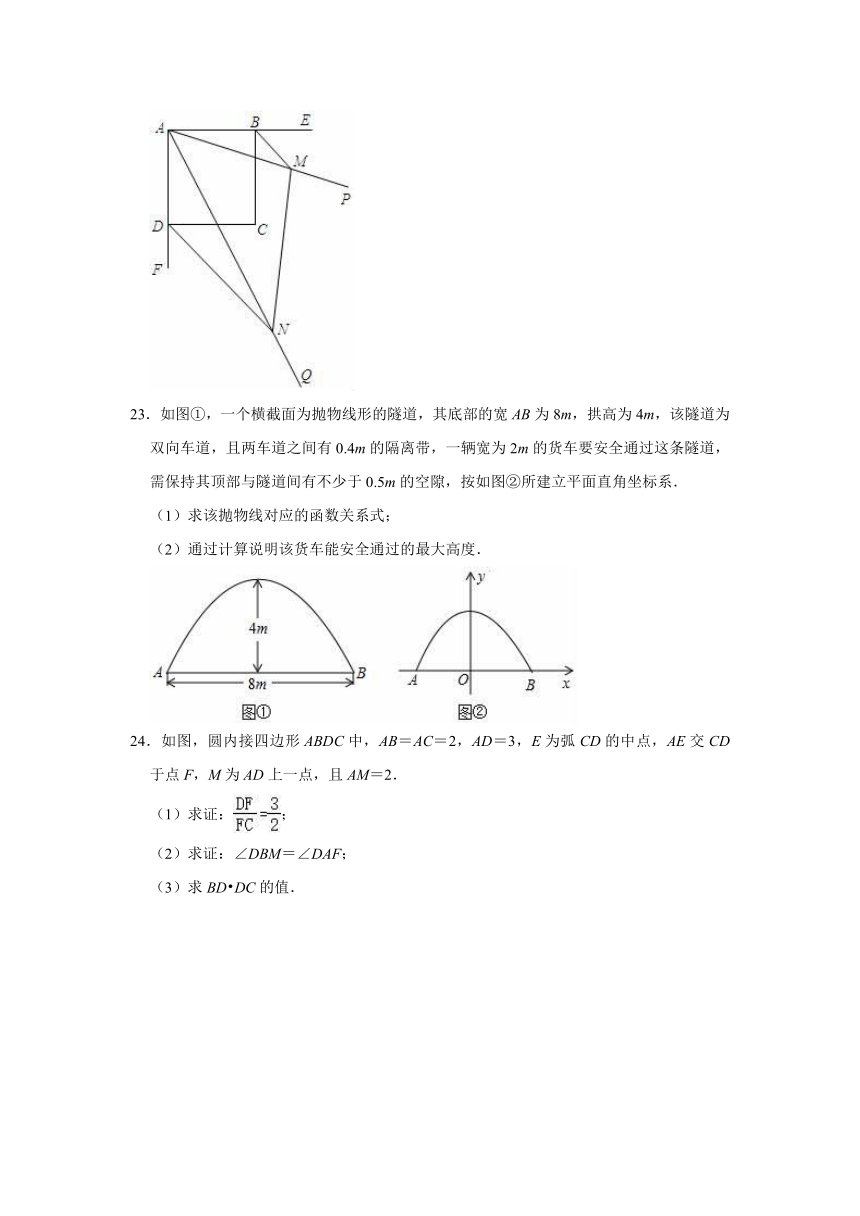
23.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8m,拱高为4m,该隧道为双向车道,且两车道之间有0.4m的隔离带,一辆宽为2m的货车要安全通过这条隧道,需保持其顶部与隧道间有不少于0.5m的空隙,按如图②所建立平面直角坐标系.
(1)求该抛物线对应的函数关系式;
(2)通过计算说明该货车能安全通过的最大高度.
24.如图,圆内接四边形ABDC中,AB=AC=2,AD=3,E为弧CD的中点,AE交CD于点F,M为AD上一点,且AM=2.
(1)求证:;
(2)求证:∠DBM=∠DAF;
(3)求BD?DC的值.
25.如图,抛物线y=ax2﹣3ax﹣2交x轴于A、B(A左B右)两点,交y轴于点C,过C作CD∥x轴,交抛物线于点D,E(﹣2,3)在抛物线上.
(1)求抛物线的解析式;
(2)P为第一象限抛物线上一点,过点P作PF⊥CD,垂足为F,连接PE交y轴于G,求证:FG∥DE;
(3)如图2,在(2)的条件下,过点F作FM⊥PE于M.若∠OFM=45°,求P点坐标.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:∵23=8,
∴8的立方根是2.
故选:B.
2.解:A、(2a)3=8a3,故本选项错误;
B、a3+a2不能合并,故本选项错误;
C、a8÷a4=a4,故本选项错误;
D、(a2)3=a6,故本选项正确;
故选:D.
3.解:A、是轴对称图形,又是中心对称图形,故此选项正确;
B、不是轴对称图形,不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
4.解:=(7+9+11+8+7+14+10+8+9+7)=9,
S2=
[(7﹣9)2+(9﹣9)2+(11﹣9)2+(8﹣9)2+(7﹣9)2+(14﹣9)2+(10﹣9)2+(8﹣9)2+(9﹣9)2+(7﹣9)2]=4.4,
众数是7,
中位数是=8.5,
故选:B.
5.解:∵AE是⊙O的直径,
∴∠ACE=90°,
∵∠B=∠E=40°,
∴∠CAE=90°﹣∠B=50°.
故选:B.
6.解:∵∠DBE=180°﹣∠ABD=180°﹣148°=32°,
∴∠E=180°﹣32°﹣58°=90°,
∴△BDE是直角三角形,
∵BD=600米,
∴开挖点E离点D的距离DE=600cos58°米.
故选:B.
7.解:由图象可得k<0,
∵△=12﹣4(k﹣1)=﹣4k+5,
而﹣4k>0,
∴△>0,
∴方程有两个不相等的实数根
故选:C.
8.解:连接PA,如图所示:
∵四边形ABCD是菱形,
∴∠ADP=∠CDP=∠ADC=36°,BD所在直线是菱形的对称轴,
∴PA=PC,
∵AD的垂直平分线交对角线BD于点P,
∴PA=PD,
∴PD=PC,
∴∠PCD=∠CDP=36°,
∴∠CPB=∠PCD+∠CDP=72°;
故选:B.
9.解:∵AP为正比例函数,故点A、P关于原点对称,则点A(1,﹣2),则设点B(1,t),
过点P作y轴的平行线交x轴于点N,交点B与x轴的平行线于点M,
∵∠MPB+∠NPO=90°,∠MPB+∠MBP=90°,
∴∠NPO=∠MPB,
BM=1﹣(﹣1)=2=PN=2,∠PNO=∠BMP=90°,
∴△PNO≌△BMP(AAS),
∴MP=ON=1,
故MN=MP+PN=1+2=3,
故点B的坐标为(1,3),
故选:A.
10.解:从图象看,当点P到达点B时,△AOP的面积为6,此时△AOP的高为BC,
∴△AOP的面积=×AB×(BC)=6,解得AB?BC=24①,
而从图②看,AB+BC=10②,
联立①②并解得,
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.解:将3500000用科学记数法表示为:3.5×106.
故答案为:3.5×106.
12.解:由题意得,x≥0且x﹣3≠0,
解得x≥0且x≠3.
故答案为:x≥0且x≠3.
13.解:根据题意得:a+b=0,cd=1,
则原式=0+3=3,
故答案为:3
14.解:∵一个凸多边形的每个内角都是150°,
∴对应的外角度数为180°﹣150°=30°,
∴多边形的边数是=12,
故答案为:12.
15.解:连接OE,如图所示:
∵以AD为直径的半圆O与BC相切于点E,
∴OD=2,OE⊥BC,
∵矩形ABCD中,AB=2,AD=4,
∴∠C=∠ADC=90°,CD=AB=2,
∴四边形OECD是矩形,OD=CD,
∴四边形OECD为正方形,
∴由弧DE、线段EC、CD所围成的面积=S正方形OECD﹣S扇形EOD=22﹣=4﹣π,
∵由弧DE、线段EC、CD所围成的面积=由弧AE、线段EB、AB所围成的面积,
∴阴影部分的面积=S△ABC﹣由弧AE、线段EB、AB所围成的面积=×2×4﹣(4﹣π)=π,
故答案为π.
16.解:在Rt△ABC中,由勾股定理得:AC===,
过C作CM⊥AB′于M,过A作AN⊥CB′于N,
∵根据旋转得出AB′=AB=2,∠B′AB=90°,
即∠CMA=∠MAB=∠B=90°,
∴CM=AB=2,AM=BC=1,
∴B′M=2﹣1=1,
在Rt△B′MC中,由勾股定理得:B′C===,
∴S△AB′C=B′C?AN=CM?AB′,
∴××AN=×2×2,
解得:AN=,
在Rt△ANC中,由勾股定理得:CN===,
∴tan∠ACB′===;
故答案为:.
三.解答题(共9小题,满分86分)
17.解:原式=6×+7﹣2﹣8+1,
=3+7﹣2﹣8+1,
=.
18.解:原式=(+)?
=?
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
19.证明:∵AB∥DE,
∴∠CAB=∠E,
∵∠ECB+∠D=180°,∠ECB+∠ACB=180°,
∴∠D=∠ACB,
在△ABC与△EAD中,
,
∴△ABC≌△EAD(AAS).
20.解:(1)如图,AD为所求.
(2)作DE⊥AC于E,如图,
∵∠ABC=90°,AB=1,AC=2.
∴在Rt△ABC中
∴BC===,
∵AD为角平分线,DB⊥AB,DE⊥AC,
∴BD=DE,
设BD=x,则DE=x,
∵S△ABD+S△ADC=S△ABC,
∴?AB?DB+?AC?DE=?AB?BC,
∴×1×x+×2×x=×1×,
∴x=,
即BD的长为.
21.解:与标准质量的差值的和为﹣5×1+(﹣2)×4+0×3+1×4+3×5+6×3=24,其平均数为24÷20=1.2,即这批样品的平均质量比标准质量多,多1.2克.
则抽样检测的总质量是(450+1.2)×20=9024(克).
22.(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,
∵BM、DN分别是正方形的两个外角平分线,
∴∠ABM=∠ADN=135°,
∵∠MAN=45°,
∴∠BAM=∠AND=45°﹣∠DAN,
∴△ABM∽△NDA;
(2)解:当∠BAM=22.5°时,四边形BMND为矩形;理由如下:
∵∠BAM=22.5°,∠EBM=45°,
∴∠AMB=22.5°,
∴∠BAM=∠AMB,
∴AB=BM,
同理AD=DN,
∵AB=AD,∴BM=DN,
∵四边形ABCD是正方形
∴∠ABD=∠ADB=45°,
∴∠BDN=∠DBM=90°
∴∠BDN+∠DBM=180°,
∴BM∥DN
∴四边形BMND为平行四边形,
∵∠BDN=90°,
∴四边形BMND为矩形.
23.解:(1)如图②中,A(4,0),C(0,4),
设抛物线解析式为y=ax2+k,
由题意,得,
解得:,
∴抛物线表达式为.
(2)2+=2.2,
当x=2.2时,y=﹣×2.22+4=2.79,
当y=2.79时,2.79﹣0.5=2.29
(m).
答:该货车能够通行的最大高度为2.29
m.
24.证明:(1)过点D作DH∥AC交AE的延长线于H,
∵E为弧CD的中点,
∴=,
∴∠DAE=∠CAE,
∵DH∥AC,
∴∠H=∠CAF,
∴∠DAE=∠H,
∴DA=DH=3,
∵AC∥DH,
∴=;
(2)∵AB=AC=2,
∴=,
∴∠ADB=∠ADC,
∵∠ADC+∠C+∠DAC=180°,
∴∠ADC=180°﹣∠C﹣2∠DAF,
∵AB=AM=2,
∴∠ABM=∠AMB,
∵∠AMB=∠ADB+∠DBM,
∴∠ABM=∠ADB+∠DBM,
∴∠ABD=2∠DBM+∠ADB,
∵四边形ABDC是圆内接四边形,
∴∠C+∠ABD=180°,
∴∠C+2∠DBM+∠ADB=180°,
∴∠ADB=180°﹣∠C﹣2∠DBM,
∴∠DAF=∠DBM;
(3)∵,
∴DF=DC,
∵∠DAF=∠DBM,∠ADB=∠ADC,
∴△BDM∽△ADF,
∴,
∴,
∴BD?DC=5.
25.解:(1)∵E(﹣2,3)在抛物线y=ax2﹣3ax﹣2上,
∴4a+6a﹣2=3,
解得:a=,
∴抛物线解析式为y=x2﹣x﹣2.
(2)证明:∵y=x2﹣x﹣2=0时,解得:x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
∵x=0时,y=x2﹣x﹣2=﹣2,
∴C(0,﹣2),
∵点D在抛物线上,且CD∥x轴,
∴D(3,﹣2),
设直线DE解析式为y=kx+b
∴
解得:,
∴直线DE:y=﹣x+1,
∵点P为第一象限抛物线上一点,
∴设点P坐标为(t,
t2﹣t﹣2)(t>4),
设直线PE解析式为y=cx+d,
∴
解得:,
∴直线PE:y=x+t﹣2,直线PE与y轴交点G(0,t﹣2),
∵PF⊥CD于点F,
∴F(t,﹣2),
设直线FG解析式为y=ex+t﹣2,
把点F代入得:te+t﹣2=﹣2,
解得:e=﹣1,
∴FG∥DE,
(3)延长FO、PE相交于点N,过点M作MG′⊥PF于点G′,过点N作NH⊥MG′交G′M的延长线于点H,
∴∠FG′M=∠MHN=90°,
∵FM⊥PE于M,
∴∠FMN=90°,
∴∠FMG′+∠NMH=∠MNH+∠NMH=90°,
∴∠FMG′=∠MNH,
∵∠OFM=45°,
∴∠MNF=180°﹣∠FMN﹣∠OFM=45°,
∴FM=MN,
在△FG′M与△MHN中
,
∴△FG′M≌△MHN(AAS),
∴FG′=MH,MG′=NH,
∵F(t,﹣2),
∴直线OF:y=﹣x,
∵点M在直线PE:y=x+t﹣2上,
∴设M(m,
m+t﹣2),
∴MG′=t﹣m,FG′=m+t﹣2﹣(﹣2)=m+t,
∵
解得:,
∴N(,),
∴MH=m﹣,NH=m+t﹣2﹣,
∴,
解得:
(舍去),
∴yP=×36﹣×6﹣2=7,
∴点P坐标为(6,7).
解法二:过点G作GH⊥PF于H,交FM于N,连接ON,设P(a,
a2﹣a﹣2),设NH=b,
由△GHP≌△FHN,推出NH=PH=b,
证明ON=OC+NH=b+2,
在Rt△OGN中,则有(b+2)2=(a﹣2)2+(a﹣b)2,
∴b=,
又b=PH=a(a﹣5),
∴=,
∴a2﹣5a﹣6=0,
∴a=6或﹣1(舍弃),
∴P(6,7).
一.选择题(共10小题,满分40分,每小题4分)
1.8的立方根等于( )
A.﹣2
B.2
C.﹣4
D.4
2.下列计算中,正确的是( )
A.(2a)3=2a3
B.a3+a2=a5
C.a8÷a4=a2
D.(a2)3=a6
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
4.为了解某小区家庭使用垃圾袋的情况,小亮随机调查了该小区10户家庭一周垃圾袋的使用量,结果如下:7,9,11,8,7,14,10,8,9,7(单位:个),关于这组数据下列结论正确的是( )
A.方差是4
B.众数是7
C.中位数是8
D.平均数是10
5.如图,已知AE是⊙O的直径,∠B=40°,则∠CAE的度数为( )
A.40°
B.50°
C.60°
D.70°
6.如图,沿AC的方向开山修路,为了加快速度,要在小山的另一边同时施工,从AC上取一点B,取∠ABD=148°,已知BD=600米,∠D=58°,点A,C,E在同一直线上,那么开挖点E离点D的距离是( )
A.600sin58°米
B.600cos58°米
C.600tan58°米
D.米
7.已知函数y=kx﹣b的图象如图所示,则一元二次方程x2+x+k﹣1=0根的情况是( )
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.不确定
8.如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是( )
A.108°
B.72°
C.90°
D.100°
9.如图,在平面直角坐标系中,PB⊥PA,AB⊥x轴于点E,正比例函数y=mx的图象和反比例函数y=的图象相交于A、P(﹣1,2)两点,则点B的坐标是( )
A.(1,3)
B.(1,4)
C.(1,5)
D.(1,6)
10.如图①,在矩形ABCD中,AB>AD,对角线AC,BD相交于点O,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AB边的长为( )
A.3
B.4
C.5
D.6
二.填空题(共6小题,满分24分,每小题4分)
11.我国最大的领海是南海,总面积有3500000km2,用科学记数法可表示为
km2.
12.若有意义,则x的取值范围是
.
13.若a、b互为相反数,c、d互为倒数,则的值为
.
14.已知一个凸多边形的每个内角都是150°,则它的边数为
.
15.已知矩形ABCD中,AB=2,AD=4,以AD为直径的半圆与BC相切于点,则图中阴影部分的面积为
(结果保留π)
16.如图,在Rt△ABC中,∠B=90°,AB=2,BC=1.将△ABC绕点A按逆时针方向旋转90°得到△AB'C',连接B'C,则tan∠ACB'=
.
三.解答题(共9小题,满分86分)
17.计算:6sin45°+|2﹣7|﹣()﹣3+(2020﹣)0.
18.先化简,再求值:(x﹣2+)÷,其中x=﹣.
19.已知:如图,AB=AE,AB∥DE,∠ECB+∠D=180°.
求证:△ABC≌△EAD.
20.如图,已知,在Rt△ABC中,∠ABC=90°,AB=1,AC=2.
(1)在线段BC找一点D,使得点D到边AC的距离等于DB的长(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,求BD的长.
21.某一食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:g)
﹣5
﹣2
0
1
3
6
袋数
1
4
3
4
5
3
这批样品的平均质量比标准质量多还是少?多或少几克,若标准质量为450克,则抽样检测的总质量是多少?
22.已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
(1)求证:△ABM∽△NDA;
(2)连接BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
23.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8m,拱高为4m,该隧道为双向车道,且两车道之间有0.4m的隔离带,一辆宽为2m的货车要安全通过这条隧道,需保持其顶部与隧道间有不少于0.5m的空隙,按如图②所建立平面直角坐标系.
(1)求该抛物线对应的函数关系式;
(2)通过计算说明该货车能安全通过的最大高度.
24.如图,圆内接四边形ABDC中,AB=AC=2,AD=3,E为弧CD的中点,AE交CD于点F,M为AD上一点,且AM=2.
(1)求证:;
(2)求证:∠DBM=∠DAF;
(3)求BD?DC的值.
25.如图,抛物线y=ax2﹣3ax﹣2交x轴于A、B(A左B右)两点,交y轴于点C,过C作CD∥x轴,交抛物线于点D,E(﹣2,3)在抛物线上.
(1)求抛物线的解析式;
(2)P为第一象限抛物线上一点,过点P作PF⊥CD,垂足为F,连接PE交y轴于G,求证:FG∥DE;
(3)如图2,在(2)的条件下,过点F作FM⊥PE于M.若∠OFM=45°,求P点坐标.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:∵23=8,
∴8的立方根是2.
故选:B.
2.解:A、(2a)3=8a3,故本选项错误;
B、a3+a2不能合并,故本选项错误;
C、a8÷a4=a4,故本选项错误;
D、(a2)3=a6,故本选项正确;
故选:D.
3.解:A、是轴对称图形,又是中心对称图形,故此选项正确;
B、不是轴对称图形,不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、不是轴对称图形,是中心对称图形,故此选项错误;
故选:A.
4.解:=(7+9+11+8+7+14+10+8+9+7)=9,
S2=
[(7﹣9)2+(9﹣9)2+(11﹣9)2+(8﹣9)2+(7﹣9)2+(14﹣9)2+(10﹣9)2+(8﹣9)2+(9﹣9)2+(7﹣9)2]=4.4,
众数是7,
中位数是=8.5,
故选:B.
5.解:∵AE是⊙O的直径,
∴∠ACE=90°,
∵∠B=∠E=40°,
∴∠CAE=90°﹣∠B=50°.
故选:B.
6.解:∵∠DBE=180°﹣∠ABD=180°﹣148°=32°,
∴∠E=180°﹣32°﹣58°=90°,
∴△BDE是直角三角形,
∵BD=600米,
∴开挖点E离点D的距离DE=600cos58°米.
故选:B.
7.解:由图象可得k<0,
∵△=12﹣4(k﹣1)=﹣4k+5,
而﹣4k>0,
∴△>0,
∴方程有两个不相等的实数根
故选:C.
8.解:连接PA,如图所示:
∵四边形ABCD是菱形,
∴∠ADP=∠CDP=∠ADC=36°,BD所在直线是菱形的对称轴,
∴PA=PC,
∵AD的垂直平分线交对角线BD于点P,
∴PA=PD,
∴PD=PC,
∴∠PCD=∠CDP=36°,
∴∠CPB=∠PCD+∠CDP=72°;
故选:B.
9.解:∵AP为正比例函数,故点A、P关于原点对称,则点A(1,﹣2),则设点B(1,t),
过点P作y轴的平行线交x轴于点N,交点B与x轴的平行线于点M,
∵∠MPB+∠NPO=90°,∠MPB+∠MBP=90°,
∴∠NPO=∠MPB,
BM=1﹣(﹣1)=2=PN=2,∠PNO=∠BMP=90°,
∴△PNO≌△BMP(AAS),
∴MP=ON=1,
故MN=MP+PN=1+2=3,
故点B的坐标为(1,3),
故选:A.
10.解:从图象看,当点P到达点B时,△AOP的面积为6,此时△AOP的高为BC,
∴△AOP的面积=×AB×(BC)=6,解得AB?BC=24①,
而从图②看,AB+BC=10②,
联立①②并解得,
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.解:将3500000用科学记数法表示为:3.5×106.
故答案为:3.5×106.
12.解:由题意得,x≥0且x﹣3≠0,
解得x≥0且x≠3.
故答案为:x≥0且x≠3.
13.解:根据题意得:a+b=0,cd=1,
则原式=0+3=3,
故答案为:3
14.解:∵一个凸多边形的每个内角都是150°,
∴对应的外角度数为180°﹣150°=30°,
∴多边形的边数是=12,
故答案为:12.
15.解:连接OE,如图所示:
∵以AD为直径的半圆O与BC相切于点E,
∴OD=2,OE⊥BC,
∵矩形ABCD中,AB=2,AD=4,
∴∠C=∠ADC=90°,CD=AB=2,
∴四边形OECD是矩形,OD=CD,
∴四边形OECD为正方形,
∴由弧DE、线段EC、CD所围成的面积=S正方形OECD﹣S扇形EOD=22﹣=4﹣π,
∵由弧DE、线段EC、CD所围成的面积=由弧AE、线段EB、AB所围成的面积,
∴阴影部分的面积=S△ABC﹣由弧AE、线段EB、AB所围成的面积=×2×4﹣(4﹣π)=π,
故答案为π.
16.解:在Rt△ABC中,由勾股定理得:AC===,
过C作CM⊥AB′于M,过A作AN⊥CB′于N,
∵根据旋转得出AB′=AB=2,∠B′AB=90°,
即∠CMA=∠MAB=∠B=90°,
∴CM=AB=2,AM=BC=1,
∴B′M=2﹣1=1,
在Rt△B′MC中,由勾股定理得:B′C===,
∴S△AB′C=B′C?AN=CM?AB′,
∴××AN=×2×2,
解得:AN=,
在Rt△ANC中,由勾股定理得:CN===,
∴tan∠ACB′===;
故答案为:.
三.解答题(共9小题,满分86分)
17.解:原式=6×+7﹣2﹣8+1,
=3+7﹣2﹣8+1,
=.
18.解:原式=(+)?
=?
=2(x+2)
=2x+4,
当x=﹣时,
原式=2×(﹣)+4
=﹣1+4
=3.
19.证明:∵AB∥DE,
∴∠CAB=∠E,
∵∠ECB+∠D=180°,∠ECB+∠ACB=180°,
∴∠D=∠ACB,
在△ABC与△EAD中,
,
∴△ABC≌△EAD(AAS).
20.解:(1)如图,AD为所求.
(2)作DE⊥AC于E,如图,
∵∠ABC=90°,AB=1,AC=2.
∴在Rt△ABC中
∴BC===,
∵AD为角平分线,DB⊥AB,DE⊥AC,
∴BD=DE,
设BD=x,则DE=x,
∵S△ABD+S△ADC=S△ABC,
∴?AB?DB+?AC?DE=?AB?BC,
∴×1×x+×2×x=×1×,
∴x=,
即BD的长为.
21.解:与标准质量的差值的和为﹣5×1+(﹣2)×4+0×3+1×4+3×5+6×3=24,其平均数为24÷20=1.2,即这批样品的平均质量比标准质量多,多1.2克.
则抽样检测的总质量是(450+1.2)×20=9024(克).
22.(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠ADC=∠BAD=90°,
∵BM、DN分别是正方形的两个外角平分线,
∴∠ABM=∠ADN=135°,
∵∠MAN=45°,
∴∠BAM=∠AND=45°﹣∠DAN,
∴△ABM∽△NDA;
(2)解:当∠BAM=22.5°时,四边形BMND为矩形;理由如下:
∵∠BAM=22.5°,∠EBM=45°,
∴∠AMB=22.5°,
∴∠BAM=∠AMB,
∴AB=BM,
同理AD=DN,
∵AB=AD,∴BM=DN,
∵四边形ABCD是正方形
∴∠ABD=∠ADB=45°,
∴∠BDN=∠DBM=90°
∴∠BDN+∠DBM=180°,
∴BM∥DN
∴四边形BMND为平行四边形,
∵∠BDN=90°,
∴四边形BMND为矩形.
23.解:(1)如图②中,A(4,0),C(0,4),
设抛物线解析式为y=ax2+k,
由题意,得,
解得:,
∴抛物线表达式为.
(2)2+=2.2,
当x=2.2时,y=﹣×2.22+4=2.79,
当y=2.79时,2.79﹣0.5=2.29
(m).
答:该货车能够通行的最大高度为2.29
m.
24.证明:(1)过点D作DH∥AC交AE的延长线于H,
∵E为弧CD的中点,
∴=,
∴∠DAE=∠CAE,
∵DH∥AC,
∴∠H=∠CAF,
∴∠DAE=∠H,
∴DA=DH=3,
∵AC∥DH,
∴=;
(2)∵AB=AC=2,
∴=,
∴∠ADB=∠ADC,
∵∠ADC+∠C+∠DAC=180°,
∴∠ADC=180°﹣∠C﹣2∠DAF,
∵AB=AM=2,
∴∠ABM=∠AMB,
∵∠AMB=∠ADB+∠DBM,
∴∠ABM=∠ADB+∠DBM,
∴∠ABD=2∠DBM+∠ADB,
∵四边形ABDC是圆内接四边形,
∴∠C+∠ABD=180°,
∴∠C+2∠DBM+∠ADB=180°,
∴∠ADB=180°﹣∠C﹣2∠DBM,
∴∠DAF=∠DBM;
(3)∵,
∴DF=DC,
∵∠DAF=∠DBM,∠ADB=∠ADC,
∴△BDM∽△ADF,
∴,
∴,
∴BD?DC=5.
25.解:(1)∵E(﹣2,3)在抛物线y=ax2﹣3ax﹣2上,
∴4a+6a﹣2=3,
解得:a=,
∴抛物线解析式为y=x2﹣x﹣2.
(2)证明:∵y=x2﹣x﹣2=0时,解得:x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
∵x=0时,y=x2﹣x﹣2=﹣2,
∴C(0,﹣2),
∵点D在抛物线上,且CD∥x轴,
∴D(3,﹣2),
设直线DE解析式为y=kx+b
∴
解得:,
∴直线DE:y=﹣x+1,
∵点P为第一象限抛物线上一点,
∴设点P坐标为(t,
t2﹣t﹣2)(t>4),
设直线PE解析式为y=cx+d,
∴
解得:,
∴直线PE:y=x+t﹣2,直线PE与y轴交点G(0,t﹣2),
∵PF⊥CD于点F,
∴F(t,﹣2),
设直线FG解析式为y=ex+t﹣2,
把点F代入得:te+t﹣2=﹣2,
解得:e=﹣1,
∴FG∥DE,
(3)延长FO、PE相交于点N,过点M作MG′⊥PF于点G′,过点N作NH⊥MG′交G′M的延长线于点H,
∴∠FG′M=∠MHN=90°,
∵FM⊥PE于M,
∴∠FMN=90°,
∴∠FMG′+∠NMH=∠MNH+∠NMH=90°,
∴∠FMG′=∠MNH,
∵∠OFM=45°,
∴∠MNF=180°﹣∠FMN﹣∠OFM=45°,
∴FM=MN,
在△FG′M与△MHN中
,
∴△FG′M≌△MHN(AAS),
∴FG′=MH,MG′=NH,
∵F(t,﹣2),
∴直线OF:y=﹣x,
∵点M在直线PE:y=x+t﹣2上,
∴设M(m,
m+t﹣2),
∴MG′=t﹣m,FG′=m+t﹣2﹣(﹣2)=m+t,
∵
解得:,
∴N(,),
∴MH=m﹣,NH=m+t﹣2﹣,
∴,
解得:
(舍去),
∴yP=×36﹣×6﹣2=7,
∴点P坐标为(6,7).
解法二:过点G作GH⊥PF于H,交FM于N,连接ON,设P(a,
a2﹣a﹣2),设NH=b,
由△GHP≌△FHN,推出NH=PH=b,
证明ON=OC+NH=b+2,
在Rt△OGN中,则有(b+2)2=(a﹣2)2+(a﹣b)2,
∴b=,
又b=PH=a(a﹣5),
∴=,
∴a2﹣5a﹣6=0,
∴a=6或﹣1(舍弃),
∴P(6,7).
同课章节目录
