24.1.4圆周角

(共18张PPT)
23.1圆周角
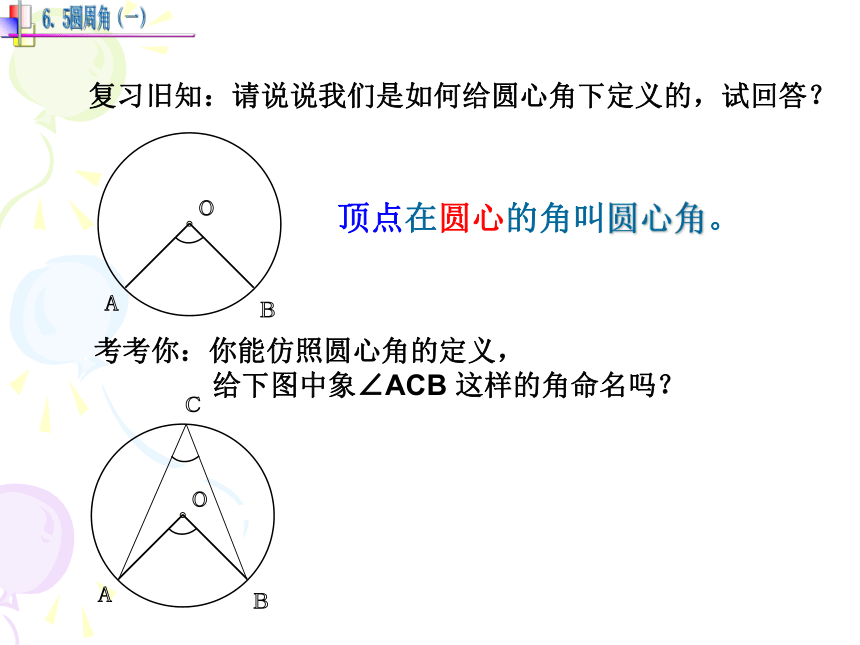
复习旧知：请说说我们是如何给圆心角下定义的，试回答？
顶点在圆心的角叫圆心角。
考考你：你能仿照圆心角的定义，
给下图中象∠ACB 这样的角命名吗？
1.理解圆周角的概念
2.掌握圆周角定理
学习目标
学法指导
认真自学课本84—86页“定理”，会解决下列问题：
1.什么是圆周角 它与圆心角有什么区别
2.完成“探究”，写出你发现的规律。
3.如何证明“同弧所对的圆周角等于该弧所对的
圆心角的一半” 需要分情况吗
4.如何证明“同弧或等弧所对的圆周角相等”
(时间:8分钟)
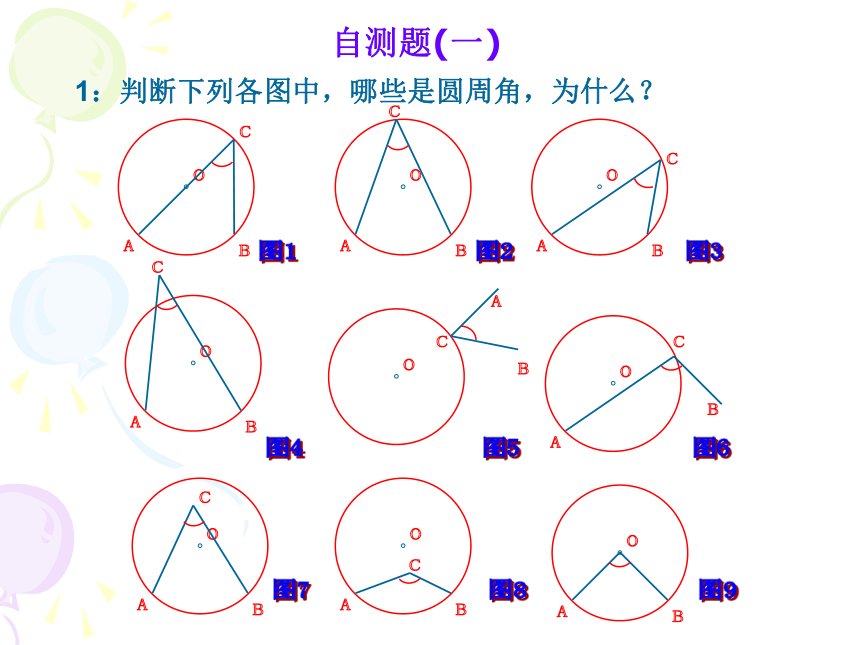
1：判断下列各图中，哪些是圆周角，为什么？
自测题(一)
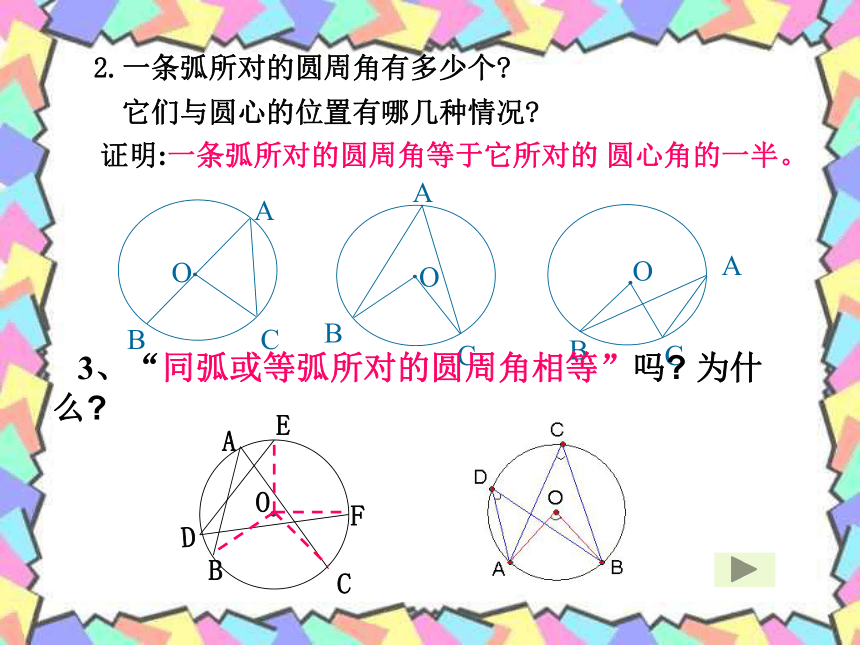
2.一条弧所对的圆周角有多少个
它们与圆心的位置有哪几种情况
证明:一条弧所对的圆周角等于它所对的 圆心角的一半。
O
A
B
C
O
A
B
C
O
A
B
C
3、“同弧或等弧所对的圆周角相等”吗 为什么
O
C
B
A
F
E
D
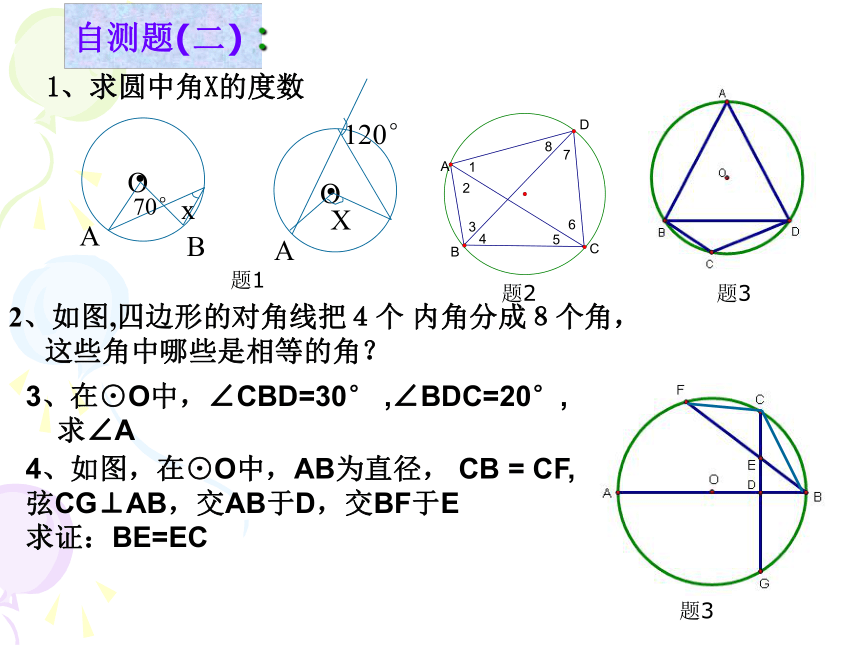
自测题(二) :
3、在⊙O中，∠CBD=30° ,∠BDC=20°,
求∠A
4、如图，在⊙O中，AB为直径， CB = CF,
弦CG⊥AB，交AB于D，交BF于E
求证：BE=EC
1、求圆中角X的度数
A
B
A
O
.
70°
x
O
.
X
120°
题1
题3
题2
2、如图,四边形的对角线把４个 内角分成８个角，
这些角中哪些是相等的角？
题3
1.圆周角定义:
顶点在圆上,并且两边都和圆相交的角 叫圆周角。
2.圆周角定理：
在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
小结:
作业:
1、课本94页第4、11题
分三种情况来证明：
（1）圆心在∠BAC的一边上.
A
O
B
C
1
2
证明:∵ OA=OC
∴ ∠C=∠BAC
∵∠BOC=∠BAC+∠C
∴ ∠BAC= ∠BOC
（2）圆心在∠BAC的内部.
O
A
B
C
D
1
2
1
2
证明:作直径AD.
∵∠BAD= ∠BOD
∠DAC= ∠DOC
∵∠BAD+∠DAC= （∠ BOD+∠DOC）
即: ∠BAC= ∠BOC
1
2
1
2
（3）圆心在∠BAC的外部.
A
B
O
C
D
证明:作直径AD.
∵∠DAB= ∠DOB
∠DAC= ∠DOC
∴ ∠DAC-∠DAB= （∠DOC-∠DOB）
即: ∠BAC= ∠BOC
1
2
1
2
1
2
1
2
探索（一）
1、如图，点C是⊙O上任意一点（除点A、B），
（１）若弦AB是⊙O的直径，
则圆周角∠ACB会是怎样的角？
（２）90°的圆周角所对的弦是什么
由此你能发现的结论是什么呢？
O
C
B
A
半圆（或直径）所对的圆周角是直角，
90°的圆周角所对的弦是直径
D
C
B
A
O
E
2、四边形ABCD是圆内接四边形吗？
∠A+∠C=1800吗？ 为什么？
∠B+∠D=1800呢？
圆内接四边形的对角互补，
外角等于它的内对角。
探索（二）
3.如图，若圆周角∠ＢＡＣ与∠ＥＤＦ相等，
则ＢＣ与ＥＦ相等吗？为什么？
由此你能发现的结论是什么呢？
O
C
B
A
在同圆或等圆中，相等的圆周角所对的弧相等，
O
C
B
A
F
E
D
如果三角形一边上的中线等于这边的一半，
那么这个三角形是直角三角形
4．如图，⊿ＡＢＣ中，ＯＣ是ＡＢ边的中线，
　　ＯC＝ ＡＢ， 则 ⊿ＡＢＣ是直角三角形吗？
　　由此你能发现的结论是什么呢？
︵
︵
1
2
例题评析
如图, ⊙O的直径 AB 为10 cm，弦 AC 为６cm,
∠ACB 的平分线交⊙O于 D, 求BC、AD、BD的长.
　　　　　　　练一练
1、在⊙O中，一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°，则x=_ _；
２、⊙O的弦AB长等于圆的半径，求该弦所对的圆心角和圆周角的度数。
３、AB、AC为⊙O的两条弦，延长CA到D，使 AD=AB，如果∠ADB=35° ，求∠BOC的度数。４、如图：0A、OB、OC都是⊙O的半径，∠AOB=2∠BOC。求证： ∠ACB=2 ∠BAC。
作业:
1、课本94页第题