24.2.2直线和圆的位置关系(2)
文档属性
| 名称 | 24.2.2直线和圆的位置关系(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 771.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-02 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
24.2.2 圆的切线的判定与性质
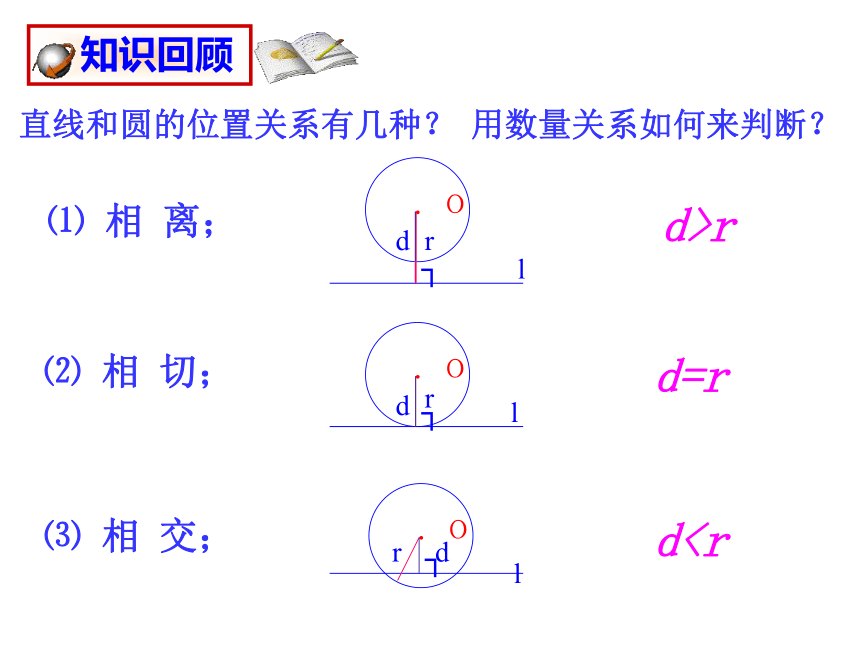
直线和圆的位置关系有几种?
知识回顾
⑴ 相 离;
⑵ 相 切;
⑶ 相 交;
dd=r
d>r
用数量关系如何来判断?
.O
l
┐
d
r
.O
l
┐
d
r
.O
l
┐
d
r
观察与思考
问题1:下雨天,转动的雨伞上的水滴是
顺着伞的什么方向飞出去的
问题2:砂轮转动时,火花是沿着砂轮的
什么方向飞出去的
学习目标
1、理解圆的切线的判定与性质定理。
2、掌握判定直线是圆的切线的思路方法。
3、理解与切线有关的添加辅助线的方法。
认真阅读课本95-96页,完成下列自学任务:
1、完成P95“思考”:切线的判定定理是什么?
说出题设和结论,会用符号表示出来。
2、尝试完成“例1”:如何添加辅助线?
判定一条直线是圆的切线的证明思路是什么?
3、完成P96“思考”:切线的性质定理是什么?
说出题设和结论,你能用反证法证明吗?
学法指导
(若有困难,同伴交流) 时间:8分钟
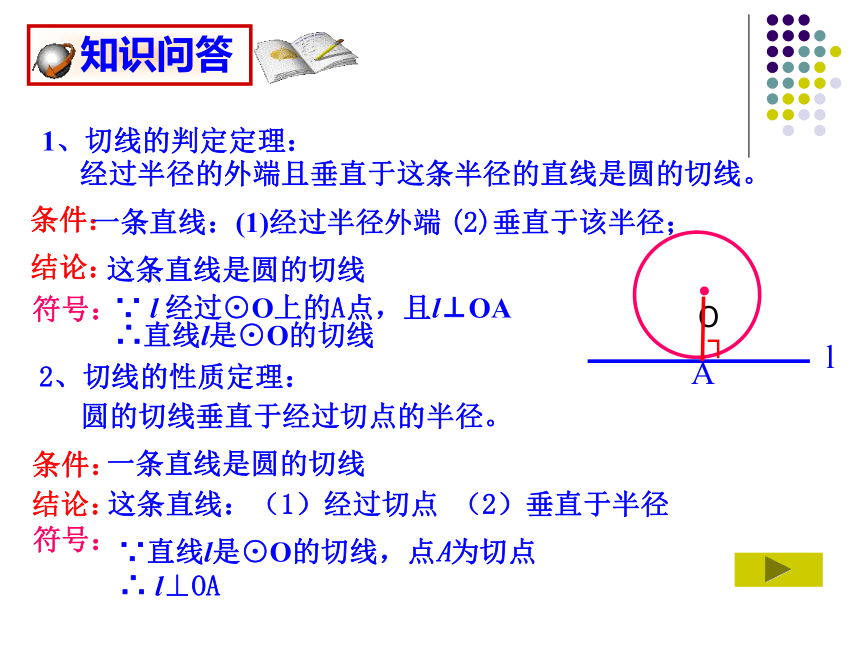
1、切线的判定定理:
条件:
一条直线:(1)经过半径外端 (2)垂直于该半径;
∵直线l是⊙O的切线,点A为切点
知识问答
●O
┐
A
l
符号:
圆的切线垂直于经过切点的半径。
∴ l⊥OA
∵ l 经过⊙O上的A点,且l⊥OA
∴直线l是⊙O的切线
条件:
符号:
结论:
结论:
这条直线是圆的切线
一条直线是圆的切线
这条直线:(1)经过切点 (2)垂直于半径
经过半径的外端且垂直于这条半径的直线是圆的切线。
2、切线的性质定理:
例1、如右图所示,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解:直线AB是⊙O的切线 。理由如下:
例题欣赏
∵AB=OA,∠OBA=45°(已知)
∴∠AOB=∠OBA=45°(等边对等角)
∴∠OAB=180°-∠OBA-∠AOB=90°
∴ 直线AB⊥OA
∴直线AB是⊙O的切线
A
B
O
●
自我检测
1、判断题:
2、以三角形的一边为直径的圆恰好与另一边相切,则此三角 形是__________三角形
直角
×
(1) 垂直于圆的半径的直线一定是这个圆的切线。 ( )
(2) 过圆的半径的外端的直线一定是这个圆的切线 。( )
×
4、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
O
●
A
B
C
D
3、课本96页 :练习1、2
5、如右图所示,已知OC平分∠AOB,D是OC上任意一点,⊙D与OA相切于点E。那么,OB是⊙D的切线吗?请说明理由。
E
C
D
●
A
B
O
F
┐
在本节的学习中:
你的收获是 ;
你的疑问是 。
谈一谈
1、如何判定一条直线是已知圆的切线?
(1)只有一个公共点;
(2) d=r
(3)过半径外端且垂直于这条半径的直线是圆的切线;
2、圆的切线有什么性质?
(3)圆的切线垂直于经过切点的半径。
(1)只有一个公共点;
(2) d=r
3、解决切线问题时如何添加辅助线呢?
(1)若直线与圆公共点明确时: 连半径证垂直;
(2)若直线与圆公共点不确定时:作垂线证半径。
(3)若直线和圆相切于某个点时:连半径得垂直。
作业:
课本101至111页 : 4、14 题
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上反例可以看出,只满足其中一个条件的直线不是圆的切线.必需同时满足,二者缺一不可
切线的判定定理
24.2.2 圆的切线的判定与性质
直线和圆的位置关系有几种?
知识回顾
⑴ 相 离;
⑵ 相 切;
⑶ 相 交;
d
d>r
用数量关系如何来判断?
.O
l
┐
d
r
.O
l
┐
d
r
.O
l
┐
d
r
观察与思考
问题1:下雨天,转动的雨伞上的水滴是
顺着伞的什么方向飞出去的
问题2:砂轮转动时,火花是沿着砂轮的
什么方向飞出去的
学习目标
1、理解圆的切线的判定与性质定理。
2、掌握判定直线是圆的切线的思路方法。
3、理解与切线有关的添加辅助线的方法。
认真阅读课本95-96页,完成下列自学任务:
1、完成P95“思考”:切线的判定定理是什么?
说出题设和结论,会用符号表示出来。
2、尝试完成“例1”:如何添加辅助线?
判定一条直线是圆的切线的证明思路是什么?
3、完成P96“思考”:切线的性质定理是什么?
说出题设和结论,你能用反证法证明吗?
学法指导
(若有困难,同伴交流) 时间:8分钟
1、切线的判定定理:
条件:
一条直线:(1)经过半径外端 (2)垂直于该半径;
∵直线l是⊙O的切线,点A为切点
知识问答
●O
┐
A
l
符号:
圆的切线垂直于经过切点的半径。
∴ l⊥OA
∵ l 经过⊙O上的A点,且l⊥OA
∴直线l是⊙O的切线
条件:
符号:
结论:
结论:
这条直线是圆的切线
一条直线是圆的切线
这条直线:(1)经过切点 (2)垂直于半径
经过半径的外端且垂直于这条半径的直线是圆的切线。
2、切线的性质定理:
例1、如右图所示,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解:直线AB是⊙O的切线 。理由如下:
例题欣赏
∵AB=OA,∠OBA=45°(已知)
∴∠AOB=∠OBA=45°(等边对等角)
∴∠OAB=180°-∠OBA-∠AOB=90°
∴ 直线AB⊥OA
∴直线AB是⊙O的切线
A
B
O
●
自我检测
1、判断题:
2、以三角形的一边为直径的圆恰好与另一边相切,则此三角 形是__________三角形
直角
×
(1) 垂直于圆的半径的直线一定是这个圆的切线。 ( )
(2) 过圆的半径的外端的直线一定是这个圆的切线 。( )
×
4、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
O
●
A
B
C
D
3、课本96页 :练习1、2
5、如右图所示,已知OC平分∠AOB,D是OC上任意一点,⊙D与OA相切于点E。那么,OB是⊙D的切线吗?请说明理由。
E
C
D
●
A
B
O
F
┐
在本节的学习中:
你的收获是 ;
你的疑问是 。
谈一谈
1、如何判定一条直线是已知圆的切线?
(1)只有一个公共点;
(2) d=r
(3)过半径外端且垂直于这条半径的直线是圆的切线;
2、圆的切线有什么性质?
(3)圆的切线垂直于经过切点的半径。
(1)只有一个公共点;
(2) d=r
3、解决切线问题时如何添加辅助线呢?
(1)若直线与圆公共点明确时: 连半径证垂直;
(2)若直线与圆公共点不确定时:作垂线证半径。
(3)若直线和圆相切于某个点时:连半径得垂直。
作业:
课本101至111页 : 4、14 题
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
图(1)中直线l经过半径外端,但不与半径垂直;图(2)(3)中直线l与半径垂直,但不经过半径外端.
从以上反例可以看出,只满足其中一个条件的直线不是圆的切线.必需同时满足,二者缺一不可
切线的判定定理
同课章节目录
