2021届高三三轮回归方法练——12种方法4种思想逐题解析
文档属性
| 名称 | 2021届高三三轮回归方法练——12种方法4种思想逐题解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 964.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览



文档简介
方法1 直接法
1.[2020·广东省七校联合体高三第一次联考试题]已知集合A={x|x2-x-2<0},B={x|x<1},则有( )
A.A∩B={x|0C.A∪B={x|-1【解析】由题意可得A={x|-12.[2020·河南省豫北名校高三质量考评]复数=( )
A.-i B.- i C.-1 D.-i
【解析】由题意可知,===-i,选D
3.[2020·湖南长郡中学10月模拟]已知sin(α+2β)=,cos β=,α,β为锐角,则sin(α+β)的值为( )
A. B. C. D.
【解析】因为cos β=,β为锐角,
所以sin β==,cos 2β=2cos2β-1=-<0
又β为锐角,所以<2β<π
因为α为锐角,所以α+2β∈
又sin(α+2β)=,所以cos(α+2β)=-=-
所以sin(α+β)=sin[(α+2β)-β]=sin(α+2β)cos β-cos(α+2β)sin β
=×-×=
选D
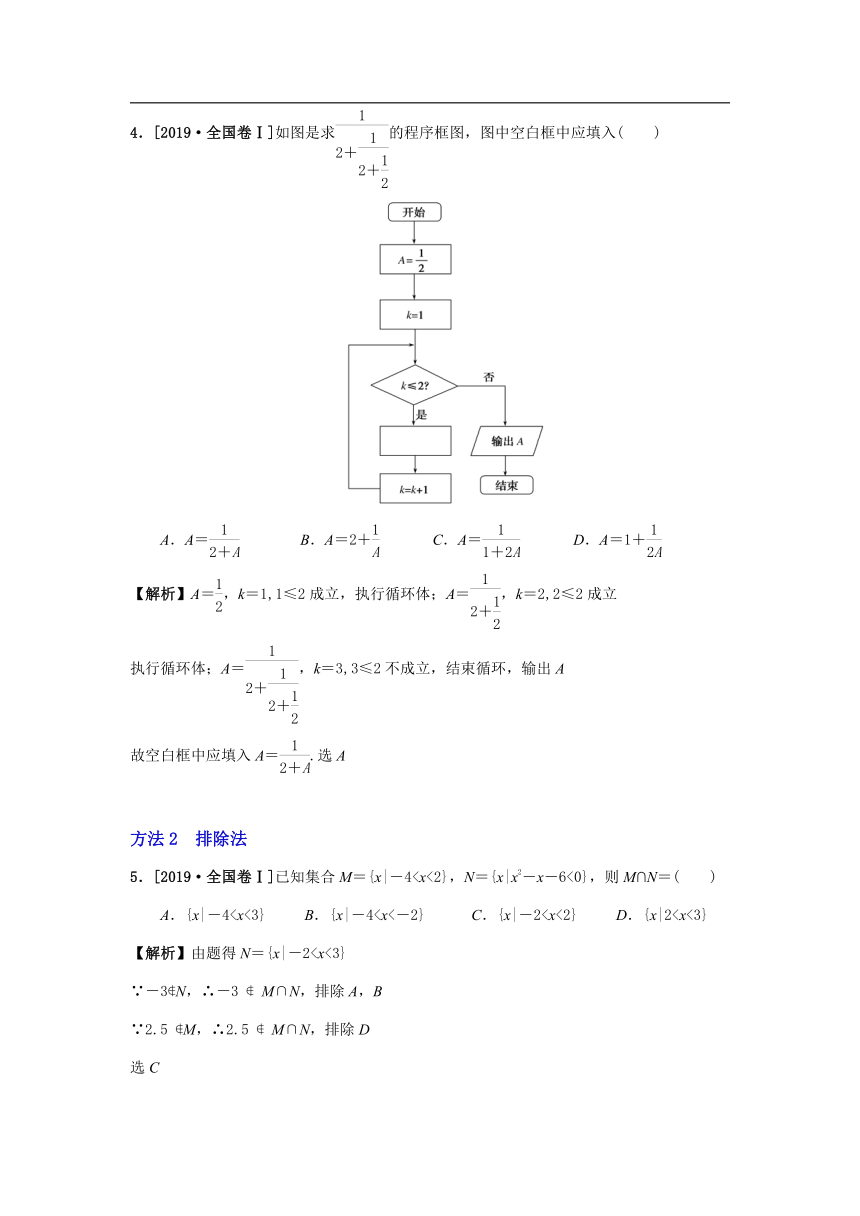
4.[2019·全国卷Ⅰ]如图是求的程序框图,图中空白框中应填入( )
A.A= B.A=2+ C.A= D.A=1+
【解析】A=,k=1,1≤2成立,执行循环体;A=,k=2,2≤2成立
执行循环体;A=,k=3,3≤2不成立,结束循环,输出A
故空白框中应填入A=.选A
方法2 排除法
5.[2019·全国卷Ⅰ]已知集合M={x|-4A.{x|-4【解析】由题得N={x|-2∵-3?N,∴-3 ? M∩N,排除A,B
∵2.5 ?M,∴2.5 ? M∩N,排除D
选C
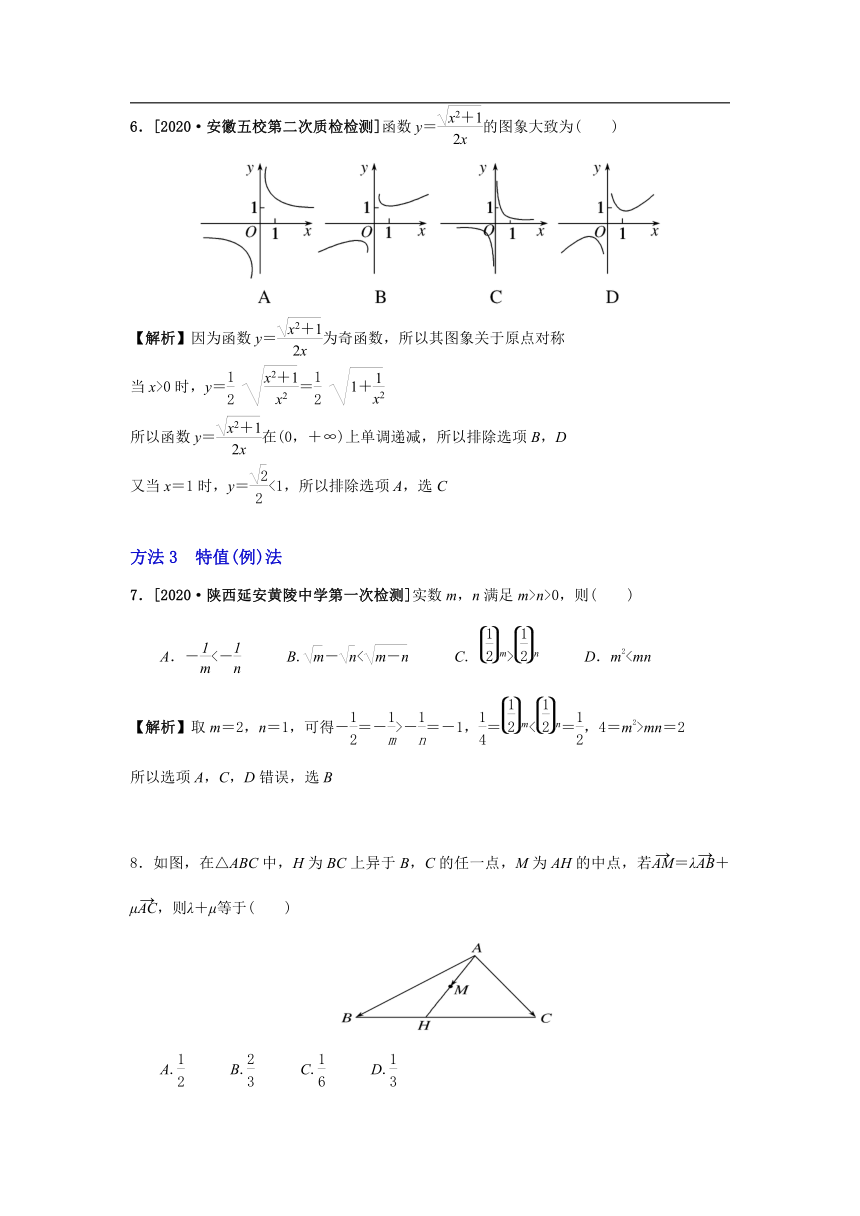
6.[2020·安徽五校第二次质检检测]函数y=的图象大致为( )
【解析】因为函数y=为奇函数,所以其图象关于原点对称
当x>0时,y= =
所以函数y=在(0,+∞)上单调递减,所以排除选项B,D
又当x=1时,y=<1,所以排除选项A,选C
方法3 特值(例)法
7.[2020·陕西延安黄陵中学第一次检测]实数m,n满足m>n>0,则( )
A.-<- B.-< C. m>n D.m2【解析】取m=2,n=1,可得-=->-=-1,=mmn=2
所以选项A,C,D错误,选B
8.如图,在△ABC中,H为BC上异于B,C的任一点,M为AH的中点,若=λ+μ,则λ+μ等于( )
A. B. C. D.
【解法1】(常规法)因为M为AH的中点,且=λ+μ
所以=2=2λ+2μ
因为B,H,C三点共线
所以2λ+2μ=1,所以λ+μ=,选A
【解法2】 (特殊点法)H为BC上异于B,C的任一点时λ+μ都可得到唯一的结果,可取H为BC的中点,则有=+,而==+,所以λ+μ=,选A
【解法3】 (特殊图形+特殊点法)易知△ABC为任意形状时λ+μ都可得到唯一结果,如图所示,在等腰直角三角形ABC中建立平面直角坐标系
设A(0,0),B(0,4),C(4,0),H为BC的中点,则H(2,2),M(1,1)
所以=+,所以λ+μ=,选A
9.[2020·四川遂宁检测]已知ω>,函数f(x)=sin在区间内没有最值,则ω的取值范围是( )
A. B. C. D.
【解法1】 (一般解法)当f(x)取最值时,2ωx+=+kπ,k∈Z,得x=+,k∈Z
依题意得x=+?,k∈Z
令+≤,k∈Z,解得ω≥+k,k∈Z,当k=0时,ω≥
令+≥,k∈Z,解得ω≤+,k∈Z,当k=1时,ω≤
所以ω的取值范围是,选C
【解法2】 (特值解法)根据选项知,当ω=时,f(x)=sin.
因为x∈,所以x+∈,当x+=时f(x)取得最值,不符合题意,排除A,当ω=时,f(x)=sin ,因为x∈,所以x+∈,函数没有最值,符合题意,B,D均未包含ω=,不符合题意,排除B,D.选C.
10.[2019·天津卷]已知函数f(x)=若关于x的方程f(x)=-x+a(a∈R)恰有两个互异的实数解,则a的取值范围为( )
A. B. C.∪{1} D.∪{1}
【解析】(特值解法)根据选项得,当a=时,由得x=37-8
由得x=4,符合题意,排除B,C.
当a=1时,由得x=36-16,由得x=2,符合题意排除A.选D.
方法4 图解法
11.[2020·河南省豫北名校高三质量考评]已知x,y满足约束条件则z=x-2y的最小值为( )
A.0 B.-4 C.- D.1
【解法1】作出可行域,如图中阴影部分所示,作出直线x-2y=0并平移,由图可知当平移后的直线经过点A时,z取得最小值,则zmin=3-2×=-4,故选B.
【解法2】 由 解得此时z=0
由解得此时z=-
由解得此时z=-4
综上所述,z的最小值为-4,选B
12.[2018·全国卷Ⅰ]设函数f(x)=满足f(x+1)A.(-∞,-1] B.(0,+∞) C.(-1,0) D.(-∞,0)
【解析】当x≤0时,函数f(x)=2-x是减函数,则f(x)≥f(0)=1.作出f(x)的大致图象如图所示,结合图象知,使f(x+1)13.[2020·开封市高三模拟试卷]在△ABC中,A=,AB=3,AC=4,动点P在△ABC的内切圆上,若=λ+μ,则λ+μ的最大值为( )
A. B. C.1 D.2
【解法1】以AB所在的直线为x轴,AC所在直线为y轴建立平面直角坐标系,如图
则A(0,0),B(3,0),C(0,4).设内切圆的半径为r
由(||+||+||)r=S△ABC,得r=1
则内切圆的圆心为(1,1),内切圆的标准方程为(x-1)2+(y-1)2=1
设P(1+cos θ,1+sin θ)(θ∈R)
则=(1+cos θ,1+sin θ),=(3,0),=(0,4)
由=λ+μ得
所以λ+μ=(1+cos θ)+(1+sin θ)=+=+sin(θ+φ)(θ∈R,tan φ=)
所以λ+μ的最大值为+=1,选C
【解法2】设△ABC的内切圆与边BC相切于点D
当动点P与点D重合时,P,B,C三点共线
又=λ+μ,则λ+μ=1,当动点P与点D不重合时,λ+μ<1
故λ+μ的最大值为1,选C
14.[2020·广东省模考]函数f(x)=(kx-2)ln x,g(x)=2ln x-x,若f(x)≤g(x)(x∈(1,+∞))的解集中恰有两个整数,则k的取值范围为
【解析】由f(x)≤g(x)得(kx-2)ln x≤2ln x-x,x∈(1,+∞)
当x>1时,ln x>0,则kx-2≤2-,即kx≤4-,x∈(1,+∞)
设h(x)=4-(x>1),则h′(x)=-=-
由h′(x)>0得-(ln x-1)>0,即ln x<1,则1由h′(x)<0得-(ln x-1)<0,即ln x>1,则x>e,所以h(x)在(e,+∞)上单调递减
故当x=e时,h(x)取得极大值h(e)=4-=4-e,当x→1时,h(x)→-∞
h(3)=4-,h(4)=4-=4-=h(2),作出函数h(x)的图象,如图中实线所示
图中点A的坐标为,点B的坐标为
当直线y=kx过点A,B时,斜率分别为kOA==-,kOB==1-
经分析可知要使f(x)≤g(x)(x∈(1,+∞))的解集中恰有两个整数
则直线y=kx的斜率k满足kOB即实数k的取值范围是
方法5 构造法
1.[2020·江西省质量检测]已知可导函数f(x)的导函数为f′(x),若对任意的x∈R,都有f(x)>f′(x)+1,且f(0)=2 020,则不等式f(x)-2 019ex<1的解集为( )
A.(-∞,0) B.(0,+∞) C.(-∞,) D.(,+∞)
【解析】构造函数g(x)=,
则g′(x)=<0,所以函数g(x)=在R上单调递减.
因为f(0)=2 020,所以g(0)==2 019.
由f(x)-2 019ex<1,得f(x)-1<2 019ex,即<2 019,所以g(x)因为函数g(x)在R上单调递减,所以x>0,选B
2.已知m,n∈(2,e),且-A.m>n B.m2+ D.m,n的大小关系不确定
【解析】由不等式可得-即+lnn<+lnm
设f(x)=+ln x(x∈(2,e))
则f′(x)=-+=
因为x∈(2,e),所以f′(x)>0,故函数f(x)在(2,e)上单调递增
因为f(n)3.设数列{an}的前n项和为Sn.若S2=4,an+1=2Sn+1,n∈N*,则a1=________,S5=________
【解析】∵an+1=2Sn+1
∴Sn+1-Sn=2Sn+1
∴Sn+1=3Sn+1,∴Sn+1+=3
∴数列是公比为3的等比数列,∴=3
又S2=4,∴S1=1,∴a1=1
∴S5+=×34=×34=,∴S5=121
4.如图,已知球O的球面上有四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的体积等于________.
【解析】如图,以DA,AB,BC为棱长构造正方体,
设正方体的外接球球O的半径为R,
则正方体的体对角线长即为球O的直径
所以|CD|==2R
所以R=
故球O的体积V==π
方法6 等价转化法
5.设x∈R,若“1≤x≤3”是“|x-a|<2”的充分不必要条件,则实数a的取值范围是( )
A.(1,3) B.[1,3) C.(1,3] D.[1,3]
【解析】由|x-a|<2,解得a-2因为“1≤x≤3”是“|x-a|<2”的充分不必要条件,所以[1,3](a-2,a+2)
所以解得16.不等式mx3≥y3-6x2y对于任意的x∈[2,3],y∈[3,6]恒成立,则m的取值范围是( )
A.[9,+∞) B.[-5,+∞) C.[4,+∞) D.[4,9]
【解析】不等式mx3≥y3-6x2y对于任意的x∈[2,3],y∈[3,6]恒成立
等价于m≥-=-6·对于任意的x∈[2,3],y∈[3,6]恒成立
令t=,则1≤t≤3,所以m≥t3-6t在[1,3]上恒成立
令f(t)=t3-6t(1≤t≤3),则m≥f(t)max
因为f′(t)=3t2-6,由f′(t)>0得所以f(t)在[1,)上单调递减,在(,3]上单调递增
因为f(1)=-5,f(3)=9,所以f(t)max=9,所以m≥9,选A
7.[2020·武汉调研]已知关于x的不等式-x-aln x≥1对于任意的x∈(1,+∞)恒成立,则实数a的取值范围为( )
A.(-∞,1-e] B.(-∞,-3] C.(-∞,-2] D.(-∞,2-e2]
【解析】由题意可知,分离参数得a≤对于任意的x∈(1,+∞)恒成立
令f(x)==(x>1),由题意可知,a≤f(x)min
因为ex-1≥x(当x=0时取等号)
所以f(x)=≥=-3(当x-3ln x=0取等号),所以a≤-3,选B
8.[2020·福建厦门质检]在正三棱锥S ? ABC中,AB=2,SA=2,E,F分别为AC,SB的中点.平面α过点A,α∥平面SBC,α∩平面ABC=l,则异面直线l和EF所成角的余弦值为________
【解析】画出图象如图所示,因为平面α过点A,α∥平面SBC,α∩平面ABC=l,平面SBC∩平面ABC=BC,所以l∥BC
取AB的中点D,连接DE,DF,则DE∥BC,所以l∥DE
所以异面直线l和EF所成角即为∠DEF或其补角
取BC的中点O,连接SO,AO,则SO⊥BC,AO⊥BC
又SO∩AO=O,所以BC⊥平面SOA
又SA?平面SOA,所以BC⊥SA,所以DE⊥DF
在Rt△DEF中,易知DE=,DF=
所以EF=2,cos∠DEF==
所以异面直线l和EF所成角的余弦值为
方法7 待定系数法
9.设y=f(x)是二次函数,方程f(x)=0有两个相等实根,且f′(x)=2x+2,求f(x)的解析式________.
【解析】设f(x)=ax2+bx+c(a≠0),则f′(x)=2ax+b=2x+2
∴a=1,b=2,f(x)=x2+2x+c
又∵方程f(x)=0有两个相等实根
∴Δ=4-4c=0,解得c=1.故f(x)=x2+2x+1
10.衣柜里的樟脑丸,会因为挥发而体积变小,刚放入的新樟脑丸体积为a,经过t天后樟脑丸的体积V(t)与天数t的关系为V(t)=a·e-kt,若新樟脑丸经过80天后,体积变为a,则函数V(t)的解析式为________.
【解析】因为樟脑丸经过80天后,体积变为a
所以a=a·e-80k,所以e-80k=,解得k=-ln
所以V(t)=a·=a·
所以函数V(t)的解析式为V(t)=a· (t≥0)
11.[2020·长沙市四校高三年级模拟考试]已知函数f(x)=Asin(ωx+φ)部分图象如图所示,其中|PQ|=2.则f(x)解析式为________.
【解析】由题图可知A=2,P(x1,-2),Q(x2,2),
所以|PQ|===2,整理得|x1-x2|=2
所以函数f(x)的最小正周期T=2|x1-x2|=4,即=4,解得ω=
又函数图象过点(0,-)
所以2sin φ=-,即sin φ=-
又|φ|<
所以φ=-,所以f(x)=2sin
12.[2020·江西省质量检测]椭圆E:+=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆于A,B两点,交y轴于点C,若F1,C是线段AB的三等分点,△F2AB的周长为4,则椭圆E的标准方程为( )
A.+=1 B.+=1 C.+=1 D.+y2=1
【解析】由椭圆的定义,得|AF1|+|AF2|=|BF1|+|BF2|=2a
所以△F2AB的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=4,所以a=
所以椭圆E:+=1,不妨令点C是F1A的中点,点A在第一象限
因为F1(-c,0),所以点A的横坐标为c,所以+=1,得A
所以C,B
把点B的坐标代入椭圆E的方程,得+=1,即+=1,化简得b2=20-16c2
又b2=5-c2,所以20-16c2=5-c2,得c2=1,所以b2=4
所以椭圆E的标准方程为+=1,选A
方法8 换元法
13.函数y=(x>-1)的最小值为( )
A.1 B.2 C.3 D.4
【解析】设t=x+1,
∴x=t-1,∴y===t+-1≥2-1=1,选A
14.不等式log2(2x-1)·log2(2x+1-2)<2的解集是________.
【解析】设log2(2x-1)=y,则y(y+1)<2,解得-2所以x∈
15.函数f(x)=cos2x-2cos2的一个单调递增区间是( )
A. B. C. D.
【解析】f(x)=cos2x-2cos2=cos2x-cos x-1
令t=cos x∈[-1,1],原函数可以看作g(t)=t2-t-1,t∈[-1,1]
由于对称轴为t=,对于g(t)=t2-t-1
当t∈时,g(t)为减函数,当t∈时,g(t)为增函数
当x∈时,t=cosx为减函数,且t∈
∴原函数在上单调递增,选A
16.设函数f(x)=若方程[f(x)]2+mf(x)+m2-1=0有5个不同的实数根,则实数m的取值范围是________
【解析】根据题意,画出分段函数f(x)的图象,如图中实线所示
令t=f(x),则方程[f(x)]2+mf(x)+m2-1=0有5个不同的实数根可转化为方程t2+mt+m2-1=0有2个不同的实数根
设这两个不同的实数根分别为t1,t2,易知t1≥0,-2令g(t)=t2+mt+m2-1,则,解得-1≤m≤1
∴实数m的取值范围是[-1,1]
方法9 割补法
1.如图所示,虚线网格的最小正方形的边长为1,实线是某几何体的三视图,则这个几何体的体积为( )
A.4π B.2π C. D.π
【解析】依题意可得所求的几何体的直观图如图所示,
把所求的几何体补成圆柱,易知该几何体刚好是底面圆的半径为1,高为4的圆柱的一半,可得这个几何体的体积为V=×π×12×4=2π,选B
2.如图,过正方形ABCD的顶点A作线段PA⊥平面ABCD,若PA=AB,则平面PAB与平面CDP所成二面角的度数为( )
A.90° B.60° C.45° D.30°
【解析】把原四棱锥补成正方体ABCD ? PQRH,如图所示,连接CQ,
则所求二面角转化为平面CDPQ与平面BAPQ所成的二面角,
而∠CQB是平面CDPQ与平面BAPQ所成二面角的平面角,
又因为∠CQB=45°,所以平面PAB与平面CDP所成二面角的度数为45°,选C
3.[2020·江西九江模拟]半正多面体亦称“阿基米德多面体”,是以边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,它由正方体切截而成,以八个正三角形和六个正方形为面,所有的棱都相等.如图是某二十四等边体的三视图,则其体积为( )
A. B.4 C. D.
【解析】该二十四等边体的直观图的示意图如图所示,将其放入正方体中,由三视图可知,二十四等边体的棱长为
它是由棱长为2的正方体沿各棱中点截去8个三棱锥得到的
其体积V=2×2×2-8×××1×1×1=,选D
4.[2020·福州质检]在三棱锥P ? ABC中,PA⊥底面ABC,AB⊥AC,AB=6,AC=8,D是线段AC上一点,且AD=3DC.三棱锥P ? ABC的各个顶点都在球O的表面上,过点D作球O的截面,则所得截面圆的面积的最小值为________.
【解析】如图所示,将三棱锥P ? ABC补成直三棱柱,则三棱锥和该直三棱柱的外接球都是球O,记三角形ABC的外心为O1,连接OO1.
设球O的半径为R,PA=2x,则易知球心O到平面ABC的距离为x,即OO1=x
连接O1A,OA,则O1A=BC=×=5,所以R2=x2+25
在△ABC中,取AC的中点E,连接O1D,O1E,则O1E=AB=3,DE=AC=2
所以O1D==,连接OD,在Rt△OO1D中,OD=
由题意得当过点D的截面与直线OD垂直时,截面面积最小
设此时截面圆的半径为r,则r2=R2-OD2=x2+25-(x2+13)=12
所以所得截面圆的面积的最小值为12π
方法10 整体代换法
5.若函数f(x)是R上单调函数,对任意的实数x有f=,则f(log22 019)=( )
A. B. C. D.1
【解析】假设f(x0)=,则f(x)+=x0,进而f(x)=x0-,从而f(x0)=x0-+1)当x0=1时,f(1)=
因为f(x)是单调函数,所以由f(x0)=,可得x0=1,所以f(x)=1-
所以f(log22 019)=1-=,选C
6.等比数列{an}中,已知a1+a3=8,a5+a7=4,则a9+a11+a13+a15的值为( )
A.1 B.2 C.3 D.5
【解法1】设等比数列{an}的公比为q,则a5=a1q4,a7=a3q4,所以q4===
又a9+a11=a1q8+a3q8=(a1+a3)q8=8×2=2
a13+a15=a1q12+a3q12=(a1+a3)q12=8×3=1
所以a9+a11+a13+a15=2+1=3.
【解法2】因为{an}为等比数列,所以a5+a7是a1+a3与a9+a11的等比中项
所以(a5+a7)2=(a1+a3)(a9+a11),故a9+a11===2
同理,a9+a11是a5+a7与a13+a15的等比中项
所以(a9+a11)2=(a5+a7)(a13+a15),故a13+a15===1
所以a9+a11+a13+a15=2+1=3
7.已知f(x)=ax3+bx+1(ab≠0),若f(2 019)=k,则f(-2 019)=( )
A.k B.-k C.1-k D.2-k
【解析】∵f(2 019)=a·2 0193+b·2 019+1=k
∴a·2 0193+b·2 019=k-1,
则f(-2 019)=a(-2 019)3+b·(-2 019)+1=-[a·2 0193+b·2 019]+1=2-k
8.已知三点A(1,-2),B(a,-1),C(-b,0)共线,则+(a>0,b>0)的最小值为( )
A.11 B.10 C.6 D.4
【解析】由A(1,-2),B(a,-1),C(-b,0)共线得=,整理得2a+b=1
所以+=+=7++≥7+2=11
当且仅当=且2a+b=1即a=,b=时,等号成立,选A
方法11 分离参数法
9.已知函数f(x)=,若不等式f(x)≤kx对任意的x>0恒成立,则实数k的取值范围为________.
【解析】不等式f(x)≤kx对任意的x>0恒成立,即k≥对任意的x>0恒成立
令g(x)=,则g′(x)= =
令g′(x)=0,得x=,且当x∈(0,)时,g′(x)>0,当x∈(,+∞)时,g′(x)<0故当x=时,g(x)取得最大值g()==,所以k≥,即k的取值范围为
10.已知关于x的方程(t+1)cos x-tsin x=t+2在(0,π)上有实根,则实数t的最大值是________.
【解析】由题意可得:-==1-
如图,令P(cos x,sin x),A(2,1),则kPA=
因为x∈(0,π),所以-1<cos x<1,0<sin x≤1
令a=cos x,b=sin x,则点P是上半圆a2+b2=1(-1<a<1,0<b≤1)上任意一点
可知0≤kPA<1,所以0<1-≤1,即0<-≤1,所以t≤-1
故实数t的最大值是-1
11.已知函数f(x)=,ex) (a∈R).若?x∈[1,+∞),不等式f(x)>-1恒成立,求实数a的取值范围________
【解析】∵f(x)>-1?,ex)>-1?2a>x2-ex
∴由条件知,2a>x2-ex对于任意x≥1恒成立
令g(x)=x2-ex,h(x)=g′(x)=2x-ex
则h′(x)=2-ex
当x∈[1,+∞)时,h′(x)=2-ex≤2-e<0
∴h(x)=g′(x)=2x-ex在[1,+∞)上单调递减
∴h(x)=2x-ex≤2-e<0,即g′(x)<0
∴g(x)=x2-ex在[1,+∞)上单调递减
∴g(x)=x2-ex≤g(1)=1-e
故f(x)>-1在[1,+∞)上恒成立,只需2a>g(x)max=1-e
∴a>,故实数a的取值范围是
12.[2020·河南三市联考]已知函数f(x)=x-ln(x+1)对任意的x∈[0,+∞),都有f(x)≤kx2成立,则k的最小值为( )
A.1 B. C.e D.
【解法1】(一般解法)①当k≤0时,取x=1,有f(1)=1-ln 2>0,故k≤0不符合题意.
②当k>0时,令g(x)=f(x)-kx2,即g(x)=x-ln(x+1)-kx2,x≥0
所以g′(x)=1--2kx=-
令g′(x)=0,可得x1=0,x2=>-1
(ⅰ)当k≥时,≤0,g′(x)<0在(0,+∞)上恒成立,g(x)在[0,+∞)上单调递减
所以g(x)≤g(0)=0
所以对任意的x∈[0,+∞),有f(x)≤kx2成立
(ⅱ)当00
当00,g(x)单调递增;当x>时,g′(x)<0,g(x)单调递减
因此存在x0∈使得g(x0)≥g(0)=0
可得x-ln(x0+1)≥kx,即f(x0)≥kx,与题设矛盾,该情况不成立
综上所述,当k≥时,对任意的x∈[0,+∞),都有f(x)≤kx2成立,则k的最小值为
选B
【解法2】(洛必达法则)当x=0时,不等式f(x)≤kx2显然成立
当x≠0时,不等式f(x)≤kx2恒成立可化为k≥=恒成立
因为f′(x)=1-≥0对任意的x∈[0,+∞)恒成立且f′(x)不恒为0
所以f(x)在[0,+∞)上也单调递增,而y=x2在[0,+∞)上单调递增,且其增速比f(x)大
易知满足使用洛必达法则的条件,则有 = = =
可得k≥,选B
方法12 估算法
13.[2020·山东济南部分学校联考]设a=,b=log35,c=log45,则a,b,c的大小关系是( )
A.a<b<c B.a<c<b C.b<c<a D.c<b<a
【解析】因为a=<1,b=log35>c=log45>1,所以a<c<b,选B
14.[2020·济南市高考模拟考试]如图,在多面体ABCDEF中,已知平面ABCD是边长为3的正方形,EF∥AB,EF=,EF与平面ABCD的距离为2,则该多面体的体积为( )
A. B.5 C.6 D.
【解析】连接BE,CE,四棱锥E ? ABCD的体积为VE ? ABCD=×3×3×2=6,
又多面体ABCDEF的体积大于四棱锥E ? ABCD的体积,
即所求几何体的体积V>VE ? ABCD=6,而四个选项里面大于6的只有,选D
15.设A,B,C,D是一个半径为4的球的球面上不共面的四点,△ABC为等边三角形且面积为9,则三棱锥D ? ABC的体积的最大值为( )
A.12 B.18 C.24 D.54
【解法1】由△ABC为等边三角形且面积为9,可得×AB2=9,解得AB=6
设球的球心为O,三角形ABC的外心为O′
则O′C==2,OO′==2,所以三棱锥D?ABC的高的最大值为6
则三棱锥D ?ABC的体积的最大值为××63=18,选B
【解法2】因为球的半径为4
三棱锥D?ABC的体积VD ? ABC=×9h=3h(h为点D到底面三角形ABC的距离,0当h趋近于8时,VD ? ABC趋近于24,所以排除C,D
当h=4时,三角形ABC的外接圆半径为4,则△ABC的面积显然大于9,故可排除A
选B
方法13 函数方程思想
1.[2020·广东揭阳摸底]已知等差数列{an}的前n项和Sn满足S4=5,S9=20,则a7等于( )
A.-3 B.-5 C.3 D.5
【解法1】S9-S4=a5+a6+a7+a8+a9=15,所以5a7=15,所以a7=3.故选C
【解法2】设公差为d,由题意4a1+6d=5,9a1+36d=20,解得a1=,d=,所以a7=3
选C
2.将一个底面半径为1,高为2的圆锥形工件切割成一个圆柱体,能切割出的圆柱的最大体积为( )
A. B. C. D.
【解析】如图所示,设圆柱的半径为r,高为x,体积为V,
由题意可得=,所以x=2-2r,所以圆柱的体积V=πr2(2-2r)=2π(r2-r3)(0由2π(2r-3r2)=0得r=
所以圆柱的最大体积Vmax=2π=
3.[2020·陕西西安二模]已知函数f(x)=x2+4x+4,若存在实数t,当x∈[1,t]时,f(x-a)≤4x(a>0)恒成立,则实数t的最大值是( )
A.4 B.7 C.8 D.9
【解析】作函数f(x)=x2+4x+4=(x+2)2的简图如图所示.由图象可知
当函数y=f(x-a)的图象经过点(1,4)时
有x∈[1,t],f(x-a)≤4x(a>0)恒成立
此时t取最大值,由(1-a)2+4(1-a)+4=4,得a=5或a=1(舍),所以4t=(t-5+2)2
所以t=1(舍)或t=9,故t=9
4.[2018·全国卷Ⅰ]△ABC的内角A,B,C的对边分别为a,b,c.已知bsin C+csin B=4asin Bsin C,b2+c2-a2=8,则△ABC的面积为________.
【解析】∵ bsin C+csin B=4asin Bsin C
∴ 由正弦定理得sin Bsin C+sin Csin B=4sin Asin Bsin C
又sin Bsin C >0,∴ sin A=,由余弦定理得cos A===>0
∴ cos A=,bc==
∴ S△ABC=bcsin A=××=
5.[2020·山东青岛期中联考]已知函数f(x)=x2-2ax+b(a>1)的定义域和值域都为[1,a],则b=________.
【解析】函数f(x)=x2-2ax+b(a>1)图象的对称轴方程为x=-=a>1,
所以函数f(x)=x2-2ax+b在[1,a]上为减函数,
又函数在[1,a]上的值域也为[1,a],∴即
由①得b=3a-1,代入②得a2-3a+2=0,解得a=1(舍)或a=2.
把a=2代入b=3a-1得b=5
6.已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),P是双曲线C右支上一点,且|PF2|=|F1F2|,若直线PF1与圆x2+y2=a2相切,则双曲线的离心率为________.
【解析】取线段PF1的中点为A,连接AF2,又|PF2|=|F1F2|,则AF2⊥PF1,
∵直线PF1与圆x2+y2=a2相切,∴|AF2|=2a,
∵|PA|=|PF1|=a+c,∴4c2=(a+c)2+4a2,化简得(3c-5a)(a+c)=0,
则双曲线的离心率为
7.已知函数f(x)=lg,其中a为常数,若当x∈(-∞,1],f(x)有意义,则实数a的取值范围为________
【解析】由>0,且a2-a+1=2+>0
得1+2x+4x·a>0,故a>-
当x∈(-∞,1]时,y=与y=都是减函数
因此,函数y=-在(-∞,1]上是增函数
所以max=-,所以a>-
故实数a的取值范围是
8.关于x的不等式ex--1-x≥0在x∈上恰成立,则a的取值集合为________.
【解析】关于x的不等式ex--1-x≥0在x∈上恰成立?函数g(x)=在上的值域为
因为g′(x)=
令φ(x)=ex(x-1)-x2+1,x∈,则φ′(x)=x(ex-1)
因为x≥,所以φ′(x)≥0,故φ(x)在上递增,所以φ(x)≥φ=->0
因此g′(x)>0,故g(x)在上单调递增
则g(x)≥g==2-,所以a-=2-,解得a=2
所以a的取值集合为{2}
9.[2020·江苏扬州大学附中月考]已知二次函数g(x)=mx2-2mx+n+1(m>0)在区间[0,3]上有最大值4,最小值0.求函数g(x)的解析式
【解析】g(x)=mx2-2mx+n+1(m>0),易知g(x)图象开口向上,对称轴方程为x=1
∵x∈[0,3],∴当x=1时,g(x)取得最小值-m+n+1=0,①
当x=3时,g(x)取得最大值3m+n+1=4,②
由①②解得m=1,n=0
∴函数g(x)的解析式为g(x)=x2-2x+1
10.[2018·全国卷Ⅱ节选]设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A,B两点,|AB|=8.求l的方程
【解析】由题意得F(1,0),l的方程为y=k(x-1)(k>0)
设A(,),B(,)
由得k2x2-(2k2+4)x+k2=0
Δ=16k2+16>0,故+=
所以|AB|=|AF|+|BF|=(+1)+(+1)=
由题设知=8,解得k=-1(舍去)或k=1
因此l的方程为y=x-1
方法14 数形结合思想
1.[2020·福建省质量检测]在△ABC中,=2,且E为AC的中点,则=( )
A.-+ B.- C.-- D.+
【解法1】如图1,连接AD
=-=-(+)=--(-)=-+.
【解法2】=++=-+=(+)-+=-+.
【解法3】如图2,作=,以,为基底将分解,=+=x+y,则=x+y,易知x<0,y>0,排除B,C,D选项,故选A.
【解法4】不妨令△ABC为直角三角形,C=90°,AC=2,BC=3,以C为坐标原点建立直角坐标系,如图3所示,则C(0,0),A(2,0),B(0,3),D(0,2),E(1,0),
所以=(-2,3),=(-2,0),=(1,-2),易得=-+,选A
2.[2020·广东省联考试题]函数f(x)=的部分图象大致是( )
【解析】因为f(-x)==-f(x)
所以f(x)为奇函数,其图象关于原点对称
当x∈(0,1)时,f(x)=<0
当x∈(1,+∞)时,f(x)>0
选D
3.设双曲线C: -=1(a>0,b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,以F1F2为直径的圆与双曲线左支的一个交点为P.若以A1A2为直径的圆与直线PF2相切,则双曲线C的离心率为( )
A. B. C.2 D.
【解析】如图所示,设以A1A2为直径的圆与直线PF2的切点为Q,连接OQ,则OQ⊥PF2,
又PF1⊥PF2,O为F1F2的中点
所以|PF1|=2|OQ|=2a
又|PF2|-|PF1|=2a
所以|PF2|=4a
在Rt△F1PF2中,|PF1|2+|PF2|2=|F1F2|2?4a2+16a2=20a2=4c2?e==
4.[2020·郑州市质量预测]已知函数f(x)=sin的相邻两条对称轴之间的距离为,将函数f(x)的图象向右平移个单位后,再将所有点的横坐标伸长为原来的2倍,得到g(x)的图象,若g(x)+k=0在x∈有且只有一个实数根,则k的取值范围是( )
A.k≤ B.-1≤k<- C.-【解析】因为f(x)相邻两条对称轴之间的距离为
结合三角函数的图象可知=
又因为T===
所以ω=2,f(x)=sin
将f(x)的图象向右平移个单位得到f(x)=sin=sin,再将所有点的横坐标伸长为原来的2倍得到g(x)=sin,所以方程为sin+k=0
令2x-=t,因为x∈
所以-≤t≤
若g(x)+k=0在x∈上有且只有一个实数根
即g(t)=sin t与y=-k在上有且只有一个交点
-≤-k<或-k=1
即-5.[2018·全国卷Ⅰ]已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)
【解析】令h(x)=-x-a,则g(x)=f(x)-h(x)
在同一坐标系中画出y=f(x),y=h(x)图象的示意图,如图所示
若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象
当直线y=-x-a过点(0,1)时,有2个交点,
此时1=-0-a,a=-1.
当y=-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意
当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意
综上,a的取值范围为[-1,+∞),选C
6.[2020·合肥市高三调研性检测]若实数x,y满足约束条件则z=2x-y的最大值为________.
【解析1】依题意,在坐标平面内画出不等式组表示的平面区域,如图中阴影部分所示,作出直线2x-y=0,平移该直线,当平移到经过点A(3,-2)时,相应直线在y轴上的截距达到最小,此时z=2x-y取得最大值,即zmax=2×3-(-2)=8
【解析2】由得
此时z=8;由得
此时z=4;由得,此时z=-1
综上所述,z=2x-y最大值为8.
7.[2020·武汉市调研测试]过圆O:x2+y2=4外一点P(2,1)作两条互相垂直的直线AB和CD分别交圆O于A,B和C,D点,则四边形ABCD面积的最大值为________.
【解析】如图所示,S四边形ABCD=(PA·PD-PB·PC),取AB,CD的中点分别为E,F,连接OE,OF,OP,
则S四边形ABCD=[(PE+AE)·(PF+DF)-(PE-AE)·(PF-DF)]=PE·DF+AE·PF
由题意知四边形OEPF为矩形,则OE=PF,OF=PE
结合柯西不等式有S四边形ABCD=OF·DF+AE·OE≤
其中OF2+OE2=OP2,DF2+AE2=4-OF2+4-OE2=8-OP2
据此可得S四边形ABCD≤==
综上,四边形ABCD面积的最大值为.
8.[2020·开封市高三模拟试卷]已知函数f(x)是定义域为R的奇函数,满足f(x)+f(2-x)=0,且当x∈(0,1)时,f(x)=x2,则f(1)=________,g(x)=f(x)-|lg x|,则函数g(x)的零点共有______个.
【解析】因为f(x)是定义在R上的奇函数,所以f(0)=0,
因为f(x)+f(2-x)=0,
所以令x=1得f(1)+f(1)=0,即f(1)=0.
由f(x)+f(2-x)=0得f(x)=-f(2-x),
又f(x)是奇函数,
所以-f(2-x)=f(x-2),
即f(x)=f(x-2),
则f(x)是以2为周期的周期函数,
则f(0)=f(2)=0,f(1)=f(3)=0,
即f(n)=0(n∈Z).
注意到f(x)的值域为(-1,1),
由g(x)=0得f(x)=|lg x|<1,因此只需关心函数y=f(x)与y=|lg x|的图象在区间内的公共点个数.
在同一平面直角坐标系内作出函数y=f(x)与y=|lg x|的图象,如图所示,
由图可知,y=f(x)的图象与函数y=|lg x|的图象共有6个交点
因此函数g(x)的零点共有6个
9.已知函数f(x)=2sin2+cos 2x.
(1)求函数f(x)的单调递增区间;
(2)若关于x的方程f(x)-m=2在x∈上有两个不同的解,求实数m取值范围.
【解析】(1)由f(x)=2sin2+cos 2x
=1-cos+cos 2x
=1+sin 2x+cos 2x
=1+2sin,
则由2kπ-≤2x+≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z.
所以函数的单调递增区间为,k∈Z.
(2)
由f(x)-m=2,得f(x)=m+2,
当x∈时,2x+∈,
∵f(0)=1+2sin=1+,函数f(x)的最大值为1+2=3,
∴要使方程f(x)-m=2在x∈上有两个不同的解,则f(x)=m+2在x∈上有两个不同的解,即f(x)和y=m+2在x∈上有两个不同的交点,即1+≤m+2<3
即-1≤m<1.
所以实数m的取值范围为[-1,1).
10.[2020·武汉市质量检测]如图,在棱长为a的正方体ABCD ? A1B1C1D1中,P,Q,L分别为棱A1D1,C1D1,BC的中点.
(1)求证:AC⊥QL;
(2)求点A到平面PQL的距离.
【解析】(1)如图,取DC的中点H,连接QH,HL,BD.在正方体ABCD ? A1B1C1D1中,H,Q分别为DC,C1D1的中点,则QH⊥CD,从而QH⊥平面ABCD,所以QH⊥AC.
在正方形ABCD中,H,L分别为CD,BC的中点,所以BD∥HL,又AC⊥BD,
所以HL⊥AC
又QH∩HL=H,所以AC⊥平面QHL,所以AC⊥QL
(2)取AB的中点M,连接ML,MP,因为M,L分别为AB,BC的中点,所以ML∥AC
又AC⊥QL,所以ML⊥QL,易证PQ∥ML且PQ=ML,所以四边形PQLM为矩形
则点A到平面PQL的距离即点A到平面PML的距离,设其值为h
连接PA,AL,在四面体PAML中,S△AML=AM·BL=··=a2,
S△PML=·ML·PM=·a·=a2
由等体积法可知V三棱锥P ? AML=V三棱锥A ? PML,即·a2·a=·a2·h,解得h=a
故点A到平面PQL的距离为a
方法15 分类讨论思想
1.[2020·开封市高三模拟试卷]设常数a∈R,集合A={x|(x-1)(x-a)≥0},B={x|x≥a-1},若A∪B=R,则a的取值范围为
【解析】若a>1,集合A={x|x≤1或x≥a},
利用数轴可知,要使A∪B=R,需a-1≤1,解得1若a=1,集合A=R,满足A∪B=R,故a=1符合题意;
若a<1,集合A={x|x≤a或x≥1},利用数轴可知,显然满足A∪B=R,故a<1符合题意.
综上,a的取值范围为(-∞,2]
2.已知a>0,b>0,且a≠1,b≠1,若logab>1,则( )
A.(a-1)(b-1)<0 B.(a-1)(a-b)>0 C.(b-1)(b-a)<0 D.(b-1)(b-a)>0
【解析】∵a>0,b>0,且a≠1,b≠1
∴当a>1,即a-1>0时,不等式logab>1可化为alogab>a1,即b>a>1
∴(a-1)(a-b)<0,(a-1)(b-1)>0,(b-1)(b-a)>0
当01可化为alogab∴(a-1)(a-b)<0,(a-1)(b-1)>0,(b-1)(b-a)>0
综上可知,选D
3.若双曲线+=1的渐近线方程为y=±x,则m的值
【解析】根据题意可分以下两种情况讨论:
①当焦点在x轴上时,则有解得m<1
此时渐近线方程为y=± x,由题意得,=,解得m=
②当焦点在y轴上时,则有解得m>3
此时渐近线方程为y=± x,由题意得,=,无解
综上可知m=
4.[2020·湖北武汉调研]已知实数x,y满足约束条件如果目标函数z=x+ay的最大值为,则实数a的值为( )
A.3 B. C.3或 D.3或-
【解析】先画出线性约束条件所表示的可行域,目标函数化为y=-x+z,目标函数z=x+ay的最大值只需直线的截距最大,
当a>0时,-<0,
①若-<-<0,即a>2,最优解为A,
z=+a=,a=3,符合题意;
②若-<-,即0z=3+a=,a=,不符合题意,舍去.
当a<0时,->0,
③若0<-<1,即a<-1,最优解为C(-2,-2),
z=-2-2a=,a=-,符合题意;
④若->1,即-1z=3+a=,a=,不符合题意,舍去;
综上可知实数a的值为3或-.故选D.
5.[2020·江西师范附属中学模拟]已知f(x)=,若f(2-a)=1,则f(a)等于( )
A.-2 B.-1 C.1 D.2
【解析】①当2-a≥2,即a≤0时,22-a-2-1=1,解得a=-1
则f(a)=f(-1)=-log2[3-(-1)]=-2
②当2-a<2即a>0时,-log2[3-(2-a)]=1
解得a=-,舍去
所以f(a)=-2.故选A
6.[2020·安徽阜阳二模]等比数列{an}中,a1+a4+a7=2,a3+a6+a9=18,则{an}的前9项和S9=________
【解析】由题意得q2==9,q=±3
①当q=3时,a2+a5+a8=3(a1+a4+a7)=6,S9=2+6+18=26
②当q=-3时,a2+a5+a8=-3(a1+a4+a7)=-6,S9=2-6+18=14
所以S9=14或26
7.设圆锥曲线Γ的两个焦点分别为F1,F2.若曲线Γ上存在点P满足|PF1|:|F1F2|:|PF2|=4:3:2,则曲线Γ的离心率等于________
【解析】设|F1F2|=2c(c>0)
由已知|PF1|︰|F1F2|︰|PF2|=4︰3︰2
得|PF1|=c,|PF2|=c,且|PF1|>|PF2|
若圆锥曲线Γ为椭圆,则2a=|PF1|+|PF2|=4c,离心率e=
若圆锥曲线Γ为双曲线,则2a=|PF1|-|PF2|=c,离心率e=
故曲线Γ的离心率等于或
8.f(x)是定义在R上的函数,满足f(x)=f(-x),且x≥0时,f(x)=x3,若对任意的x∈[2t-1,2t+3],不等式f(3x-t)≥8f(x)恒成立,则实数t的取值范围是________.
【解析】f(x)是定义在R上的偶函数,f(x)=x3,在x>0上为单调增函数,
f(3x-t)≥8f(x)=8x3=f(2x),
|3x-t|≥|2x|,所以(3x-t)2≥(2x)2,化简得5x2-6xt+t2≥0.(*)
①当t=0时显然成立;
②当t>0时,(*)式解为x≤或x≥t,对任意x∈[2t-1,2t+3],(*)式恒成立,则需t≤2t-1,故t≥1;
③当t<0时,(*)式解为x≤t或t≥,对任意x∈[2t-1,2t+3],
(*)式恒成立,则需2t+3≤t,故t≤-3.
综上所述,t≤-3或t≥1或t=0.
9.已知a,b,c分别是△ABC的内角A,B,C所对的边,a=2bcos B,b≠c.
(1)证明:A=2B;
(2)若a2+c2=b2+2acsin C,求A.
【解析】(1)证明:∵a=2bcos B,且=,∴sin A=2sin Bcos B=sin 2B
∵00,∴0<2B<π,∴A=2B或A+2B=π
若A+2B=π,则B=C,b=c,这与“b≠c”矛盾,∴A+2B≠π,∴A=2B
(2)∵a2+c2=b2+2,∴=sin C,由余弦定理得cos B=sin C
∵0①当C=-B时,由A=2B且A+B+C=π,得A=,B=C=,这与“b≠c”矛盾,∴A≠
②当C=+B时,由(1)得A=2B,∴A+B+C=A+2B+=2A+=π,∴A=
综上,A=
10.[2020·河南省豫北名校高三质量考评]已知函数f(x)=2ax-aex-1(a≠0).
(1)求函数f(x)的单调区间;
(2)若f(x)≤e-2-(a+1)ex对任意x∈[1,2]恒成立,求实数a的取值范围.
【解析】(1)由题意得f′(x)=2a-aex=a(2-ex).
令f′(x)=0,得x=ln 2.
当a>0时,由f′(x)>0,得xln 2,
所以f(x)的单调递增区间为(-∞,ln 2),单调递减区间为(ln 2,+∞);
当a<0时,则易得f(x)的单调递增区间为(ln 2,+∞),单调递减区间为(-∞,ln 2).
(2)f(x)≤e-2-(a+1)ex(a≠0)对任意x∈[1,2]恒成立,即2ax-aex-1≤e-2-(a+1)ex(a≠0)对任意x∈[1,2]恒成立,即2ax+ex+1-e≤0(a≠0)对任意x∈[1,2]恒成立.
令F(x)=2ax+ex+1-e(a≠0),则F′(x)=2a+ex(a≠0),
当a>0时,F′(x)=2a+ex>0,F(x)在[1,2]上单调递增,
F(1)=2a+1>0,F(x)≤0在[1,2]上不成立,不满足题意.
当a<0时,由F′(x)=0,得x=ln(-2a),当x∈(-∞,ln(-2a))时F′(x)<0,F(x)单调递减;当x∈(ln(-2a),+∞)时,F′(x)>0,F(x)单调递增.
若ln(-2a)≤1,即-≤a<0,则F(x)在[1,2]上单调递增,
由F(2)=4a+e2-e+1≤0,得a≤,又-≤a<0,所以不存在满足题意的a.
若1则F(x)在[1,ln(-2a))上单调递减,在(ln(-2a),2]上单调递增,
由F(1)=2a+1≤0,得a≤-,由F(2)=4a+e2-e+1≤0,得a≤,
又-若ln(-2a)≥2,即a≤-,则F(x)在[1,2]上单调递减,
由F(1)=2a+1≤0,得a≤-,又a≤-,所以a≤-.
综上所述,a的取值范围为
方法16 转化化归思想
1.[2020·湖南衡阳联考]设正项等差数列{an}的前n项和为Sn,若S2 019=6 057,则+的最小值为( )
A.1 B. C. D.
【解析】依题意得(a1+a2 019)=6 057?a1+a2 019=a2+a2 018=6,
+=(a2+a2 018)=≥,仅当a2=2,a2 018=4时取等号
选D.
2.设f(x)是奇函数,对任意的实数x,y,有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,则f(x)在区间[a,b]上( )
A.有最小值f(a) B.有最大值f(a) C.有最大值f D.有最小值f
【解法1】因为f(x)是奇函数,且对任意的实数x,y,有f(x+y)=f(x)+f(y),
则f(0)=0,当x>0时,f(x)<0,则当x<0时,f(x)>0,
对任意x1,x2∈R,f(x+y)=f(x)+f(y),当x1总有f(x1-x2)=f(x1)+f(-x2)=f(x1)-f(x2),
因为x1-x2<0,所以f(x1-x2)>0,即f(x1)-f(x2)>0,故f(x)在R上是减函数,故f(x)在区间[a,b]上有最大值f(a).故选B.
【解法2】f(x)=-x显然符合条件,易得f(x)=-x在区间[a,b]上有最大值f(a),选B
3.已知H为△ABC的垂心,AB=4,AC=6,M为边BC的中点,则·=( )
A.20 B.10 C.-20 D.-10
【解法1】如图所示,因为H为△ABC的垂心,
所以⊥,所以·=0,
又AB=4,AC=6,且M为边BC的中点,
所以·=(++)·=·=·+·
=(+)·(-)=(2-2)=×(36-16)=10,选B
【解法2】将△ABC特殊化为直角三角形,建立如图所示的平面直角坐标系,根据AB=4,AC=6,得B(0,4),C(6,0),M(3,2),H(0,0),
所以·=(3,2)·(6,-4)=10.故选B.
4.[2020·南昌师大附中模拟]函数f(x)=ln x+x2-ax(x>0)在区间上有且仅有一个极值点,则实数a的取值范围是( )
A. B. C. D.
【解析】由f(x)=ln x+x2-ax(x>0)得f′(x)=+x-a(x>0).
因为函数f(x)=ln x+x2-ax在区间上有且仅有一个极值点,
所以y=f′(x)在区间上有且仅有一个变号零点.
令f′(x)=+x-a=0,得a=+x,令g(x)=+x,x∈,则g(x)在区间上单调递减,在区间(1,3]上单调递增,所以g(x)min=g(1)=2.
又g=g(2)=,g(3)=,结合函数g(x)=+x,x∈的图象(图略)可得,
当≤a<时,y=f′(x)在区间上有且仅有一个变号零点.
所以实数a的取值范围为,故选B.
5.若二次函数f(x)=4x2-2(p-2)x-2p2-p+1在区间[-1,1]内至少存在一个值c,使得f(c)>0,则实数p的取值范围是____________.
【解析】如果在[-1,1]内没有值满足f(c)>0,则?
?p≤-3或p≥,取补集为-3故实数p的取值范围为
6.对于满足0≤p≤4的所有实数p,使不等式x2+px>4x+p-3成立的x的取值范围是______.
【解析】设f(p)=(x-1)p+x2-4x+3,则当x=1时,f(p)=0,所以x≠1.
f(p)在0≤p≤4上恒为正,等价于即解得x>3或x<-1
7.[2020·郑州市质检]函数f(x)=x3+3ax-1,g(x)=f′(x)-ax-5,其中f′(x)是f(x)的导函数.对满足-1≤a≤1的一切a的值,都有g(x)<0,则实数x的取值范围为________.
【解析】由题意,知g(x)=3x2-ax+3a-5,
令φ(a)=(3-x)a+3x2-5,-1≤a≤1.
对-1≤a≤1,恒有g(x)<0,即φ(a)<0,
所以即解得-故当x∈时,对满足-1≤a≤1的一切a的值,都有g(x)<0.
8.[2020·南京模拟]若函数f(x)=-ln(x+1)不存在零点,则实数k的范围是_______
【解析】由x+1>0得x>-1,由kx>0得
当=ln(x+1)时,由对数的性质可得ln(kx)=2ln(x+1)=ln(x+1)2,
即kx=(x+1)2,变形可得k==x++2(x>-1且x≠0),
易知当-10时,x+≥2,所以当-10时,x++2≥4,
要使函数f(x)=-ln(x+1)不存在零点,
只需k取x++2(x>-1且x≠0)的取值集合的补集,即{k|0≤k<4},
当k=0时,函数无意义,故k的取值范围是(0,4).
9.若对于任意t∈[1,2],函数g(x)=x3+x2-2x在区间(t,3)上总不为单调函数,求实数m的取值范围
【解析】g′(x)=3x2+(m+4)x-2
若g(x)在区间(t,3)上总为单调函数
则①g′(x)≥0在(t,3)上恒成立,或②g′(x)≤0在(t,3)上恒成立.(正反转化)
由①得3x2+(m+4)x-2≥0,即m+4≥-3x
当x∈(t,3)时恒成立,∴m+4≥-3t恒成立
则m+4≥-1,即m≥-5
由②得3x2+(m+4)x-2≤0,即m+4≤-3x
当x∈(t,3)时恒成立
则m+4≤-9,即m≤-
∴函数g(x)在区间(t,3)上总不为单调函数的m的取值范围为
10.[2020·开封市高三模拟试卷]如图,点O为长方形ABCD的中心,EC⊥平面ABCD,BC=2CD=2,EC=2,M是线段ED上不同于E的动点,N是线段AC上的动点.
(1)求证:平面ABE⊥平面CBE;(2)求二面角M ? BE ? N的取值范围.
【解析】(1)EC⊥平面ABCD,AB?平面ABCD,所以EC⊥AB,
长方形ABCD中,CB⊥AB,又EC∩CB=C,所以AB⊥平面CBE,
又AB?平面ABE,所以平面ABE⊥平面CBE.
(2)以C为坐标原点,的方向为x轴正方向,|C|为单位长度,建立如图所示的空间直角坐标系C?xyz,连接BD,则AC与BD交于点O,连接OE,
半平面BEM即半平面BED,C(0,0,0),D(1,0,0),O,B(0,2,0),E(0,0,2)
因为AB⊥平面CBE,所以CD⊥平面CBE,所以平面CBE的一个法向量为=(1,0,0),
设平面BEO的法向量为m=(x,y,z),又=,=(0,-2,2),
所以,即,令z=1,则m=(2,,1),
所以cos〈,m〉==,二面角O ? BE ? C的大小为.
又由(1)可知,二面角C ? BE ? A的大小为,所以二面角O ? BE ? A的大小为,当N位于点O时,二面角M ? BE ? N的大小为0,所以二面角M ?BE?N的取值范围是
1.[2020·广东省七校联合体高三第一次联考试题]已知集合A={x|x2-x-2<0},B={x|x<1},则有( )
A.A∩B={x|0
A.-i B.- i C.-1 D.-i
【解析】由题意可知,===-i,选D
3.[2020·湖南长郡中学10月模拟]已知sin(α+2β)=,cos β=,α,β为锐角,则sin(α+β)的值为( )
A. B. C. D.
【解析】因为cos β=,β为锐角,
所以sin β==,cos 2β=2cos2β-1=-<0
又β为锐角,所以<2β<π
因为α为锐角,所以α+2β∈
又sin(α+2β)=,所以cos(α+2β)=-=-
所以sin(α+β)=sin[(α+2β)-β]=sin(α+2β)cos β-cos(α+2β)sin β
=×-×=
选D
4.[2019·全国卷Ⅰ]如图是求的程序框图,图中空白框中应填入( )
A.A= B.A=2+ C.A= D.A=1+
【解析】A=,k=1,1≤2成立,执行循环体;A=,k=2,2≤2成立
执行循环体;A=,k=3,3≤2不成立,结束循环,输出A
故空白框中应填入A=.选A
方法2 排除法
5.[2019·全国卷Ⅰ]已知集合M={x|-4
∵2.5 ?M,∴2.5 ? M∩N,排除D
选C
6.[2020·安徽五校第二次质检检测]函数y=的图象大致为( )
【解析】因为函数y=为奇函数,所以其图象关于原点对称
当x>0时,y= =
所以函数y=在(0,+∞)上单调递减,所以排除选项B,D
又当x=1时,y=<1,所以排除选项A,选C
方法3 特值(例)法
7.[2020·陕西延安黄陵中学第一次检测]实数m,n满足m>n>0,则( )
A.-<- B.-< C. m>n D.m2
所以选项A,C,D错误,选B
8.如图,在△ABC中,H为BC上异于B,C的任一点,M为AH的中点,若=λ+μ,则λ+μ等于( )
A. B. C. D.
【解法1】(常规法)因为M为AH的中点,且=λ+μ
所以=2=2λ+2μ
因为B,H,C三点共线
所以2λ+2μ=1,所以λ+μ=,选A
【解法2】 (特殊点法)H为BC上异于B,C的任一点时λ+μ都可得到唯一的结果,可取H为BC的中点,则有=+,而==+,所以λ+μ=,选A
【解法3】 (特殊图形+特殊点法)易知△ABC为任意形状时λ+μ都可得到唯一结果,如图所示,在等腰直角三角形ABC中建立平面直角坐标系
设A(0,0),B(0,4),C(4,0),H为BC的中点,则H(2,2),M(1,1)
所以=+,所以λ+μ=,选A
9.[2020·四川遂宁检测]已知ω>,函数f(x)=sin在区间内没有最值,则ω的取值范围是( )
A. B. C. D.
【解法1】 (一般解法)当f(x)取最值时,2ωx+=+kπ,k∈Z,得x=+,k∈Z
依题意得x=+?,k∈Z
令+≤,k∈Z,解得ω≥+k,k∈Z,当k=0时,ω≥
令+≥,k∈Z,解得ω≤+,k∈Z,当k=1时,ω≤
所以ω的取值范围是,选C
【解法2】 (特值解法)根据选项知,当ω=时,f(x)=sin.
因为x∈,所以x+∈,当x+=时f(x)取得最值,不符合题意,排除A,当ω=时,f(x)=sin ,因为x∈,所以x+∈,函数没有最值,符合题意,B,D均未包含ω=,不符合题意,排除B,D.选C.
10.[2019·天津卷]已知函数f(x)=若关于x的方程f(x)=-x+a(a∈R)恰有两个互异的实数解,则a的取值范围为( )
A. B. C.∪{1} D.∪{1}
【解析】(特值解法)根据选项得,当a=时,由得x=37-8
由得x=4,符合题意,排除B,C.
当a=1时,由得x=36-16,由得x=2,符合题意排除A.选D.
方法4 图解法
11.[2020·河南省豫北名校高三质量考评]已知x,y满足约束条件则z=x-2y的最小值为( )
A.0 B.-4 C.- D.1
【解法1】作出可行域,如图中阴影部分所示,作出直线x-2y=0并平移,由图可知当平移后的直线经过点A时,z取得最小值,则zmin=3-2×=-4,故选B.
【解法2】 由 解得此时z=0
由解得此时z=-
由解得此时z=-4
综上所述,z的最小值为-4,选B
12.[2018·全国卷Ⅰ]设函数f(x)=满足f(x+1)
【解析】当x≤0时,函数f(x)=2-x是减函数,则f(x)≥f(0)=1.作出f(x)的大致图象如图所示,结合图象知,使f(x+1)
A. B. C.1 D.2
【解法1】以AB所在的直线为x轴,AC所在直线为y轴建立平面直角坐标系,如图
则A(0,0),B(3,0),C(0,4).设内切圆的半径为r
由(||+||+||)r=S△ABC,得r=1
则内切圆的圆心为(1,1),内切圆的标准方程为(x-1)2+(y-1)2=1
设P(1+cos θ,1+sin θ)(θ∈R)
则=(1+cos θ,1+sin θ),=(3,0),=(0,4)
由=λ+μ得
所以λ+μ=(1+cos θ)+(1+sin θ)=+=+sin(θ+φ)(θ∈R,tan φ=)
所以λ+μ的最大值为+=1,选C
【解法2】设△ABC的内切圆与边BC相切于点D
当动点P与点D重合时,P,B,C三点共线
又=λ+μ,则λ+μ=1,当动点P与点D不重合时,λ+μ<1
故λ+μ的最大值为1,选C
14.[2020·广东省模考]函数f(x)=(kx-2)ln x,g(x)=2ln x-x,若f(x)≤g(x)(x∈(1,+∞))的解集中恰有两个整数,则k的取值范围为
【解析】由f(x)≤g(x)得(kx-2)ln x≤2ln x-x,x∈(1,+∞)
当x>1时,ln x>0,则kx-2≤2-,即kx≤4-,x∈(1,+∞)
设h(x)=4-(x>1),则h′(x)=-=-
由h′(x)>0得-(ln x-1)>0,即ln x<1,则1
故当x=e时,h(x)取得极大值h(e)=4-=4-e,当x→1时,h(x)→-∞
h(3)=4-,h(4)=4-=4-=h(2),作出函数h(x)的图象,如图中实线所示
图中点A的坐标为,点B的坐标为
当直线y=kx过点A,B时,斜率分别为kOA==-,kOB==1-
经分析可知要使f(x)≤g(x)(x∈(1,+∞))的解集中恰有两个整数
则直线y=kx的斜率k满足kOB
方法5 构造法
1.[2020·江西省质量检测]已知可导函数f(x)的导函数为f′(x),若对任意的x∈R,都有f(x)>f′(x)+1,且f(0)=2 020,则不等式f(x)-2 019ex<1的解集为( )
A.(-∞,0) B.(0,+∞) C.(-∞,) D.(,+∞)
【解析】构造函数g(x)=,
则g′(x)=<0,所以函数g(x)=在R上单调递减.
因为f(0)=2 020,所以g(0)==2 019.
由f(x)-2 019ex<1,得f(x)-1<2 019ex,即<2 019,所以g(x)
2.已知m,n∈(2,e),且-
【解析】由不等式可得-
设f(x)=+ln x(x∈(2,e))
则f′(x)=-+=
因为x∈(2,e),所以f′(x)>0,故函数f(x)在(2,e)上单调递增
因为f(n)
【解析】∵an+1=2Sn+1
∴Sn+1-Sn=2Sn+1
∴Sn+1=3Sn+1,∴Sn+1+=3
∴数列是公比为3的等比数列,∴=3
又S2=4,∴S1=1,∴a1=1
∴S5+=×34=×34=,∴S5=121
4.如图,已知球O的球面上有四点A,B,C,D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的体积等于________.
【解析】如图,以DA,AB,BC为棱长构造正方体,
设正方体的外接球球O的半径为R,
则正方体的体对角线长即为球O的直径
所以|CD|==2R
所以R=
故球O的体积V==π
方法6 等价转化法
5.设x∈R,若“1≤x≤3”是“|x-a|<2”的充分不必要条件,则实数a的取值范围是( )
A.(1,3) B.[1,3) C.(1,3] D.[1,3]
【解析】由|x-a|<2,解得a-2
所以解得1
A.[9,+∞) B.[-5,+∞) C.[4,+∞) D.[4,9]
【解析】不等式mx3≥y3-6x2y对于任意的x∈[2,3],y∈[3,6]恒成立
等价于m≥-=-6·对于任意的x∈[2,3],y∈[3,6]恒成立
令t=,则1≤t≤3,所以m≥t3-6t在[1,3]上恒成立
令f(t)=t3-6t(1≤t≤3),则m≥f(t)max
因为f′(t)=3t2-6,由f′(t)>0得
因为f(1)=-5,f(3)=9,所以f(t)max=9,所以m≥9,选A
7.[2020·武汉调研]已知关于x的不等式-x-aln x≥1对于任意的x∈(1,+∞)恒成立,则实数a的取值范围为( )
A.(-∞,1-e] B.(-∞,-3] C.(-∞,-2] D.(-∞,2-e2]
【解析】由题意可知,分离参数得a≤对于任意的x∈(1,+∞)恒成立
令f(x)==(x>1),由题意可知,a≤f(x)min
因为ex-1≥x(当x=0时取等号)
所以f(x)=≥=-3(当x-3ln x=0取等号),所以a≤-3,选B
8.[2020·福建厦门质检]在正三棱锥S ? ABC中,AB=2,SA=2,E,F分别为AC,SB的中点.平面α过点A,α∥平面SBC,α∩平面ABC=l,则异面直线l和EF所成角的余弦值为________
【解析】画出图象如图所示,因为平面α过点A,α∥平面SBC,α∩平面ABC=l,平面SBC∩平面ABC=BC,所以l∥BC
取AB的中点D,连接DE,DF,则DE∥BC,所以l∥DE
所以异面直线l和EF所成角即为∠DEF或其补角
取BC的中点O,连接SO,AO,则SO⊥BC,AO⊥BC
又SO∩AO=O,所以BC⊥平面SOA
又SA?平面SOA,所以BC⊥SA,所以DE⊥DF
在Rt△DEF中,易知DE=,DF=
所以EF=2,cos∠DEF==
所以异面直线l和EF所成角的余弦值为
方法7 待定系数法
9.设y=f(x)是二次函数,方程f(x)=0有两个相等实根,且f′(x)=2x+2,求f(x)的解析式________.
【解析】设f(x)=ax2+bx+c(a≠0),则f′(x)=2ax+b=2x+2
∴a=1,b=2,f(x)=x2+2x+c
又∵方程f(x)=0有两个相等实根
∴Δ=4-4c=0,解得c=1.故f(x)=x2+2x+1
10.衣柜里的樟脑丸,会因为挥发而体积变小,刚放入的新樟脑丸体积为a,经过t天后樟脑丸的体积V(t)与天数t的关系为V(t)=a·e-kt,若新樟脑丸经过80天后,体积变为a,则函数V(t)的解析式为________.
【解析】因为樟脑丸经过80天后,体积变为a
所以a=a·e-80k,所以e-80k=,解得k=-ln
所以V(t)=a·=a·
所以函数V(t)的解析式为V(t)=a· (t≥0)
11.[2020·长沙市四校高三年级模拟考试]已知函数f(x)=Asin(ωx+φ)部分图象如图所示,其中|PQ|=2.则f(x)解析式为________.
【解析】由题图可知A=2,P(x1,-2),Q(x2,2),
所以|PQ|===2,整理得|x1-x2|=2
所以函数f(x)的最小正周期T=2|x1-x2|=4,即=4,解得ω=
又函数图象过点(0,-)
所以2sin φ=-,即sin φ=-
又|φ|<
所以φ=-,所以f(x)=2sin
12.[2020·江西省质量检测]椭圆E:+=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆于A,B两点,交y轴于点C,若F1,C是线段AB的三等分点,△F2AB的周长为4,则椭圆E的标准方程为( )
A.+=1 B.+=1 C.+=1 D.+y2=1
【解析】由椭圆的定义,得|AF1|+|AF2|=|BF1|+|BF2|=2a
所以△F2AB的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=4,所以a=
所以椭圆E:+=1,不妨令点C是F1A的中点,点A在第一象限
因为F1(-c,0),所以点A的横坐标为c,所以+=1,得A
所以C,B
把点B的坐标代入椭圆E的方程,得+=1,即+=1,化简得b2=20-16c2
又b2=5-c2,所以20-16c2=5-c2,得c2=1,所以b2=4
所以椭圆E的标准方程为+=1,选A
方法8 换元法
13.函数y=(x>-1)的最小值为( )
A.1 B.2 C.3 D.4
【解析】设t=x+1,
∴x=t-1,∴y===t+-1≥2-1=1,选A
14.不等式log2(2x-1)·log2(2x+1-2)<2的解集是________.
【解析】设log2(2x-1)=y,则y(y+1)<2,解得-2
15.函数f(x)=cos2x-2cos2的一个单调递增区间是( )
A. B. C. D.
【解析】f(x)=cos2x-2cos2=cos2x-cos x-1
令t=cos x∈[-1,1],原函数可以看作g(t)=t2-t-1,t∈[-1,1]
由于对称轴为t=,对于g(t)=t2-t-1
当t∈时,g(t)为减函数,当t∈时,g(t)为增函数
当x∈时,t=cosx为减函数,且t∈
∴原函数在上单调递增,选A
16.设函数f(x)=若方程[f(x)]2+mf(x)+m2-1=0有5个不同的实数根,则实数m的取值范围是________
【解析】根据题意,画出分段函数f(x)的图象,如图中实线所示
令t=f(x),则方程[f(x)]2+mf(x)+m2-1=0有5个不同的实数根可转化为方程t2+mt+m2-1=0有2个不同的实数根
设这两个不同的实数根分别为t1,t2,易知t1≥0,-2
∴实数m的取值范围是[-1,1]
方法9 割补法
1.如图所示,虚线网格的最小正方形的边长为1,实线是某几何体的三视图,则这个几何体的体积为( )
A.4π B.2π C. D.π
【解析】依题意可得所求的几何体的直观图如图所示,
把所求的几何体补成圆柱,易知该几何体刚好是底面圆的半径为1,高为4的圆柱的一半,可得这个几何体的体积为V=×π×12×4=2π,选B
2.如图,过正方形ABCD的顶点A作线段PA⊥平面ABCD,若PA=AB,则平面PAB与平面CDP所成二面角的度数为( )
A.90° B.60° C.45° D.30°
【解析】把原四棱锥补成正方体ABCD ? PQRH,如图所示,连接CQ,
则所求二面角转化为平面CDPQ与平面BAPQ所成的二面角,
而∠CQB是平面CDPQ与平面BAPQ所成二面角的平面角,
又因为∠CQB=45°,所以平面PAB与平面CDP所成二面角的度数为45°,选C
3.[2020·江西九江模拟]半正多面体亦称“阿基米德多面体”,是以边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,它由正方体切截而成,以八个正三角形和六个正方形为面,所有的棱都相等.如图是某二十四等边体的三视图,则其体积为( )
A. B.4 C. D.
【解析】该二十四等边体的直观图的示意图如图所示,将其放入正方体中,由三视图可知,二十四等边体的棱长为
它是由棱长为2的正方体沿各棱中点截去8个三棱锥得到的
其体积V=2×2×2-8×××1×1×1=,选D
4.[2020·福州质检]在三棱锥P ? ABC中,PA⊥底面ABC,AB⊥AC,AB=6,AC=8,D是线段AC上一点,且AD=3DC.三棱锥P ? ABC的各个顶点都在球O的表面上,过点D作球O的截面,则所得截面圆的面积的最小值为________.
【解析】如图所示,将三棱锥P ? ABC补成直三棱柱,则三棱锥和该直三棱柱的外接球都是球O,记三角形ABC的外心为O1,连接OO1.
设球O的半径为R,PA=2x,则易知球心O到平面ABC的距离为x,即OO1=x
连接O1A,OA,则O1A=BC=×=5,所以R2=x2+25
在△ABC中,取AC的中点E,连接O1D,O1E,则O1E=AB=3,DE=AC=2
所以O1D==,连接OD,在Rt△OO1D中,OD=
由题意得当过点D的截面与直线OD垂直时,截面面积最小
设此时截面圆的半径为r,则r2=R2-OD2=x2+25-(x2+13)=12
所以所得截面圆的面积的最小值为12π
方法10 整体代换法
5.若函数f(x)是R上单调函数,对任意的实数x有f=,则f(log22 019)=( )
A. B. C. D.1
【解析】假设f(x0)=,则f(x)+=x0,进而f(x)=x0-,从而f(x0)=x0-+1)当x0=1时,f(1)=
因为f(x)是单调函数,所以由f(x0)=,可得x0=1,所以f(x)=1-
所以f(log22 019)=1-=,选C
6.等比数列{an}中,已知a1+a3=8,a5+a7=4,则a9+a11+a13+a15的值为( )
A.1 B.2 C.3 D.5
【解法1】设等比数列{an}的公比为q,则a5=a1q4,a7=a3q4,所以q4===
又a9+a11=a1q8+a3q8=(a1+a3)q8=8×2=2
a13+a15=a1q12+a3q12=(a1+a3)q12=8×3=1
所以a9+a11+a13+a15=2+1=3.
【解法2】因为{an}为等比数列,所以a5+a7是a1+a3与a9+a11的等比中项
所以(a5+a7)2=(a1+a3)(a9+a11),故a9+a11===2
同理,a9+a11是a5+a7与a13+a15的等比中项
所以(a9+a11)2=(a5+a7)(a13+a15),故a13+a15===1
所以a9+a11+a13+a15=2+1=3
7.已知f(x)=ax3+bx+1(ab≠0),若f(2 019)=k,则f(-2 019)=( )
A.k B.-k C.1-k D.2-k
【解析】∵f(2 019)=a·2 0193+b·2 019+1=k
∴a·2 0193+b·2 019=k-1,
则f(-2 019)=a(-2 019)3+b·(-2 019)+1=-[a·2 0193+b·2 019]+1=2-k
8.已知三点A(1,-2),B(a,-1),C(-b,0)共线,则+(a>0,b>0)的最小值为( )
A.11 B.10 C.6 D.4
【解析】由A(1,-2),B(a,-1),C(-b,0)共线得=,整理得2a+b=1
所以+=+=7++≥7+2=11
当且仅当=且2a+b=1即a=,b=时,等号成立,选A
方法11 分离参数法
9.已知函数f(x)=,若不等式f(x)≤kx对任意的x>0恒成立,则实数k的取值范围为________.
【解析】不等式f(x)≤kx对任意的x>0恒成立,即k≥对任意的x>0恒成立
令g(x)=,则g′(x)= =
令g′(x)=0,得x=,且当x∈(0,)时,g′(x)>0,当x∈(,+∞)时,g′(x)<0故当x=时,g(x)取得最大值g()==,所以k≥,即k的取值范围为
10.已知关于x的方程(t+1)cos x-tsin x=t+2在(0,π)上有实根,则实数t的最大值是________.
【解析】由题意可得:-==1-
如图,令P(cos x,sin x),A(2,1),则kPA=
因为x∈(0,π),所以-1<cos x<1,0<sin x≤1
令a=cos x,b=sin x,则点P是上半圆a2+b2=1(-1<a<1,0<b≤1)上任意一点
可知0≤kPA<1,所以0<1-≤1,即0<-≤1,所以t≤-1
故实数t的最大值是-1
11.已知函数f(x)=,ex) (a∈R).若?x∈[1,+∞),不等式f(x)>-1恒成立,求实数a的取值范围________
【解析】∵f(x)>-1?,ex)>-1?2a>x2-ex
∴由条件知,2a>x2-ex对于任意x≥1恒成立
令g(x)=x2-ex,h(x)=g′(x)=2x-ex
则h′(x)=2-ex
当x∈[1,+∞)时,h′(x)=2-ex≤2-e<0
∴h(x)=g′(x)=2x-ex在[1,+∞)上单调递减
∴h(x)=2x-ex≤2-e<0,即g′(x)<0
∴g(x)=x2-ex在[1,+∞)上单调递减
∴g(x)=x2-ex≤g(1)=1-e
故f(x)>-1在[1,+∞)上恒成立,只需2a>g(x)max=1-e
∴a>,故实数a的取值范围是
12.[2020·河南三市联考]已知函数f(x)=x-ln(x+1)对任意的x∈[0,+∞),都有f(x)≤kx2成立,则k的最小值为( )
A.1 B. C.e D.
【解法1】(一般解法)①当k≤0时,取x=1,有f(1)=1-ln 2>0,故k≤0不符合题意.
②当k>0时,令g(x)=f(x)-kx2,即g(x)=x-ln(x+1)-kx2,x≥0
所以g′(x)=1--2kx=-
令g′(x)=0,可得x1=0,x2=>-1
(ⅰ)当k≥时,≤0,g′(x)<0在(0,+∞)上恒成立,g(x)在[0,+∞)上单调递减
所以g(x)≤g(0)=0
所以对任意的x∈[0,+∞),有f(x)≤kx2成立
(ⅱ)当0
当0
因此存在x0∈使得g(x0)≥g(0)=0
可得x-ln(x0+1)≥kx,即f(x0)≥kx,与题设矛盾,该情况不成立
综上所述,当k≥时,对任意的x∈[0,+∞),都有f(x)≤kx2成立,则k的最小值为
选B
【解法2】(洛必达法则)当x=0时,不等式f(x)≤kx2显然成立
当x≠0时,不等式f(x)≤kx2恒成立可化为k≥=恒成立
因为f′(x)=1-≥0对任意的x∈[0,+∞)恒成立且f′(x)不恒为0
所以f(x)在[0,+∞)上也单调递增,而y=x2在[0,+∞)上单调递增,且其增速比f(x)大
易知满足使用洛必达法则的条件,则有 = = =
可得k≥,选B
方法12 估算法
13.[2020·山东济南部分学校联考]设a=,b=log35,c=log45,则a,b,c的大小关系是( )
A.a<b<c B.a<c<b C.b<c<a D.c<b<a
【解析】因为a=<1,b=log35>c=log45>1,所以a<c<b,选B
14.[2020·济南市高考模拟考试]如图,在多面体ABCDEF中,已知平面ABCD是边长为3的正方形,EF∥AB,EF=,EF与平面ABCD的距离为2,则该多面体的体积为( )
A. B.5 C.6 D.
【解析】连接BE,CE,四棱锥E ? ABCD的体积为VE ? ABCD=×3×3×2=6,
又多面体ABCDEF的体积大于四棱锥E ? ABCD的体积,
即所求几何体的体积V>VE ? ABCD=6,而四个选项里面大于6的只有,选D
15.设A,B,C,D是一个半径为4的球的球面上不共面的四点,△ABC为等边三角形且面积为9,则三棱锥D ? ABC的体积的最大值为( )
A.12 B.18 C.24 D.54
【解法1】由△ABC为等边三角形且面积为9,可得×AB2=9,解得AB=6
设球的球心为O,三角形ABC的外心为O′
则O′C==2,OO′==2,所以三棱锥D?ABC的高的最大值为6
则三棱锥D ?ABC的体积的最大值为××63=18,选B
【解法2】因为球的半径为4
三棱锥D?ABC的体积VD ? ABC=×9h=3h(h为点D到底面三角形ABC的距离,0
当h=4时,三角形ABC的外接圆半径为4,则△ABC的面积显然大于9,故可排除A
选B
方法13 函数方程思想
1.[2020·广东揭阳摸底]已知等差数列{an}的前n项和Sn满足S4=5,S9=20,则a7等于( )
A.-3 B.-5 C.3 D.5
【解法1】S9-S4=a5+a6+a7+a8+a9=15,所以5a7=15,所以a7=3.故选C
【解法2】设公差为d,由题意4a1+6d=5,9a1+36d=20,解得a1=,d=,所以a7=3
选C
2.将一个底面半径为1,高为2的圆锥形工件切割成一个圆柱体,能切割出的圆柱的最大体积为( )
A. B. C. D.
【解析】如图所示,设圆柱的半径为r,高为x,体积为V,
由题意可得=,所以x=2-2r,所以圆柱的体积V=πr2(2-2r)=2π(r2-r3)(0
所以圆柱的最大体积Vmax=2π=
3.[2020·陕西西安二模]已知函数f(x)=x2+4x+4,若存在实数t,当x∈[1,t]时,f(x-a)≤4x(a>0)恒成立,则实数t的最大值是( )
A.4 B.7 C.8 D.9
【解析】作函数f(x)=x2+4x+4=(x+2)2的简图如图所示.由图象可知
当函数y=f(x-a)的图象经过点(1,4)时
有x∈[1,t],f(x-a)≤4x(a>0)恒成立
此时t取最大值,由(1-a)2+4(1-a)+4=4,得a=5或a=1(舍),所以4t=(t-5+2)2
所以t=1(舍)或t=9,故t=9
4.[2018·全国卷Ⅰ]△ABC的内角A,B,C的对边分别为a,b,c.已知bsin C+csin B=4asin Bsin C,b2+c2-a2=8,则△ABC的面积为________.
【解析】∵ bsin C+csin B=4asin Bsin C
∴ 由正弦定理得sin Bsin C+sin Csin B=4sin Asin Bsin C
又sin Bsin C >0,∴ sin A=,由余弦定理得cos A===>0
∴ cos A=,bc==
∴ S△ABC=bcsin A=××=
5.[2020·山东青岛期中联考]已知函数f(x)=x2-2ax+b(a>1)的定义域和值域都为[1,a],则b=________.
【解析】函数f(x)=x2-2ax+b(a>1)图象的对称轴方程为x=-=a>1,
所以函数f(x)=x2-2ax+b在[1,a]上为减函数,
又函数在[1,a]上的值域也为[1,a],∴即
由①得b=3a-1,代入②得a2-3a+2=0,解得a=1(舍)或a=2.
把a=2代入b=3a-1得b=5
6.已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),P是双曲线C右支上一点,且|PF2|=|F1F2|,若直线PF1与圆x2+y2=a2相切,则双曲线的离心率为________.
【解析】取线段PF1的中点为A,连接AF2,又|PF2|=|F1F2|,则AF2⊥PF1,
∵直线PF1与圆x2+y2=a2相切,∴|AF2|=2a,
∵|PA|=|PF1|=a+c,∴4c2=(a+c)2+4a2,化简得(3c-5a)(a+c)=0,
则双曲线的离心率为
7.已知函数f(x)=lg,其中a为常数,若当x∈(-∞,1],f(x)有意义,则实数a的取值范围为________
【解析】由>0,且a2-a+1=2+>0
得1+2x+4x·a>0,故a>-
当x∈(-∞,1]时,y=与y=都是减函数
因此,函数y=-在(-∞,1]上是增函数
所以max=-,所以a>-
故实数a的取值范围是
8.关于x的不等式ex--1-x≥0在x∈上恰成立,则a的取值集合为________.
【解析】关于x的不等式ex--1-x≥0在x∈上恰成立?函数g(x)=在上的值域为
因为g′(x)=
令φ(x)=ex(x-1)-x2+1,x∈,则φ′(x)=x(ex-1)
因为x≥,所以φ′(x)≥0,故φ(x)在上递增,所以φ(x)≥φ=->0
因此g′(x)>0,故g(x)在上单调递增
则g(x)≥g==2-,所以a-=2-,解得a=2
所以a的取值集合为{2}
9.[2020·江苏扬州大学附中月考]已知二次函数g(x)=mx2-2mx+n+1(m>0)在区间[0,3]上有最大值4,最小值0.求函数g(x)的解析式
【解析】g(x)=mx2-2mx+n+1(m>0),易知g(x)图象开口向上,对称轴方程为x=1
∵x∈[0,3],∴当x=1时,g(x)取得最小值-m+n+1=0,①
当x=3时,g(x)取得最大值3m+n+1=4,②
由①②解得m=1,n=0
∴函数g(x)的解析式为g(x)=x2-2x+1
10.[2018·全国卷Ⅱ节选]设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A,B两点,|AB|=8.求l的方程
【解析】由题意得F(1,0),l的方程为y=k(x-1)(k>0)
设A(,),B(,)
由得k2x2-(2k2+4)x+k2=0
Δ=16k2+16>0,故+=
所以|AB|=|AF|+|BF|=(+1)+(+1)=
由题设知=8,解得k=-1(舍去)或k=1
因此l的方程为y=x-1
方法14 数形结合思想
1.[2020·福建省质量检测]在△ABC中,=2,且E为AC的中点,则=( )
A.-+ B.- C.-- D.+
【解法1】如图1,连接AD
=-=-(+)=--(-)=-+.
【解法2】=++=-+=(+)-+=-+.
【解法3】如图2,作=,以,为基底将分解,=+=x+y,则=x+y,易知x<0,y>0,排除B,C,D选项,故选A.
【解法4】不妨令△ABC为直角三角形,C=90°,AC=2,BC=3,以C为坐标原点建立直角坐标系,如图3所示,则C(0,0),A(2,0),B(0,3),D(0,2),E(1,0),
所以=(-2,3),=(-2,0),=(1,-2),易得=-+,选A
2.[2020·广东省联考试题]函数f(x)=的部分图象大致是( )
【解析】因为f(-x)==-f(x)
所以f(x)为奇函数,其图象关于原点对称
当x∈(0,1)时,f(x)=<0
当x∈(1,+∞)时,f(x)>0
选D
3.设双曲线C: -=1(a>0,b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,以F1F2为直径的圆与双曲线左支的一个交点为P.若以A1A2为直径的圆与直线PF2相切,则双曲线C的离心率为( )
A. B. C.2 D.
【解析】如图所示,设以A1A2为直径的圆与直线PF2的切点为Q,连接OQ,则OQ⊥PF2,
又PF1⊥PF2,O为F1F2的中点
所以|PF1|=2|OQ|=2a
又|PF2|-|PF1|=2a
所以|PF2|=4a
在Rt△F1PF2中,|PF1|2+|PF2|2=|F1F2|2?4a2+16a2=20a2=4c2?e==
4.[2020·郑州市质量预测]已知函数f(x)=sin的相邻两条对称轴之间的距离为,将函数f(x)的图象向右平移个单位后,再将所有点的横坐标伸长为原来的2倍,得到g(x)的图象,若g(x)+k=0在x∈有且只有一个实数根,则k的取值范围是( )
A.k≤ B.-1≤k<- C.-
结合三角函数的图象可知=
又因为T===
所以ω=2,f(x)=sin
将f(x)的图象向右平移个单位得到f(x)=sin=sin,再将所有点的横坐标伸长为原来的2倍得到g(x)=sin,所以方程为sin+k=0
令2x-=t,因为x∈
所以-≤t≤
若g(x)+k=0在x∈上有且只有一个实数根
即g(t)=sin t与y=-k在上有且只有一个交点
-≤-k<或-k=1
即-
A.[-1,0) B.[0,+∞) C.[-1,+∞) D.[1,+∞)
【解析】令h(x)=-x-a,则g(x)=f(x)-h(x)
在同一坐标系中画出y=f(x),y=h(x)图象的示意图,如图所示
若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象
当直线y=-x-a过点(0,1)时,有2个交点,
此时1=-0-a,a=-1.
当y=-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意
当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意
综上,a的取值范围为[-1,+∞),选C
6.[2020·合肥市高三调研性检测]若实数x,y满足约束条件则z=2x-y的最大值为________.
【解析1】依题意,在坐标平面内画出不等式组表示的平面区域,如图中阴影部分所示,作出直线2x-y=0,平移该直线,当平移到经过点A(3,-2)时,相应直线在y轴上的截距达到最小,此时z=2x-y取得最大值,即zmax=2×3-(-2)=8
【解析2】由得
此时z=8;由得
此时z=4;由得,此时z=-1
综上所述,z=2x-y最大值为8.
7.[2020·武汉市调研测试]过圆O:x2+y2=4外一点P(2,1)作两条互相垂直的直线AB和CD分别交圆O于A,B和C,D点,则四边形ABCD面积的最大值为________.
【解析】如图所示,S四边形ABCD=(PA·PD-PB·PC),取AB,CD的中点分别为E,F,连接OE,OF,OP,
则S四边形ABCD=[(PE+AE)·(PF+DF)-(PE-AE)·(PF-DF)]=PE·DF+AE·PF
由题意知四边形OEPF为矩形,则OE=PF,OF=PE
结合柯西不等式有S四边形ABCD=OF·DF+AE·OE≤
其中OF2+OE2=OP2,DF2+AE2=4-OF2+4-OE2=8-OP2
据此可得S四边形ABCD≤==
综上,四边形ABCD面积的最大值为.
8.[2020·开封市高三模拟试卷]已知函数f(x)是定义域为R的奇函数,满足f(x)+f(2-x)=0,且当x∈(0,1)时,f(x)=x2,则f(1)=________,g(x)=f(x)-|lg x|,则函数g(x)的零点共有______个.
【解析】因为f(x)是定义在R上的奇函数,所以f(0)=0,
因为f(x)+f(2-x)=0,
所以令x=1得f(1)+f(1)=0,即f(1)=0.
由f(x)+f(2-x)=0得f(x)=-f(2-x),
又f(x)是奇函数,
所以-f(2-x)=f(x-2),
即f(x)=f(x-2),
则f(x)是以2为周期的周期函数,
则f(0)=f(2)=0,f(1)=f(3)=0,
即f(n)=0(n∈Z).
注意到f(x)的值域为(-1,1),
由g(x)=0得f(x)=|lg x|<1,
在同一平面直角坐标系内作出函数y=f(x)与y=|lg x|的图象,如图所示,
由图可知,y=f(x)的图象与函数y=|lg x|的图象共有6个交点
因此函数g(x)的零点共有6个
9.已知函数f(x)=2sin2+cos 2x.
(1)求函数f(x)的单调递增区间;
(2)若关于x的方程f(x)-m=2在x∈上有两个不同的解,求实数m取值范围.
【解析】(1)由f(x)=2sin2+cos 2x
=1-cos+cos 2x
=1+sin 2x+cos 2x
=1+2sin,
则由2kπ-≤2x+≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z.
所以函数的单调递增区间为,k∈Z.
(2)
由f(x)-m=2,得f(x)=m+2,
当x∈时,2x+∈,
∵f(0)=1+2sin=1+,函数f(x)的最大值为1+2=3,
∴要使方程f(x)-m=2在x∈上有两个不同的解,则f(x)=m+2在x∈上有两个不同的解,即f(x)和y=m+2在x∈上有两个不同的交点,即1+≤m+2<3
即-1≤m<1.
所以实数m的取值范围为[-1,1).
10.[2020·武汉市质量检测]如图,在棱长为a的正方体ABCD ? A1B1C1D1中,P,Q,L分别为棱A1D1,C1D1,BC的中点.
(1)求证:AC⊥QL;
(2)求点A到平面PQL的距离.
【解析】(1)如图,取DC的中点H,连接QH,HL,BD.在正方体ABCD ? A1B1C1D1中,H,Q分别为DC,C1D1的中点,则QH⊥CD,从而QH⊥平面ABCD,所以QH⊥AC.
在正方形ABCD中,H,L分别为CD,BC的中点,所以BD∥HL,又AC⊥BD,
所以HL⊥AC
又QH∩HL=H,所以AC⊥平面QHL,所以AC⊥QL
(2)取AB的中点M,连接ML,MP,因为M,L分别为AB,BC的中点,所以ML∥AC
又AC⊥QL,所以ML⊥QL,易证PQ∥ML且PQ=ML,所以四边形PQLM为矩形
则点A到平面PQL的距离即点A到平面PML的距离,设其值为h
连接PA,AL,在四面体PAML中,S△AML=AM·BL=··=a2,
S△PML=·ML·PM=·a·=a2
由等体积法可知V三棱锥P ? AML=V三棱锥A ? PML,即·a2·a=·a2·h,解得h=a
故点A到平面PQL的距离为a
方法15 分类讨论思想
1.[2020·开封市高三模拟试卷]设常数a∈R,集合A={x|(x-1)(x-a)≥0},B={x|x≥a-1},若A∪B=R,则a的取值范围为
【解析】若a>1,集合A={x|x≤1或x≥a},
利用数轴可知,要使A∪B=R,需a-1≤1,解得1
若a<1,集合A={x|x≤a或x≥1},利用数轴可知,显然满足A∪B=R,故a<1符合题意.
综上,a的取值范围为(-∞,2]
2.已知a>0,b>0,且a≠1,b≠1,若logab>1,则( )
A.(a-1)(b-1)<0 B.(a-1)(a-b)>0 C.(b-1)(b-a)<0 D.(b-1)(b-a)>0
【解析】∵a>0,b>0,且a≠1,b≠1
∴当a>1,即a-1>0时,不等式logab>1可化为alogab>a1,即b>a>1
∴(a-1)(a-b)<0,(a-1)(b-1)>0,(b-1)(b-a)>0
当0
综上可知,选D
3.若双曲线+=1的渐近线方程为y=±x,则m的值
【解析】根据题意可分以下两种情况讨论:
①当焦点在x轴上时,则有解得m<1
此时渐近线方程为y=± x,由题意得,=,解得m=
②当焦点在y轴上时,则有解得m>3
此时渐近线方程为y=± x,由题意得,=,无解
综上可知m=
4.[2020·湖北武汉调研]已知实数x,y满足约束条件如果目标函数z=x+ay的最大值为,则实数a的值为( )
A.3 B. C.3或 D.3或-
【解析】先画出线性约束条件所表示的可行域,目标函数化为y=-x+z,目标函数z=x+ay的最大值只需直线的截距最大,
当a>0时,-<0,
①若-<-<0,即a>2,最优解为A,
z=+a=,a=3,符合题意;
②若-<-,即0
当a<0时,->0,
③若0<-<1,即a<-1,最优解为C(-2,-2),
z=-2-2a=,a=-,符合题意;
④若->1,即-1
综上可知实数a的值为3或-.故选D.
5.[2020·江西师范附属中学模拟]已知f(x)=,若f(2-a)=1,则f(a)等于( )
A.-2 B.-1 C.1 D.2
【解析】①当2-a≥2,即a≤0时,22-a-2-1=1,解得a=-1
则f(a)=f(-1)=-log2[3-(-1)]=-2
②当2-a<2即a>0时,-log2[3-(2-a)]=1
解得a=-,舍去
所以f(a)=-2.故选A
6.[2020·安徽阜阳二模]等比数列{an}中,a1+a4+a7=2,a3+a6+a9=18,则{an}的前9项和S9=________
【解析】由题意得q2==9,q=±3
①当q=3时,a2+a5+a8=3(a1+a4+a7)=6,S9=2+6+18=26
②当q=-3时,a2+a5+a8=-3(a1+a4+a7)=-6,S9=2-6+18=14
所以S9=14或26
7.设圆锥曲线Γ的两个焦点分别为F1,F2.若曲线Γ上存在点P满足|PF1|:|F1F2|:|PF2|=4:3:2,则曲线Γ的离心率等于________
【解析】设|F1F2|=2c(c>0)
由已知|PF1|︰|F1F2|︰|PF2|=4︰3︰2
得|PF1|=c,|PF2|=c,且|PF1|>|PF2|
若圆锥曲线Γ为椭圆,则2a=|PF1|+|PF2|=4c,离心率e=
若圆锥曲线Γ为双曲线,则2a=|PF1|-|PF2|=c,离心率e=
故曲线Γ的离心率等于或
8.f(x)是定义在R上的函数,满足f(x)=f(-x),且x≥0时,f(x)=x3,若对任意的x∈[2t-1,2t+3],不等式f(3x-t)≥8f(x)恒成立,则实数t的取值范围是________.
【解析】f(x)是定义在R上的偶函数,f(x)=x3,在x>0上为单调增函数,
f(3x-t)≥8f(x)=8x3=f(2x),
|3x-t|≥|2x|,所以(3x-t)2≥(2x)2,化简得5x2-6xt+t2≥0.(*)
①当t=0时显然成立;
②当t>0时,(*)式解为x≤或x≥t,对任意x∈[2t-1,2t+3],(*)式恒成立,则需t≤2t-1,故t≥1;
③当t<0时,(*)式解为x≤t或t≥,对任意x∈[2t-1,2t+3],
(*)式恒成立,则需2t+3≤t,故t≤-3.
综上所述,t≤-3或t≥1或t=0.
9.已知a,b,c分别是△ABC的内角A,B,C所对的边,a=2bcos B,b≠c.
(1)证明:A=2B;
(2)若a2+c2=b2+2acsin C,求A.
【解析】(1)证明:∵a=2bcos B,且=,∴sin A=2sin Bcos B=sin 2B
∵0
若A+2B=π,则B=C,b=c,这与“b≠c”矛盾,∴A+2B≠π,∴A=2B
(2)∵a2+c2=b2+2,∴=sin C,由余弦定理得cos B=sin C
∵0
②当C=+B时,由(1)得A=2B,∴A+B+C=A+2B+=2A+=π,∴A=
综上,A=
10.[2020·河南省豫北名校高三质量考评]已知函数f(x)=2ax-aex-1(a≠0).
(1)求函数f(x)的单调区间;
(2)若f(x)≤e-2-(a+1)ex对任意x∈[1,2]恒成立,求实数a的取值范围.
【解析】(1)由题意得f′(x)=2a-aex=a(2-ex).
令f′(x)=0,得x=ln 2.
当a>0时,由f′(x)>0,得x
所以f(x)的单调递增区间为(-∞,ln 2),单调递减区间为(ln 2,+∞);
当a<0时,则易得f(x)的单调递增区间为(ln 2,+∞),单调递减区间为(-∞,ln 2).
(2)f(x)≤e-2-(a+1)ex(a≠0)对任意x∈[1,2]恒成立,即2ax-aex-1≤e-2-(a+1)ex(a≠0)对任意x∈[1,2]恒成立,即2ax+ex+1-e≤0(a≠0)对任意x∈[1,2]恒成立.
令F(x)=2ax+ex+1-e(a≠0),则F′(x)=2a+ex(a≠0),
当a>0时,F′(x)=2a+ex>0,F(x)在[1,2]上单调递增,
F(1)=2a+1>0,F(x)≤0在[1,2]上不成立,不满足题意.
当a<0时,由F′(x)=0,得x=ln(-2a),当x∈(-∞,ln(-2a))时F′(x)<0,F(x)单调递减;当x∈(ln(-2a),+∞)时,F′(x)>0,F(x)单调递增.
若ln(-2a)≤1,即-≤a<0,则F(x)在[1,2]上单调递增,
由F(2)=4a+e2-e+1≤0,得a≤,又-≤a<0,所以不存在满足题意的a.
若1
由F(1)=2a+1≤0,得a≤-,由F(2)=4a+e2-e+1≤0,得a≤,
又-
由F(1)=2a+1≤0,得a≤-,又a≤-,所以a≤-.
综上所述,a的取值范围为
方法16 转化化归思想
1.[2020·湖南衡阳联考]设正项等差数列{an}的前n项和为Sn,若S2 019=6 057,则+的最小值为( )
A.1 B. C. D.
【解析】依题意得(a1+a2 019)=6 057?a1+a2 019=a2+a2 018=6,
+=(a2+a2 018)=≥,仅当a2=2,a2 018=4时取等号
选D.
2.设f(x)是奇函数,对任意的实数x,y,有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,则f(x)在区间[a,b]上( )
A.有最小值f(a) B.有最大值f(a) C.有最大值f D.有最小值f
【解法1】因为f(x)是奇函数,且对任意的实数x,y,有f(x+y)=f(x)+f(y),
则f(0)=0,当x>0时,f(x)<0,则当x<0时,f(x)>0,
对任意x1,x2∈R,f(x+y)=f(x)+f(y),当x1
因为x1-x2<0,所以f(x1-x2)>0,即f(x1)-f(x2)>0,故f(x)在R上是减函数,故f(x)在区间[a,b]上有最大值f(a).故选B.
【解法2】f(x)=-x显然符合条件,易得f(x)=-x在区间[a,b]上有最大值f(a),选B
3.已知H为△ABC的垂心,AB=4,AC=6,M为边BC的中点,则·=( )
A.20 B.10 C.-20 D.-10
【解法1】如图所示,因为H为△ABC的垂心,
所以⊥,所以·=0,
又AB=4,AC=6,且M为边BC的中点,
所以·=(++)·=·=·+·
=(+)·(-)=(2-2)=×(36-16)=10,选B
【解法2】将△ABC特殊化为直角三角形,建立如图所示的平面直角坐标系,根据AB=4,AC=6,得B(0,4),C(6,0),M(3,2),H(0,0),
所以·=(3,2)·(6,-4)=10.故选B.
4.[2020·南昌师大附中模拟]函数f(x)=ln x+x2-ax(x>0)在区间上有且仅有一个极值点,则实数a的取值范围是( )
A. B. C. D.
【解析】由f(x)=ln x+x2-ax(x>0)得f′(x)=+x-a(x>0).
因为函数f(x)=ln x+x2-ax在区间上有且仅有一个极值点,
所以y=f′(x)在区间上有且仅有一个变号零点.
令f′(x)=+x-a=0,得a=+x,令g(x)=+x,x∈,则g(x)在区间上单调递减,在区间(1,3]上单调递增,所以g(x)min=g(1)=2.
又g=g(2)=,g(3)=,结合函数g(x)=+x,x∈的图象(图略)可得,
当≤a<时,y=f′(x)在区间上有且仅有一个变号零点.
所以实数a的取值范围为,故选B.
5.若二次函数f(x)=4x2-2(p-2)x-2p2-p+1在区间[-1,1]内至少存在一个值c,使得f(c)>0,则实数p的取值范围是____________.
【解析】如果在[-1,1]内没有值满足f(c)>0,则?
?p≤-3或p≥,取补集为-3
6.对于满足0≤p≤4的所有实数p,使不等式x2+px>4x+p-3成立的x的取值范围是______.
【解析】设f(p)=(x-1)p+x2-4x+3,则当x=1时,f(p)=0,所以x≠1.
f(p)在0≤p≤4上恒为正,等价于即解得x>3或x<-1
7.[2020·郑州市质检]函数f(x)=x3+3ax-1,g(x)=f′(x)-ax-5,其中f′(x)是f(x)的导函数.对满足-1≤a≤1的一切a的值,都有g(x)<0,则实数x的取值范围为________.
【解析】由题意,知g(x)=3x2-ax+3a-5,
令φ(a)=(3-x)a+3x2-5,-1≤a≤1.
对-1≤a≤1,恒有g(x)<0,即φ(a)<0,
所以即解得-
8.[2020·南京模拟]若函数f(x)=-ln(x+1)不存在零点,则实数k的范围是_______
【解析】由x+1>0得x>-1,由kx>0得
当=ln(x+1)时,由对数的性质可得ln(kx)=2ln(x+1)=ln(x+1)2,
即kx=(x+1)2,变形可得k==x++2(x>-1且x≠0),
易知当-1
要使函数f(x)=-ln(x+1)不存在零点,
只需k取x++2(x>-1且x≠0)的取值集合的补集,即{k|0≤k<4},
当k=0时,函数无意义,故k的取值范围是(0,4).
9.若对于任意t∈[1,2],函数g(x)=x3+x2-2x在区间(t,3)上总不为单调函数,求实数m的取值范围
【解析】g′(x)=3x2+(m+4)x-2
若g(x)在区间(t,3)上总为单调函数
则①g′(x)≥0在(t,3)上恒成立,或②g′(x)≤0在(t,3)上恒成立.(正反转化)
由①得3x2+(m+4)x-2≥0,即m+4≥-3x
当x∈(t,3)时恒成立,∴m+4≥-3t恒成立
则m+4≥-1,即m≥-5
由②得3x2+(m+4)x-2≤0,即m+4≤-3x
当x∈(t,3)时恒成立
则m+4≤-9,即m≤-
∴函数g(x)在区间(t,3)上总不为单调函数的m的取值范围为
10.[2020·开封市高三模拟试卷]如图,点O为长方形ABCD的中心,EC⊥平面ABCD,BC=2CD=2,EC=2,M是线段ED上不同于E的动点,N是线段AC上的动点.
(1)求证:平面ABE⊥平面CBE;(2)求二面角M ? BE ? N的取值范围.
【解析】(1)EC⊥平面ABCD,AB?平面ABCD,所以EC⊥AB,
长方形ABCD中,CB⊥AB,又EC∩CB=C,所以AB⊥平面CBE,
又AB?平面ABE,所以平面ABE⊥平面CBE.
(2)以C为坐标原点,的方向为x轴正方向,|C|为单位长度,建立如图所示的空间直角坐标系C?xyz,连接BD,则AC与BD交于点O,连接OE,
半平面BEM即半平面BED,C(0,0,0),D(1,0,0),O,B(0,2,0),E(0,0,2)
因为AB⊥平面CBE,所以CD⊥平面CBE,所以平面CBE的一个法向量为=(1,0,0),
设平面BEO的法向量为m=(x,y,z),又=,=(0,-2,2),
所以,即,令z=1,则m=(2,,1),
所以cos〈,m〉==,二面角O ? BE ? C的大小为.
又由(1)可知,二面角C ? BE ? A的大小为,所以二面角O ? BE ? A的大小为,当N位于点O时,二面角M ? BE ? N的大小为0,所以二面角M ?BE?N的取值范围是
同课章节目录
