2021届高三三轮回归专练——计数原理涉及的11类错解及10大解题模板汇编
文档属性
| 名称 | 2021届高三三轮回归专练——计数原理涉及的11类错解及10大解题模板汇编 |

|
|
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览




文档简介
计数原理排列组合中常见11类错误题型
(一)至少问题
某班有20名女生和19名男生,从中选出5人组成一个垃圾分类宣传小组,要求女生和男生均不少于2人的选法共有( )
A. B.
C. D.
【解析】从中选出5人组成一个垃圾分类宣传小组,要求女生和男生均不少于2人
当选出5人为2女3男时,共有不同选法为种,当选出5人为3女2男时,共有不同选法为种
即选出5人组成一个垃圾分类宣传小组,要求女生和男生均不少于2人选法有种,选D
假设200件产品中有3件次品,现在从中任取5件,其中至少有2件次品的抽法有( )
A.种 B.种
C.种 D.种
【解析】根据题意,“至少有2件次品”可分为“有2件次品”与“有3件次品”两种情况
“有2件次品”的抽取方法有C32C1973种,“有3件次品”的抽取方法有C33C1972种
则共有C32C1973+C33C1972种不同的抽取方法,故选B
(二)不相邻问题插空法
有红色、黄色小球各两个,蓝色小球一个,所有小球彼此不同,现将五球排成一行,颜色相同者不相邻,不同的排法共有( )种
A.48 B.72 C.78 D.84
【解析】五个小球全排列共有:种排法
当两个红色小球与两个黄色小球都相邻时,共有:种排法
当两个红色小球相邻,两个黄色小球不相邻时,共有:种排法
当两个红色小球不相邻,两个黄色小球相邻时,共有:种排法
颜色相同的小球不相邻的排法共有:种排法,选
7人并排站成一行,如果甲、乙两人不相邻,那么不同的排法总数是
A.1440 B.3600 C.4320 D.4800
【解析】除甲、乙以外的5人全排列,共有种结果,5人排队后会出现6个空,从中选出2个排甲、乙,有种结果。所以满足条件的排队总数=(种),故选B
(三)相邻问题大元素法
2位男生和3位女生共5位同学站成一排,若3位女生中有且只有两位女生相邻,则不同排法的种数是
A.36 B.24 C.72 D.144
【解析】根据题意,把3位女生的两位捆绑在一起看做一个复合元素,和剩下的一位女生,
插入到2位男生全排列后形成的3个空中的2个空中,故有种,选.
2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5 B.21元 C.21.5元 D.22元
【解析】捆绑法求得照片总数为,每名老党员需要支付照片费为元
(四)分配问题
高三年级有8个班级,分派4位数学老师任教,每个教师教两个班,则不同的分派方法有( )
A. B. C. D.
【解析】分两步,第一步将高三8个班级,两两一组分4组,共有种分法,第二步将4位数学老师分配到这4组,共有种情况,所以不同的分派方法有=,选B
将3名教师,5名学生分成3个小组,分别安排到甲、乙、丙三地参加社会实践活动,每地至少去1名教师和1名学生,则不同的安排方法总数为( )
A.1800 B.1440 C.300 D.900
【解析】先将3名教师安排到甲、乙、丙三地有种分法
然后安排5名学生,将5名学生可分为1,1,3三组,也可分为2,2,1三组
则安排到三地有种方法
根据分步乘法原理,可知不同的安排方法总数为种,故选D.
(五)特殊元素优先
10名运动员中有2名老队员和8名新队员,现从中选3人参加团体比赛,要求老队员至多1人入选且新队员甲不能入选的选法有( )
A.77种 B.144种 C.35种 D.72种
【解析】按照老队员的人数分两类:
(1)只选一名老队员,则新队员选2名(不含甲)有42
(2)没有选老队员,则选3名新队员(不含甲)有
所以老队员至多1人入选且新队员甲不能入选的选法有:种,故选A
中国古代儒家要求学生掌握六种基本才能(六艺):礼、乐、射、御、书、数。某校国学社团周末开展“六艺”课程讲座活动,一天连排六节,每艺一节,排课有如下要求:“射”不能排在第一,“数”不能排在最后,则“六艺”讲座不同的排课顺序共有______种.
【解析】第一种情况,当“射”排最后一位时,共有种方法
第二种情况,当“射”排中间4个位置中的1个时共有种方法
不同的排列方式共有种
所以“六艺”讲座不同的排课顺序共有504种
2位男生和3位女生共5位同学站成一排,若3位女生中有且只有两位女生相邻,则不同排法的种数是
A.36 B.24 C.72 D.144
【解析】根据题意,把3位女生的两位捆绑在一起看做一个复合元素,和剩下的一位女生,
插入到2位男生全排列后形成的3个空中的2个空中,故有种,选
(六)涂色问题
如图,用5种不同的颜色把图中、、、四块区域分开,若相邻区域不能涂同一种颜色,则不同的涂法共有( )
A.200种 B.160种 C.240种 D.180种
【解析】涂有5种涂法,有4种,有3种,因为可与同色,故有3种,
∴由分步乘法计数原理知,不同涂法有种.故答案选D。
如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )
A.120种 B.240种 C.144种 D.288种
【解析】不考虑红色的位置,黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案有种. 这种情况下,红色在左右两端的涂色方案有种;从而所求的结果为种,故选D.
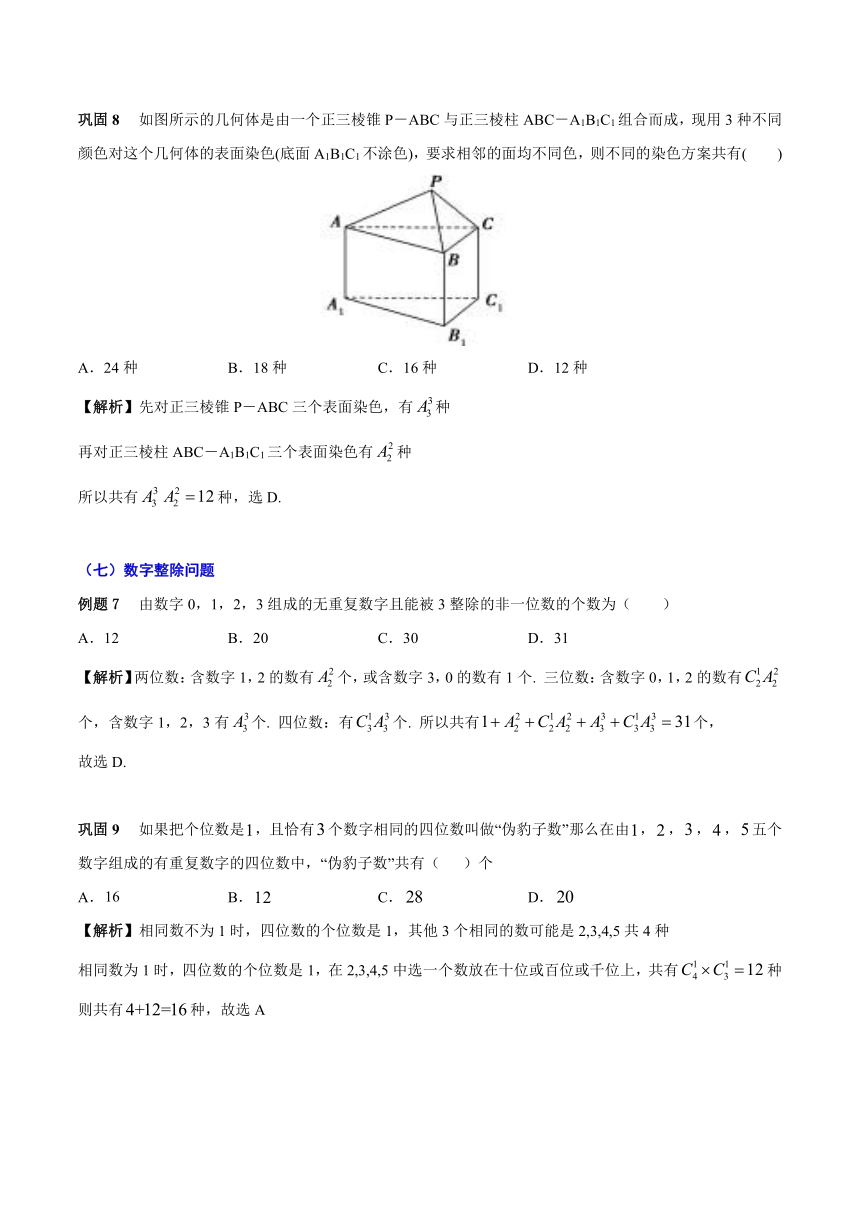
如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
A.24种 B.18种 C.16种 D.12种
【解析】先对正三棱锥P-ABC三个表面染色,有种
再对正三棱柱ABC-A1B1C1三个表面染色有种
所以共有种,选D.
(七)数字整除问题
由数字0,1,2,3组成的无重复数字且能被3整除的非一位数的个数为( )
A.12 B.20 C.30 D.31
【解析】两位数:含数字1,2的数有个,或含数字3,0的数有1个. 三位数:含数字0,1,2的数有个,含数字1,2,3有个. 四位数:有个. 所以共有个,
故选D.
如果把个位数是,且恰有个数字相同的四位数叫做“伪豹子数”那么在由,,,,五个数字组成的有重复数字的四位数中,“伪豹子数”共有( )个
A. B. C. D.
【解析】相同数不为1时,四位数的个位数是1,其他3个相同的数可能是2,3,4,5共4种
相同数为1时,四位数的个位数是1,在2,3,4,5中选一个数放在十位或百位或千位上,共有种
则共有种,故选A
(八)正难则反
某电商为某次活动设计了“和谐”、“爱国”、“敬业”三种红包,活动规定每人可以依次点击4次,每次都会获得三种红包的一种,若集全三种即可获奖,但三种红包出现的顺序不同对应的奖次也不同员工甲按规定依次点击了4次,直到第4次才获奖则他获得奖次的不同情形种数为
A.9 B.12 C.18 D.24
【解析】根据题意,若员工甲直到第4次才获奖,则其第4次才集全“和谐”、“爱国”、“敬业”三种红包
则甲第4次获得的红包有3种情况
前三次获得的红包为其余的2种,有种情况
则他获得奖次的不同情形种数为种,选C
把20个相同的小球装入编号分别为①②③④的4个盒子里,要求①②号盒每盒至少3个球,③④号盒每盒至少4个球,共有( )种方法.
A. B. C. D.
【解析】设四个盒子中装的小球个数分别为,,,,则
要求①②号盒每盒至少3个球,③④号盒每盒至少4个球
令,,,,则,,,都大于或等于1,且
问题相当于将10个球分成四部分,在10个球的9个间隔里选三个隔开,有种方法,选A
(九)避免出错---彻底分类
今有个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有( )种
A. B. C. D.
【解析】第一类:只用两辆缆车,
若两个小孩坐在一块,则有种乘车方式;
若两个小孩不坐在一块,则有种乘车方式
第二类:用三辆缆车
若两个小孩坐在一块,则有种乘车方式
若两个小孩不坐在一块,则有种乘车方式
综上不同的乘车方式有种,故选C
某学校要安排2名高二的同学,2名高一的同学和名初三的同学去参加电视节目《变形记》,有五个乡村小镇A、B、C、D,E(每名同学选择一个小镇)由于某种原因高二的同学不去小镇A,高一的同学不去小镇B,初三的同学不去小镇D和E,则共有________种不同的安排方法(用数字作)
【解析】如果初三学生去,则高二学生选人去,另外三人去,故方法数有种
如果初三学生去,则高一学生选人去,另外三人去,故方法数有种
如果初三学生去,则高二学生选人去,高一学生选人去,另外两人去,有种
故总的方法数有种
(十)空间几何体与排列组合
已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为
A.40 B.16 C.13 D.10
【解析】分两类情况讨论:第1类,直线a分别与直线b上的8个点可以确定8个不同的平面;第2类,直线b分别与直线a上的5个点可以确定5个不同的平面.
根据分类加法计数原理知,共可以确定8+5=13个不同的平面,故选C.
在一个质地均匀的四面体中,一个面上标有数字1,一个面上标有数字2,另外有两个面上标有数字3,将该正四面体抛掷三次,则向下一面的数字之和为7的情况有________种
【解析】因为四面体中,一个面上标有数字1,一个面上标有数字2,另外有两个面上标有数字3,当将该正四面体抛掷三次,则向下一面的数字之和为7的情况有两类:
当组合为2,2,3时,可能有种情况
当组合为1,3,3时,可能有种情况
综上可知,所有出现向下一面的数字之和为7的情况有种
(十一)排列组合综合问题
空间中不共面的4点A,B,C,D,若其中3点到平面的距离相等且为第四个点到平面的2倍,这样的平面的个数为( )
A.8 B.16 C.32 D.48
【解析】第一种情况,A,B,C,D点在平面的同侧.
当平面∥平面BCD时,A与平面的距离是与平面BCD的距离的2倍.
这种情况下有4个平面.
第二种情况,A,B,C,D中有3个点在平面的一侧,第4个点在平面的另一侧,这时又有两种情形:
一种情形是平面与平面BCD平行,且A与平面距离是平面与平面BCD距离的2倍.这时有4个平面.
另一种情形如图a所示,图中E,F分别是AB,AC的中点,K是AD的三等分点中靠近A的分点,A,B,C到平面EFK(即平面)的距离是D到平面EFK距离的一半.
∵EF可以是AB,AC的中点的连线,又可以是AB,BC的中点的连线,或AC,BC的中点的连线,
∴这种情形下的平面有3×4=12(个).
第三种情况,如图b所示,在A,B,C,D四点中,平面两侧各种有两点.
容易看出:点A到平面EFMN(平面)的距离是B,C,D到该平面距离的2倍。
就A,C与B,D分别位于平面两侧的情形来看,就有A离平面远,B离平面远,C离平面远,D离平面远这四种情况.
又“AC,BD异面,则这样的异面直线共有3对
∴平面有4×3=12(个).
综上分析,平面有4+4+12+12=32(个),选C
若矩阵满足下列条件:①每行中的四个数均为集合{1,2,3,4}中不同元素;②四列中有且只有两列的上下两数是相同的,则满足①②条件的矩阵的个数为( )
A.48 B.72 C.144 D.264
【解析】第一步,排列第一行,有种排列方法;
第二步,由题意知有且只有两列的上下两数是相同的,选择中的两个数作为与上列相同的数字,有种取法,而对于剩余两数,为使不与上列数字相同,有且只有一种排法,
因此,满足题中条件的矩阵的个数共有个,故选C.
如图,平面中有梯形与梯形分别在直线的两侧,它们与无公共点,并且关于成轴对称,现将沿折成一个直二面角,则,,,,,,,八个点可以确定平面的个数是( )
A.56 B.44 C.32 D.16
【解析】由题设从八个顶点中任取三个确定的所有平面的个数个,其中六个平面中任取三个点所确定的平面个数为个,故,,,,,,,八个点可以确定平面的个数是,选C
中国古代儒家要求学生掌握六种基本才能:礼、乐、射、御、书、数.“礼”,礼节,即今德育:“乐”,音乐,“射”和“御”,射箭和驾驭马车的技术,即今体育和劳动:“书”,书法,即今文学;“数”,算法,即今数学。某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”必须排在第一,“数”不能排在最后,“射”和“御”要相邻,则“六艺”讲座不同的排课顺序共有( )
A.种 B.种 C.种 D.种
【解析】如果“射”或“御”排在最后,那么“射”和“御”有两种排法即种,余下3种才能共有种排法,故此时共有中排法;
如果“射”和“御”均不在最后,那么“射”和“御”有种排法,中间还余两个位置,两个位置可选一个给“数”,有2种排法,余下两个位置放置最后的两个基本才能,有,故共有种排法,
综上,共有36种排法,选B.
已知数列,.满足条件“”的数列个数为_____.
【解析】因为,所以只能取0或1
而
所以中出现0的个数可以是6个,5个,4个,3个。
若出现6个0,则数列为常数数列,共有1个数列。
若出现5个0,则出现一个1,或一个,因而数列个数为个数列。
若出现4个0,出现两个1,或两个,或一个1、一个,数列个数为个数列
若出现3个0,则出现三个1,或两个1、一个,或一个1、两个,或三个,因而数列的个数为个数列
综上所述,数列的个数为 个
十大模板方法解决所有排列组合问题
(一)至少变恰好
某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36 B.72 C.108 D.144
【解析】根据题意,分3步进行分析:
①单位甲在6人中任选2人招聘,要求至少招聘一名男生,有种情况,
②单位乙在剩下的4人中任选2人招聘,有种情况,
③单位丙在剩下的2人中任选1人招聘,有种情况,
则有种不同的录取方案,选
2019年高考结束了,有为同学(其中巴蜀、一中各人,八中人)高考发挥不好,为了实现“南开梦”来到南开复读,现在学校决定把他们分到三个班,每个班至少分配位同学,为了让他们能更好的融入新的班级,规定来自同一学校的同学不能分到同一个班,则不同的分配方案种数为( )
A. B. C. D.
【解析】设这五人分别为,若A单独为一组时,只要2种分组方法;若A组含有两人时,有种分组方法;若A组含有三人时,有种分组情况;于是共有14种分组方法,所以分配方案总数共有,故选A.
(二)插空法
电视台在电视剧开播前连续播放6个不同的广告,其中4个商业广告2个公益广告,现要求2个公益广告不能连续播放,则不同的播放方式共有( )
A. B. C. D.
【解析】先排4个商业广告,有种排法,然后利用插空法,4个商业广告之间有5个空,插2个公益广告,有种排法,根据分步计数原理,所以共有种排法,选A.
某小区有排成一排的个车位,现有辆不同型号的车需要停放,如果要求剩下的个车位连在一起,那么不同的停放方法的种数为( )
A. B. C. D.
【解析】首先安排三辆车的位置,假设车位是从左到右一共7个,
当三辆车都在最左边时,有车之间的一个排列,
当左边两辆,最右边一辆时,有车之间的一个排列 ,
当左边一辆,最右边两辆时,有车之间的一个排列,
当最右边三辆时,有车之间的一个排列,
总上可知,共有不同的排列法种结果,所以选B
(三)特殊元素优先
某所大学在10月份举行秋季越野接力赛,每个专业四人一组,其中计算机专业的甲、乙、丙、丁四位大学生将代表本专业参加拉力赛,需要安排第一棒到第四棒的顺序,四个人去询问教练的安排,教练对甲说:“根据训练成绩,你和乙都不适合跑最后一棒”;然后又对乙说:“你还不适合安排在第一棒”,仅从教练回答的信息分析,要对这四名同学讲行合理的比赛棒次安排,那么不同情形的种数共有( )
A.6 B.8 C.12 D.24
【解析】根据条件乙只能安排在第二棒或第三棒;若“乙”安排在第二棒,此时有:种,若“乙”安排在第三棒,此时有:种,则一共有8种,选B.
(四)捆绑法
为迎接双流中学建校周年校庆,双流区政府计划提升双流中学办学条件.区政府联合双流中学组成工作组,与某建设公司计划进行个重点项目的洽谈,考虑到工程时间紧迫的现状,工作组对项目洽谈的顺序提出了如下要求:重点项目甲必须排在前三位,且项目丙、丁必须排在一起,则这六个项目的不同安排方案共有()
A.种 B.种 C.种 D.种
【解析】第一类:当甲在第位时,第一步,丙、丁捆绑成的整体有种方法,
第二步,丙、丁内部排列用种方法,
第三步,其他三人共种方法,共种方法;
第二类:当甲在第位时,第一步,丙、丁捆绑成的整体有种方法,
后面两步与第一类方法相同,共种方法;
第三类:当甲在第为时,与第二类相同,共种方法;
总计,完成这件事的方法数为,故选D.
某校迎新晚会上有个节目,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在前三位,且节目丙、丁必须排在一起.则该校迎新晚会节目演出顺序的编排方案共有( )
A.种 B.种 C.种 D.种
【解析】先考虑将丙、丁排在一起的排法种数,
将丙、丁捆绑在一起,与其他四人形成五个元素,排法种数为,
利用对称性思想,节目甲放在前三位或后三位的排法种数是一样的,
因此,该校迎新晚会节目演出顺序的编排方案共有种,选A.
(五)不在问题的间接法
某教师准备对一天的五节课进行课程安排,要求语文、数学、外语、物理、化学每科分别要排一节课,则数学不排第一节,物理不排最后一节的情况下,化学排第四节的概率是( )
A. B. C. D.
【解析】设事件:数学不排第一节,物理不排最后一节. 设事件:化学排第四节. ,,故满足条件的概率是.故选C.
某公司安排五名大学生从事四项工作,每项工作至少安排一人且每人只能安排一项工作,项工作仅安排一人,甲同学不能从事项工作,则不同的分配方案的种数为( )
A. B. C. D.
【解析】若甲同学在项工作,则剩余4人安排在B、C、D三项工作中,共有种
若甲同学不在项工作,,则在C或D工作,共有种,共36+96=132种,选C
某次文艺汇演为,要将A,B,C,D,E,F这六个不同节目编排成节目单,如下表:
序号 1 2 3 4 5 6
节目
如果A,B两个节目要相邻,且都不排在第3号位置,那么节目单上不同的排序方式有
A.192种 B.144种 C.96种 D.72种
【解析】由题意知A,B两个节目要相邻,且都不排在第3号位置,
可以把这两个元素看做一个,再让他们两个元素之间还有一个排列,
A,B两个节目可以排在1,2两个位置,可以排在4,5两个位置,可以排在5,6两个位置,
这两个元素共有种排法,其他四个元素要在剩下的四个位置全排列,
节目单上不同的排序方式有,选B.
(六)走街道问题
如图,某城市中,、两地有整齐的道路网,若规定只能向东或向北两个方向沿途中路线前进,则从到不同的走法共有( )
A.10 B.13 C.15 D.25
【解析】因为只能向东或向北两个方向,向北走的路有5条,向东走的路有3条,走路时向北走的路有5种结果,向东走的路有3种结果,根据分步计数原理知共有种结果,选C
(七)隔板法
设有个不同颜色的球,放入个不同的盒子中,要求每个盒子中至少有一个球,则不同的放法有( )
A.种 B.种 C.种 D.种
【解析】将两个颜色的球捆绑在一起,再全排列得 选D
将4个大小相同,颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里球的个数不小于该盒子的编号,则不同的放球方法有( )种.
A.7 B.10 C.14 D.20
【解析】根据题意,每个盒子里的球的个数不小于该盒子的编号,
分析可得,1号盒子至少放一个,最多放2个小球,分情况讨论:
①1号盒子中放1个球,其余3个放入2号盒子,有C41=4种方法;
②1号盒子中放2个球,其余2个放入2号盒子,有C42=6种方法;
则不同的放球方法有4+6=10种,选B.
(八)回归原始的方法
某次演出共有6位演员参加,规定甲只能排在第一个或最后一个出场, 乙和丙必须排在相邻的顺序出场,请问不同的演出顺序共有( )
A.24种 B.144种 C.48种 D.96种
【解析】第一步,先安排甲有种方案;第二步,安排乙和丙有种方案;第三步,安排剩余的三个演员有种方案,根据分步计数原理可得共有种方案.故选D.
如图,下有七张卡片,现这样组成一个三位数:甲从这七张卡片中随机抽出一张,把卡片上的数字写在百位,然后把卡片放回;乙再从这七张卡片中随机抽出一张,把卡片上的数字写在十位,然后把卡片放回;丙又从这七张卡片中随机抽出一张,把卡片上的数字写在个位,然后把卡片放回。则这样组成的三位数的个数为( )
A. B. C. D.
【解析】第一步:甲从七张卡片中随机抽出一张,抽到的不同取值为1,2,3,4,共4种情况;
第二步:乙从七张卡片中随机抽出一张,抽到的不同取值为1,2,3,4,共4种情况;
第三步:丙从七张卡片中随机抽出一张,抽到的不同取值为1,2,3,4,共4种情况;
因此,这样组成的三位数的个数为,故选C
(九)涂色
现有5种不同的颜色,给四棱锥P-ABCD的五个顶点涂色,要求同一条棱上的两个顶点颜色不能相同,一共有( )种方法.
A.240 B.360 C.420 D.480
【解析】当顶点A,C同色时,顶点P有5种颜色可供选择,点A有4种颜色可供选择,点B有3种颜色可供选择,此时C只能与A同色,1种颜色可选,点D就有3种颜色可选,共有种;
当顶点A,C不同色时,顶点P有5种颜色可供选择,点A有4种颜色可供选择,点B有3种颜色可供选择,此时C与A不同色,2种颜色可选,点D就有2种颜色可选,共有种;综上可得共有种,故选C.
一个正方形花圃,被分为5份A、B、C、D、E,种植红、黄、蓝、绿4种颜色不同的花,要求相邻两部分种植不同颜色的花,则不同的种植方法有( ).
A.24 种 B.48 种 C.84 种 D.96种
【解析】区域A、C、D两两相邻,共有种不同的种植方法,
当区域E与区域A种植相同颜色的花时,种植B、E有种不同的种植方法,
当区域E与区域A种植不同颜色的花时,种植B、E有种不同的种植方法,
∴不同的种植方法有种,选D
如图为我国数学家赵爽约3世纪初在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则区域涂色不相同的概率为
【解析】提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,
根据题意,如图,设5个区域依次为,分4步进行分析:
,对于区域,有5种颜色可选;
,对于区域与区域相邻,有4种颜色可选;
,对于区域,与区域相邻,有3种颜色可选;
,对于区域,若与颜色相同,区域有3种颜色可选,
若与颜色不相同,区域有2种颜色可选,区域有2种颜色可选,则区域有种选择,
则不同的涂色方案有种,
其中,区域涂色不相同的情况有:
,对于区域,有5种颜色可选;
,对于区域与区域相邻,有4种颜色可选;
,对于区域与区域相邻,有2种颜色可选;
,对于区域,若与颜色相同,区域有2种颜色可选,
若与颜色不相同,区域有2种颜色可选,区域有1种颜色可选,
则区域有种选择,不同的涂色方案有种,
区域涂色不相同的概率为 ,故选D.
(十)平均分堆与不平均分堆
《数术记遗》是《算经十书》中的一部,相传是汉末徐岳(约公元世纪)所著,该书主要记述了:积算(即筹算)太乙、两仪、三才、五行、八卦、九宫、运筹、了知、成数、把头、龟算、珠算计数种计算器械的使用方法某研究性学习小组人分工搜集整理种计算器械的相关资料,其中一人种、另两人每人种计算器械,则不同的分配方法有( )
A. B. C. D.
【解析】先将种计算器械分为三组,方法数有种,再排给个人,方法数有种,故选A.
为了落实中央提出的精准扶贫政策,永济市人力资源和社会保障局派人到开张镇石桥村包扶户贫困户,要求每户都有且只有人包扶,每人至少包扶户,则不同的包扶方案种数为( )
A. B. C. D.
【解析】由题意可知,这人所包扶的户数分别为、、或、、,
利用分步计数原理知,不同的包扶方案种数为,选C.
某班有50人,从中选10人均分2组(即每组5人),一组打扫教室,一组打扫操场,那么不同的选派法有( )
A. B. C. D.
【解析】先分组得,再一组打扫教室,一组打扫操场,得不同选法,选A
(一)至少问题
某班有20名女生和19名男生,从中选出5人组成一个垃圾分类宣传小组,要求女生和男生均不少于2人的选法共有( )
A. B.
C. D.
【解析】从中选出5人组成一个垃圾分类宣传小组,要求女生和男生均不少于2人
当选出5人为2女3男时,共有不同选法为种,当选出5人为3女2男时,共有不同选法为种
即选出5人组成一个垃圾分类宣传小组,要求女生和男生均不少于2人选法有种,选D
假设200件产品中有3件次品,现在从中任取5件,其中至少有2件次品的抽法有( )
A.种 B.种
C.种 D.种
【解析】根据题意,“至少有2件次品”可分为“有2件次品”与“有3件次品”两种情况
“有2件次品”的抽取方法有C32C1973种,“有3件次品”的抽取方法有C33C1972种
则共有C32C1973+C33C1972种不同的抽取方法,故选B
(二)不相邻问题插空法
有红色、黄色小球各两个,蓝色小球一个,所有小球彼此不同,现将五球排成一行,颜色相同者不相邻,不同的排法共有( )种
A.48 B.72 C.78 D.84
【解析】五个小球全排列共有:种排法
当两个红色小球与两个黄色小球都相邻时,共有:种排法
当两个红色小球相邻,两个黄色小球不相邻时,共有:种排法
当两个红色小球不相邻,两个黄色小球相邻时,共有:种排法
颜色相同的小球不相邻的排法共有:种排法,选
7人并排站成一行,如果甲、乙两人不相邻,那么不同的排法总数是
A.1440 B.3600 C.4320 D.4800
【解析】除甲、乙以外的5人全排列,共有种结果,5人排队后会出现6个空,从中选出2个排甲、乙,有种结果。所以满足条件的排队总数=(种),故选B
(三)相邻问题大元素法
2位男生和3位女生共5位同学站成一排,若3位女生中有且只有两位女生相邻,则不同排法的种数是
A.36 B.24 C.72 D.144
【解析】根据题意,把3位女生的两位捆绑在一起看做一个复合元素,和剩下的一位女生,
插入到2位男生全排列后形成的3个空中的2个空中,故有种,选.
2019年7月1日迎来了我国建党98周年,6名老党员在这天相约来到革命圣地之一的西柏坡.6名老党员中有3名党员当年在同一个班,他们站成一排拍照留念时,要求同班的3名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片0.5元(不含过塑费),且有一半的照片需要过塑,每张过塑费为0.75元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为( )
A.20.5 B.21元 C.21.5元 D.22元
【解析】捆绑法求得照片总数为,每名老党员需要支付照片费为元
(四)分配问题
高三年级有8个班级,分派4位数学老师任教,每个教师教两个班,则不同的分派方法有( )
A. B. C. D.
【解析】分两步,第一步将高三8个班级,两两一组分4组,共有种分法,第二步将4位数学老师分配到这4组,共有种情况,所以不同的分派方法有=,选B
将3名教师,5名学生分成3个小组,分别安排到甲、乙、丙三地参加社会实践活动,每地至少去1名教师和1名学生,则不同的安排方法总数为( )
A.1800 B.1440 C.300 D.900
【解析】先将3名教师安排到甲、乙、丙三地有种分法
然后安排5名学生,将5名学生可分为1,1,3三组,也可分为2,2,1三组
则安排到三地有种方法
根据分步乘法原理,可知不同的安排方法总数为种,故选D.
(五)特殊元素优先
10名运动员中有2名老队员和8名新队员,现从中选3人参加团体比赛,要求老队员至多1人入选且新队员甲不能入选的选法有( )
A.77种 B.144种 C.35种 D.72种
【解析】按照老队员的人数分两类:
(1)只选一名老队员,则新队员选2名(不含甲)有42
(2)没有选老队员,则选3名新队员(不含甲)有
所以老队员至多1人入选且新队员甲不能入选的选法有:种,故选A
中国古代儒家要求学生掌握六种基本才能(六艺):礼、乐、射、御、书、数。某校国学社团周末开展“六艺”课程讲座活动,一天连排六节,每艺一节,排课有如下要求:“射”不能排在第一,“数”不能排在最后,则“六艺”讲座不同的排课顺序共有______种.
【解析】第一种情况,当“射”排最后一位时,共有种方法
第二种情况,当“射”排中间4个位置中的1个时共有种方法
不同的排列方式共有种
所以“六艺”讲座不同的排课顺序共有504种
2位男生和3位女生共5位同学站成一排,若3位女生中有且只有两位女生相邻,则不同排法的种数是
A.36 B.24 C.72 D.144
【解析】根据题意,把3位女生的两位捆绑在一起看做一个复合元素,和剩下的一位女生,
插入到2位男生全排列后形成的3个空中的2个空中,故有种,选
(六)涂色问题
如图,用5种不同的颜色把图中、、、四块区域分开,若相邻区域不能涂同一种颜色,则不同的涂法共有( )
A.200种 B.160种 C.240种 D.180种
【解析】涂有5种涂法,有4种,有3种,因为可与同色,故有3种,
∴由分步乘法计数原理知,不同涂法有种.故答案选D。
如图,有一种游戏画板,要求参与者用六种颜色给画板涂色,这六种颜色分别为红色、黄色1、黄色2、黄色3、金色1、金色2,其中黄色1、黄色2、黄色3是三种不同的颜色,金色1、金色2是两种不同的颜色,要求红色不在两端,黄色1、黄色2、黄色3有且仅有两种相邻,则不同的涂色方案有( )
A.120种 B.240种 C.144种 D.288种
【解析】不考虑红色的位置,黄色1、黄色2、黄色3有且仅有两个相邻的涂色方案有种. 这种情况下,红色在左右两端的涂色方案有种;从而所求的结果为种,故选D.
如图所示的几何体是由一个正三棱锥P-ABC与正三棱柱ABC-A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有( )
A.24种 B.18种 C.16种 D.12种
【解析】先对正三棱锥P-ABC三个表面染色,有种
再对正三棱柱ABC-A1B1C1三个表面染色有种
所以共有种,选D.
(七)数字整除问题
由数字0,1,2,3组成的无重复数字且能被3整除的非一位数的个数为( )
A.12 B.20 C.30 D.31
【解析】两位数:含数字1,2的数有个,或含数字3,0的数有1个. 三位数:含数字0,1,2的数有个,含数字1,2,3有个. 四位数:有个. 所以共有个,
故选D.
如果把个位数是,且恰有个数字相同的四位数叫做“伪豹子数”那么在由,,,,五个数字组成的有重复数字的四位数中,“伪豹子数”共有( )个
A. B. C. D.
【解析】相同数不为1时,四位数的个位数是1,其他3个相同的数可能是2,3,4,5共4种
相同数为1时,四位数的个位数是1,在2,3,4,5中选一个数放在十位或百位或千位上,共有种
则共有种,故选A
(八)正难则反
某电商为某次活动设计了“和谐”、“爱国”、“敬业”三种红包,活动规定每人可以依次点击4次,每次都会获得三种红包的一种,若集全三种即可获奖,但三种红包出现的顺序不同对应的奖次也不同员工甲按规定依次点击了4次,直到第4次才获奖则他获得奖次的不同情形种数为
A.9 B.12 C.18 D.24
【解析】根据题意,若员工甲直到第4次才获奖,则其第4次才集全“和谐”、“爱国”、“敬业”三种红包
则甲第4次获得的红包有3种情况
前三次获得的红包为其余的2种,有种情况
则他获得奖次的不同情形种数为种,选C
把20个相同的小球装入编号分别为①②③④的4个盒子里,要求①②号盒每盒至少3个球,③④号盒每盒至少4个球,共有( )种方法.
A. B. C. D.
【解析】设四个盒子中装的小球个数分别为,,,,则
要求①②号盒每盒至少3个球,③④号盒每盒至少4个球
令,,,,则,,,都大于或等于1,且
问题相当于将10个球分成四部分,在10个球的9个间隔里选三个隔开,有种方法,选A
(九)避免出错---彻底分类
今有个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有( )种
A. B. C. D.
【解析】第一类:只用两辆缆车,
若两个小孩坐在一块,则有种乘车方式;
若两个小孩不坐在一块,则有种乘车方式
第二类:用三辆缆车
若两个小孩坐在一块,则有种乘车方式
若两个小孩不坐在一块,则有种乘车方式
综上不同的乘车方式有种,故选C
某学校要安排2名高二的同学,2名高一的同学和名初三的同学去参加电视节目《变形记》,有五个乡村小镇A、B、C、D,E(每名同学选择一个小镇)由于某种原因高二的同学不去小镇A,高一的同学不去小镇B,初三的同学不去小镇D和E,则共有________种不同的安排方法(用数字作)
【解析】如果初三学生去,则高二学生选人去,另外三人去,故方法数有种
如果初三学生去,则高一学生选人去,另外三人去,故方法数有种
如果初三学生去,则高二学生选人去,高一学生选人去,另外两人去,有种
故总的方法数有种
(十)空间几何体与排列组合
已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为
A.40 B.16 C.13 D.10
【解析】分两类情况讨论:第1类,直线a分别与直线b上的8个点可以确定8个不同的平面;第2类,直线b分别与直线a上的5个点可以确定5个不同的平面.
根据分类加法计数原理知,共可以确定8+5=13个不同的平面,故选C.
在一个质地均匀的四面体中,一个面上标有数字1,一个面上标有数字2,另外有两个面上标有数字3,将该正四面体抛掷三次,则向下一面的数字之和为7的情况有________种
【解析】因为四面体中,一个面上标有数字1,一个面上标有数字2,另外有两个面上标有数字3,当将该正四面体抛掷三次,则向下一面的数字之和为7的情况有两类:
当组合为2,2,3时,可能有种情况
当组合为1,3,3时,可能有种情况
综上可知,所有出现向下一面的数字之和为7的情况有种
(十一)排列组合综合问题
空间中不共面的4点A,B,C,D,若其中3点到平面的距离相等且为第四个点到平面的2倍,这样的平面的个数为( )
A.8 B.16 C.32 D.48
【解析】第一种情况,A,B,C,D点在平面的同侧.
当平面∥平面BCD时,A与平面的距离是与平面BCD的距离的2倍.
这种情况下有4个平面.
第二种情况,A,B,C,D中有3个点在平面的一侧,第4个点在平面的另一侧,这时又有两种情形:
一种情形是平面与平面BCD平行,且A与平面距离是平面与平面BCD距离的2倍.这时有4个平面.
另一种情形如图a所示,图中E,F分别是AB,AC的中点,K是AD的三等分点中靠近A的分点,A,B,C到平面EFK(即平面)的距离是D到平面EFK距离的一半.
∵EF可以是AB,AC的中点的连线,又可以是AB,BC的中点的连线,或AC,BC的中点的连线,
∴这种情形下的平面有3×4=12(个).
第三种情况,如图b所示,在A,B,C,D四点中,平面两侧各种有两点.
容易看出:点A到平面EFMN(平面)的距离是B,C,D到该平面距离的2倍。
就A,C与B,D分别位于平面两侧的情形来看,就有A离平面远,B离平面远,C离平面远,D离平面远这四种情况.
又“AC,BD异面,则这样的异面直线共有3对
∴平面有4×3=12(个).
综上分析,平面有4+4+12+12=32(个),选C
若矩阵满足下列条件:①每行中的四个数均为集合{1,2,3,4}中不同元素;②四列中有且只有两列的上下两数是相同的,则满足①②条件的矩阵的个数为( )
A.48 B.72 C.144 D.264
【解析】第一步,排列第一行,有种排列方法;
第二步,由题意知有且只有两列的上下两数是相同的,选择中的两个数作为与上列相同的数字,有种取法,而对于剩余两数,为使不与上列数字相同,有且只有一种排法,
因此,满足题中条件的矩阵的个数共有个,故选C.
如图,平面中有梯形与梯形分别在直线的两侧,它们与无公共点,并且关于成轴对称,现将沿折成一个直二面角,则,,,,,,,八个点可以确定平面的个数是( )
A.56 B.44 C.32 D.16
【解析】由题设从八个顶点中任取三个确定的所有平面的个数个,其中六个平面中任取三个点所确定的平面个数为个,故,,,,,,,八个点可以确定平面的个数是,选C
中国古代儒家要求学生掌握六种基本才能:礼、乐、射、御、书、数.“礼”,礼节,即今德育:“乐”,音乐,“射”和“御”,射箭和驾驭马车的技术,即今体育和劳动:“书”,书法,即今文学;“数”,算法,即今数学。某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”必须排在第一,“数”不能排在最后,“射”和“御”要相邻,则“六艺”讲座不同的排课顺序共有( )
A.种 B.种 C.种 D.种
【解析】如果“射”或“御”排在最后,那么“射”和“御”有两种排法即种,余下3种才能共有种排法,故此时共有中排法;
如果“射”和“御”均不在最后,那么“射”和“御”有种排法,中间还余两个位置,两个位置可选一个给“数”,有2种排法,余下两个位置放置最后的两个基本才能,有,故共有种排法,
综上,共有36种排法,选B.
已知数列,.满足条件“”的数列个数为_____.
【解析】因为,所以只能取0或1
而
所以中出现0的个数可以是6个,5个,4个,3个。
若出现6个0,则数列为常数数列,共有1个数列。
若出现5个0,则出现一个1,或一个,因而数列个数为个数列。
若出现4个0,出现两个1,或两个,或一个1、一个,数列个数为个数列
若出现3个0,则出现三个1,或两个1、一个,或一个1、两个,或三个,因而数列的个数为个数列
综上所述,数列的个数为 个
十大模板方法解决所有排列组合问题
(一)至少变恰好
某地区甲、乙、丙三所单位进行招聘,其中甲单位招聘2名,乙单位招聘2名,丙单位招聘1名,并且甲单位要至少招聘一名男生,现有3男3女参加三所单位的招聘,则不同的录取方案种数为( )
A.36 B.72 C.108 D.144
【解析】根据题意,分3步进行分析:
①单位甲在6人中任选2人招聘,要求至少招聘一名男生,有种情况,
②单位乙在剩下的4人中任选2人招聘,有种情况,
③单位丙在剩下的2人中任选1人招聘,有种情况,
则有种不同的录取方案,选
2019年高考结束了,有为同学(其中巴蜀、一中各人,八中人)高考发挥不好,为了实现“南开梦”来到南开复读,现在学校决定把他们分到三个班,每个班至少分配位同学,为了让他们能更好的融入新的班级,规定来自同一学校的同学不能分到同一个班,则不同的分配方案种数为( )
A. B. C. D.
【解析】设这五人分别为,若A单独为一组时,只要2种分组方法;若A组含有两人时,有种分组方法;若A组含有三人时,有种分组情况;于是共有14种分组方法,所以分配方案总数共有,故选A.
(二)插空法
电视台在电视剧开播前连续播放6个不同的广告,其中4个商业广告2个公益广告,现要求2个公益广告不能连续播放,则不同的播放方式共有( )
A. B. C. D.
【解析】先排4个商业广告,有种排法,然后利用插空法,4个商业广告之间有5个空,插2个公益广告,有种排法,根据分步计数原理,所以共有种排法,选A.
某小区有排成一排的个车位,现有辆不同型号的车需要停放,如果要求剩下的个车位连在一起,那么不同的停放方法的种数为( )
A. B. C. D.
【解析】首先安排三辆车的位置,假设车位是从左到右一共7个,
当三辆车都在最左边时,有车之间的一个排列,
当左边两辆,最右边一辆时,有车之间的一个排列 ,
当左边一辆,最右边两辆时,有车之间的一个排列,
当最右边三辆时,有车之间的一个排列,
总上可知,共有不同的排列法种结果,所以选B
(三)特殊元素优先
某所大学在10月份举行秋季越野接力赛,每个专业四人一组,其中计算机专业的甲、乙、丙、丁四位大学生将代表本专业参加拉力赛,需要安排第一棒到第四棒的顺序,四个人去询问教练的安排,教练对甲说:“根据训练成绩,你和乙都不适合跑最后一棒”;然后又对乙说:“你还不适合安排在第一棒”,仅从教练回答的信息分析,要对这四名同学讲行合理的比赛棒次安排,那么不同情形的种数共有( )
A.6 B.8 C.12 D.24
【解析】根据条件乙只能安排在第二棒或第三棒;若“乙”安排在第二棒,此时有:种,若“乙”安排在第三棒,此时有:种,则一共有8种,选B.
(四)捆绑法
为迎接双流中学建校周年校庆,双流区政府计划提升双流中学办学条件.区政府联合双流中学组成工作组,与某建设公司计划进行个重点项目的洽谈,考虑到工程时间紧迫的现状,工作组对项目洽谈的顺序提出了如下要求:重点项目甲必须排在前三位,且项目丙、丁必须排在一起,则这六个项目的不同安排方案共有()
A.种 B.种 C.种 D.种
【解析】第一类:当甲在第位时,第一步,丙、丁捆绑成的整体有种方法,
第二步,丙、丁内部排列用种方法,
第三步,其他三人共种方法,共种方法;
第二类:当甲在第位时,第一步,丙、丁捆绑成的整体有种方法,
后面两步与第一类方法相同,共种方法;
第三类:当甲在第为时,与第二类相同,共种方法;
总计,完成这件事的方法数为,故选D.
某校迎新晚会上有个节目,考虑整体效果,对节目演出顺序有如下要求:节目甲必须排在前三位,且节目丙、丁必须排在一起.则该校迎新晚会节目演出顺序的编排方案共有( )
A.种 B.种 C.种 D.种
【解析】先考虑将丙、丁排在一起的排法种数,
将丙、丁捆绑在一起,与其他四人形成五个元素,排法种数为,
利用对称性思想,节目甲放在前三位或后三位的排法种数是一样的,
因此,该校迎新晚会节目演出顺序的编排方案共有种,选A.
(五)不在问题的间接法
某教师准备对一天的五节课进行课程安排,要求语文、数学、外语、物理、化学每科分别要排一节课,则数学不排第一节,物理不排最后一节的情况下,化学排第四节的概率是( )
A. B. C. D.
【解析】设事件:数学不排第一节,物理不排最后一节. 设事件:化学排第四节. ,,故满足条件的概率是.故选C.
某公司安排五名大学生从事四项工作,每项工作至少安排一人且每人只能安排一项工作,项工作仅安排一人,甲同学不能从事项工作,则不同的分配方案的种数为( )
A. B. C. D.
【解析】若甲同学在项工作,则剩余4人安排在B、C、D三项工作中,共有种
若甲同学不在项工作,,则在C或D工作,共有种,共36+96=132种,选C
某次文艺汇演为,要将A,B,C,D,E,F这六个不同节目编排成节目单,如下表:
序号 1 2 3 4 5 6
节目
如果A,B两个节目要相邻,且都不排在第3号位置,那么节目单上不同的排序方式有
A.192种 B.144种 C.96种 D.72种
【解析】由题意知A,B两个节目要相邻,且都不排在第3号位置,
可以把这两个元素看做一个,再让他们两个元素之间还有一个排列,
A,B两个节目可以排在1,2两个位置,可以排在4,5两个位置,可以排在5,6两个位置,
这两个元素共有种排法,其他四个元素要在剩下的四个位置全排列,
节目单上不同的排序方式有,选B.
(六)走街道问题
如图,某城市中,、两地有整齐的道路网,若规定只能向东或向北两个方向沿途中路线前进,则从到不同的走法共有( )
A.10 B.13 C.15 D.25
【解析】因为只能向东或向北两个方向,向北走的路有5条,向东走的路有3条,走路时向北走的路有5种结果,向东走的路有3种结果,根据分步计数原理知共有种结果,选C
(七)隔板法
设有个不同颜色的球,放入个不同的盒子中,要求每个盒子中至少有一个球,则不同的放法有( )
A.种 B.种 C.种 D.种
【解析】将两个颜色的球捆绑在一起,再全排列得 选D
将4个大小相同,颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里球的个数不小于该盒子的编号,则不同的放球方法有( )种.
A.7 B.10 C.14 D.20
【解析】根据题意,每个盒子里的球的个数不小于该盒子的编号,
分析可得,1号盒子至少放一个,最多放2个小球,分情况讨论:
①1号盒子中放1个球,其余3个放入2号盒子,有C41=4种方法;
②1号盒子中放2个球,其余2个放入2号盒子,有C42=6种方法;
则不同的放球方法有4+6=10种,选B.
(八)回归原始的方法
某次演出共有6位演员参加,规定甲只能排在第一个或最后一个出场, 乙和丙必须排在相邻的顺序出场,请问不同的演出顺序共有( )
A.24种 B.144种 C.48种 D.96种
【解析】第一步,先安排甲有种方案;第二步,安排乙和丙有种方案;第三步,安排剩余的三个演员有种方案,根据分步计数原理可得共有种方案.故选D.
如图,下有七张卡片,现这样组成一个三位数:甲从这七张卡片中随机抽出一张,把卡片上的数字写在百位,然后把卡片放回;乙再从这七张卡片中随机抽出一张,把卡片上的数字写在十位,然后把卡片放回;丙又从这七张卡片中随机抽出一张,把卡片上的数字写在个位,然后把卡片放回。则这样组成的三位数的个数为( )
A. B. C. D.
【解析】第一步:甲从七张卡片中随机抽出一张,抽到的不同取值为1,2,3,4,共4种情况;
第二步:乙从七张卡片中随机抽出一张,抽到的不同取值为1,2,3,4,共4种情况;
第三步:丙从七张卡片中随机抽出一张,抽到的不同取值为1,2,3,4,共4种情况;
因此,这样组成的三位数的个数为,故选C
(九)涂色
现有5种不同的颜色,给四棱锥P-ABCD的五个顶点涂色,要求同一条棱上的两个顶点颜色不能相同,一共有( )种方法.
A.240 B.360 C.420 D.480
【解析】当顶点A,C同色时,顶点P有5种颜色可供选择,点A有4种颜色可供选择,点B有3种颜色可供选择,此时C只能与A同色,1种颜色可选,点D就有3种颜色可选,共有种;
当顶点A,C不同色时,顶点P有5种颜色可供选择,点A有4种颜色可供选择,点B有3种颜色可供选择,此时C与A不同色,2种颜色可选,点D就有2种颜色可选,共有种;综上可得共有种,故选C.
一个正方形花圃,被分为5份A、B、C、D、E,种植红、黄、蓝、绿4种颜色不同的花,要求相邻两部分种植不同颜色的花,则不同的种植方法有( ).
A.24 种 B.48 种 C.84 种 D.96种
【解析】区域A、C、D两两相邻,共有种不同的种植方法,
当区域E与区域A种植相同颜色的花时,种植B、E有种不同的种植方法,
当区域E与区域A种植不同颜色的花时,种植B、E有种不同的种植方法,
∴不同的种植方法有种,选D
如图为我国数学家赵爽约3世纪初在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则区域涂色不相同的概率为
【解析】提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,
根据题意,如图,设5个区域依次为,分4步进行分析:
,对于区域,有5种颜色可选;
,对于区域与区域相邻,有4种颜色可选;
,对于区域,与区域相邻,有3种颜色可选;
,对于区域,若与颜色相同,区域有3种颜色可选,
若与颜色不相同,区域有2种颜色可选,区域有2种颜色可选,则区域有种选择,
则不同的涂色方案有种,
其中,区域涂色不相同的情况有:
,对于区域,有5种颜色可选;
,对于区域与区域相邻,有4种颜色可选;
,对于区域与区域相邻,有2种颜色可选;
,对于区域,若与颜色相同,区域有2种颜色可选,
若与颜色不相同,区域有2种颜色可选,区域有1种颜色可选,
则区域有种选择,不同的涂色方案有种,
区域涂色不相同的概率为 ,故选D.
(十)平均分堆与不平均分堆
《数术记遗》是《算经十书》中的一部,相传是汉末徐岳(约公元世纪)所著,该书主要记述了:积算(即筹算)太乙、两仪、三才、五行、八卦、九宫、运筹、了知、成数、把头、龟算、珠算计数种计算器械的使用方法某研究性学习小组人分工搜集整理种计算器械的相关资料,其中一人种、另两人每人种计算器械,则不同的分配方法有( )
A. B. C. D.
【解析】先将种计算器械分为三组,方法数有种,再排给个人,方法数有种,故选A.
为了落实中央提出的精准扶贫政策,永济市人力资源和社会保障局派人到开张镇石桥村包扶户贫困户,要求每户都有且只有人包扶,每人至少包扶户,则不同的包扶方案种数为( )
A. B. C. D.
【解析】由题意可知,这人所包扶的户数分别为、、或、、,
利用分步计数原理知,不同的包扶方案种数为,选C.
某班有50人,从中选10人均分2组(即每组5人),一组打扫教室,一组打扫操场,那么不同的选派法有( )
A. B. C. D.
【解析】先分组得,再一组打扫教室,一组打扫操场,得不同选法,选A
同课章节目录
