§1-4 角平分线(1)性质定理与逆定理
文档属性
| 名称 | §1-4 角平分线(1)性质定理与逆定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 316.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-03 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
九年级数学(上册)第一章 证明(二)
角平分线
你还能利用折纸的方法得到角平分线及角平分线上的点吗
回顾 思考
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PB⊥OB,垂足分别是D,B.
求证:PD=PB.
而△OPD≌△OPB的条件由已知易知它满足公理(AAS).
故结论可证.
老师期望:你能写出规范的证明过程.
分析:要证明PD=PB,只要证明它们所在的△OPD≌△OPB,
你还记得角平分线上的点有什么性质吗
角平分线上的点到这个角的两边距离相等.
能证明这一结论吗
O
C
1
A
2
P
D
B
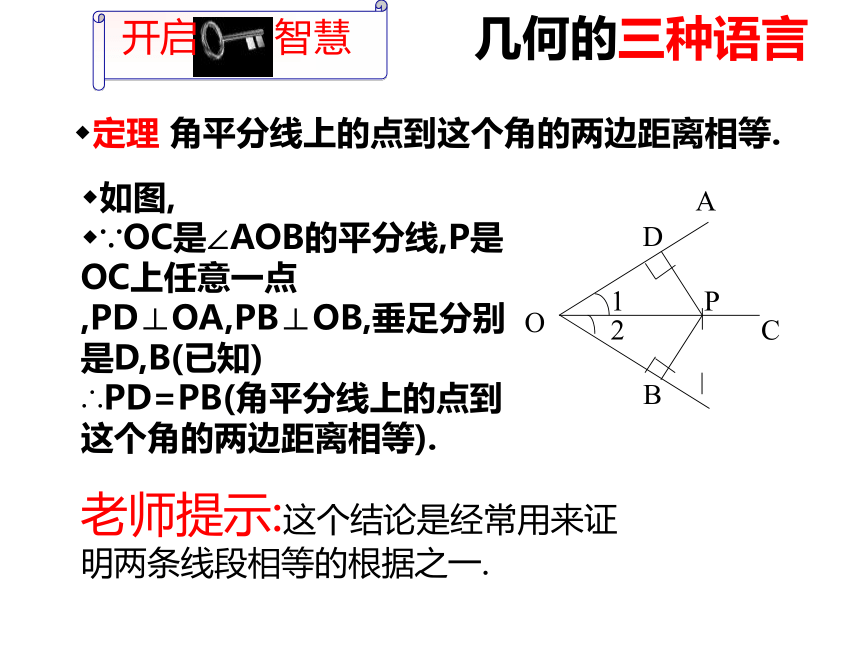
几何的三种语言
定理 角平分线上的点到这个角的两边距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.
开启 智慧
如图,
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PB⊥OB,垂足分别是D,B(已知)
∴PD=PB(角平分线上的点到这个角的两边距离相等).
O
C
1
A
2
P
D
B
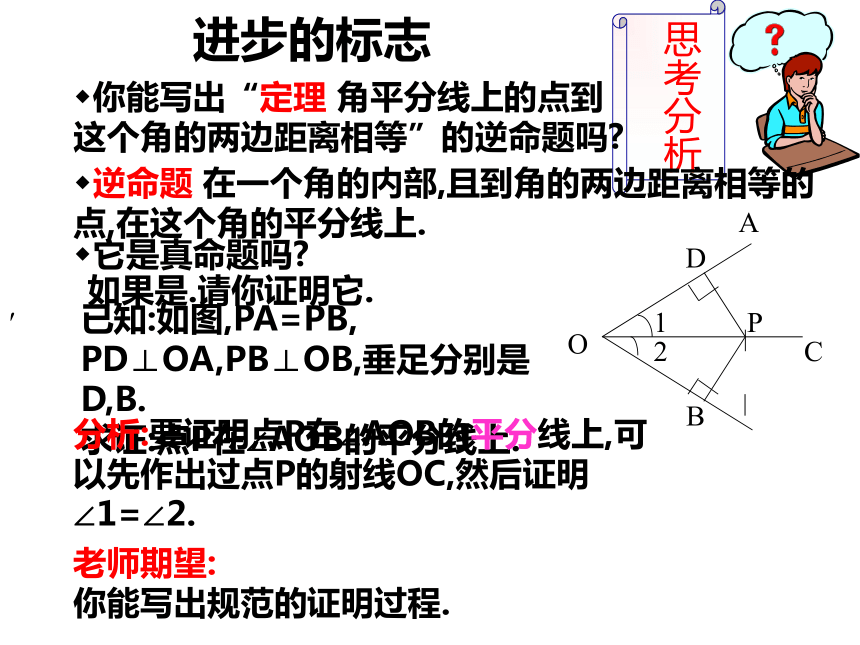
进步的标志
′
思考分析
你能写出“定理 角平分线上的点到这个角的两边距离相等”的逆命题吗
逆命题 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
它是真命题吗
如果是.请你证明它.
已知:如图,PA=PB, PD⊥OA,PB⊥OB,垂足分别是D,B.
求证:点P在∠AOB的平分线上.
分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠1=∠2.
老师期望:
你能写出规范的证明过程.
O
C
1
A
2
P
D
B
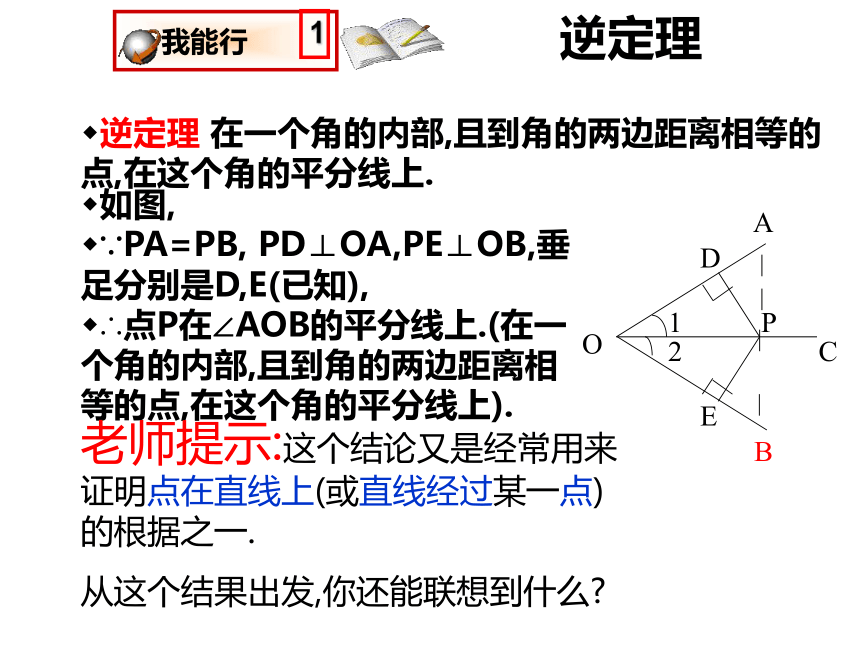
逆定理
我能行
1
逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
如图,
∵PA=PB, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
从这个结果出发,你还能联想到什么
O
C
B
1
A
2
P
D
E
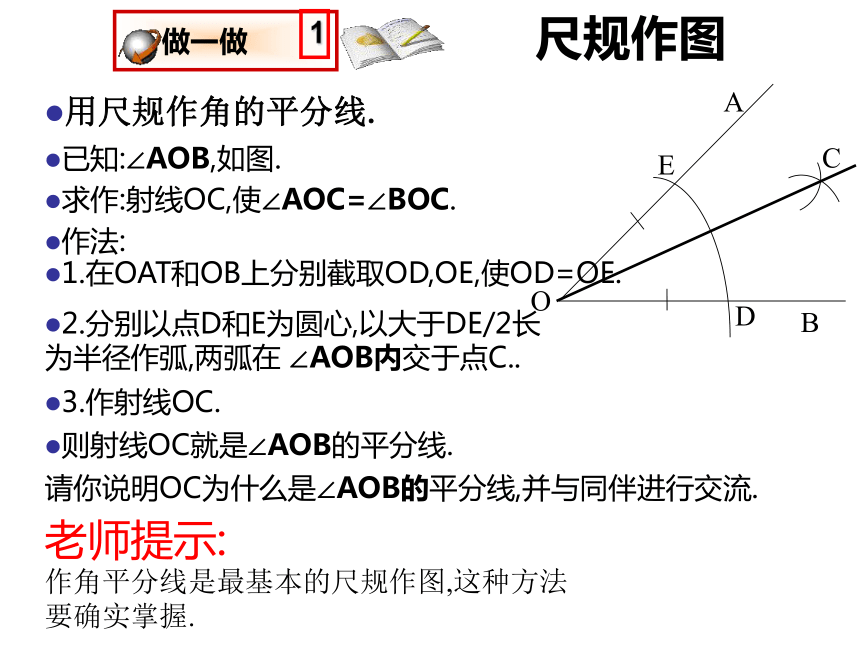
尺规作图
做一做
1
已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC.
作法:
用尺规作角的平分线.
1.在OAT和OB上分别截取OD,OE,使OD=OE.
2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在 ∠AOB内交于点C..
3.作射线OC.
请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.
老师提示:
作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
O
C
则射线OC就是∠AOB的平分线.
D
E
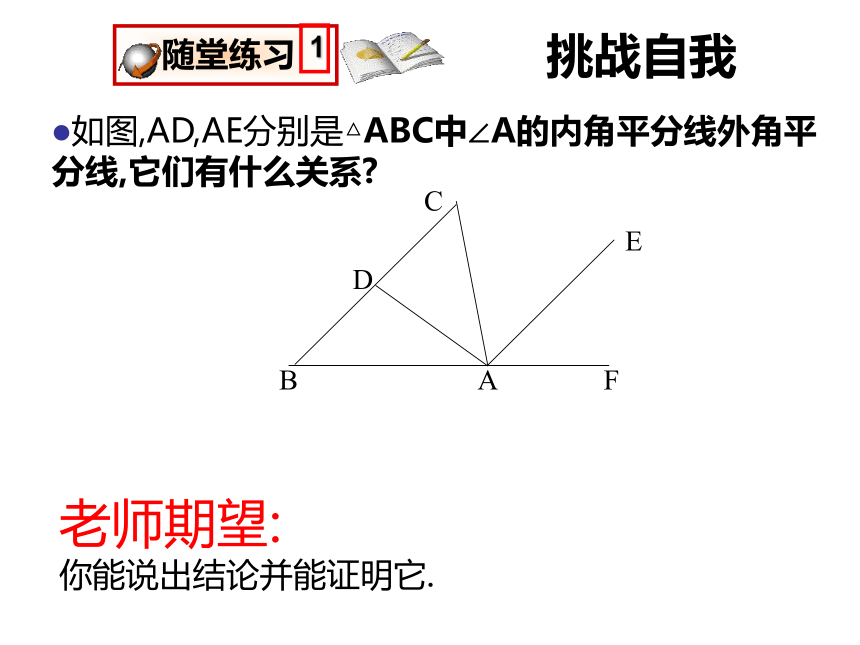
挑战自我
随堂练习
1
如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系
老师期望:
你能说出结论并能证明它.
E
D
A
B
C
F
梦想成真
随堂练习
2
2.如图,一目标在A区,到期公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺 1:20 000).
A区
习题1.8
独立作业
1
1.利用尺规作出三角形三个内角的平分线.
老师期望:
先分别作出不同形状的三角形,再按要求去作图.
你发现了什么?
习题1.8
独立作业
2
2. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
老师期望:
养成用数学解释生活的习惯.
C●
D●
A
B
O
3.我校初二年级的四个班级同学参加义务劳动,其中有两个班的同学分别在D、E两处参加劳动,另外两个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P ,使P到两条道路的距离相等,且使 PD= PE,请你找出点P的位置。
习题1.8
独立作业
3
4.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
B
A
E
D
C
F
回味无穷
定理 角平分线上的点到这个角的两边距离相等.
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
∵PA=PB, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
用尺规作角的平分线.
邻补角的角平分线之间的关系.
如
小结 拓展
O
C
B
1
A
2
P
D
E
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
下课了!
九年级数学(上册)第一章 证明(二)
角平分线
你还能利用折纸的方法得到角平分线及角平分线上的点吗
回顾 思考
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PB⊥OB,垂足分别是D,B.
求证:PD=PB.
而△OPD≌△OPB的条件由已知易知它满足公理(AAS).
故结论可证.
老师期望:你能写出规范的证明过程.
分析:要证明PD=PB,只要证明它们所在的△OPD≌△OPB,
你还记得角平分线上的点有什么性质吗
角平分线上的点到这个角的两边距离相等.
能证明这一结论吗
O
C
1
A
2
P
D
B
几何的三种语言
定理 角平分线上的点到这个角的两边距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.
开启 智慧
如图,
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PB⊥OB,垂足分别是D,B(已知)
∴PD=PB(角平分线上的点到这个角的两边距离相等).
O
C
1
A
2
P
D
B
进步的标志
′
思考分析
你能写出“定理 角平分线上的点到这个角的两边距离相等”的逆命题吗
逆命题 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
它是真命题吗
如果是.请你证明它.
已知:如图,PA=PB, PD⊥OA,PB⊥OB,垂足分别是D,B.
求证:点P在∠AOB的平分线上.
分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠1=∠2.
老师期望:
你能写出规范的证明过程.
O
C
1
A
2
P
D
B
逆定理
我能行
1
逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
如图,
∵PA=PB, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.
从这个结果出发,你还能联想到什么
O
C
B
1
A
2
P
D
E
尺规作图
做一做
1
已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC.
作法:
用尺规作角的平分线.
1.在OAT和OB上分别截取OD,OE,使OD=OE.
2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在 ∠AOB内交于点C..
3.作射线OC.
请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.
老师提示:
作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
O
C
则射线OC就是∠AOB的平分线.
D
E
挑战自我
随堂练习
1
如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系
老师期望:
你能说出结论并能证明它.
E
D
A
B
C
F
梦想成真
随堂练习
2
2.如图,一目标在A区,到期公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺 1:20 000).
A区
习题1.8
独立作业
1
1.利用尺规作出三角形三个内角的平分线.
老师期望:
先分别作出不同形状的三角形,再按要求去作图.
你发现了什么?
习题1.8
独立作业
2
2. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
老师期望:
养成用数学解释生活的习惯.
C●
D●
A
B
O
3.我校初二年级的四个班级同学参加义务劳动,其中有两个班的同学分别在D、E两处参加劳动,另外两个班的同学分别在道路AB、AC两处劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P ,使P到两条道路的距离相等,且使 PD= PE,请你找出点P的位置。
习题1.8
独立作业
3
4.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
B
A
E
D
C
F
回味无穷
定理 角平分线上的点到这个角的两边距离相等.
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
∵PA=PB, PD⊥OA,PE⊥OB,垂足分别是D,E(已知),
∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).
用尺规作角的平分线.
邻补角的角平分线之间的关系.
如
小结 拓展
O
C
B
1
A
2
P
D
E
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
下课了!
