2020-2021学年高二下学期数学苏教版选修2-2第一章1.1.1平均变化率学案
文档属性
| 名称 | 2020-2021学年高二下学期数学苏教版选修2-2第一章1.1.1平均变化率学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 216.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览


文档简介
1.1.1 平均变化率
学习目标:1.学会通过对一些实例的直观感知,构建平均变化率的概念,并初步运用和加
深理解利用平均变化率来刻画变量变化得快与慢的原理;
2.理解并会求具体函数的平均变化率.
学习重点:了解平均变化率概念的形成过程,会利用平均变化率来刻画变量变化得快与慢.
会在具体的环境中说明平均变化率的实际意义.
学习难点:对平均变化率概念的本质的理解;对生活现象作出数学解释.
【明标自学】预习课本P5-7理清下列概念,完成相应问题。
1.问题情境.
法国《队报》网站的文章称刘翔以不可思议的速度统治了赛场.这名21岁的中国人跑的几乎比炮弹还快.赛道上显示的12.94秒的成绩已经打破了12.95秒的奥运会纪录,但经过验证他是以12.91秒的成绩追平了世界纪录,他的平均速度达到了8.52m/s.
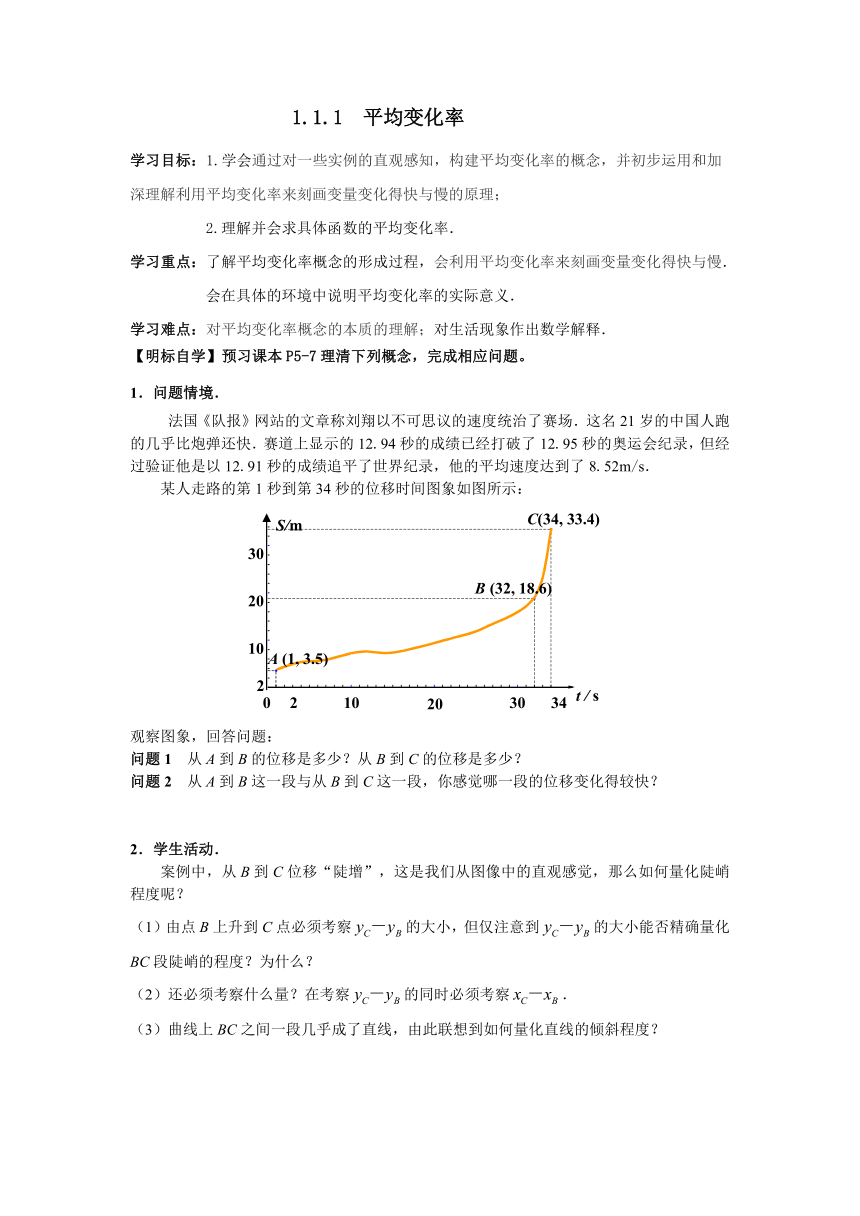
某人走路的第1秒到第34秒的位移时间图象如图所示:
观察图象,回答问题:
问题1 从A到B的位移是多少?从B到C的位移是多少?
问题2 从A到B这一段与从B到C这一段,你感觉哪一段的位移变化得较快?
2.学生活动.
案例中,从B到C位移“陡增”,这是我们从图像中的直观感觉,那么如何量化陡峭程度呢?
(1)由点B上升到C点必须考察的大小,但仅注意到的大小能否精确量化BC段陡峭的程度?为什么?
(2)还必须考察什么量?在考察的同时必须考察.
(3)曲线上BC之间一段几乎成了直线,由此联想到如何量化直线的倾斜程度?
【建构数学】
1.平均变化率:
(1)定义:一般地,函数在区间上的平均变化率为
注意:平均变化率不能脱离区间而言
(2)实质: 的改变量与 的改变量之比.
(3)意义:刻画函数值在区间[x1,x2]上变化的 .
2.平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“视觉化”.
思考:(1)若设,即将看作是对于的一个增量,
则在平均变化率为 .
(2)在平均变化率的几何意义即为 .
【自学检测】
1.在平均变化率的定义中,自变量的增量Δx满足( )
A.Δx<0 B.Δx>0 C.Δx=0 D.Δx≠0
2.设函数y=f(x),当自变量x由x0改变到x0+Δx时,函数值的改变量Δy=( )
A.f(x0+Δx) B.f(x0)+Δx C.f(x0)·Δx D.f(x0+Δx)-f(x0)
3.判断下列命题正确还是错误。
(1)若函数,则在上的平均变化率为.( )
(2)若函数在上的平均变化率小于其在上的平均变化率,所以在上不如在上变化的快.( )
(3)平均变化率不能反映函数值变化的快慢.( )
4.函数在上的平均变化率为________.
【典型例题】
例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到
第3个月以及第6个月到第12个月该婴儿体重的平均变化率.
例2 水经过虹吸管从容器甲流向容器乙,s后容器甲中的水的体积(单位:cm3),试计算第一个10s内的平均变化率.
例3.已知函数,分别计算在区间,上函数及的平均变化率.
思考:从本题的求解中,你能发现一次函数在区间上的平均变化率有什么特点吗?
例4 已知函数,分别计算在下列区间上的平均变化率:
[1,3] ⑤ [0.9,1]
[1,2] ⑥ [0.99,1]
[1,1.1] ⑦ [0.999,1]
[1,1.001] ⑧ [0.9999,1]
思考: 本题中八个区间的变化导致平均变化率有怎样的变化?这种变化的实际意义和数学意义分别是什么?
【当堂检测】
1.函数y=x2+ax+b,当自变量由0变化到1时,函数值的变化量为________.
2.在曲线y=x2+1的图象上取一点(1,2)及相邻的一点(1.1,2.21),则该曲线在[1,1.1]上的平均变化率为________.
3.已知函数f (x)=x2-2x
(1)求f (x)在2到2.1之间的平均变化率.;
(2)求f (x)在x=2到x=2+Δx之间的平均变化率;
(3)求f (x)在x0到x0+Δx之间的平均变化率。
4.为了检测甲、乙两辆车的刹车性能,分别对两辆车进行了测试,甲从25 m/s到0 m/s花了5 s,乙从18 m/s到0 m/s花了4 s,试比较两辆车的刹车性能.
【课堂小结】
【课后作业】
1.已知函数f(x)=2x2-4的图象上一点(1,-2)及邻近一点(1+Δx,-2+Δy),则等于( )
A.4 B.4x C.4+2Δx D.4+2(Δx)2
2.物体做直线运动所经过的路程s可以表示为时间t的函数s=s(t),则物体在时间间隔[t0,t0+Δt]内的平均速度是( )
A.v0 B. C. D.
3.如果质点M按规律s=3+t2运动,则在一小段时间[2,2.1]中相应的平均速度是________(m/s).
4.函数y=sin x在上的平均变化率是________.
5.物体的运动方程是s=(s的单位:m;t的单位:s),求物体在t=1 s到t=(1+Δt)s这段时间内的平均速度.
学习目标:1.学会通过对一些实例的直观感知,构建平均变化率的概念,并初步运用和加
深理解利用平均变化率来刻画变量变化得快与慢的原理;
2.理解并会求具体函数的平均变化率.
学习重点:了解平均变化率概念的形成过程,会利用平均变化率来刻画变量变化得快与慢.
会在具体的环境中说明平均变化率的实际意义.
学习难点:对平均变化率概念的本质的理解;对生活现象作出数学解释.
【明标自学】预习课本P5-7理清下列概念,完成相应问题。
1.问题情境.
法国《队报》网站的文章称刘翔以不可思议的速度统治了赛场.这名21岁的中国人跑的几乎比炮弹还快.赛道上显示的12.94秒的成绩已经打破了12.95秒的奥运会纪录,但经过验证他是以12.91秒的成绩追平了世界纪录,他的平均速度达到了8.52m/s.
某人走路的第1秒到第34秒的位移时间图象如图所示:
观察图象,回答问题:
问题1 从A到B的位移是多少?从B到C的位移是多少?
问题2 从A到B这一段与从B到C这一段,你感觉哪一段的位移变化得较快?
2.学生活动.
案例中,从B到C位移“陡增”,这是我们从图像中的直观感觉,那么如何量化陡峭程度呢?
(1)由点B上升到C点必须考察的大小,但仅注意到的大小能否精确量化BC段陡峭的程度?为什么?
(2)还必须考察什么量?在考察的同时必须考察.
(3)曲线上BC之间一段几乎成了直线,由此联想到如何量化直线的倾斜程度?
【建构数学】
1.平均变化率:
(1)定义:一般地,函数在区间上的平均变化率为
注意:平均变化率不能脱离区间而言
(2)实质: 的改变量与 的改变量之比.
(3)意义:刻画函数值在区间[x1,x2]上变化的 .
2.平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“视觉化”.
思考:(1)若设,即将看作是对于的一个增量,
则在平均变化率为 .
(2)在平均变化率的几何意义即为 .
【自学检测】
1.在平均变化率的定义中,自变量的增量Δx满足( )
A.Δx<0 B.Δx>0 C.Δx=0 D.Δx≠0
2.设函数y=f(x),当自变量x由x0改变到x0+Δx时,函数值的改变量Δy=( )
A.f(x0+Δx) B.f(x0)+Δx C.f(x0)·Δx D.f(x0+Δx)-f(x0)
3.判断下列命题正确还是错误。
(1)若函数,则在上的平均变化率为.( )
(2)若函数在上的平均变化率小于其在上的平均变化率,所以在上不如在上变化的快.( )
(3)平均变化率不能反映函数值变化的快慢.( )
4.函数在上的平均变化率为________.
【典型例题】
例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到
第3个月以及第6个月到第12个月该婴儿体重的平均变化率.
例2 水经过虹吸管从容器甲流向容器乙,s后容器甲中的水的体积(单位:cm3),试计算第一个10s内的平均变化率.
例3.已知函数,分别计算在区间,上函数及的平均变化率.
思考:从本题的求解中,你能发现一次函数在区间上的平均变化率有什么特点吗?
例4 已知函数,分别计算在下列区间上的平均变化率:
[1,3] ⑤ [0.9,1]
[1,2] ⑥ [0.99,1]
[1,1.1] ⑦ [0.999,1]
[1,1.001] ⑧ [0.9999,1]
思考: 本题中八个区间的变化导致平均变化率有怎样的变化?这种变化的实际意义和数学意义分别是什么?
【当堂检测】
1.函数y=x2+ax+b,当自变量由0变化到1时,函数值的变化量为________.
2.在曲线y=x2+1的图象上取一点(1,2)及相邻的一点(1.1,2.21),则该曲线在[1,1.1]上的平均变化率为________.
3.已知函数f (x)=x2-2x
(1)求f (x)在2到2.1之间的平均变化率.;
(2)求f (x)在x=2到x=2+Δx之间的平均变化率;
(3)求f (x)在x0到x0+Δx之间的平均变化率。
4.为了检测甲、乙两辆车的刹车性能,分别对两辆车进行了测试,甲从25 m/s到0 m/s花了5 s,乙从18 m/s到0 m/s花了4 s,试比较两辆车的刹车性能.
【课堂小结】
【课后作业】
1.已知函数f(x)=2x2-4的图象上一点(1,-2)及邻近一点(1+Δx,-2+Δy),则等于( )
A.4 B.4x C.4+2Δx D.4+2(Δx)2
2.物体做直线运动所经过的路程s可以表示为时间t的函数s=s(t),则物体在时间间隔[t0,t0+Δt]内的平均速度是( )
A.v0 B. C. D.
3.如果质点M按规律s=3+t2运动,则在一小段时间[2,2.1]中相应的平均速度是________(m/s).
4.函数y=sin x在上的平均变化率是________.
5.物体的运动方程是s=(s的单位:m;t的单位:s),求物体在t=1 s到t=(1+Δt)s这段时间内的平均速度.
