2020-2021学年高二下学期数学苏教版选修2-2第一章1.1.2瞬时变化率-导数(1)学案
文档属性
| 名称 | 2020-2021学年高二下学期数学苏教版选修2-2第一章1.1.2瞬时变化率-导数(1)学案 | 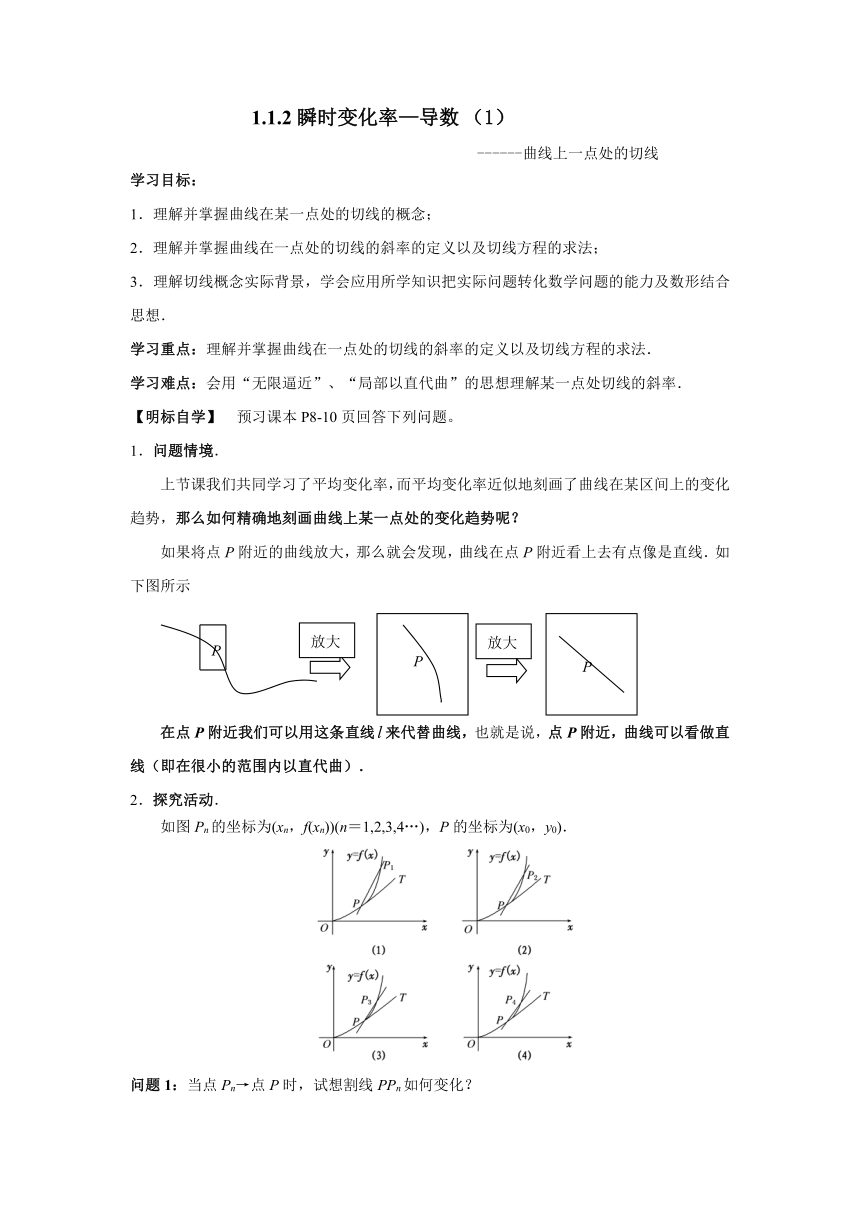 | |
| 格式 | doc | ||
| 文件大小 | 206.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 20:59:13 | ||
图片预览


文档简介
1.1.2瞬时变化率—导数
(1)
------曲线上一点处的切线
学习目标:
1.理解并掌握曲线在某一点处的切线的概念;
2.理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法;
3.理解切线概念实际背景,学会应用所学知识把实际问题转化数学问题的能力及数形结合思想.
学习重点:理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法.
学习难点:会用“无限逼近”、“局部以直代曲”的思想理解某一点处切线的斜率.
【明标自学】
预习课本P8-10页回答下列问题。
1.问题情境.
上节课我们共同学均变化率,而平均变化率近似地刻画了曲线在某区间上的变化趋势,那么如何精确地刻画曲线上某一点处的变化趋势呢?
如果将点P附近的曲线放大,那么就会发现,曲线在点P附近看上去有点像是直线.如下图所示
在点P附近我们可以用这条直线来代替曲线,也就是说,点P附近,曲线可以看做直线(即在很小的范围内以直代曲).
2.探究活动.
如图Pn的坐标为(xn,f(xn))(n=1,2,3,4…),P的坐标为(x0,y0).
问题1:当点Pn→点P时,试想割线PPn如何变化?
问题2:割线PPn斜率是什么?
问题3:割线PPn的斜率与过点P的切线PT的斜率k有什么关系呢?
问题4:能否求得过点P的切线PT的斜率?
【建构数学】
1.割线定义:如图,设Q为曲线C上不同于P的一点,直线PQ称为曲线的
.
2.切线定义:随着点Q沿曲线C向点P运动,割线PQ在点P附近越来越逼近曲线C,当点Q
点P时,直线PQ最终就成为在点P处
曲线的直线l,这条直线l称为曲线在点P处的
.这种方法叫
.
切线的斜率:设曲线上一点,过点的一条割线交曲线于另一点,则割线的斜率
为
,
当点Q沿曲线向点运动,并无限靠近点时,割线逼近点的切线,从而割线的斜率逼近切线的斜率,即当
时,
无限逼近
点处的切线的斜率.
探究:如何求曲线在点处切线的斜率呢?(基本思想:割线逼近切线)
【典型例题】
例1 已知,求曲线在处的切线斜率.
练习 试求在x=1处的切线斜率.
小结:求曲线上一点处的切线斜率的一般步骤:
思考:P为已知曲线C上的一点,如何求出点P处的切线方程?
例2.
已知曲线,
求曲线在点
P(3,9)处的切线方程.
变式:1.曲线
y
2x
2
1在点P(1,3)处的切线方程为
.
2.已知,求曲线在处的切线斜率和切线方程;
3.已知,求曲线在处的切线斜率和切线方程;
【当堂检测】
1.已知,求曲线在处的切线斜率和切线方程.
2.已知,求曲线在处的切线斜率和切线方程.
【课堂小结】
1.曲线上一点P处的切线是过点P的所有直线中最接近P点附近曲线的直线,则P点处的变化趋势可以由该点处的切线反映(局部以直代曲).
2.根据定义,利用割线逼近切线的方法,
可以求出曲线在一点处的切线斜率和方程.
【课后作业】
课本P10,11页练习
曲线上一点处的切线限时练
在曲线上有一点,则该曲线在此点处的切线倾斜角为
.
已知函数
在处的切线斜率为
,则
.
曲线
y
3x
2
1在点处的切线方程为
.
过点且与曲线在点处的切线平行的直线方程为
.
若曲线
y
x
2
-
3x
在点
P
处的切线平行于
x
轴,则点
P
的坐标为
.
已知抛物线在一点处的切线的倾斜角为,则该点的坐标为
.
求曲线
y
-2x
2
2在点
P(1,0)处的切线的斜率及其切线方程.
求曲线
y
x3
-
3x
2
1在点
处的切线方程.
9.分别求在曲线
y
x
2
上过哪一点的切线满足条件:
平行于直线
y
4x
5;
(2)垂直于直线
2x
6
y
5
0
.
10.若曲线
y
x
2
1的一条切线平行于直线
y
4x
3,求这条切线的方程.
(1)
------曲线上一点处的切线
学习目标:
1.理解并掌握曲线在某一点处的切线的概念;
2.理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法;
3.理解切线概念实际背景,学会应用所学知识把实际问题转化数学问题的能力及数形结合思想.
学习重点:理解并掌握曲线在一点处的切线的斜率的定义以及切线方程的求法.
学习难点:会用“无限逼近”、“局部以直代曲”的思想理解某一点处切线的斜率.
【明标自学】
预习课本P8-10页回答下列问题。
1.问题情境.
上节课我们共同学均变化率,而平均变化率近似地刻画了曲线在某区间上的变化趋势,那么如何精确地刻画曲线上某一点处的变化趋势呢?
如果将点P附近的曲线放大,那么就会发现,曲线在点P附近看上去有点像是直线.如下图所示
在点P附近我们可以用这条直线来代替曲线,也就是说,点P附近,曲线可以看做直线(即在很小的范围内以直代曲).
2.探究活动.
如图Pn的坐标为(xn,f(xn))(n=1,2,3,4…),P的坐标为(x0,y0).
问题1:当点Pn→点P时,试想割线PPn如何变化?
问题2:割线PPn斜率是什么?
问题3:割线PPn的斜率与过点P的切线PT的斜率k有什么关系呢?
问题4:能否求得过点P的切线PT的斜率?
【建构数学】
1.割线定义:如图,设Q为曲线C上不同于P的一点,直线PQ称为曲线的
.
2.切线定义:随着点Q沿曲线C向点P运动,割线PQ在点P附近越来越逼近曲线C,当点Q
点P时,直线PQ最终就成为在点P处
曲线的直线l,这条直线l称为曲线在点P处的
.这种方法叫
.
切线的斜率:设曲线上一点,过点的一条割线交曲线于另一点,则割线的斜率
为
,
当点Q沿曲线向点运动,并无限靠近点时,割线逼近点的切线,从而割线的斜率逼近切线的斜率,即当
时,
无限逼近
点处的切线的斜率.
探究:如何求曲线在点处切线的斜率呢?(基本思想:割线逼近切线)
【典型例题】
例1 已知,求曲线在处的切线斜率.
练习 试求在x=1处的切线斜率.
小结:求曲线上一点处的切线斜率的一般步骤:
思考:P为已知曲线C上的一点,如何求出点P处的切线方程?
例2.
已知曲线,
求曲线在点
P(3,9)处的切线方程.
变式:1.曲线
y
2x
2
1在点P(1,3)处的切线方程为
.
2.已知,求曲线在处的切线斜率和切线方程;
3.已知,求曲线在处的切线斜率和切线方程;
【当堂检测】
1.已知,求曲线在处的切线斜率和切线方程.
2.已知,求曲线在处的切线斜率和切线方程.
【课堂小结】
1.曲线上一点P处的切线是过点P的所有直线中最接近P点附近曲线的直线,则P点处的变化趋势可以由该点处的切线反映(局部以直代曲).
2.根据定义,利用割线逼近切线的方法,
可以求出曲线在一点处的切线斜率和方程.
【课后作业】
课本P10,11页练习
曲线上一点处的切线限时练
在曲线上有一点,则该曲线在此点处的切线倾斜角为
.
已知函数
在处的切线斜率为
,则
.
曲线
y
3x
2
1在点处的切线方程为
.
过点且与曲线在点处的切线平行的直线方程为
.
若曲线
y
x
2
-
3x
在点
P
处的切线平行于
x
轴,则点
P
的坐标为
.
已知抛物线在一点处的切线的倾斜角为,则该点的坐标为
.
求曲线
y
-2x
2
2在点
P(1,0)处的切线的斜率及其切线方程.
求曲线
y
x3
-
3x
2
1在点
处的切线方程.
9.分别求在曲线
y
x
2
上过哪一点的切线满足条件:
平行于直线
y
4x
5;
(2)垂直于直线
2x
6
y
5
0
.
10.若曲线
y
x
2
1的一条切线平行于直线
y
4x
3,求这条切线的方程.
