1.1.2导数的概念-2020-2021学年人教A版高中数学选修2-2课件(16张PPT)
文档属性
| 名称 | 1.1.2导数的概念-2020-2021学年人教A版高中数学选修2-2课件(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 236.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览






文档简介
1.1.2 导数的概念
回顾所学物理知识:
既然平均速度不能精确的描述运动员的运动状态,为了更加精确的刻画运动员在某一时刻的运动状态,我们可以考察什么物理量?
一、引入新课
在高台跳水运动中, 运动员在不同时刻的速度是不同的. 我们把物体在某一时刻的速度称为瞬时速度. 平均速度不一定能反映运动员在某一时刻的瞬时速度.
1.瞬时速度
二、新课讲授
又如何求瞬时速度呢? (比如t=2)
平均变化率近似地刻画了曲线在某一区间上的变化趋势.
如何精确地刻画曲线在一点处的变化趋势呢?
根据上面的分析,要想确定2s时的瞬时速度,我们可以先考察t=2附近的情况.
在t=2之前或之后,任意取一个时刻2+Δt,Δt是时间的改变量,可以是正值,也可以是负值,但不为0.
当Δt<0时,2+Δt在2之前;
当Δt>0时,2+Δt在2之后.
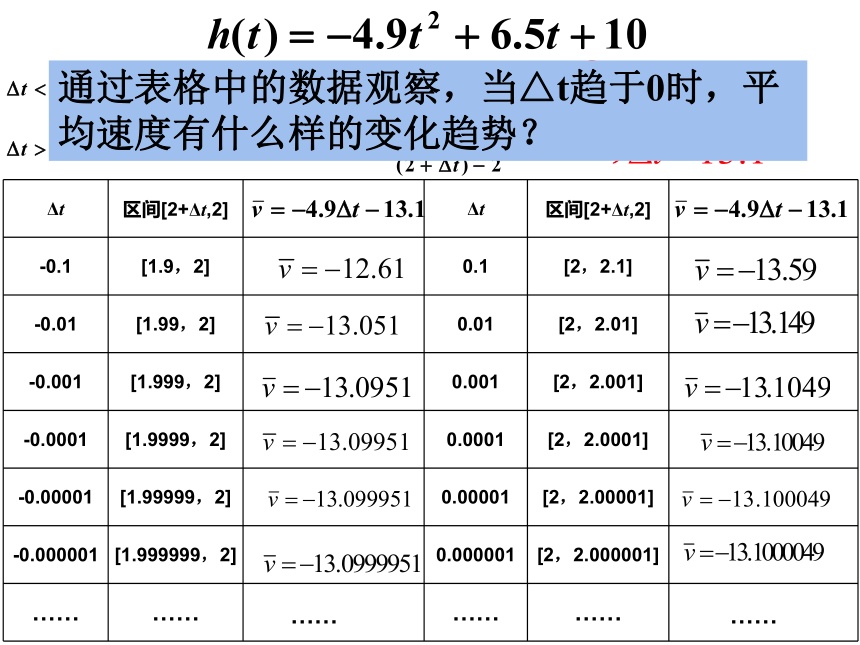
计算区间[2+Δt,2]和区间[2,2+Δt]内平均速度 ,为了方便研究,画表格如下.
?
?
Δt
区间[2+Δt,2]
Δt
区间[2+Δt,2]
-0.1
[1.9,2]
0.1
[2,2.1]
-0.01
[1.99,2]
0.01
[2,2.01]
-0.001
[1.999,2]
0.001
[2,2.001]
-0.0001
[1.9999,2]
0.0001
[2,2.0001]
-0.00001
[1.99999,2]
0.00001
[2,2.00001]
-0.000001
[1.999999,2]
0.000001
[2,2.000001]
……
……
……
……
……
……
通过表格中的数据观察,当△t趋于0时,平均速度有什么样的变化趋势?
当Δt趋近于0时, 即无论t从小于2的一边, 还是从大于2的一边趋近于2时, 平均速度都趋近与一个确定的值 –13.1.
从物理的角度看, 时间间隔|Δt|无限变小时, 平均速度 就无限趋近于t=2时的瞬时速度. 因此, 运动员在t=2时的瞬时速度是 –13.1.
为了表述方便,我们用
表示“当t =2, Δt趋近于0时, 平均速度 趋近于确定值–13.1”.
那么在t=1或t=3时的瞬时速度怎么求?
1. 运动员在某一时刻 t0 的瞬时速度怎样表示?
2. 函数f (x)在 x = x0 处的瞬时变化率怎样表示?
1、探究:
2、定义:
函数y=f(x)在x=x0处的瞬时变化率是
称为函数y=f(x)在x=x0处的导数, 记作f'(x0)或y'|x=x。,
即
(1)y'|x=x。表示函数y关于自变量x在x0处的导数;
(2)f'(x0)与x0的值有关,不同的x0其导数值一般也不相同;
(3)f'(x0)与Δx的具体取值无关;
(4)瞬时变化率与导数是同一概念的两个名称.
二、定义:
函数y=f(x)在x=x0处的瞬时变化率是
称为函数y=f(x)在x=x0处的导数, 记作f'(x0)或y'|x=x。,
即
例1.求函数y=3x2在x=1处的导数.
三、例题讲解
[分析] 利用导数定义求导.
[解析] (1)求y在点x=1处的增量.
Δy=3(1+Δx)2-3×12= 3(Δx)2 +6Δx.
(2)算比值
(3)
由导数的定义可知, 求函数y = f(x)的导数的一般方法:
求函数的改变量
2. 求平均变化率
3.取极限,求导数
简称:一差、二化、三极限
无限逼近的极限思想是建立导数概念、用导数定义求函数的导数的基本思想,丢掉极限思想就无法理解导数概念。
练习1. 求函数f(x) = -x2+x在x = -1附近的平均变化率,并求出在该点处的导数.
练习2. 质点运动规律为s=t2+3,求质点在t=3的瞬时速度.
练习3. 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第xh时, 原油的温度(单位: ℃)为f(x)=x2–7x+15(0≤x≤8) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
解: 在第2h和第6h时, 原油温度的瞬时变化率就是f'(2)和f'(6)
根据导数的定义,
所以,
同理可得
在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3℃/h的速率下降; 在第6h附近,原油温度大约以5℃/h的速率上升.
例4、 物体作自由落体运动,运动方程为: 其中位移单位是m,时间单位是s,g=10m/s2.求:
(1) 物体在时间区间[2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t=2(s)时的瞬时速度.
解:
(1)将Δt=0.1代入上式,得:
(2)将Δt=0.01代入上式,得:
1.求物体运动的瞬时速度:
(1)求位移增量Δs=s(t+Δt)-s(t)
(2)求平均速度
(3)求极限
2.由导数的定义可得求导数的一般步骤:
(1)求函数的增量Δy=f(x0+Δt)-f(x0)
(2)求平均变化率
(3)求极限
四、课堂小结
1、如果质点A按规律s=2t3运动则在t=3s时的瞬时速度为( )
A.6 B.18 C.54 D.81
C
2、已知一个物体运动的位移s(m)与时间t(s)满足关系s(t)=-2t2+5t
(1)求物体第5秒和第6秒的瞬时速度
(2)求物体在t0时刻的瞬时速度
五、课堂练习
回顾所学物理知识:
既然平均速度不能精确的描述运动员的运动状态,为了更加精确的刻画运动员在某一时刻的运动状态,我们可以考察什么物理量?
一、引入新课
在高台跳水运动中, 运动员在不同时刻的速度是不同的. 我们把物体在某一时刻的速度称为瞬时速度. 平均速度不一定能反映运动员在某一时刻的瞬时速度.
1.瞬时速度
二、新课讲授
又如何求瞬时速度呢? (比如t=2)
平均变化率近似地刻画了曲线在某一区间上的变化趋势.
如何精确地刻画曲线在一点处的变化趋势呢?
根据上面的分析,要想确定2s时的瞬时速度,我们可以先考察t=2附近的情况.
在t=2之前或之后,任意取一个时刻2+Δt,Δt是时间的改变量,可以是正值,也可以是负值,但不为0.
当Δt<0时,2+Δt在2之前;
当Δt>0时,2+Δt在2之后.
计算区间[2+Δt,2]和区间[2,2+Δt]内平均速度 ,为了方便研究,画表格如下.
?
?
Δt
区间[2+Δt,2]
Δt
区间[2+Δt,2]
-0.1
[1.9,2]
0.1
[2,2.1]
-0.01
[1.99,2]
0.01
[2,2.01]
-0.001
[1.999,2]
0.001
[2,2.001]
-0.0001
[1.9999,2]
0.0001
[2,2.0001]
-0.00001
[1.99999,2]
0.00001
[2,2.00001]
-0.000001
[1.999999,2]
0.000001
[2,2.000001]
……
……
……
……
……
……
通过表格中的数据观察,当△t趋于0时,平均速度有什么样的变化趋势?
当Δt趋近于0时, 即无论t从小于2的一边, 还是从大于2的一边趋近于2时, 平均速度都趋近与一个确定的值 –13.1.
从物理的角度看, 时间间隔|Δt|无限变小时, 平均速度 就无限趋近于t=2时的瞬时速度. 因此, 运动员在t=2时的瞬时速度是 –13.1.
为了表述方便,我们用
表示“当t =2, Δt趋近于0时, 平均速度 趋近于确定值–13.1”.
那么在t=1或t=3时的瞬时速度怎么求?
1. 运动员在某一时刻 t0 的瞬时速度怎样表示?
2. 函数f (x)在 x = x0 处的瞬时变化率怎样表示?
1、探究:
2、定义:
函数y=f(x)在x=x0处的瞬时变化率是
称为函数y=f(x)在x=x0处的导数, 记作f'(x0)或y'|x=x。,
即
(1)y'|x=x。表示函数y关于自变量x在x0处的导数;
(2)f'(x0)与x0的值有关,不同的x0其导数值一般也不相同;
(3)f'(x0)与Δx的具体取值无关;
(4)瞬时变化率与导数是同一概念的两个名称.
二、定义:
函数y=f(x)在x=x0处的瞬时变化率是
称为函数y=f(x)在x=x0处的导数, 记作f'(x0)或y'|x=x。,
即
例1.求函数y=3x2在x=1处的导数.
三、例题讲解
[分析] 利用导数定义求导.
[解析] (1)求y在点x=1处的增量.
Δy=3(1+Δx)2-3×12= 3(Δx)2 +6Δx.
(2)算比值
(3)
由导数的定义可知, 求函数y = f(x)的导数的一般方法:
求函数的改变量
2. 求平均变化率
3.取极限,求导数
简称:一差、二化、三极限
无限逼近的极限思想是建立导数概念、用导数定义求函数的导数的基本思想,丢掉极限思想就无法理解导数概念。
练习1. 求函数f(x) = -x2+x在x = -1附近的平均变化率,并求出在该点处的导数.
练习2. 质点运动规律为s=t2+3,求质点在t=3的瞬时速度.
练习3. 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第xh时, 原油的温度(单位: ℃)为f(x)=x2–7x+15(0≤x≤8) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
解: 在第2h和第6h时, 原油温度的瞬时变化率就是f'(2)和f'(6)
根据导数的定义,
所以,
同理可得
在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3℃/h的速率下降; 在第6h附近,原油温度大约以5℃/h的速率上升.
例4、 物体作自由落体运动,运动方程为: 其中位移单位是m,时间单位是s,g=10m/s2.求:
(1) 物体在时间区间[2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t=2(s)时的瞬时速度.
解:
(1)将Δt=0.1代入上式,得:
(2)将Δt=0.01代入上式,得:
1.求物体运动的瞬时速度:
(1)求位移增量Δs=s(t+Δt)-s(t)
(2)求平均速度
(3)求极限
2.由导数的定义可得求导数的一般步骤:
(1)求函数的增量Δy=f(x0+Δt)-f(x0)
(2)求平均变化率
(3)求极限
四、课堂小结
1、如果质点A按规律s=2t3运动则在t=3s时的瞬时速度为( )
A.6 B.18 C.54 D.81
C
2、已知一个物体运动的位移s(m)与时间t(s)满足关系s(t)=-2t2+5t
(1)求物体第5秒和第6秒的瞬时速度
(2)求物体在t0时刻的瞬时速度
五、课堂练习
