_2020-2021学年八年级数学人教版下册 第十八章 平行四边形 章末巩固训练(word解析版)
文档属性
| 名称 | _2020-2021学年八年级数学人教版下册 第十八章 平行四边形 章末巩固训练(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 640.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 06:46:32 | ||
图片预览



文档简介
人教版
八年级数学
第十八章
平行四边形
章末巩固训练
一、选择题
1.
以三角形的三个顶点作平行四边形,最多可以作(
)
A.2个
B.3个
C.4个
D.5个
2.
四边形中,、分别是、上的点,、分别是、的中点,当点在上从向移动而点不动时,那么下列结论成立的是
(
)
A.线段的长逐渐增大
B.线段的长逐渐减小
C.线段的长不变
D.线段的长与点的位置有关
3.
(2019·上海)下列命题中,假命题是( )
A.矩形的对角线相等
B.矩形对角线交点到四个顶点的距离相等
C.矩形的对角线互相平
D.矩形对角线交点到四条边的距离相等
4.
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A.
2
B.
4
C.
6
D.
8
5.
如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.
10
B.
14
C.
20
D.
22
6.
(2020·牡丹江)如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,2),将菱形绕点O旋转,当点A落在x轴上时,点C的对应点的坐标为
(
)
A.或
B.
C.
D.或
7.
(2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
8.
(2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是(
)
A.
①②③④
B.
①②③⑤
C.
①②③④⑤
D.
③④⑤
二、填空题
9.
如图,在平行四边中,已知,,平分交边于点,则等于
.
10.
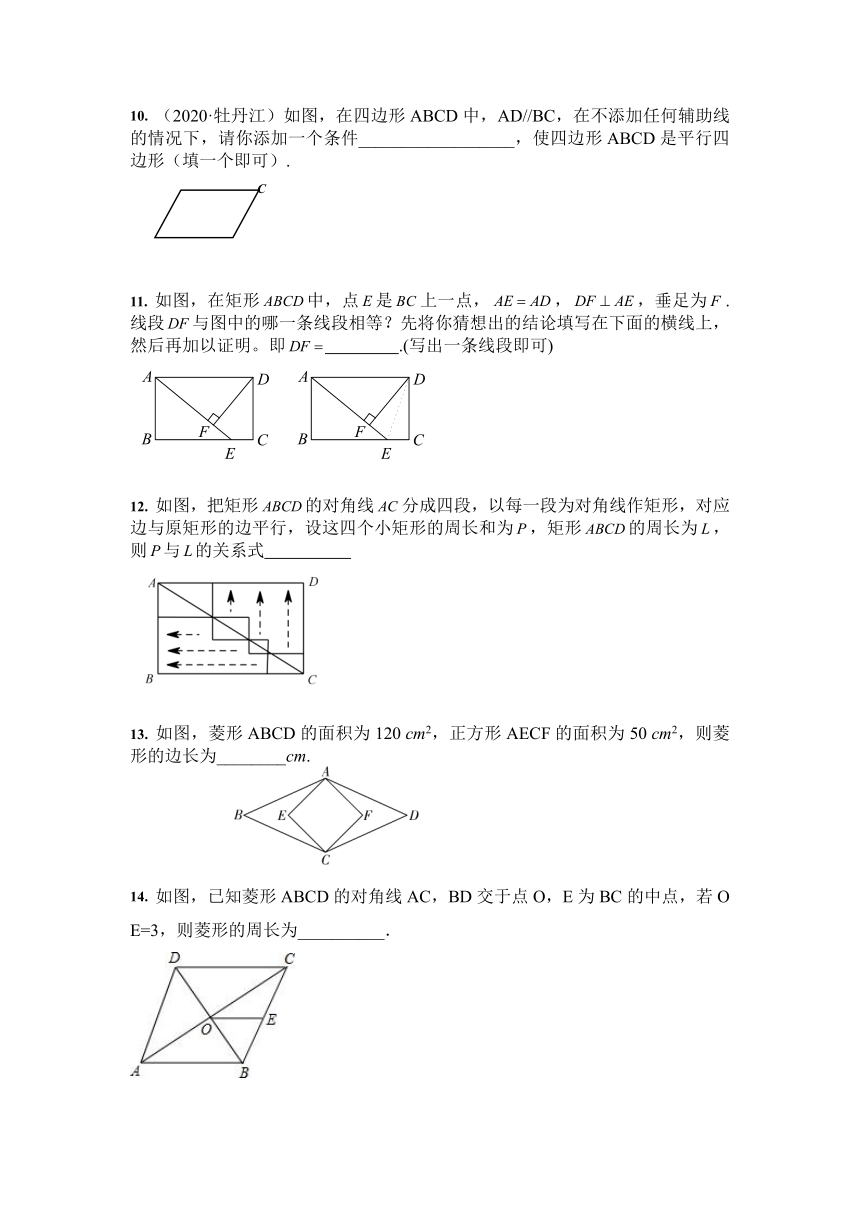
(2020·牡丹江)如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件__________________,使四边形ABCD是平行四边形(填一个即可).
11.
如图,在矩形中,点是上一点,,,垂足为.线段与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明。即
.(写出一条线段即可)
12.
如图,把矩形的对角线分成四段,以每一段为对角线作矩形,对应边与原矩形的边平行,设这四个小矩形的周长和为,矩形的周长为,则与的关系式
13.
如图,菱形ABCD的面积为120
cm2,正方形AECF的面积为50
cm2,则菱形的边长为________cm.
14.
如图,已知菱形ABCD的对角线AC,BD交于点O,E为BC的中点,若OE=3,则菱形的周长为__________.
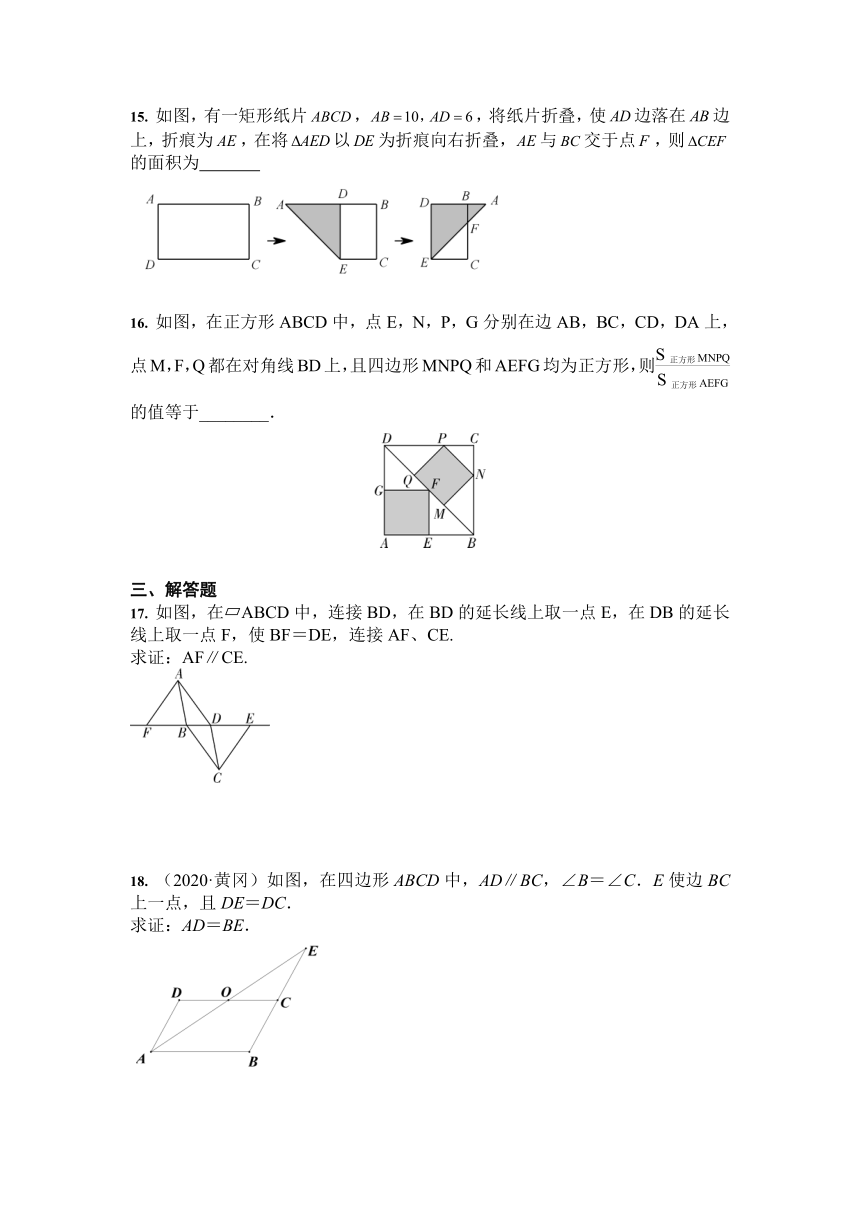
15.
如图,有一矩形纸片,,将纸片折叠,使边落在边上,折痕为,在将以为折痕向右折叠,与交于点,则的面积为
16.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于________.
三、解答题
17.
如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
求证:AF∥CE.
18.
(2020·黄冈)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E使边BC上一点,且DE=DC.
求证:AD=BE.
19.
(2020·陕西)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E使边BC上一点,且DE=DC.求证:AD=BE.
20.
如图,在中,是边上的一点,是的中点,过点作的平行线交的延长线于点,且,连结.
⑴
求证:.
⑵
如果,试判断四边形的形状,并证明你的结论.
21.
以的对边、为边分别在外作等边、等边.求证:
四边形是平行四边形.
22.
如图,平行四边形中,.对角线,相交于点,将直线绕点顺时针旋转,分别交,于点,.
⑴
证明:当旋转角为时,四边形是平行四边形;
⑵
试说明在旋转过程中,线段与总保持相等.
23.
如图所示,在直角梯形中,,,是的垂直平分线,交于点,以腰为边作正方形,作于点,求证.
24.
如图,设正方形的对角线,在延长线上取一点,使,与交于,求证:正方形的边长.
人教版
八年级数学
第十八章
平行四边形
章末巩固训练-答案
一、选择题
1.
【答案】B
2.
【答案】C
【解析】连结,利用三角形的中位线可得与点无关.
3.
【答案】D
【解析】矩形的对角线的交点到每一组对边的距离相等,故选项D错误,是假命题.
4.
【答案】A 【解析】∵E,F
分别是
AD,CD
边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
5.
【答案】B 【解析】∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.由AC+BD=16可得OA+OB=8,又∵AB=CD=6,∴△ABO的周长为OA+OB+AB=8+6=14.
6.
【答案】D
【解析】菱形OABC中,点A的坐标为(2,2),所以OA=4,∠A=∠C=60°,分类讨论,
①若顺时针旋转,旋转后的图形如图1所示,则OC=OA=4,∠C=60°,可求出点C对应点的坐标为(-2,-2);
②若逆时针旋转,旋转后的图形如图2所示,则OC=OA=4,∠C=60°,可求出点C对应点的坐标为(2,2).
7.
【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
8.
【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME=
NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题
9.
【答案】
【解析】∵,,∴.
10.
【答案】AD=BC
【解析】当添加条件AD=BC时,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD是平行四边形.
11.
【答案】.
【解析】连接.
∵四边形是矩形,
∴,,.
∴.
又∵,
∴,
∴,
又∵,
∴≌,
∴.
12.
【答案】.
【解析】如图,将四个小矩形的边分别向外平移,正好拼接成矩形的四边,所以
13.
【答案】13 【解析】如解图,连接AC、BD交于O,则有AC·BD=120,∴AC·BD=240,又∵菱形对角线互相垂直平分,∴2OA·2OB=240,∴
OA·OB=60,∵AE2=50,
OA2+OE2=
AE2,OA=OE,∴OA=5,∴OB=12,∴AB===13.
解图
14.
【答案】24
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=AD,BO=DO,
∵点E是BC的中点,
∴OE是△BCD的中位线,
∴CD=2OE=2×3=6,
∴菱形ABCD的周长=4×6=24;
故答案为:24.
15.
【答案】
【解析】,所以可得面积为
16.
【答案】 【解析】设BD=3a,∠CDB=∠CBD=45°,且四边形PQMN为正方形,∴DQ=PQ=QM=NM=MB,∴正方形MNPQ的边长为a,正方形AEFG的对角线AF=BD=a,∵正方形对角线互相垂直,∴S正方形AEFG=×a×a=a2,∴==.
三、解答题
17.
【答案】
证明:∵四边形ABCD是平行四边形,
解图
∴AD∥BC,AD=BC,
∴∠1=∠2,
又∵BF=DE,(1分)
∴BF+BD=DE+BD,
即DF=BE.(2分)
∴△ADF≌△CBE(SAS).(3分)
∴∠AFD=∠CEB,
∴AF∥CE.(5分)
18.
【答案】
解:∵□ABCD,∴∠AD=∠BC,∴∠C=∠DAO.
∵点O为CD的中点,∴DO=∠CO.又∵∠AOD=∠EOC,∴△AOD≌△EOC.∴AD=CE.
19.
【答案】
解:∵DE=DC,∴∠C=∠DEC.∵∠B=∠C,∴∠B=∠DEC,
∴AB∥DE.∵AD∥BC,∴四边形ABED为平行四边形,∴AD=BE.
20.
【答案】
⑴
∵,
是的中点,∴
∵
∴
∴,∵
∴
(2)四边形是矩形
∵,是的中点(利用全等)
∴
∴
∵,
∴四边形是平行四边形
又
∴四边形是矩形.
21.
【答案】
∵,和都是等边三角形
∴,
∵,,
∴,∴≌
∴,∴四边形是平行四边形
22.
【答案】
⑴
证明:当时,,
又∵,
∴四边形为平行四边形.
⑵
证明:四边形为平行四边形
∴,,
∴
∴
23.
【答案】
直接证明不太可行,可转化成证明,而,故进而考虑到将、集中到一条线段上,然后将也平移过来.
我们将视线集中在正方形之中,通过可以得证.
过点作的垂线,过作的垂线,垂足分别为、,
则有为矩形,..
又因为,所以.
所以
24.
【答案】
当且仅当为直角三角形时,的中线.
由已知证明为直角三角形并不困难.
因为为正方形,所以.由于,所以.
又,
所以.
从而.
因为,所以(即),
.
故为直角三角形,且为斜边的中线,从而
正方形的边长.
BV
OV
CV
AV
x
y
D
A
B
C
图2
图1
y
x
AV
BV
CV
OV
y
x
AV
BV
CV
OV
八年级数学
第十八章
平行四边形
章末巩固训练
一、选择题
1.
以三角形的三个顶点作平行四边形,最多可以作(
)
A.2个
B.3个
C.4个
D.5个
2.
四边形中,、分别是、上的点,、分别是、的中点,当点在上从向移动而点不动时,那么下列结论成立的是
(
)
A.线段的长逐渐增大
B.线段的长逐渐减小
C.线段的长不变
D.线段的长与点的位置有关
3.
(2019·上海)下列命题中,假命题是( )
A.矩形的对角线相等
B.矩形对角线交点到四个顶点的距离相等
C.矩形的对角线互相平
D.矩形对角线交点到四条边的距离相等
4.
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A.
2
B.
4
C.
6
D.
8
5.
如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.
10
B.
14
C.
20
D.
22
6.
(2020·牡丹江)如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,2),将菱形绕点O旋转,当点A落在x轴上时,点C的对应点的坐标为
(
)
A.或
B.
C.
D.或
7.
(2019?广西池河)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是
A.∠B=∠F
B.∠B=∠BCF
C.AC=CF
D.AD=CF
8.
(2020·东营)如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N,下列结论:①△APE≌△AME;②PM+PN=AC;③;④△POF∽△BNF;⑤点O在M、N两点的连线上.其中正确的是(
)
A.
①②③④
B.
①②③⑤
C.
①②③④⑤
D.
③④⑤
二、填空题
9.
如图,在平行四边中,已知,,平分交边于点,则等于
.
10.
(2020·牡丹江)如图,在四边形ABCD中,AD//BC,在不添加任何辅助线的情况下,请你添加一个条件__________________,使四边形ABCD是平行四边形(填一个即可).
11.
如图,在矩形中,点是上一点,,,垂足为.线段与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明。即
.(写出一条线段即可)
12.
如图,把矩形的对角线分成四段,以每一段为对角线作矩形,对应边与原矩形的边平行,设这四个小矩形的周长和为,矩形的周长为,则与的关系式
13.
如图,菱形ABCD的面积为120
cm2,正方形AECF的面积为50
cm2,则菱形的边长为________cm.
14.
如图,已知菱形ABCD的对角线AC,BD交于点O,E为BC的中点,若OE=3,则菱形的周长为__________.
15.
如图,有一矩形纸片,,将纸片折叠,使边落在边上,折痕为,在将以为折痕向右折叠,与交于点,则的面积为
16.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则的值等于________.
三、解答题
17.
如图,在?ABCD中,连接BD,在BD的延长线上取一点E,在DB的延长线上取一点F,使BF=DE,连接AF、CE.
求证:AF∥CE.
18.
(2020·黄冈)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E使边BC上一点,且DE=DC.
求证:AD=BE.
19.
(2020·陕西)如图,在四边形ABCD中,AD∥BC,∠B=∠C.E使边BC上一点,且DE=DC.求证:AD=BE.
20.
如图,在中,是边上的一点,是的中点,过点作的平行线交的延长线于点,且,连结.
⑴
求证:.
⑵
如果,试判断四边形的形状,并证明你的结论.
21.
以的对边、为边分别在外作等边、等边.求证:
四边形是平行四边形.
22.
如图,平行四边形中,.对角线,相交于点,将直线绕点顺时针旋转,分别交,于点,.
⑴
证明:当旋转角为时,四边形是平行四边形;
⑵
试说明在旋转过程中,线段与总保持相等.
23.
如图所示,在直角梯形中,,,是的垂直平分线,交于点,以腰为边作正方形,作于点,求证.
24.
如图,设正方形的对角线,在延长线上取一点,使,与交于,求证:正方形的边长.
人教版
八年级数学
第十八章
平行四边形
章末巩固训练-答案
一、选择题
1.
【答案】B
2.
【答案】C
【解析】连结,利用三角形的中位线可得与点无关.
3.
【答案】D
【解析】矩形的对角线的交点到每一组对边的距离相等,故选项D错误,是假命题.
4.
【答案】A 【解析】∵E,F
分别是
AD,CD
边上的中点,即EF是△ACD的中位线,∴AC=2EF=2,则菱形ABCD的面积=AC·BD=×2×2=2.
5.
【答案】B 【解析】∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.由AC+BD=16可得OA+OB=8,又∵AB=CD=6,∴△ABO的周长为OA+OB+AB=8+6=14.
6.
【答案】D
【解析】菱形OABC中,点A的坐标为(2,2),所以OA=4,∠A=∠C=60°,分类讨论,
①若顺时针旋转,旋转后的图形如图1所示,则OC=OA=4,∠C=60°,可求出点C对应点的坐标为(-2,-2);
②若逆时针旋转,旋转后的图形如图2所示,则OC=OA=4,∠C=60°,可求出点C对应点的坐标为(2,2).
7.
【答案】B
【解析】∵在△ABC中,D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,∴DEAC.
A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.
C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.
故选B.
8.
【答案】B
【解析】本题考查了垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质,是常见问题的综合,灵活的运用所学知识是解答本题的关键.综合应用垂线、平行线和正方形的性质,全等三角形的判定与性质、等腰直角三角形的判断和性质、相似三角形的判定和性质等知识,逐个判断5个结论的正确性,得出结论.
①∵正方形ABCD,∴∠APE=∠AME=45°,∵PM⊥AE,∴∠AEP=∠AEM=90°,∵AE=AE,∴△APE≌△AME(ASA);
②过点N作NQ⊥AC于点Q,则四边形PNQE是矩形,∴PN=EQ,∵正方形ABCD,∴∠PAE=∠MAE=45°,∵PM⊥AE,∴∠PEA=45°,∴∠PAE=∠APE,PE=NQ,∴△APE等腰直角三角形,∴AE=PE,同理得:△NQC等腰直角三角形,∴NQ=CQ,∵△APE≌△AME,∴PE=ME,∴PE=ME=
NQ=CQ,∴PM=AE+CQ,∴PM+PN=AE+CQ+EQ=AC,即PM+PN=AC成立;
③∵正方形ABCD,∴AC⊥BD,∴∠EOF是直角,∵过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,∴∠PEO和∠PFO是直角,∴四边形PFOE是矩形,∴PF=OE,在Rt△PEO中,有PE2+OE2=PO2,∴PE2+PF2=PO2,即PE2+PF2=PO2成立;
④△BNF是等腰直角三角形,点P不在AB的中点时,△POF不是等腰直角三角形,所以△POF与△BNF不一定相似,即△POF∽△BNF不一定成立;
⑤∵△AMP是等腰直角三角形,△PMN∽△AMP,∴△PMN是等腰直角三角形,∵∠MPN=90°,∴PM=PN,∵AP=PM,BP=PN,∴AP=BP,∴点P是AB的中点,又∵O为正方形的对称中点,∴点O在M、N两点的连线上.综上,①②③⑤成立,即正确的结论有4个,答案选B.
二、填空题
9.
【答案】
【解析】∵,,∴.
10.
【答案】AD=BC
【解析】当添加条件AD=BC时,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD是平行四边形.
11.
【答案】.
【解析】连接.
∵四边形是矩形,
∴,,.
∴.
又∵,
∴,
∴,
又∵,
∴≌,
∴.
12.
【答案】.
【解析】如图,将四个小矩形的边分别向外平移,正好拼接成矩形的四边,所以
13.
【答案】13 【解析】如解图,连接AC、BD交于O,则有AC·BD=120,∴AC·BD=240,又∵菱形对角线互相垂直平分,∴2OA·2OB=240,∴
OA·OB=60,∵AE2=50,
OA2+OE2=
AE2,OA=OE,∴OA=5,∴OB=12,∴AB===13.
解图
14.
【答案】24
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=AD,BO=DO,
∵点E是BC的中点,
∴OE是△BCD的中位线,
∴CD=2OE=2×3=6,
∴菱形ABCD的周长=4×6=24;
故答案为:24.
15.
【答案】
【解析】,所以可得面积为
16.
【答案】 【解析】设BD=3a,∠CDB=∠CBD=45°,且四边形PQMN为正方形,∴DQ=PQ=QM=NM=MB,∴正方形MNPQ的边长为a,正方形AEFG的对角线AF=BD=a,∵正方形对角线互相垂直,∴S正方形AEFG=×a×a=a2,∴==.
三、解答题
17.
【答案】
证明:∵四边形ABCD是平行四边形,
解图
∴AD∥BC,AD=BC,
∴∠1=∠2,
又∵BF=DE,(1分)
∴BF+BD=DE+BD,
即DF=BE.(2分)
∴△ADF≌△CBE(SAS).(3分)
∴∠AFD=∠CEB,
∴AF∥CE.(5分)
18.
【答案】
解:∵□ABCD,∴∠AD=∠BC,∴∠C=∠DAO.
∵点O为CD的中点,∴DO=∠CO.又∵∠AOD=∠EOC,∴△AOD≌△EOC.∴AD=CE.
19.
【答案】
解:∵DE=DC,∴∠C=∠DEC.∵∠B=∠C,∴∠B=∠DEC,
∴AB∥DE.∵AD∥BC,∴四边形ABED为平行四边形,∴AD=BE.
20.
【答案】
⑴
∵,
是的中点,∴
∵
∴
∴,∵
∴
(2)四边形是矩形
∵,是的中点(利用全等)
∴
∴
∵,
∴四边形是平行四边形
又
∴四边形是矩形.
21.
【答案】
∵,和都是等边三角形
∴,
∵,,
∴,∴≌
∴,∴四边形是平行四边形
22.
【答案】
⑴
证明:当时,,
又∵,
∴四边形为平行四边形.
⑵
证明:四边形为平行四边形
∴,,
∴
∴
23.
【答案】
直接证明不太可行,可转化成证明,而,故进而考虑到将、集中到一条线段上,然后将也平移过来.
我们将视线集中在正方形之中,通过可以得证.
过点作的垂线,过作的垂线,垂足分别为、,
则有为矩形,..
又因为,所以.
所以
24.
【答案】
当且仅当为直角三角形时,的中线.
由已知证明为直角三角形并不困难.
因为为正方形,所以.由于,所以.
又,
所以.
从而.
因为,所以(即),
.
故为直角三角形,且为斜边的中线,从而
正方形的边长.
BV
OV
CV
AV
x
y
D
A
B
C
图2
图1
y
x
AV
BV
CV
OV
y
x
AV
BV
CV
OV
