2020-2021学年八年级数学人教版下册 19.2.3 一次函数与方程、不等式课件(29张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 19.2.3 一次函数与方程、不等式课件(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 11:16:46 | ||
图片预览





文档简介
(共29张PPT)
19.2.3一次函数与方程、不等式
人教版八年级数学下册
学习目标
1.理解一次函数与一元一次方程、一元一次不等式、二元一次方程组的关系。
2.会用数形结合的方法分析和解决问题。
探究问题一
画出一次函数y=2x+1的图像,并观察图像,解决以下问题:
1.求函数图像与x轴交点坐标。
2.判断x取什么值时y=0.
3.函数y=2x+1的图像与x轴的交点横坐标与一元一次方程2x+1=0的解有何关系?
解答
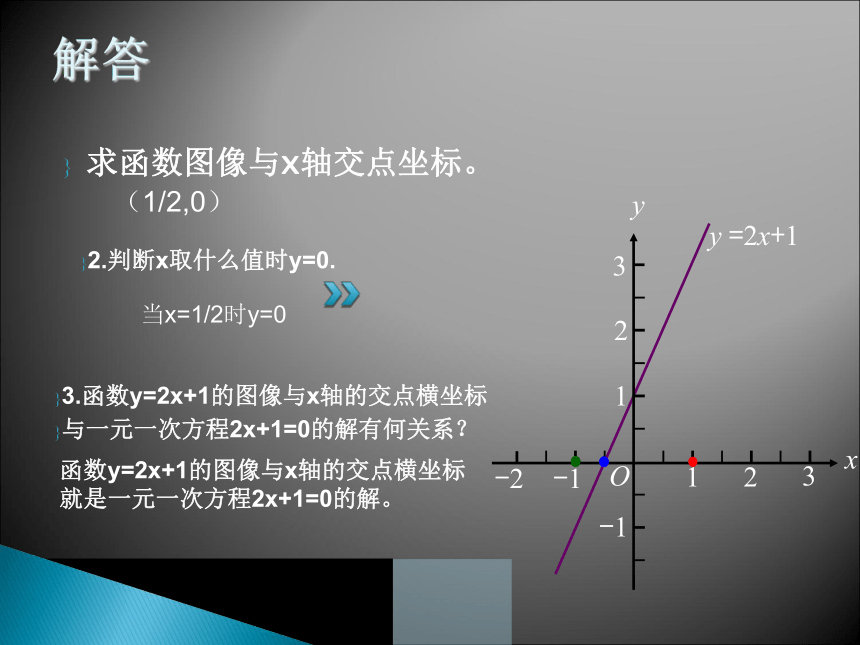
求函数图像与x轴交点坐标。
y
=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
(1/2,0)
2.判断x取什么值时y=0.
3.函数y=2x+1的图像与x轴的交点横坐标
与一元一次方程2x+1=0的解有何关系?
当x=1/2时y=0
函数y=2x+1的图像与x轴的交点横坐标
就是一元一次方程2x+1=0的解。
探究问题一
画出一次函数y=2x+1的图像,并观察图像,解决以下问题:
1。求函数图像与y=3交点坐标。
2.判断x取什么值时y=0.
3.函数y=2x+1的图像与x轴的交点横坐标与一元一次方程2x+1=0的解有何关系?
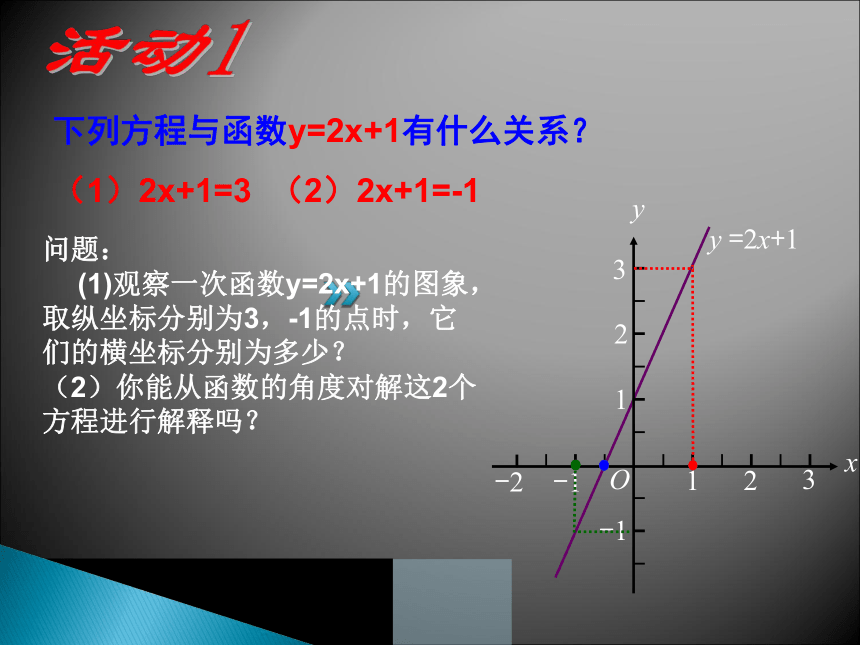
下列方程与函数y=2x+1有什么关系?
(1)2x+1=3
(2)2x+1=-1
y
=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题:
(1)观察一次函数y=2x+1的图象,取纵坐标分别为3,-1的点时,它们的横坐标分别为多少?
(2)你能从函数的角度对解这2个方程进行解释吗?
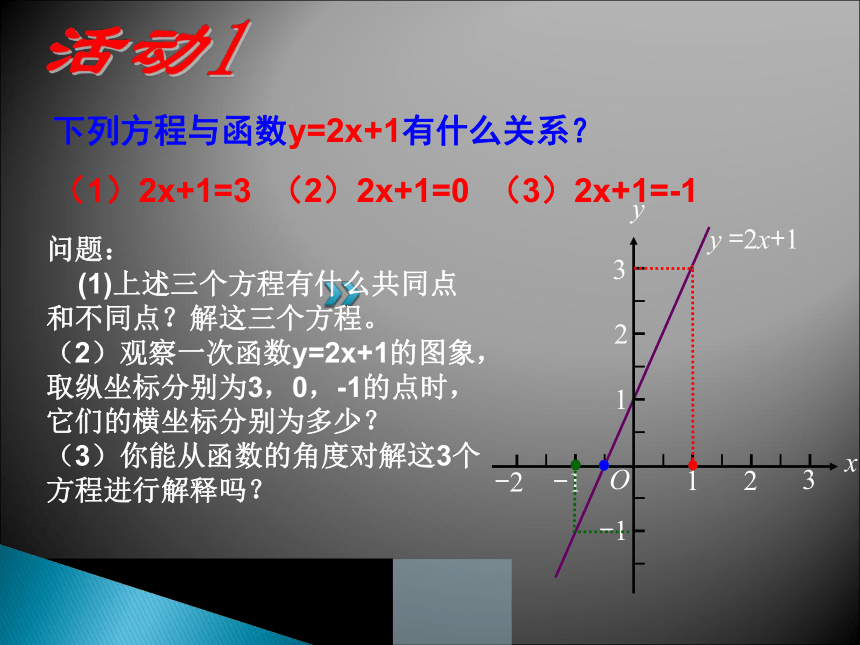
下列方程与函数y=2x+1有什么关系?
(1)2x+1=3
(2)2x+1=0
(3)2x+1=-1
y
=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题:
(1)上述三个方程有什么共同点和不同点?解这三个方程。
(2)观察一次函数y=2x+1的图象,取纵坐标分别为3,0,-1的点时,它们的横坐标分别为多少?
(3)你能从函数的角度对解这3个方程进行解释吗?
从“数”上看
序号
一元一次方程问题
一次函数问题
1
2
3
解方程
2x+1=-1
4
解方程ax+b=0
解方程
2x+1=0
解方程
2x+1=3
函数y=2x+1的值为3时对应的自变量X值
函数y=2x+1的值为0时对应的自变量X值
函数y=2x+1的值为-1时对应的自变量X的值
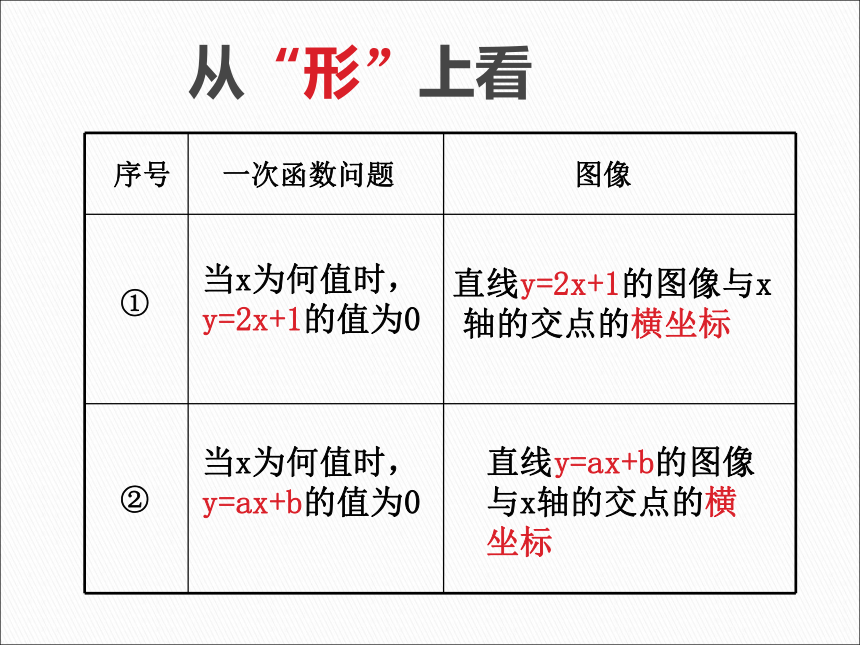
从“形”上看
直线y=2x+1的图像与x轴的交点的横坐标
序号
一次函数问题
图像
①
②
当x为何值时,y=2x+1的值为0
当x为何值时,y=ax+b的值为0
直线y=ax+b的图像与x轴的交点的横坐标
面对问题:
(1)解方程2x+1=0
(2)当自变量x为何值时,函数y=2x+1的值为0?
结论:这两个问题实际上是同一个问题(只是表达形式不同)
求ax+b=0(a,
b是
常数,a≠0)的解
当X为何值时
y=
ax+b的值为0
求直线y=
ax+b
与X轴交点的横坐标
从“数”的角度看
从“形”的角度看
求ax+b=0(a,
b是
常数,a≠0)的解
规律总结
一次函数与一元一次方程的关系
一般地,一元一次方程ax+b=0的解就是函数y=ax+b的图像与x轴交点的横坐标。
针对练习
1、已知:一次函数y=0.8x-2与x轴的交点为(2.5,0),你能说出0.8x-2=0的解吗?
2、已知:一次函数y=ax-5与x轴的交点为(3,0),那么你能说出ax-5=0的解吗?
针对练习
1、已知一次函数y=-2x+2,根据图像回答
(1)当y=0时,求x的值;
(2)当y=2时,求x的值
3
2
1
2
1
-2
O
x
y
-1
-1
3
解:
(1)由图像可知:一次函数y=-2x+2与x轴的交点为(1,0)∴当y=0时,x=1
(2)由图像可知:一次函数y=-2x+2与y轴的交点为(0,2)∴当y=2时,x=0
2.
已知方程ax+b=0的解是-2,下列图象肯定不是直线
y=ax+b的是(
)
x
y
0
-2
(
C
)
(
D
)
x
y
0
-2
x
y
0
-2
(
B
)
x
y
0
-2
-2
(
A
)
B
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y
=3x+2
不等式ax+b>0(a≠0)的解集是函数y=ax+b的图象在x轴上方的部分所对应的x的取值范围.
根据一次函数y=
3x+2
的图像,你能说出一元一次不等式
3x+2<0的解集吗?
3
2
1
2
1
-2
O
x
y
-1
-1
3
y
=3x+2
分析:函数y=
3x+2
的函数值y<0,此时函数图像位于x轴的下方,它的自变量取值范围为x<-2/3.
所以3x+2<0的解集为x<-2/3
根据一次函数y=
3x+2
的图像,你能说出一元一次不等式
3x+2>2的解集吗?
3
2
1
2
1
-2
O
x
y
-1
-1
3
y
=3x+2
分析:函数y=
3x+2
的函数值y>2,此时函数图像位于x轴的下方,它的自变量取值范围为x<-2/3.
所以3x+2>2的解集为x>0
求ax+b>0
(或<0)的解
X为何值时,
y=
ax+b的值大于0
(或小于0)
求直线y=
ax+b在X轴
上方(或下方)部分
所有点的横坐标
从数的角度看
从形的角度看
一次函数与一元一次不等式的关系
求ax+b>0
(或<0)的解
归纳
练一练
1、直线y=mx+n与x轴的交点坐标是(2,0)不等式mx+n<0的解集是
。
x
o
y
2
y=mx+n
x>2
2、当x
时,直线y=-x+2上的点在x轴的下方。
>2
x
o
y
2
2
2题图
1题图
练一练
3、一次函数y=kx+b的图像如图,你能说出
kx+b<0的解集吗?
3
2
1
2
1
-2
O
x
y
-1
-1
3
思考:
二元一次
方程组与一次函数的关系
任何一个方程组都可以看成是两个一次函数的组合.
对于①,根据方程组解的意义和函数的观点,就是求当x取什么数值时,两个—次函数的y值相等?它反映在图象上,就是求直线y=-0.6x+1.6和直线y=2x-1的交点坐标.
①
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=2x+1
y
=3x+2
直角坐标系中两直线的交点的坐标
可以看作是一个二元一次方程组的解。
方程组的解.就是这两个函数表达式组成的两一次函数的图象的交点坐标
归纳
你一定能行的!
巩固练习
做
一
做
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组
的解为
.
2、若二元一次方程组
的解为
,
则函数
与
的图象的交点坐标为
.
(2,2)
一、今天学习了什么?
二、有什么疑问的地方?
三、有什么和老师、同学探讨的吗?
收获
当堂检测
1.直线y=-x+5与x轴的交点坐标为(5,0)则方程5-x=0的解是x=
____
2.直线y=kx-3与x轴的交点是(-1,0),则kx=3的解是x
=
____
3.直线y=-x+2与x轴的交点是(2,0)
,0
则不等式-x+2>0的解集是
.
x<
_____
4.方程组
的解为
;所以点(-1,1)是直线____
与直线_____的交点.
兴趣是最好的老师
布置作业
A:教材99至100页11题,13题,15题(前20名)
B:教材99页11题,13题
www..cn
再见
19.2.3一次函数与方程、不等式
人教版八年级数学下册
学习目标
1.理解一次函数与一元一次方程、一元一次不等式、二元一次方程组的关系。
2.会用数形结合的方法分析和解决问题。
探究问题一
画出一次函数y=2x+1的图像,并观察图像,解决以下问题:
1.求函数图像与x轴交点坐标。
2.判断x取什么值时y=0.
3.函数y=2x+1的图像与x轴的交点横坐标与一元一次方程2x+1=0的解有何关系?
解答
求函数图像与x轴交点坐标。
y
=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
(1/2,0)
2.判断x取什么值时y=0.
3.函数y=2x+1的图像与x轴的交点横坐标
与一元一次方程2x+1=0的解有何关系?
当x=1/2时y=0
函数y=2x+1的图像与x轴的交点横坐标
就是一元一次方程2x+1=0的解。
探究问题一
画出一次函数y=2x+1的图像,并观察图像,解决以下问题:
1。求函数图像与y=3交点坐标。
2.判断x取什么值时y=0.
3.函数y=2x+1的图像与x轴的交点横坐标与一元一次方程2x+1=0的解有何关系?
下列方程与函数y=2x+1有什么关系?
(1)2x+1=3
(2)2x+1=-1
y
=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题:
(1)观察一次函数y=2x+1的图象,取纵坐标分别为3,-1的点时,它们的横坐标分别为多少?
(2)你能从函数的角度对解这2个方程进行解释吗?
下列方程与函数y=2x+1有什么关系?
(1)2x+1=3
(2)2x+1=0
(3)2x+1=-1
y
=2x+1
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题:
(1)上述三个方程有什么共同点和不同点?解这三个方程。
(2)观察一次函数y=2x+1的图象,取纵坐标分别为3,0,-1的点时,它们的横坐标分别为多少?
(3)你能从函数的角度对解这3个方程进行解释吗?
从“数”上看
序号
一元一次方程问题
一次函数问题
1
2
3
解方程
2x+1=-1
4
解方程ax+b=0
解方程
2x+1=0
解方程
2x+1=3
函数y=2x+1的值为3时对应的自变量X值
函数y=2x+1的值为0时对应的自变量X值
函数y=2x+1的值为-1时对应的自变量X的值
从“形”上看
直线y=2x+1的图像与x轴的交点的横坐标
序号
一次函数问题
图像
①
②
当x为何值时,y=2x+1的值为0
当x为何值时,y=ax+b的值为0
直线y=ax+b的图像与x轴的交点的横坐标
面对问题:
(1)解方程2x+1=0
(2)当自变量x为何值时,函数y=2x+1的值为0?
结论:这两个问题实际上是同一个问题(只是表达形式不同)
求ax+b=0(a,
b是
常数,a≠0)的解
当X为何值时
y=
ax+b的值为0
求直线y=
ax+b
与X轴交点的横坐标
从“数”的角度看
从“形”的角度看
求ax+b=0(a,
b是
常数,a≠0)的解
规律总结
一次函数与一元一次方程的关系
一般地,一元一次方程ax+b=0的解就是函数y=ax+b的图像与x轴交点的横坐标。
针对练习
1、已知:一次函数y=0.8x-2与x轴的交点为(2.5,0),你能说出0.8x-2=0的解吗?
2、已知:一次函数y=ax-5与x轴的交点为(3,0),那么你能说出ax-5=0的解吗?
针对练习
1、已知一次函数y=-2x+2,根据图像回答
(1)当y=0时,求x的值;
(2)当y=2时,求x的值
3
2
1
2
1
-2
O
x
y
-1
-1
3
解:
(1)由图像可知:一次函数y=-2x+2与x轴的交点为(1,0)∴当y=0时,x=1
(2)由图像可知:一次函数y=-2x+2与y轴的交点为(0,2)∴当y=2时,x=0
2.
已知方程ax+b=0的解是-2,下列图象肯定不是直线
y=ax+b的是(
)
x
y
0
-2
(
C
)
(
D
)
x
y
0
-2
x
y
0
-2
(
B
)
x
y
0
-2
-2
(
A
)
B
下面三个不等式有什么共同特点?你能从函
数的角度对解这三个不等式进行解释吗?
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
3
2
1
2
1
-2
O
x
y
-1
-1
3
y
=3x+2
不等式ax+b>0(a≠0)的解集是函数y=ax+b的图象在x轴上方的部分所对应的x的取值范围.
根据一次函数y=
3x+2
的图像,你能说出一元一次不等式
3x+2<0的解集吗?
3
2
1
2
1
-2
O
x
y
-1
-1
3
y
=3x+2
分析:函数y=
3x+2
的函数值y<0,此时函数图像位于x轴的下方,它的自变量取值范围为x<-2/3.
所以3x+2<0的解集为x<-2/3
根据一次函数y=
3x+2
的图像,你能说出一元一次不等式
3x+2>2的解集吗?
3
2
1
2
1
-2
O
x
y
-1
-1
3
y
=3x+2
分析:函数y=
3x+2
的函数值y>2,此时函数图像位于x轴的下方,它的自变量取值范围为x<-2/3.
所以3x+2>2的解集为x>0
求ax+b>0
(或<0)的解
X为何值时,
y=
ax+b的值大于0
(或小于0)
求直线y=
ax+b在X轴
上方(或下方)部分
所有点的横坐标
从数的角度看
从形的角度看
一次函数与一元一次不等式的关系
求ax+b>0
(或<0)的解
归纳
练一练
1、直线y=mx+n与x轴的交点坐标是(2,0)不等式mx+n<0的解集是
。
x
o
y
2
y=mx+n
x>2
2、当x
时,直线y=-x+2上的点在x轴的下方。
>2
x
o
y
2
2
2题图
1题图
练一练
3、一次函数y=kx+b的图像如图,你能说出
kx+b<0的解集吗?
3
2
1
2
1
-2
O
x
y
-1
-1
3
思考:
二元一次
方程组与一次函数的关系
任何一个方程组都可以看成是两个一次函数的组合.
对于①,根据方程组解的意义和函数的观点,就是求当x取什么数值时,两个—次函数的y值相等?它反映在图象上,就是求直线y=-0.6x+1.6和直线y=2x-1的交点坐标.
①
3
2
1
2
1
-2
O
x
y
-1
-1
3
y=2x+1
y
=3x+2
直角坐标系中两直线的交点的坐标
可以看作是一个二元一次方程组的解。
方程组的解.就是这两个函数表达式组成的两一次函数的图象的交点坐标
归纳
你一定能行的!
巩固练习
做
一
做
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组
的解为
.
2、若二元一次方程组
的解为
,
则函数
与
的图象的交点坐标为
.
(2,2)
一、今天学习了什么?
二、有什么疑问的地方?
三、有什么和老师、同学探讨的吗?
收获
当堂检测
1.直线y=-x+5与x轴的交点坐标为(5,0)则方程5-x=0的解是x=
____
2.直线y=kx-3与x轴的交点是(-1,0),则kx=3的解是x
=
____
3.直线y=-x+2与x轴的交点是(2,0)
,0
则不等式-x+2>0的解集是
.
x<
_____
4.方程组
的解为
;所以点(-1,1)是直线____
与直线_____的交点.
兴趣是最好的老师
布置作业
A:教材99至100页11题,13题,15题(前20名)
B:教材99页11题,13题
www..cn
再见
