2020-2021学年七年级数学人教版下册9.3一元一次不等式组(第二课时)(共36张PPT)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册9.3一元一次不等式组(第二课时)(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 915.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 11:21:49 | ||
图片预览









文档简介
(共36张PPT)
第九章
不等式与不等式组
9.3
一元一次不等
式组(2)
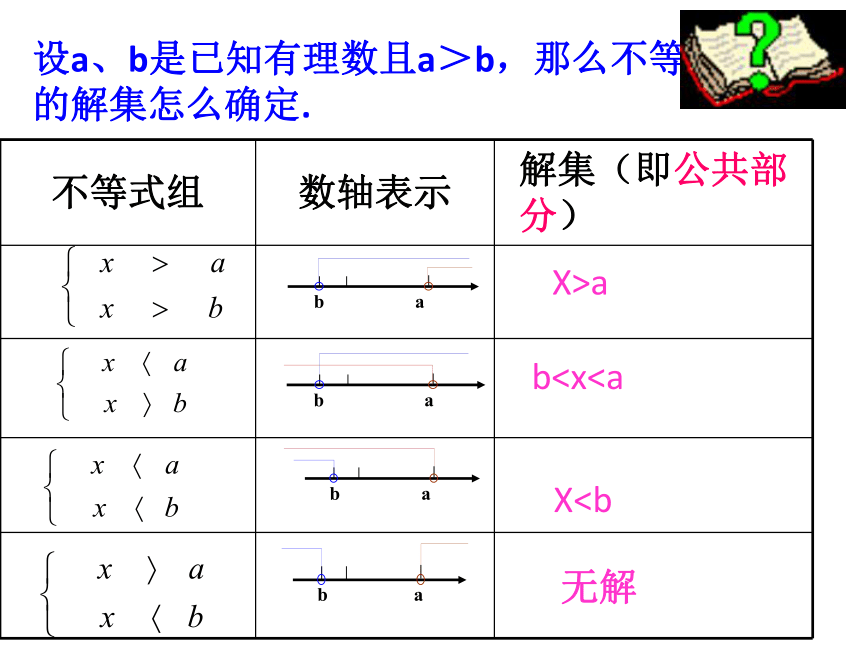
设a、b是已知有理数且a>b,那么不等式组的解集怎么确定.
不等式组
数轴表示
解集(即公共部分)
b
a
b
a
b
a
b
a
无解
X>a
bX“不能完成任务”的意思是:按原先的生产速度,
10天的产品数量
500;
“提前完成任务”的意思是:提高速度后,10天
的产品的数量
500.
3个小组计划在10
天内生产500件产品(每天生产量相同),按原计划的生产速度,不能完成生产任务;如果每个小组比原先多生产1件产品,就能提前完成任务。每个小组原先每天生产多少件?
典例探究
小于
大于
你能找出不等关系吗?
你能列出不等式组了吗?
解:设每个小组原先每天生产X件产品
,则提高速度后每天生产(X+1)
件产品
。根据题中前后两个条件,
得
3?×
10X
<
500
3
×10(X+1)>
500
(1)
(2)
根据题意,
X的值应是整数,所以X=16
答:每个小组原先每天生产16件产品。
解得:15
<
X
<16
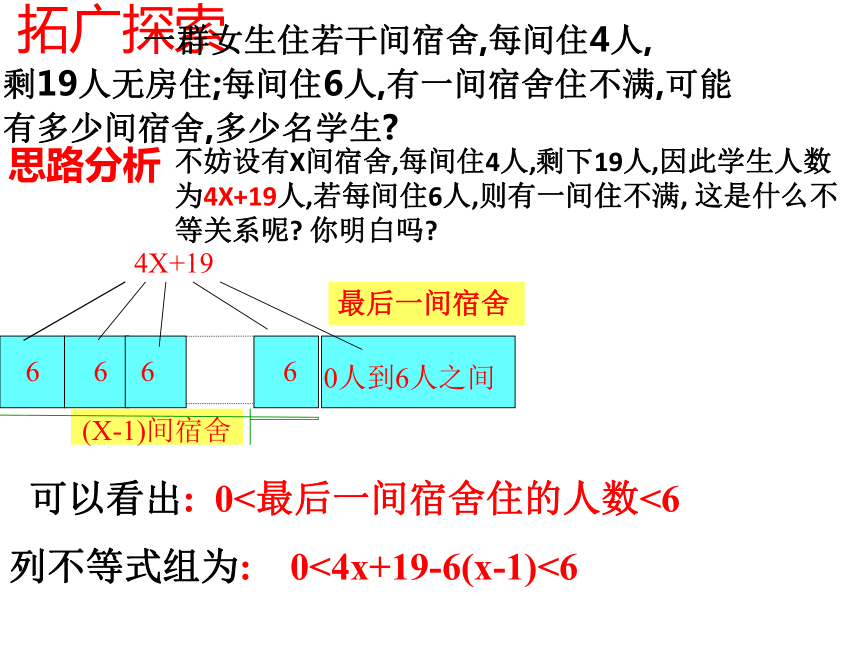
思路分析
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为:
0<4x+19-6(x-1)<6
可以看出:
0<最后一间宿舍住的人数<6
拓广探索
一群女生住若干间宿舍,每间住4人,
剩19人无房住;每间住6人,有一间宿舍住不满,可能
有多少间宿舍,多少名学生?
不妨设有X间宿舍,每间住4人,剩下19人,因此学生人数为4X+19人,若每间住6人,则有一间住不满,
这是什么不等关系呢?
你明白吗?
解:
设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.
?
一群女生住若干间宿舍,每间住4人,剩19人无房住;
每间住6人,有一间宿舍住不满,可能有多少间宿舍,
多少名学生?
拓广探索
4x+19-6(x-1)
>0
4x+19-6(x-1)
<6
即
因为x是正整数,所以x=10,11,12.
解得:
18.5实践应用,合作探索
某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案?请你设计出来.
分析(1)本题不等关系:
生产AB种产品所需的甲种原料≤360
生产AB种产品所需的乙种原料≤290
由题意,得:
9x+4(50-
x)≤360
3x+10(50-x)≤290
解:设生产A种产品x件,
则B种产品(50-x)件.
解得:
{
x≤32
x≥30
所以
30≤X≤32
可有三种生产方案:A种30件,B种20件
或A种31件,B种19件或A种32件,B种18件
对于具有多种不等关系实际的问题,可通过构建不等式组的数学模型解决,
关键是找出题中的不等关系。解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
归纳
解:设张力平均每天读x页.
由题意,得:
{
7(x+3)>98
7x<98
①
②
由不等式①得
x
>11
由不等式②得
x<
14
因此,不等式组的解集为
11
<
x<
14
因为x是正整数,所以x=12,13.
答:张力平均每天读12或13页.
练一练
一本英语书共98页,张力读了一周(7天)还没读完.
而李永不到一周就读完.李永平均每天比张力多读3页,
张力平均每天读多少页(答案取整数)?
把一些书分给几个学生,如果每人分3本,那么余8本,如果前面的每个学生分5本,那么最后一人就分不到3本.
这些书有多少本?学生有多少人?
解:
设有x名学生,则有(3x+8)本书.
由题意,得:
解得:
{
x≤6.5
x>5
所以
5<
x≤6.5
因为x是正整数,所以x=6,3x+8=26
答:
有6名学生,26本书.
0≤(3x+8)-5(x-1)<3
(3x+8)-5(x-1)≥0
(3x+8)-5(x-1)<3
即
练一练
1、把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分得2个,求学生人数和苹果数分别是多少?
练一练
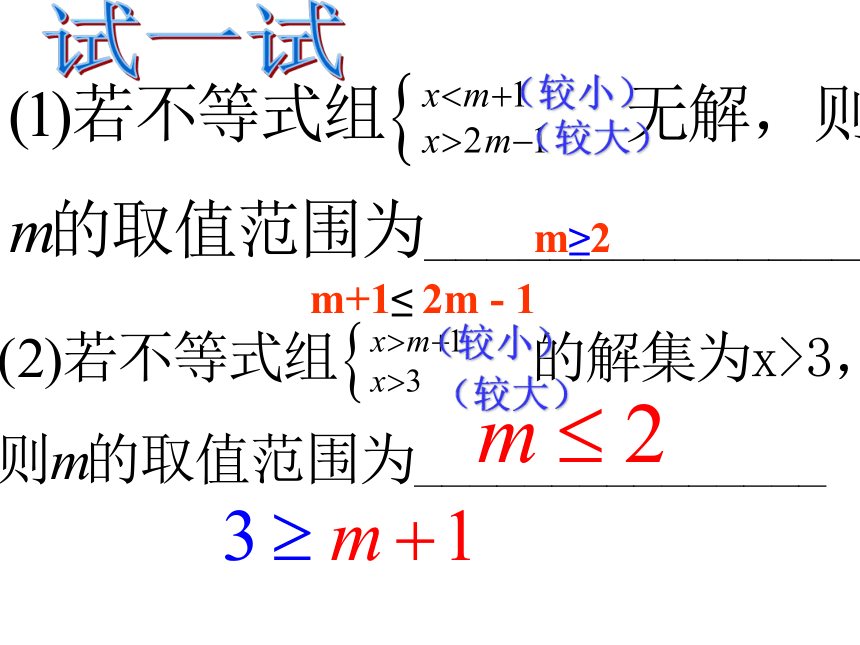
(较大)
(较小)
(较大)
(较小)
m+1≤
2m
-
1
m≥2
试一试
(3)关于x的不等式组
有解,那么m的取值范围是(
)
A、m>8
B、m≥8
C、m<8D、m≤8
C
(4)如果不等式组
的解集是x>a,则a_______b。
≥
试一试
(5)已知不等式组
的解集
为-1<x<1,则(a+1)(b-1)的值为多少?
解:由题意,得不等式组的解集是2b+32
a+1
对照-1∴a=1,b=
-
2
所以有
=1,2b+3=
-1
2
a+1
∴(a+1)(b-1)=
-
6
试一试
(6)以线段3,4,x-5为边组成三角形,
则x的取值范围是_______
6{
X-5>
1
X-5<7
(7)当方程5x-2a=5-2x的解在2和6之间时,
则a的取值范围是_________
37
9
2
2
<
a
<
(8)已知关于x的不等式组
无解,
则a的取值范围是_________
x
<
2
x
>
-1
x
>
a
a≥2
(9)已知关于x的不等式组
的整数解共有5个,求a的取值范围。
x-a≥0
3-2x>-1
通过本节课的学习谈谈你的收获?
学有所得
对于具有多种不等关系的问题,可通过不等式组解决.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
综合运用
P148
解:
设进价为x元,
由题意,得:
150-x≥10%x
150-x
≤20%x
解得:125
≤x
≤136
答:进价的范围是125元?136元.
某商品的售价是150元,商家售出
一件这种商品可获利润是进价
的10%~20%,进价的范围是什么
(精确到1元)
解:
设B型抽水机每分抽水x吨.
由题意,得:
20x
≤
1.1×30
22x≥
1.1×30
解得:1.5
≤x
≤1.65
答:
B型抽水机比A型抽水机每分多抽水0.4?0.55吨.
解:
设一次服用的剂量为x
mg.
分三次服用时,
3x≥60
3x
≤120
解得
20≤x
≤40
分四次服用时,
4x≥60
4x
≤120
解得
15≤x
≤30
答:分三次服用时,一次服用的剂量的范围为20mg?40mg.
分四次服用时,一次服用的剂量的范围为15mg?30mg.
①
②
③
解:
由①得
5x
-1>3x+3
x>2
由②
得
x-2
>
6-3x
x
>2
由③得
x
>-1
所以这三个不等式的解集是x>2
解:
原不等式组即为
3x-7≥2
3x
-7<
8
①
②
由①得
x≥3
由②
得
x<
5
所以原不等式组的解集是3
≤x<5
所以整数x=3或4
2≤3x-7<8
解:2+7≤3x<8+7
9≤3x<15
3≤x<5
2≤-3x-7<8
解:2+7≤-3x<8+7
9≤-3x<15
-3≥x>-5
-5解:去分母-9≤2x-1<15
移项
-8≤2x<16
系数化为1
-4≤x<8
解:6<-2x-1<15
7<-2x<16
-8②
①
解:由方程组得
∵x+y<0
解之得
②
①
解:解不等式①得:x<5
解不等式②得:x≥1.4
∴原不等式组的解集为1.4≤x<5
∵满足1.4≤x<5的正整数解为:2、3、4
∴原不等式组的正整数解:2、3、4
1.求下列不等式组的解集:
x>3.5
x<-1
大大取较大
小小取较小
4-12.选择题:
(1)不等式组
的解集是(
)
A.x<1
B.x
≥
2
C.
1≤
2
D.
无解
A.1
B.2
C.0
D.–1
D
C
A.x>b
B.xC.无解
D.a
C
A
①列一元一次不等式组解实际问题的一般步骤:审题——设元——列不等式(组)
——求解——检验——作答。
?
②数学建模的思想方法。
③注意:要根据实际问题的意义确定数学
模型的解。
小结
(3
)如果不等式组
无解
则m的取值范围是_______
{
2X-5≥
0
X
≤
m
m<2.5
(4)如果不等式组
的解为
-1{
X+2
>
a
X
-1
<
b
1
1
解:由题意,得不等式组的解集是a-2对照-1所以有
a-2=-1,b+1=2
所以a=1,b=1
3、已知关于x的不等式组
的整数解共有5个,求a的取值范围。
x-a≥0
3-2x>-1
第九章
不等式与不等式组
9.3
一元一次不等
式组(2)
设a、b是已知有理数且a>b,那么不等式组的解集怎么确定.
不等式组
数轴表示
解集(即公共部分)
b
a
b
a
b
a
b
a
无解
X>a
b
10天的产品数量
500;
“提前完成任务”的意思是:提高速度后,10天
的产品的数量
500.
3个小组计划在10
天内生产500件产品(每天生产量相同),按原计划的生产速度,不能完成生产任务;如果每个小组比原先多生产1件产品,就能提前完成任务。每个小组原先每天生产多少件?
典例探究
小于
大于
你能找出不等关系吗?
你能列出不等式组了吗?
解:设每个小组原先每天生产X件产品
,则提高速度后每天生产(X+1)
件产品
。根据题中前后两个条件,
得
3?×
10X
<
500
3
×10(X+1)>
500
(1)
(2)
根据题意,
X的值应是整数,所以X=16
答:每个小组原先每天生产16件产品。
解得:15
<
X
<16
思路分析
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为:
0<4x+19-6(x-1)<6
可以看出:
0<最后一间宿舍住的人数<6
拓广探索
一群女生住若干间宿舍,每间住4人,
剩19人无房住;每间住6人,有一间宿舍住不满,可能
有多少间宿舍,多少名学生?
不妨设有X间宿舍,每间住4人,剩下19人,因此学生人数为4X+19人,若每间住6人,则有一间住不满,
这是什么不等关系呢?
你明白吗?
解:
设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.
?
一群女生住若干间宿舍,每间住4人,剩19人无房住;
每间住6人,有一间宿舍住不满,可能有多少间宿舍,
多少名学生?
拓广探索
4x+19-6(x-1)
>0
4x+19-6(x-1)
<6
即
因为x是正整数,所以x=10,11,12.
解得:
18.5
某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,有哪几种符合的生产方案?请你设计出来.
分析(1)本题不等关系:
生产AB种产品所需的甲种原料≤360
生产AB种产品所需的乙种原料≤290
由题意,得:
9x+4(50-
x)≤360
3x+10(50-x)≤290
解:设生产A种产品x件,
则B种产品(50-x)件.
解得:
{
x≤32
x≥30
所以
30≤X≤32
可有三种生产方案:A种30件,B种20件
或A种31件,B种19件或A种32件,B种18件
对于具有多种不等关系实际的问题,可通过构建不等式组的数学模型解决,
关键是找出题中的不等关系。解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
归纳
解:设张力平均每天读x页.
由题意,得:
{
7(x+3)>98
7x<98
①
②
由不等式①得
x
>11
由不等式②得
x<
14
因此,不等式组的解集为
11
<
x<
14
因为x是正整数,所以x=12,13.
答:张力平均每天读12或13页.
练一练
一本英语书共98页,张力读了一周(7天)还没读完.
而李永不到一周就读完.李永平均每天比张力多读3页,
张力平均每天读多少页(答案取整数)?
把一些书分给几个学生,如果每人分3本,那么余8本,如果前面的每个学生分5本,那么最后一人就分不到3本.
这些书有多少本?学生有多少人?
解:
设有x名学生,则有(3x+8)本书.
由题意,得:
解得:
{
x≤6.5
x>5
所以
5<
x≤6.5
因为x是正整数,所以x=6,3x+8=26
答:
有6名学生,26本书.
0≤(3x+8)-5(x-1)<3
(3x+8)-5(x-1)≥0
(3x+8)-5(x-1)<3
即
练一练
1、把一篮苹果分给几个学生,若每人分4个,则剩余3个;若每人分6个,则最后一个学生最多分得2个,求学生人数和苹果数分别是多少?
练一练
(较大)
(较小)
(较大)
(较小)
m+1≤
2m
-
1
m≥2
试一试
(3)关于x的不等式组
有解,那么m的取值范围是(
)
A、m>8
B、m≥8
C、m<8D、m≤8
C
(4)如果不等式组
的解集是x>a,则a_______b。
≥
试一试
(5)已知不等式组
的解集
为-1<x<1,则(a+1)(b-1)的值为多少?
解:由题意,得不等式组的解集是2b+3
a+1
对照-1
-
2
所以有
=1,2b+3=
-1
2
a+1
∴(a+1)(b-1)=
-
6
试一试
(6)以线段3,4,x-5为边组成三角形,
则x的取值范围是_______
6
X-5>
1
X-5<7
(7)当方程5x-2a=5-2x的解在2和6之间时,
则a的取值范围是_________
37
9
2
2
<
a
<
(8)已知关于x的不等式组
无解,
则a的取值范围是_________
x
<
2
x
>
-1
x
>
a
a≥2
(9)已知关于x的不等式组
的整数解共有5个,求a的取值范围。
x-a≥0
3-2x>-1
通过本节课的学习谈谈你的收获?
学有所得
对于具有多种不等关系的问题,可通过不等式组解决.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.
综合运用
P148
解:
设进价为x元,
由题意,得:
150-x≥10%x
150-x
≤20%x
解得:125
≤x
≤136
答:进价的范围是125元?136元.
某商品的售价是150元,商家售出
一件这种商品可获利润是进价
的10%~20%,进价的范围是什么
(精确到1元)
解:
设B型抽水机每分抽水x吨.
由题意,得:
20x
≤
1.1×30
22x≥
1.1×30
解得:1.5
≤x
≤1.65
答:
B型抽水机比A型抽水机每分多抽水0.4?0.55吨.
解:
设一次服用的剂量为x
mg.
分三次服用时,
3x≥60
3x
≤120
解得
20≤x
≤40
分四次服用时,
4x≥60
4x
≤120
解得
15≤x
≤30
答:分三次服用时,一次服用的剂量的范围为20mg?40mg.
分四次服用时,一次服用的剂量的范围为15mg?30mg.
①
②
③
解:
由①得
5x
-1>3x+3
x>2
由②
得
x-2
>
6-3x
x
>2
由③得
x
>-1
所以这三个不等式的解集是x>2
解:
原不等式组即为
3x-7≥2
3x
-7<
8
①
②
由①得
x≥3
由②
得
x<
5
所以原不等式组的解集是3
≤x<5
所以整数x=3或4
2≤3x-7<8
解:2+7≤3x<8+7
9≤3x<15
3≤x<5
2≤-3x-7<8
解:2+7≤-3x<8+7
9≤-3x<15
-3≥x>-5
-5
移项
-8≤2x<16
系数化为1
-4≤x<8
解:6<-2x-1<15
7<-2x<16
-8
①
解:由方程组得
∵x+y<0
解之得
②
①
解:解不等式①得:x<5
解不等式②得:x≥1.4
∴原不等式组的解集为1.4≤x<5
∵满足1.4≤x<5的正整数解为:2、3、4
∴原不等式组的正整数解:2、3、4
1.求下列不等式组的解集:
x>3.5
x<-1
大大取较大
小小取较小
4
(1)不等式组
的解集是(
)
A.x<1
B.x
≥
2
C.
1
2
D.
无解
A.1
B.2
C.0
D.–1
D
C
A.x>b
B.x
D.a
A
①列一元一次不等式组解实际问题的一般步骤:审题——设元——列不等式(组)
——求解——检验——作答。
?
②数学建模的思想方法。
③注意:要根据实际问题的意义确定数学
模型的解。
小结
(3
)如果不等式组
无解
则m的取值范围是_______
{
2X-5≥
0
X
≤
m
m<2.5
(4)如果不等式组
的解为
-1
X+2
>
a
X
-1
<
b
1
1
解:由题意,得不等式组的解集是a-2
a-2=-1,b+1=2
所以a=1,b=1
3、已知关于x的不等式组
的整数解共有5个,求a的取值范围。
x-a≥0
3-2x>-1
