(新人教版)六年级数学下册课件 比例的基本性质
文档属性
| 名称 | (新人教版)六年级数学下册课件 比例的基本性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 637.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-03 16:11:44 | ||
图片预览




文档简介
(共22张PPT)
数
学
比例的基本性质
高集乡一初中 高光林
2012年2月
温故知新:
1、什么叫做比例?
2、什么叫做比?比各项的名称叫什么?比的基本性质是什么?
表示两个比相等的式子叫做比例。
两个比相等可以理解为两个比的比值相等。
比例是个式子,表示两个比相等的关系。
两个数相除又叫做两个数的比。
比的前项和后项同时乖以(或除以)一个相同的数(O除外),比值不变,这就是比的基本性质。
3 :4=
前项
后项
比值
自学提示:
1、比例各部分名称是什么?
2、算一算例题中两个内项之积和两个外项之积,你有什么发现?
3、把比例改写成分数形式,分子和分母分别交叉相乖,所得的积又有什么关系?
4、通过上面两个问题,你能总结出比例的基本性质吗?
5、根据比例的基本性质,怎样判断两个比是否能组成比例?
温馨提示:同学们认真看课本P34页内容,思考自学提示中的问题。自己动手算一算,再在小组中讨论以上问题!
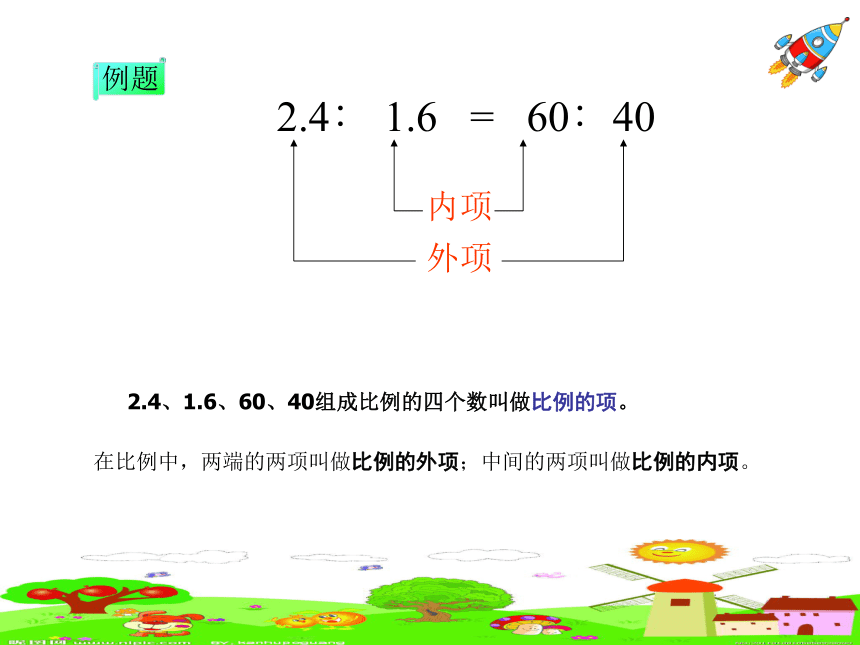
例题
2.4∶ 1.6 = 60∶40
外项
内项
2.4、1.6、60、40组成比例的四个数叫做比例的项。
在比例中,两端的两项叫做比例的外项;中间的两项叫做比例的内项。
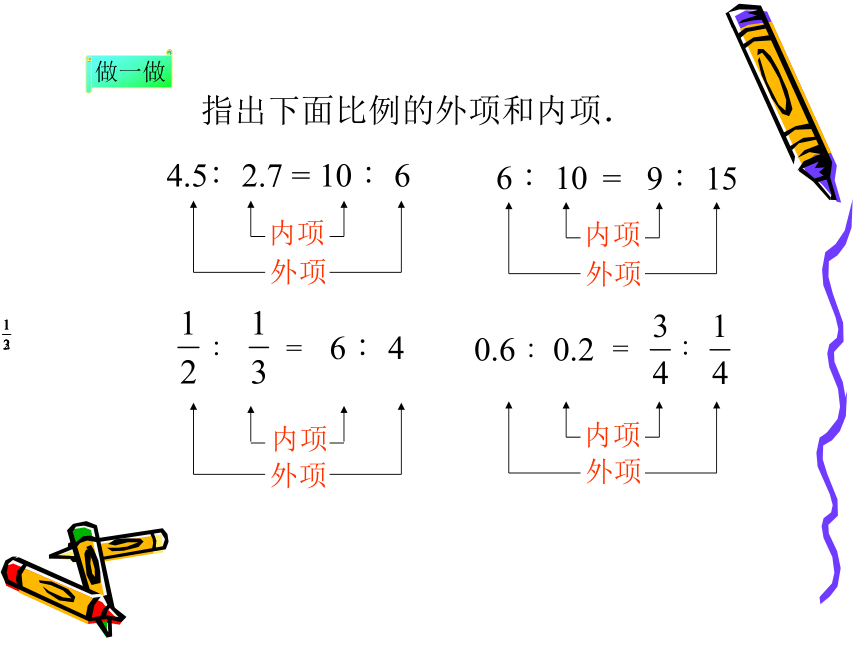
指出下面比例的外项和内项.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
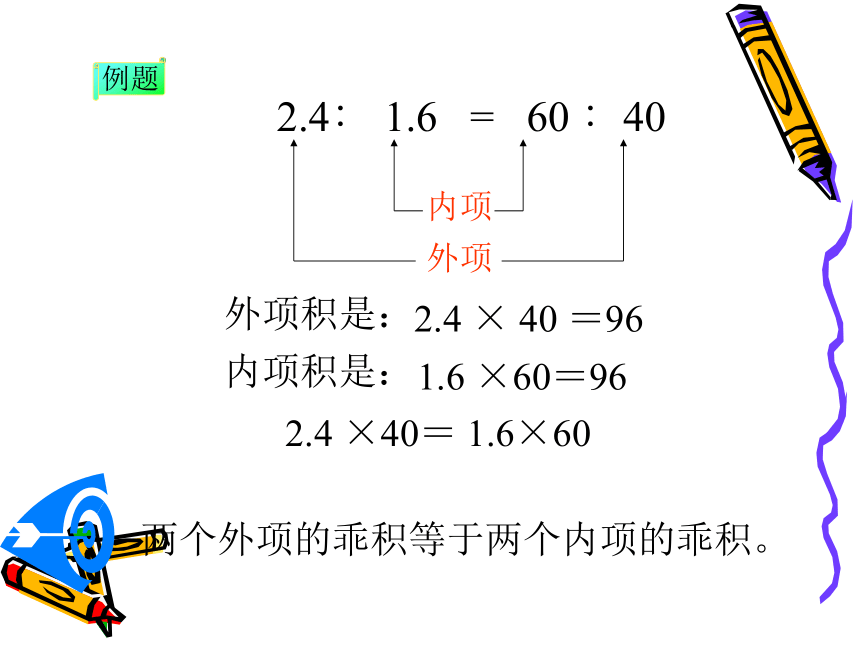
例题
2.4∶ 1.6 = 60 ∶40
外项
内项
内项积是:
1.6 ×60=96
外项积是:
2.4 × 40 =96
2.4 ×40= 1.6×60
两个外项的乖积等于两个内项的乖积。
计算下面比例的外项积和内项积.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
0.6 ∶0.2
∶
=
4.5 × 6 = 27
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
2.7 × 10 = 27
6 × 15 = 90
10 × 9 = 90
× 4 = 2
× 6 = 2
0.6 ×
= 0.15
0.2 ×
= 0.15
把比例改成分数形式后,我们再来观察:
2.4:1.6=60:40
2.4×40=1.6×60
把比例改成分数形式后,等号两边的分子和分母交叉相乖所得的积相等。
96
96
=
规律总结:
2.4 ∶1.6= 60 ∶40
外项
内项
内项积是:
1.6× 60=96
外项积是:
2.4 ×40 = 96
2.4× 40= 1.6 ×60
在比例里,两个外项的积等于两个内项的积.
这叫做比例的基本性质.
例题:
应用比例的基本性质,判断下面哪组中的两个比
可以组成比例.
6∶3 和 8∶5
0.2∶2.5 和 4∶50
因为: 6 × 5 = 30
3 × 8 = 24
所以: 6∶3 和 8∶5
不能组成比例.
因为: 0.2 × 50 = 10
2.5 × 4 = 10
所以:0.2∶2.5 = 4∶50
30
24
≠
10 = 10
根据比例的基本性质,两个比如果内项之积等于外项之积,那么这两个比就能组成比例;否则,不能组成比例。
牛刀小试:
应用比例的意义或者基本性质,判断下面
的两个比是否可以组成比例.
6∶9 和 9∶12
所以: 1.25∶5 和 2∶8
能组成比例.
因为: 6 × 12 = 72
9 × 9 = 81
因为: 1.25 × 8=10
比例的基本性质:
所以: 6∶9 和 9∶12
不能组成比例.
72 ≠ 81
1.25:5和2:8
比例的基本性质:
10=10
5×2=10
做一做
应用比例的意义或者基本性质,判断下面哪组中
的两个比可以组成比例.
1.4∶2 和 7∶10
因为: 1.4 ∶ 2 =0.7
所以: 1.4∶2 和 7∶10
可以组成比例.
因为: 1.4 × 10 = 14
2 × 7 = 14
比例的意义:
7∶10 = 0.7
比例的基本性质:
0.7 = 0.7
14 = 14
所以: 1.4∶2 和 7∶10
可以组成比例.
做一做
应用比例的意义或者基本性质,判断下面
的两个比是否可以组成比例.
因为: 0.5 ∶ 0.2 =2.5
比例的意义:
比例的基本性质:
2.5 = 2.5
0.125 = 0.125
0.5∶0.2 和
∶
∶
= 2.5
因为: 0.5 ×
= 0.125
0.2 ×
= 0.125
所以: 0.5∶0.2 和
∶
可以组成比例.
所以: 0.5∶0.2 和
∶
可以组成比例.
学了本节,你有什么收获?
我会:
我知:
比例各部分的名称是什么。
比例的基本性质。
怎样判断两个比是否组成比例。两种方法:一是根据比例的意义;二是根据比例的基本性质。
做一做
应用比例的意义或者基本性质,判断下面哪组中
的两个比可以组成比例.
比例的意义:
比例的基本性质:
7.5 = 7.5
所以: 0.5∶0.2 和
∶
可以组成比例.
所以: 0.5∶0.2 和
∶
可以组成比例.
∶
和 7.5∶1
因为:
∶
= 7.5
7.5∶1 = 7.5
因为:
× 1 =
× 0.75 =
=
思考
下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个).
2、3、4 和 6
因为 2 × 6 = 3 × 4 所以这四个数可以组成比例
2 ∶3 = 4 ∶6
2 ∶4 = 3 ∶6
6 ∶4 = 3 ∶2
6 ∶3 = 4 ∶2
4 ∶2 = 6 ∶3
4 ∶6 = 2 ∶3
3 ∶6 = 2 ∶4
3 ∶2 = 6 ∶4
欢迎指导!再见!
数
学
比例的基本性质
高集乡一初中 高光林
2012年2月
温故知新:
1、什么叫做比例?
2、什么叫做比?比各项的名称叫什么?比的基本性质是什么?
表示两个比相等的式子叫做比例。
两个比相等可以理解为两个比的比值相等。
比例是个式子,表示两个比相等的关系。
两个数相除又叫做两个数的比。
比的前项和后项同时乖以(或除以)一个相同的数(O除外),比值不变,这就是比的基本性质。
3 :4=
前项
后项
比值
自学提示:
1、比例各部分名称是什么?
2、算一算例题中两个内项之积和两个外项之积,你有什么发现?
3、把比例改写成分数形式,分子和分母分别交叉相乖,所得的积又有什么关系?
4、通过上面两个问题,你能总结出比例的基本性质吗?
5、根据比例的基本性质,怎样判断两个比是否能组成比例?
温馨提示:同学们认真看课本P34页内容,思考自学提示中的问题。自己动手算一算,再在小组中讨论以上问题!
例题
2.4∶ 1.6 = 60∶40
外项
内项
2.4、1.6、60、40组成比例的四个数叫做比例的项。
在比例中,两端的两项叫做比例的外项;中间的两项叫做比例的内项。
指出下面比例的外项和内项.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
0.6 ∶0.2
∶
=
外项
外项
内项
内项
外项
内项
外项
内项
例题
2.4∶ 1.6 = 60 ∶40
外项
内项
内项积是:
1.6 ×60=96
外项积是:
2.4 × 40 =96
2.4 ×40= 1.6×60
两个外项的乖积等于两个内项的乖积。
计算下面比例的外项积和内项积.
4.5∶2.7 = 10 ∶6
6 ∶10
= 9 ∶15
做一做
∶
=
6 ∶4
0.6 ∶0.2
∶
=
4.5 × 6 = 27
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
外项积:
内项积:
2.7 × 10 = 27
6 × 15 = 90
10 × 9 = 90
× 4 = 2
× 6 = 2
0.6 ×
= 0.15
0.2 ×
= 0.15
把比例改成分数形式后,我们再来观察:
2.4:1.6=60:40
2.4×40=1.6×60
把比例改成分数形式后,等号两边的分子和分母交叉相乖所得的积相等。
96
96
=
规律总结:
2.4 ∶1.6= 60 ∶40
外项
内项
内项积是:
1.6× 60=96
外项积是:
2.4 ×40 = 96
2.4× 40= 1.6 ×60
在比例里,两个外项的积等于两个内项的积.
这叫做比例的基本性质.
例题:
应用比例的基本性质,判断下面哪组中的两个比
可以组成比例.
6∶3 和 8∶5
0.2∶2.5 和 4∶50
因为: 6 × 5 = 30
3 × 8 = 24
所以: 6∶3 和 8∶5
不能组成比例.
因为: 0.2 × 50 = 10
2.5 × 4 = 10
所以:0.2∶2.5 = 4∶50
30
24
≠
10 = 10
根据比例的基本性质,两个比如果内项之积等于外项之积,那么这两个比就能组成比例;否则,不能组成比例。
牛刀小试:
应用比例的意义或者基本性质,判断下面
的两个比是否可以组成比例.
6∶9 和 9∶12
所以: 1.25∶5 和 2∶8
能组成比例.
因为: 6 × 12 = 72
9 × 9 = 81
因为: 1.25 × 8=10
比例的基本性质:
所以: 6∶9 和 9∶12
不能组成比例.
72 ≠ 81
1.25:5和2:8
比例的基本性质:
10=10
5×2=10
做一做
应用比例的意义或者基本性质,判断下面哪组中
的两个比可以组成比例.
1.4∶2 和 7∶10
因为: 1.4 ∶ 2 =0.7
所以: 1.4∶2 和 7∶10
可以组成比例.
因为: 1.4 × 10 = 14
2 × 7 = 14
比例的意义:
7∶10 = 0.7
比例的基本性质:
0.7 = 0.7
14 = 14
所以: 1.4∶2 和 7∶10
可以组成比例.
做一做
应用比例的意义或者基本性质,判断下面
的两个比是否可以组成比例.
因为: 0.5 ∶ 0.2 =2.5
比例的意义:
比例的基本性质:
2.5 = 2.5
0.125 = 0.125
0.5∶0.2 和
∶
∶
= 2.5
因为: 0.5 ×
= 0.125
0.2 ×
= 0.125
所以: 0.5∶0.2 和
∶
可以组成比例.
所以: 0.5∶0.2 和
∶
可以组成比例.
学了本节,你有什么收获?
我会:
我知:
比例各部分的名称是什么。
比例的基本性质。
怎样判断两个比是否组成比例。两种方法:一是根据比例的意义;二是根据比例的基本性质。
做一做
应用比例的意义或者基本性质,判断下面哪组中
的两个比可以组成比例.
比例的意义:
比例的基本性质:
7.5 = 7.5
所以: 0.5∶0.2 和
∶
可以组成比例.
所以: 0.5∶0.2 和
∶
可以组成比例.
∶
和 7.5∶1
因为:
∶
= 7.5
7.5∶1 = 7.5
因为:
× 1 =
× 0.75 =
=
思考
下面的四个数可以组成比例吗?把组成的比例
写出来(能写几个写几个).
2、3、4 和 6
因为 2 × 6 = 3 × 4 所以这四个数可以组成比例
2 ∶3 = 4 ∶6
2 ∶4 = 3 ∶6
6 ∶4 = 3 ∶2
6 ∶3 = 4 ∶2
4 ∶2 = 6 ∶3
4 ∶6 = 2 ∶3
3 ∶6 = 2 ∶4
3 ∶2 = 6 ∶4
欢迎指导!再见!
