2020-2021学年人教版数学八年级下册18.2:特殊的平行四边形 专项练习(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册18.2:特殊的平行四边形 专项练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 854.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 11:30:30 | ||
图片预览

文档简介
18.2特殊的平行四边形专项练习
一、单选题
1.下列说法中,错误的是(
)
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的平行四边形是菱形
C.对角线相等且互相垂直的四边形是正方形
D.对角线相等且互相平分的四边形是矩形
2.正方形?菱形?矩形都具有的性质是(
)
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角线平分一组对角
3.平行四边形的对角线和交于点,添加一个条件不能使平行四边形变为矩形的是(
)
A.
B.
C.
D.
4.如图,在菱形中,点是的中点,点是的中点,连接,如果,那么菱形的周长为( )
A.4
B.8
C.16
D.32
5.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A(﹣3,0),B(2,b),则b的值为( )
A.3
B.2
C.﹣3
D.﹣2
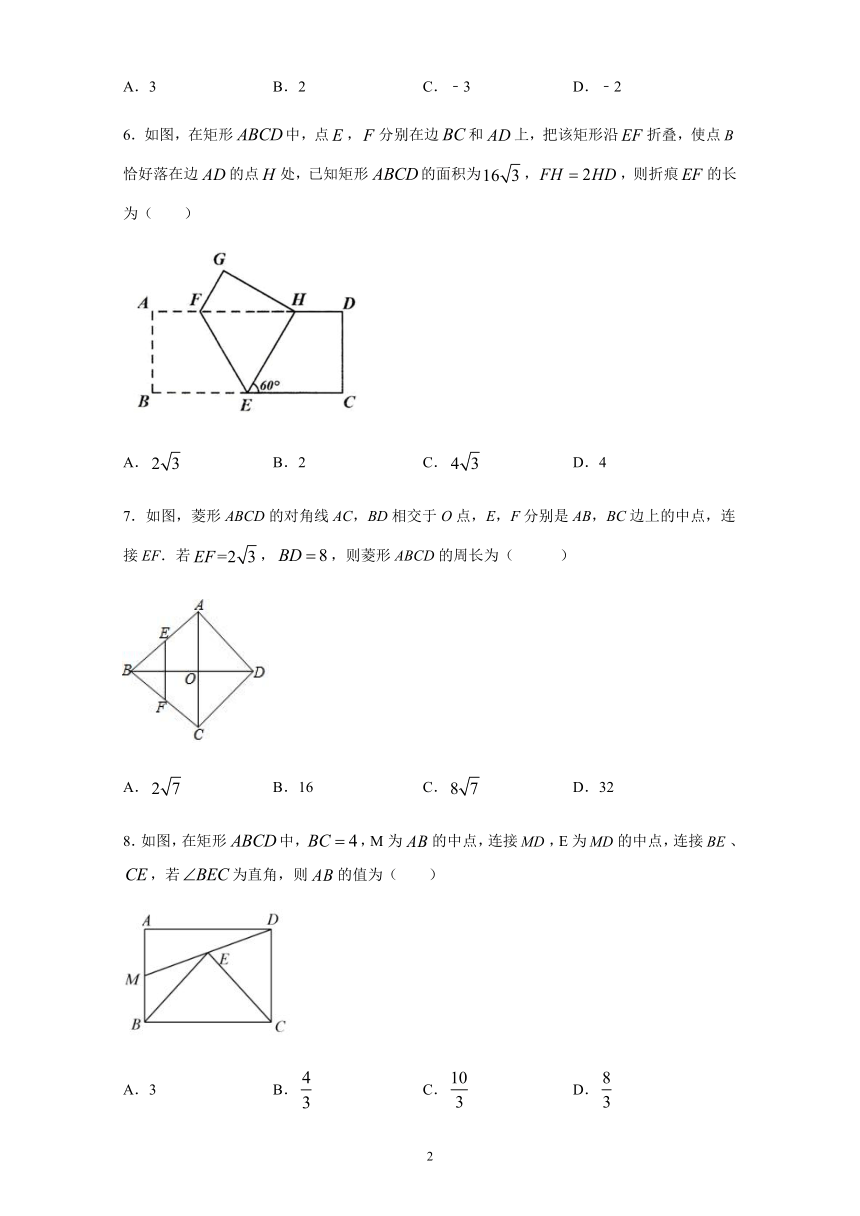
6.如图,在矩形中,点,分别在边和上,把该矩形沿折叠,使点恰好落在边的点处,已知矩形的面积为,,则折痕的长为(
)
A.
B.2
C.
D.4
7.如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若,,则菱形ABCD的周长为( )
A.
B.16
C.
D.32
8.如图,在矩形中,,M为的中点,连接,E为的中点,连接、,若为直角,则的值为(
)
A.3
B.
C.
D.
9.如图,在菱形中,,E、F分别是边、的中点,于点P,则的度数是(
).
A.50°
B.45°
C.40°
D.30°
10.如图,在正方形ABCD中,E、F分别是BC、CD上的点,若△AEF是边长为2的等边三角形,则正方形的边长是( )
A.
B.+1
C.
D.
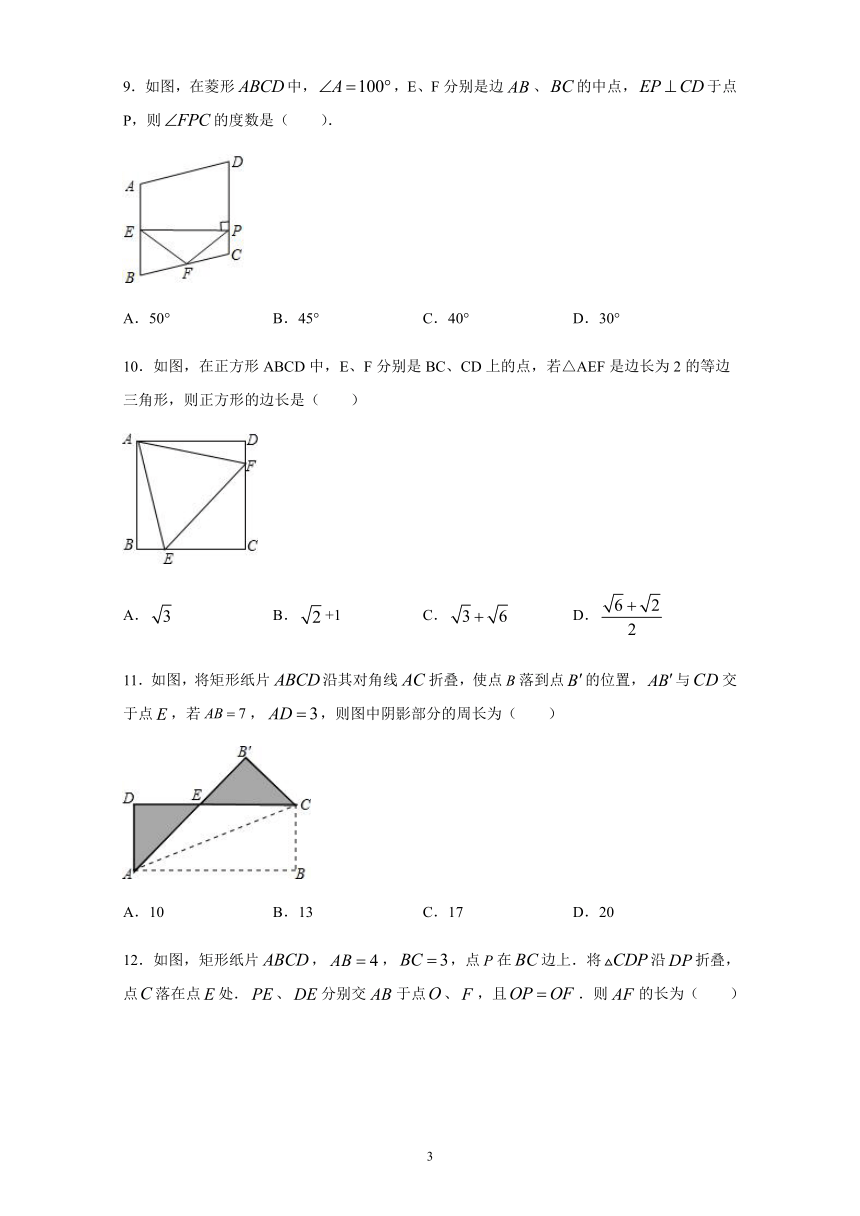
11.如图,将矩形纸片沿其对角线折叠,使点落到点的位置,与交于点,若,,则图中阴影部分的周长为(
)
A.10
B.13
C.17
D.20
12.如图,矩形纸片,,,点在边上.将沿折叠,点落在点处.、分别交于点、,且.则的长为(
)
A.2
B.
C.
D.
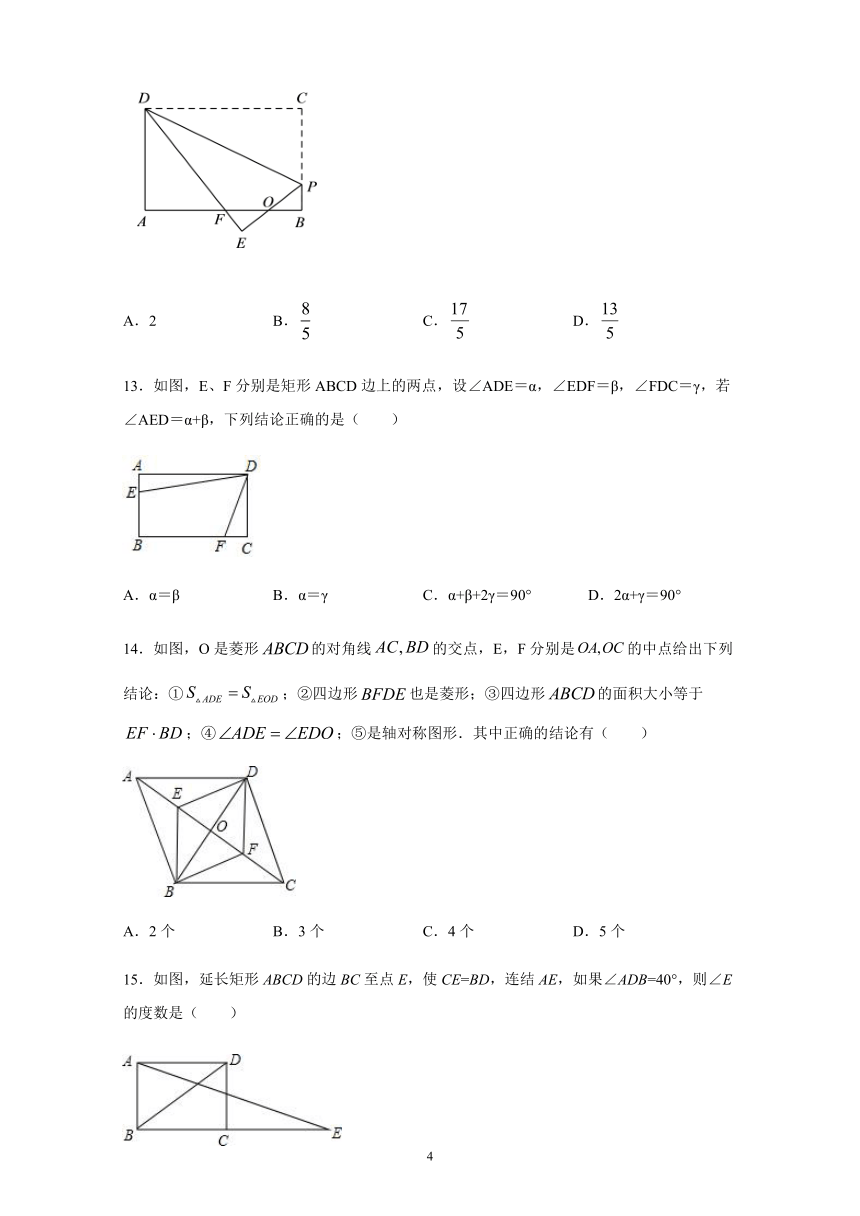
13.如图,E、F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是(
)
A.α=β
B.α=γ
C.α+β+2γ=90°
D.2α+γ=90°
14.如图,O是菱形的对角线的交点,E,F分别是的中点给出下列结论:①;②四边形也是菱形;③四边形的面积大小等于;④;⑤是轴对称图形.其中正确的结论有(
)
A.2个
B.3个
C.4个
D.5个
15.如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=40°,则∠E的度数是(
)
A.10°
B.20°
C.30°
D.40°
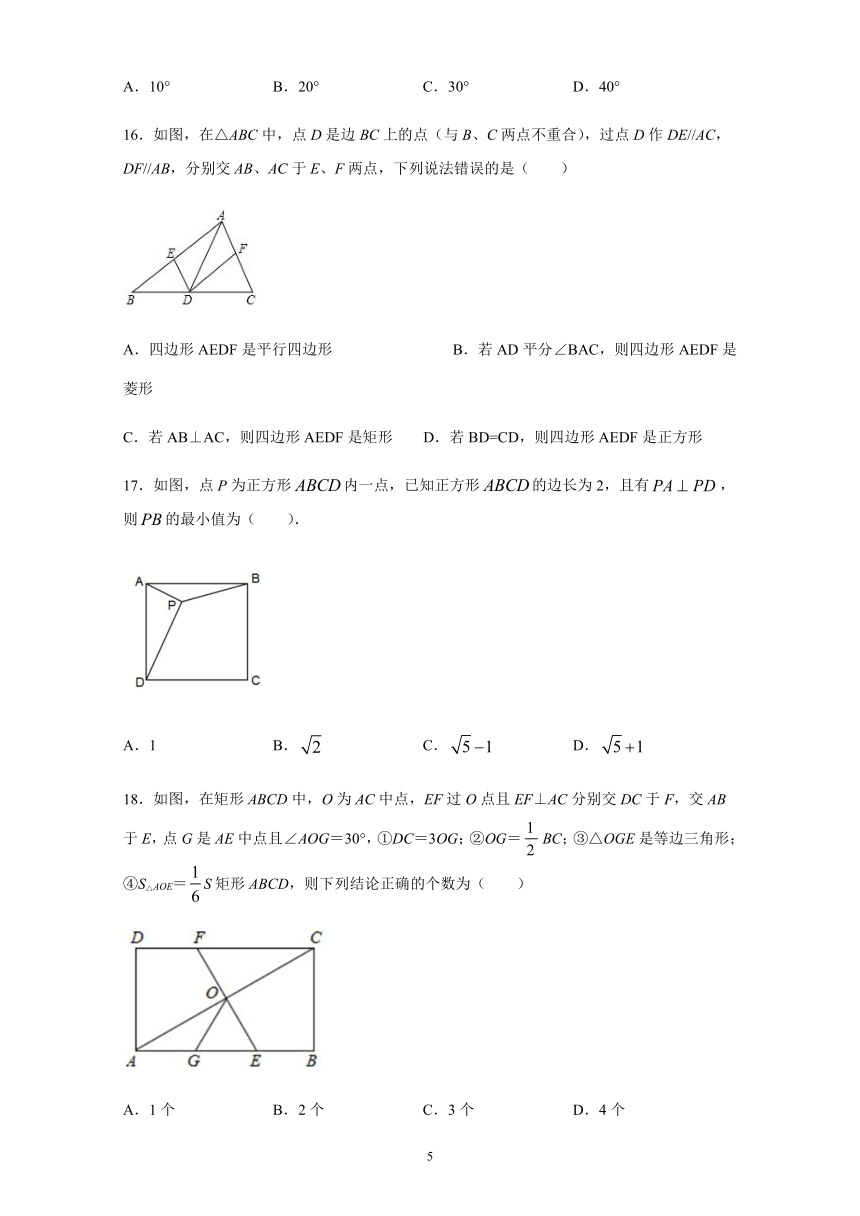
16.如图,在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE//AC,DF//AB,分别交AB、AC于E、F两点,下列说法错误的是(
)
A.四边形AEDF是平行四边形
B.若AD平分∠BAC,则四边形AEDF是菱形
C.若AB⊥AC,则四边形AEDF是矩形
D.若BD=CD,则四边形AEDF是正方形
17.如图,点P为正方形内一点,已知正方形的边长为2,且有,则的最小值为(
).
A.1
B.
C.
D.
18.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,①DC=3OG;②OG=BC;③△OGE是等边三角形;④S△AOE=S矩形ABCD,则下列结论正确的个数为( )
A.1个
B.2个
C.3个
D.4个
19.如图,在中,,以的各边为边分别作正方形,正方形与正方形.延长,分别交,于点,,连结,.图中两块阴影部分面积分别记为,,若,四边形,则四边形的面积为(
)
A.5
B.6
C.8
D.9
20.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)所示).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成的记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若EF=4,则S1+S2+S3的值是( )
A.32
B.38
C.48
D.80
二、填空题
21.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为__________.
22.如图,ABCD为正方形,O为AC、BD的交点,△DCE为直角三角形,∠CED=90°,∠DCE=30°,若正方形的边长为2,则OE的长为__________.
23.如图,ABCD是一张长方形纸片,且AD=2AB=8,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′)折痕交于点G,则BG=______.
24.如图,点为正方形的边的延长线上一点,以为边在的另一侧作正方形,连接,若,,则的面积为______.
25.对于任意三角形,如果存在一个菱形,使得这个菱形的一条边与三角形的一条边重合,且三角形的这条边所对的顶点在菱形的这条边的对边上,那么称这个菱形为该三角形的“最优覆盖菱形”.问题:如图,在中,,,且的面积为m,如果存在“最优覆盖菱形”为菱形,那么m的取值范围是________.
三、解答题
26.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.
(1)求证:EF=AE+CF
(2)当AE=1时,求EF的长.
27.如图,已知平行四边形ABCD,若M,N是BD上两点,且BM=DN,AC=2OM,
(1)求证:四边形
AMCN
是矩形;
(2)△ABC
满足什么条件,四边形AMCN是正方形,请说明理由.
28.已知:如图,在菱形中,E,F分别在边,上,且,求证:.
29.如图,在四边形ABCD中,AD∥BC,AB=BC,BD平分∠ABC.过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若CE=,四边形ABCD的面积为4,求DE的长.
30.如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
31.如图,将平行四边形ABCD折叠,使点C与点A重合,折痕EF交BC于E交AD于F,交AC于G,连接AE,CF.
(1)求证:四边形AECF为菱形;
(2)若四边形AECF恰为正方形,且AB=5,BC=7,求平行四边形ABCD的面积.
(
2
)
(
1
)
参考答案
1.C
解:A.对角线互相平分的四边形是平行四边形,此说法正确,不符合题意;
B.对角线互相垂直的平行四边形是菱形,此说法正确,不符合题意;
C.对角线相等且互相垂直的平行四边形是正方形,故原说法错误,符合题意;
D.对角线相等且互相平分的四边形是矩形,此说法正确,不符合题意.
2.B
解:∵正方形的对角线互相平分,互相垂直,相等且平分一组对角,
菱形的对角线互相平分,互相垂直且平分一组对角,
矩形的对角线互相平分且相等,
∴正方形、菱形、矩形都具有的性质是:对角线互相平分.
3.D
解:∵四边形是平行四边形,
∴,,
A.
时,,
∴平行四边形是矩形,故选项A不符合题意;
B.四边形是平行四边形,,
∴平行四边形是矩形,故选项B不符合题意;
C.∵,
∴,
∴,
∴平行四边形是矩形,故选项C不符合题意;
D.四边形是平行四边形,,
∴平行四边形是菱形,故选项D符合题意;
4.D
解:∵E为AB中点,F为AC中点,
∴线段EF为的中位线,
∴.
∵四边形ABCD为菱形,
∴该菱形的周长=4×8=32.
5.C
解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴BM=OA,
∵A(,0),B(2,b),
∴BM=OA=3,
∴b=.
6.D
解:
由折叠的性质可知,BE=EH,AF=FG,GH=AB,∠BEF=∠HEF,
∵∠BEF+∠HEF=180°-∠HEC=120°,
∴∠HEF=60°
∵FH∥CE,∠HEC=60°,
∴∠FHE=∠HEC=60°,
∴△HEF为等边三角形,
∴EF=HE=FH,
∵∠FHE=60°,∠B=∠GHE=∠FHE+∠GHF=90°,
∴∠GHF=30°,
在Rt△FGH中,∠GHF=30°,
∴FH=2FG=2AF,
∴设FG=x,则FH=2x,HD=x,
则有,
∴AD=AF+FH+HD=4x,
又∵矩形ABCD的面积为,
∴,
∴x=2或x=-2(舍),
∴EF=FH=4,
7.C
解:∵E,F分别是AB,BC边上的中点,EF=,
∴AC=2EF=,
∵四边形ABCD是菱形,,
∴AC⊥BD,OA=AC=,OB=BD=4,
∴AB==,
∴菱形ABCD的周长为:=.
8.D
解:连接AE,过点E作EF⊥AD,并延长,交BC于点H,如图所示:
∵四边形是矩形,,
∴,,,,
∴,
∴四边形是矩形,
∵E为的中点,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵M为的中点,
∴,
∴,
∴,
∴;
9.A
解:延长PF交AB的延长线于点G.如图所示:
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠GBF=∠PCF,
∵F是边BC的中点,
∴BF=CF,
在△BGF与△CPF中,
∴△BGF≌△CPF(ASA)
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEP=90°,
∴EF=PG,
∵PF=PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP-∠FEP=∠EPC-∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=80°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=
(180°-80°)=50°,
∴∠FPC=50°;
10.D
解:由题知:△AEF是边长为2的等边三角形,
∴∠EAF=60°,AE=AF,∴∠BAE+∠DAF=30°,
又AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF=15°,
如图,作∠AEH=∠BAE=15°,交AB于H,
∴∠BHE=30°,AH=HE,∴HE=2BE=AH,BH=BE,∴AB=(2+)BE,
∵AE2=BE2+AB2,
∴4=BE2+(2+)2×BE2,
∴BE=(﹣1)=,
∴AB=(2+)BE=,
11.D
解:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°,
∵∠B′EC=∠DEA,
在△AED和△CEB′中,
,
∴△AED≌△CEB′(AAS);
∴EA=EC,
∴阴影部分的周长为AD+DE+EA+EB′+B′C+EC
=AD+DE+EC+EA+EB′+B′C
=AD+DC+AB′+B′C
=3+7+7+3
=20,
12.B
解:∵四边形ABCD是矩形
∴,,
根据折叠的性质,得:,,
在与中
∴
∴,
∴
设,则
∴
∴
在中,由勾股定理得:
解得:
即
13.B
解:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵∠ADE=α,∠EDF=β,∠FDC=γ,
∴α+β+γ=90°,
∵∠AED+α=90°,∠AED=α+β,
∴2α+β=90°,
∴α+β+γ=2α+β,
∴α=γ,
14.C
解:①正确
∵E、F分别是OA、OC的中点.
∴AE=OE.
∵S△ADEAE×ODOE×OD=S△EOD
∴S△ADE=S△EOD.
②正确
∵四边形ABCD是菱形,E,F分别是OA,OC的中点.
∴EF⊥OD,OE=OF.
∵OD=OB.
∴四边形BFDE是菱形.
③正确
∵菱形ABCD的面积AC×BD.
∵E、F分别是OA、OC的中点.
∴EFAC.
∴菱形ABCD的面积=EF×BD.
④不正确
由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.
⑤正确
∵EF⊥OD,OE=OF,OD=OD.
∴△DEO≌△DFO.
∴△DEF是轴对称图形.
∴正确的结论有四个,分别是①②③⑤,
15.B
解:连接AC,交BD于点O,
∵四边形ABCD是矩形,
∴AC=BD,
∵EC=BD,
∴AC=CE,
∴∠E=∠CAE,
∵OB=OC,
∴∠ACB=∠DBC,
又∵AD∥BC,
∴∠DBC=∠ADB,
∴∠ACB=∠ADB=40°,
∵∠ACB=∠E+∠CAE,
∴∠E=∠CAE=20°,
16.D
解:∵DE//AC,DF//AB,
∴四边形AEDF是平行四边形,故选项A正确,不符合题意;
若AD平分∠BAC,则∠EAD=∠FAD,
又∵∠EAD=∠FDA,
∴∠FAD=∠FDA
,∴FA=FD,
∴平行四边形AEDF是菱形,
故选项B正确,不符合题意;
∵AB⊥AC,
∴平行四边形AEDF是矩形,
故选项C正确,不符合题意;
若BD=CD,则四边形AEDF不一定是正方形;选项D错误,符合题意.
17.C
解:取AD中点E,连接PE、BE,
∵正方形的边长为2,
∴PE=AE=1,
,
∵,
当P、E、B三点共线时,最小,最小值为,
18.C
解:,点是中点,
,
,
,
,
是等边三角形,故③正确;
设,则,
由勾股定理得,,
为中点,
,
,
在中,由勾股定理得,,
四边形是矩形,
,
,故①正确;
,,
,故②错误;
,
,
,故④正确;
综上所述,结论正确是①③④,共3个.
19.B
解:∵
∴
∵四边形与四边形是正方形
∴
∴
∵
∴
∵,
∴
∵四边形+梯形
∴
∴
∴
∵,
∴,即
∵四边形与四边形是正方形
∴,
∴
∴
∴
∴四边形
∵
∴四边形是矩形
∴矩形四边形四边形四边形
∴四边形矩形
20.C
解:∵八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,
∴CG=KG,CF=DG=KF
∴S1=(CG+DG)2
=CG2+DG2+2CG?DG
=GF2+2CG?DG,
S2=GF2=EF2,
S3=(KF﹣NF)2=KF2+NF2﹣2KF?NF,
∴S1+S2+S3=GF2+2CG?DG+GF2+KF2+NF2﹣2KF?NF=3GF2=3EF2=48,
21.4或14
解:如图,当≌时,BP1=CE=1
即3-0.5t=1,解得t=4,
如图,当≌时,CP2=CE=1
即0.5t-6=1,解得t=14,
故答案为:4或14.
22..
解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
∴ME=NE,
∵∠CED=90°,∠DCE=30°,
∴DE=CD=1,CE=,
∵NE=ME,
∴1+DN=-CM,
∴DN=
∴NE=DN+DE=+1=
∵OE=
23.
解:根据折叠的性质,得=8,∵四边形ABCD是矩形,∴CD=AB=4,
在直角三角形中,=,∴∠=30°,
∵根据折叠的性质,四边形ABCD是矩形,∴∠90°,
∴∠=60°,∴∠=30°,∴,
在直角三角形中,,
∵=8-,∴BG==,
24.30
解:如图,延长GB交CD与点H,
∵四边形ABCD是正方形,
∴BA=BC,∠BCH=∠BAE=90°,
∵四边形BEFG是正方形,
∴∠EBG=90°,BE=BG,
∴∠ABE+∠GBC=180°,
又∵∠HBC+∠GBC=180°,
∴∠ABE=∠HBC,
∴△ABE≌△CBH,
∴BH=BE,,
∵BE=BG,
∴BH=BG,
∴,
在Rt△ABE中,,
∵,
∴,
25.
解:∵的面积为m
∴边BC上的高为
如图:当高取最小值时,为等边三角形,A与M或N或MN上一重合重合,
如图:过A作AD⊥BC,垂足为D
∵等边三角形ABC,BC=4
∴∠ABC=60°,BC=4,∠BAD=30°
∴BD=2,
∴AD==2
∴,即m=4;
如图:当高取最大值时,菱形为正方形,
∴A在中点,
∴,即m=8
∴.
26.(1)见详解;(2)
(1)证明:把△ADE绕点D逆时针旋转90°得到△DAH,使得点A与点C重合,如图所示:
由旋转的性质可得DE=DH,∠EDH=90°,AE=CH,
∵∠EDF=45°,
∴∠EDF=∠HDF=45°,
∵DF=DF,
∴△DEF≌△DHF(SAS),
∴FH=EF,
∴EF=HF=FC+CH=AE+FC;
(2)设CF=x,由(1)可得EF=1+x,
∵AB=BC=3,AE=1,
∴BF=3-x,BE=2,
∴在Rt△BEF中,,即,
解得:,
∴.
27.(1)证明见解析;(2)AB=BC
(1)证明:四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∴MN=2OM,
∵
AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)当AB=BC时,四边形AMCN是正方形;
∵AB=BC,四边形ABCD是平行四边形,
∴
四边形ABCD是菱形,
∴
AC⊥BD,
∴AC⊥MN,
由(1)可知四边形ABCD是矩形,
∴四边形ABCD是正方形;
28.证明见解析
证明:∵四边形ABCD为菱形,
∴AD=AB=CD=CB,∠B=∠D.
又∵CE=CF,
∴CB-CE=CD-CF,
即DF=BE.
∴△ABE≌△ADF(SAS).
∴AE=AF.
29.(1)见详解;(2).
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵AB=BC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
又∵AB=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BC,CE=,
∴CD=,
∵四边形ABCD是菱形,
∴BC=CD=,
∵四边形ABCD的面积为4,
∴?DE=4,即:,
∴,
∴DE=或DE=-(舍去),
∴DE=.
30.(1)证明见解析;(2)24.
解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN.
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
31.(1)证明见解析,(2)
28.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFE=∠FEC,
由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,
∴∠AEF=∠AFE,
∴AF=AE,
∴AF=CF=CE=AE,
∴四边形AFCE为菱形.
(2)设AE=x,则BE=7-
x,
,
解得,,(舍去),
平行四边形ABCD的面积为:4×7=28.
(
2
)
(
1
)
一、单选题
1.下列说法中,错误的是(
)
A.对角线互相平分的四边形是平行四边形
B.对角线互相垂直的平行四边形是菱形
C.对角线相等且互相垂直的四边形是正方形
D.对角线相等且互相平分的四边形是矩形
2.正方形?菱形?矩形都具有的性质是(
)
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角线平分一组对角
3.平行四边形的对角线和交于点,添加一个条件不能使平行四边形变为矩形的是(
)
A.
B.
C.
D.
4.如图,在菱形中,点是的中点,点是的中点,连接,如果,那么菱形的周长为( )
A.4
B.8
C.16
D.32
5.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A(﹣3,0),B(2,b),则b的值为( )
A.3
B.2
C.﹣3
D.﹣2
6.如图,在矩形中,点,分别在边和上,把该矩形沿折叠,使点恰好落在边的点处,已知矩形的面积为,,则折痕的长为(
)
A.
B.2
C.
D.4
7.如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若,,则菱形ABCD的周长为( )
A.
B.16
C.
D.32
8.如图,在矩形中,,M为的中点,连接,E为的中点,连接、,若为直角,则的值为(
)
A.3
B.
C.
D.
9.如图,在菱形中,,E、F分别是边、的中点,于点P,则的度数是(
).
A.50°
B.45°
C.40°
D.30°
10.如图,在正方形ABCD中,E、F分别是BC、CD上的点,若△AEF是边长为2的等边三角形,则正方形的边长是( )
A.
B.+1
C.
D.
11.如图,将矩形纸片沿其对角线折叠,使点落到点的位置,与交于点,若,,则图中阴影部分的周长为(
)
A.10
B.13
C.17
D.20
12.如图,矩形纸片,,,点在边上.将沿折叠,点落在点处.、分别交于点、,且.则的长为(
)
A.2
B.
C.
D.
13.如图,E、F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是(
)
A.α=β
B.α=γ
C.α+β+2γ=90°
D.2α+γ=90°
14.如图,O是菱形的对角线的交点,E,F分别是的中点给出下列结论:①;②四边形也是菱形;③四边形的面积大小等于;④;⑤是轴对称图形.其中正确的结论有(
)
A.2个
B.3个
C.4个
D.5个
15.如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果∠ADB=40°,则∠E的度数是(
)
A.10°
B.20°
C.30°
D.40°
16.如图,在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE//AC,DF//AB,分别交AB、AC于E、F两点,下列说法错误的是(
)
A.四边形AEDF是平行四边形
B.若AD平分∠BAC,则四边形AEDF是菱形
C.若AB⊥AC,则四边形AEDF是矩形
D.若BD=CD,则四边形AEDF是正方形
17.如图,点P为正方形内一点,已知正方形的边长为2,且有,则的最小值为(
).
A.1
B.
C.
D.
18.如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于E,点G是AE中点且∠AOG=30°,①DC=3OG;②OG=BC;③△OGE是等边三角形;④S△AOE=S矩形ABCD,则下列结论正确的个数为( )
A.1个
B.2个
C.3个
D.4个
19.如图,在中,,以的各边为边分别作正方形,正方形与正方形.延长,分别交,于点,,连结,.图中两块阴影部分面积分别记为,,若,四边形,则四边形的面积为(
)
A.5
B.6
C.8
D.9
20.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)所示).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成的记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若EF=4,则S1+S2+S3的值是( )
A.32
B.38
C.48
D.80
二、填空题
21.如图,在正方形中,,延长到点E,使,连接,动点P从点A出发,以每秒的速度沿向终点A运动.设点P的运动时间为t秒,当和全等时,t的值为__________.
22.如图,ABCD为正方形,O为AC、BD的交点,△DCE为直角三角形,∠CED=90°,∠DCE=30°,若正方形的边长为2,则OE的长为__________.
23.如图,ABCD是一张长方形纸片,且AD=2AB=8,沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′)折痕交于点G,则BG=______.
24.如图,点为正方形的边的延长线上一点,以为边在的另一侧作正方形,连接,若,,则的面积为______.
25.对于任意三角形,如果存在一个菱形,使得这个菱形的一条边与三角形的一条边重合,且三角形的这条边所对的顶点在菱形的这条边的对边上,那么称这个菱形为该三角形的“最优覆盖菱形”.问题:如图,在中,,,且的面积为m,如果存在“最优覆盖菱形”为菱形,那么m的取值范围是________.
三、解答题
26.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.
(1)求证:EF=AE+CF
(2)当AE=1时,求EF的长.
27.如图,已知平行四边形ABCD,若M,N是BD上两点,且BM=DN,AC=2OM,
(1)求证:四边形
AMCN
是矩形;
(2)△ABC
满足什么条件,四边形AMCN是正方形,请说明理由.
28.已知:如图,在菱形中,E,F分别在边,上,且,求证:.
29.如图,在四边形ABCD中,AD∥BC,AB=BC,BD平分∠ABC.过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若CE=,四边形ABCD的面积为4,求DE的长.
30.如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.
(1)求证:△AMB≌△CND;
(2)若BD=2AB,且AB=5,DN=4,求四边形DEMN的面积.
31.如图,将平行四边形ABCD折叠,使点C与点A重合,折痕EF交BC于E交AD于F,交AC于G,连接AE,CF.
(1)求证:四边形AECF为菱形;
(2)若四边形AECF恰为正方形,且AB=5,BC=7,求平行四边形ABCD的面积.
(
2
)
(
1
)
参考答案
1.C
解:A.对角线互相平分的四边形是平行四边形,此说法正确,不符合题意;
B.对角线互相垂直的平行四边形是菱形,此说法正确,不符合题意;
C.对角线相等且互相垂直的平行四边形是正方形,故原说法错误,符合题意;
D.对角线相等且互相平分的四边形是矩形,此说法正确,不符合题意.
2.B
解:∵正方形的对角线互相平分,互相垂直,相等且平分一组对角,
菱形的对角线互相平分,互相垂直且平分一组对角,
矩形的对角线互相平分且相等,
∴正方形、菱形、矩形都具有的性质是:对角线互相平分.
3.D
解:∵四边形是平行四边形,
∴,,
A.
时,,
∴平行四边形是矩形,故选项A不符合题意;
B.四边形是平行四边形,,
∴平行四边形是矩形,故选项B不符合题意;
C.∵,
∴,
∴,
∴平行四边形是矩形,故选项C不符合题意;
D.四边形是平行四边形,,
∴平行四边形是菱形,故选项D符合题意;
4.D
解:∵E为AB中点,F为AC中点,
∴线段EF为的中位线,
∴.
∵四边形ABCD为菱形,
∴该菱形的周长=4×8=32.
5.C
解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
在△DAO和△ABM中,
,
∴△DAO≌△ABM(AAS),
∴BM=OA,
∵A(,0),B(2,b),
∴BM=OA=3,
∴b=.
6.D
解:
由折叠的性质可知,BE=EH,AF=FG,GH=AB,∠BEF=∠HEF,
∵∠BEF+∠HEF=180°-∠HEC=120°,
∴∠HEF=60°
∵FH∥CE,∠HEC=60°,
∴∠FHE=∠HEC=60°,
∴△HEF为等边三角形,
∴EF=HE=FH,
∵∠FHE=60°,∠B=∠GHE=∠FHE+∠GHF=90°,
∴∠GHF=30°,
在Rt△FGH中,∠GHF=30°,
∴FH=2FG=2AF,
∴设FG=x,则FH=2x,HD=x,
则有,
∴AD=AF+FH+HD=4x,
又∵矩形ABCD的面积为,
∴,
∴x=2或x=-2(舍),
∴EF=FH=4,
7.C
解:∵E,F分别是AB,BC边上的中点,EF=,
∴AC=2EF=,
∵四边形ABCD是菱形,,
∴AC⊥BD,OA=AC=,OB=BD=4,
∴AB==,
∴菱形ABCD的周长为:=.
8.D
解:连接AE,过点E作EF⊥AD,并延长,交BC于点H,如图所示:
∵四边形是矩形,,
∴,,,,
∴,
∴四边形是矩形,
∵E为的中点,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵M为的中点,
∴,
∴,
∴,
∴;
9.A
解:延长PF交AB的延长线于点G.如图所示:
∵四边形ABCD是菱形,
∴AB∥CD,
∴∠GBF=∠PCF,
∵F是边BC的中点,
∴BF=CF,
在△BGF与△CPF中,
∴△BGF≌△CPF(ASA)
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEP=90°,
∴EF=PG,
∵PF=PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP-∠FEP=∠EPC-∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°-∠A=80°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=
(180°-80°)=50°,
∴∠FPC=50°;
10.D
解:由题知:△AEF是边长为2的等边三角形,
∴∠EAF=60°,AE=AF,∴∠BAE+∠DAF=30°,
又AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF=15°,
如图,作∠AEH=∠BAE=15°,交AB于H,
∴∠BHE=30°,AH=HE,∴HE=2BE=AH,BH=BE,∴AB=(2+)BE,
∵AE2=BE2+AB2,
∴4=BE2+(2+)2×BE2,
∴BE=(﹣1)=,
∴AB=(2+)BE=,
11.D
解:∵四边形ABCD为矩形,
∴B′C=BC=AD,∠B′=∠B=∠D=90°,
∵∠B′EC=∠DEA,
在△AED和△CEB′中,
,
∴△AED≌△CEB′(AAS);
∴EA=EC,
∴阴影部分的周长为AD+DE+EA+EB′+B′C+EC
=AD+DE+EC+EA+EB′+B′C
=AD+DC+AB′+B′C
=3+7+7+3
=20,
12.B
解:∵四边形ABCD是矩形
∴,,
根据折叠的性质,得:,,
在与中
∴
∴,
∴
设,则
∴
∴
在中,由勾股定理得:
解得:
即
13.B
解:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵∠ADE=α,∠EDF=β,∠FDC=γ,
∴α+β+γ=90°,
∵∠AED+α=90°,∠AED=α+β,
∴2α+β=90°,
∴α+β+γ=2α+β,
∴α=γ,
14.C
解:①正确
∵E、F分别是OA、OC的中点.
∴AE=OE.
∵S△ADEAE×ODOE×OD=S△EOD
∴S△ADE=S△EOD.
②正确
∵四边形ABCD是菱形,E,F分别是OA,OC的中点.
∴EF⊥OD,OE=OF.
∵OD=OB.
∴四边形BFDE是菱形.
③正确
∵菱形ABCD的面积AC×BD.
∵E、F分别是OA、OC的中点.
∴EFAC.
∴菱形ABCD的面积=EF×BD.
④不正确
由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.
⑤正确
∵EF⊥OD,OE=OF,OD=OD.
∴△DEO≌△DFO.
∴△DEF是轴对称图形.
∴正确的结论有四个,分别是①②③⑤,
15.B
解:连接AC,交BD于点O,
∵四边形ABCD是矩形,
∴AC=BD,
∵EC=BD,
∴AC=CE,
∴∠E=∠CAE,
∵OB=OC,
∴∠ACB=∠DBC,
又∵AD∥BC,
∴∠DBC=∠ADB,
∴∠ACB=∠ADB=40°,
∵∠ACB=∠E+∠CAE,
∴∠E=∠CAE=20°,
16.D
解:∵DE//AC,DF//AB,
∴四边形AEDF是平行四边形,故选项A正确,不符合题意;
若AD平分∠BAC,则∠EAD=∠FAD,
又∵∠EAD=∠FDA,
∴∠FAD=∠FDA
,∴FA=FD,
∴平行四边形AEDF是菱形,
故选项B正确,不符合题意;
∵AB⊥AC,
∴平行四边形AEDF是矩形,
故选项C正确,不符合题意;
若BD=CD,则四边形AEDF不一定是正方形;选项D错误,符合题意.
17.C
解:取AD中点E,连接PE、BE,
∵正方形的边长为2,
∴PE=AE=1,
,
∵,
当P、E、B三点共线时,最小,最小值为,
18.C
解:,点是中点,
,
,
,
,
是等边三角形,故③正确;
设,则,
由勾股定理得,,
为中点,
,
,
在中,由勾股定理得,,
四边形是矩形,
,
,故①正确;
,,
,故②错误;
,
,
,故④正确;
综上所述,结论正确是①③④,共3个.
19.B
解:∵
∴
∵四边形与四边形是正方形
∴
∴
∵
∴
∵,
∴
∵四边形+梯形
∴
∴
∴
∵,
∴,即
∵四边形与四边形是正方形
∴,
∴
∴
∴
∴四边形
∵
∴四边形是矩形
∴矩形四边形四边形四边形
∴四边形矩形
20.C
解:∵八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,
∴CG=KG,CF=DG=KF
∴S1=(CG+DG)2
=CG2+DG2+2CG?DG
=GF2+2CG?DG,
S2=GF2=EF2,
S3=(KF﹣NF)2=KF2+NF2﹣2KF?NF,
∴S1+S2+S3=GF2+2CG?DG+GF2+KF2+NF2﹣2KF?NF=3GF2=3EF2=48,
21.4或14
解:如图,当≌时,BP1=CE=1
即3-0.5t=1,解得t=4,
如图,当≌时,CP2=CE=1
即0.5t-6=1,解得t=14,
故答案为:4或14.
22..
解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,
∵∠CED=90°,
∴四边形OMEN是矩形,
∴∠MON=90°,
∵∠COM+∠DOM=∠DON+∠DOM,
∴∠COM=∠DON,
∵四边形ABCD是正方形,
∴OC=OD,
在△COM和△DON中,
∴△COM≌△DON(AAS),
∴OM=ON,
∴四边形OMEN是正方形,
∴ME=NE,
∵∠CED=90°,∠DCE=30°,
∴DE=CD=1,CE=,
∵NE=ME,
∴1+DN=-CM,
∴DN=
∴NE=DN+DE=+1=
∵OE=
23.
解:根据折叠的性质,得=8,∵四边形ABCD是矩形,∴CD=AB=4,
在直角三角形中,=,∴∠=30°,
∵根据折叠的性质,四边形ABCD是矩形,∴∠90°,
∴∠=60°,∴∠=30°,∴,
在直角三角形中,,
∵=8-,∴BG==,
24.30
解:如图,延长GB交CD与点H,
∵四边形ABCD是正方形,
∴BA=BC,∠BCH=∠BAE=90°,
∵四边形BEFG是正方形,
∴∠EBG=90°,BE=BG,
∴∠ABE+∠GBC=180°,
又∵∠HBC+∠GBC=180°,
∴∠ABE=∠HBC,
∴△ABE≌△CBH,
∴BH=BE,,
∵BE=BG,
∴BH=BG,
∴,
在Rt△ABE中,,
∵,
∴,
25.
解:∵的面积为m
∴边BC上的高为
如图:当高取最小值时,为等边三角形,A与M或N或MN上一重合重合,
如图:过A作AD⊥BC,垂足为D
∵等边三角形ABC,BC=4
∴∠ABC=60°,BC=4,∠BAD=30°
∴BD=2,
∴AD==2
∴,即m=4;
如图:当高取最大值时,菱形为正方形,
∴A在中点,
∴,即m=8
∴.
26.(1)见详解;(2)
(1)证明:把△ADE绕点D逆时针旋转90°得到△DAH,使得点A与点C重合,如图所示:
由旋转的性质可得DE=DH,∠EDH=90°,AE=CH,
∵∠EDF=45°,
∴∠EDF=∠HDF=45°,
∵DF=DF,
∴△DEF≌△DHF(SAS),
∴FH=EF,
∴EF=HF=FC+CH=AE+FC;
(2)设CF=x,由(1)可得EF=1+x,
∵AB=BC=3,AE=1,
∴BF=3-x,BE=2,
∴在Rt△BEF中,,即,
解得:,
∴.
27.(1)证明见解析;(2)AB=BC
(1)证明:四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
∴MN=2OM,
∵
AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)当AB=BC时,四边形AMCN是正方形;
∵AB=BC,四边形ABCD是平行四边形,
∴
四边形ABCD是菱形,
∴
AC⊥BD,
∴AC⊥MN,
由(1)可知四边形ABCD是矩形,
∴四边形ABCD是正方形;
28.证明见解析
证明:∵四边形ABCD为菱形,
∴AD=AB=CD=CB,∠B=∠D.
又∵CE=CF,
∴CB-CE=CD-CF,
即DF=BE.
∴△ABE≌△ADF(SAS).
∴AE=AF.
29.(1)见详解;(2).
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵AB=BC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
又∵AB=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BC,CE=,
∴CD=,
∵四边形ABCD是菱形,
∴BC=CD=,
∵四边形ABCD的面积为4,
∴?DE=4,即:,
∴,
∴DE=或DE=-(舍去),
∴DE=.
30.(1)证明见解析;(2)24.
解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点M,N分别为OA、OC的中点,
∴AM=CN,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAM=∠DCN,
∴△AMB≌△CND(SAS);
(2)∵△AMB≌△CND,
∴BM=DN,∠ABM=∠CDN,
又∵BM=EM,
∴DN=EM,
∵AB∥CD,
∴∠ABO=∠CDO,
∴∠MBO=∠NDO,
∴ME∥DN.
∴四边形DEMN是平行四边形,
∵BD=2AB,BD=2BO,
∴AB=OB,
又∵M是AO的中点,
∴BM⊥AO,
∴∠EMN=90°,
∴四边形DEMN是矩形,
∵AB=5,DN=BM=4,
∴AM=3=MO,
∴MN=6,
∴矩形DEMN的面积=6×4=24.
31.(1)证明见解析,(2)
28.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFE=∠FEC,
由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,
∴∠AEF=∠AFE,
∴AF=AE,
∴AF=CF=CE=AE,
∴四边形AFCE为菱形.
(2)设AE=x,则BE=7-
x,
,
解得,,(舍去),
平行四边形ABCD的面积为:4×7=28.
(
2
)
(
1
)
