2020-2021学年人教版数学七年级下册:6.1.1 算术平方根 课件(23张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册:6.1.1 算术平方根 课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
6.1.1
算术平方根
人教版数学七年级下册
第六章
实
数
理解算术平方根的概念,会用根号表示正数的算术平方根。
理解算术平方根的非负性。
通过平方运算求某些非负数的算术平方根。
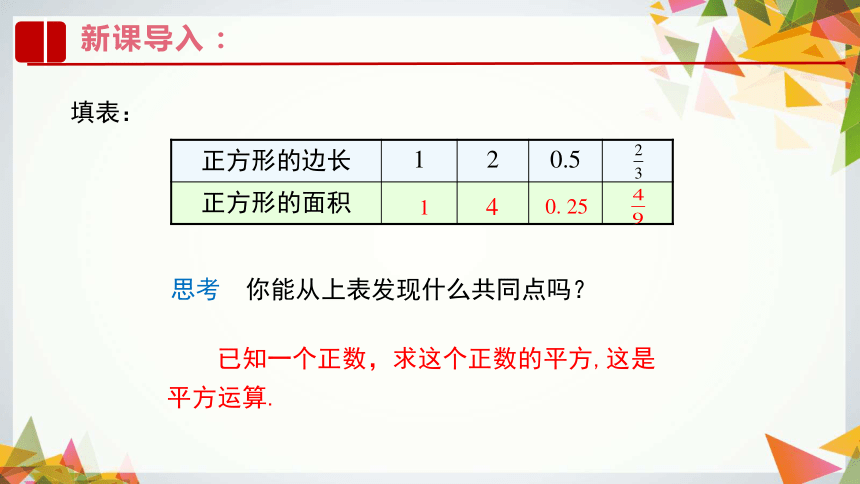
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长
1
2
0.5
正方形的面积
1
填表:
思考
你能从上表发现什么共同点吗?
4
0.
25
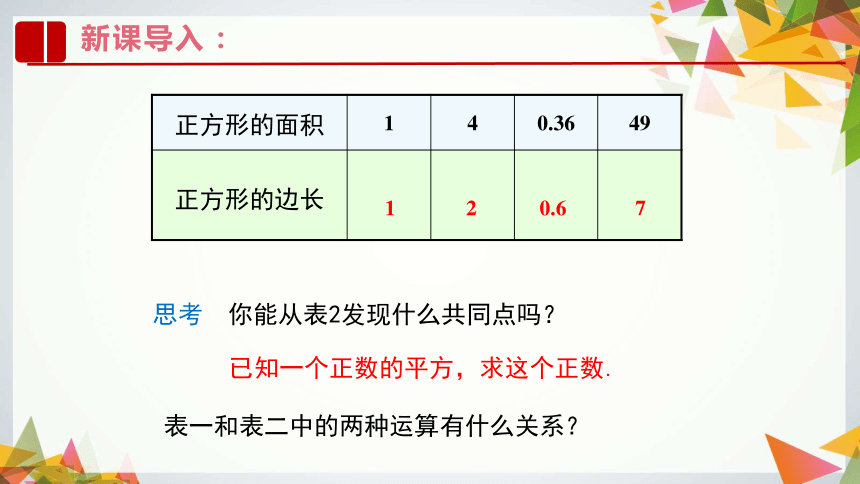
正方形的面积
1
4
0.36
49
正方形的边长
已知一个正数的平方,求这个正数.
表一和表二中的两种运算有什么关系?
1
2
0.6
7
思考
你能从表2发现什么共同点吗?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做
a的算术平方根.
1.因为22=4
,所以4的算术平方根是__;
2
2.下列说法正确的是
.
①5是25的算术平方根.
②
0.01是0.1的算术平方根.
①
【针对练习】
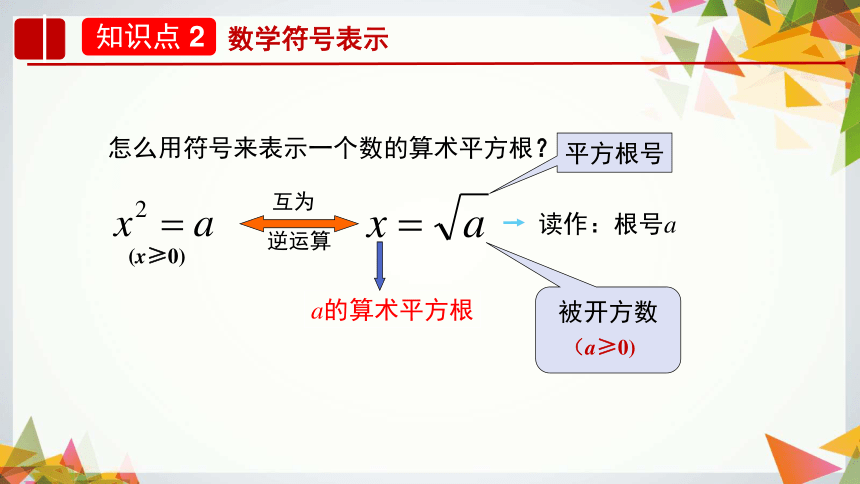
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有1个
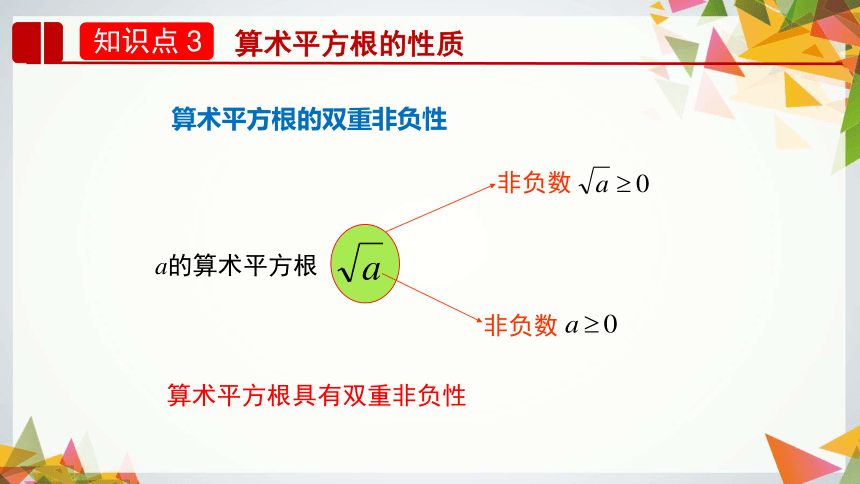
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
算术平方根的双重非负性
算术平方根
根号a
被开方数
0
例1
分别求下列各数的算术平方根:
(1)100,
(2)
,
(3)
解:(1)由于102=100,
因此
;
(2)由于
2=
,
因此
;
(3)由于0.72=0.49,
因此
.
不难看出:被开方数越大,对应的算术平方根也越大.
例2
计算:
(1)
;
(2)
.
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
1)16的算术平方根是______;
4
2
2)
的算术平方根是______;
例3
填空:
【点睛】注意文字或算术的表述,读清题意,再进行计算,以防误解.
解:
无意义,因为被开方数不是非负数.
下列各式中哪些有意义?哪些无意义?为什么?
注意:被开方数为非负数.
解:
因为|m-1|
≥0,
≥0,又|m-1|
+
=0,
所以
|m-1|
=0,
=0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
例4
若|m-1|
+
=0,求m+n的值.
【点睛】几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
3.若
,则a=
;
2.若
,则m=
;
4.若|a-3|+
,则代数式
=___.
1.若|a+3|=0
,
则a=
;
-3
7
5
-1
到目前为止,表示非负数的式子有:
a≥0,
|a|≥0,
a2
≥0,
≥0,
例5:自由下落物体下落的距离h(米)与下落时间t(秒)的关系为
有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将h=19.6代入公式
,
得
,
所以正数
(秒).
即铁球到达地面需要2秒.
1.若,则
=______.
【详解】
解:∵,
∴,
∴,
故答案为:.
变式
若,则_____.
【详解】
解:∵,
∴x+1=3,即x=2.
故答案为:2
的算术平方根是(
)
A.
B.
C.
D.5
【答案】B
【详解】
∵=5,
∴5的算术平方根是
∴的算术平方根是,
故选B.
3.
的算术平方根是(
)
A.9
B.3
C.
D.-3
【答案】B
【详解】
解:,
的算术平方根是3.
故选:.
4.已知a是最小正整数,b是的算术平方根,则a+b的值是_____.
【详解】
∵a是最小正整数,
∴a=1,
∵=9,b是的算术平方根,
∴b==3,
∴a+b=1+3=4.
故答案为:4
5.计算若,那么a2019
b2020=____________.
【详解】
∵,
∴(a+1)2=0,b-1=0,
解得:a=-1,b=1,
∴a2019+b2020=-1+1=0,
故答案为:0
谢谢观看
6.1.1
算术平方根
人教版数学七年级下册
第六章
实
数
理解算术平方根的概念,会用根号表示正数的算术平方根。
理解算术平方根的非负性。
通过平方运算求某些非负数的算术平方根。
已知一个正数,求这个正数的平方,这是平方运算.
正方形的边长
1
2
0.5
正方形的面积
1
填表:
思考
你能从上表发现什么共同点吗?
4
0.
25
正方形的面积
1
4
0.36
49
正方形的边长
已知一个正数的平方,求这个正数.
表一和表二中的两种运算有什么关系?
1
2
0.6
7
思考
你能从表2发现什么共同点吗?
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做
a的算术平方根.
1.因为22=4
,所以4的算术平方根是__;
2
2.下列说法正确的是
.
①5是25的算术平方根.
②
0.01是0.1的算术平方根.
①
【针对练习】
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有1个
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
算术平方根的双重非负性
算术平方根
根号a
被开方数
0
例1
分别求下列各数的算术平方根:
(1)100,
(2)
,
(3)
解:(1)由于102=100,
因此
;
(2)由于
2=
,
因此
;
(3)由于0.72=0.49,
因此
.
不难看出:被开方数越大,对应的算术平方根也越大.
例2
计算:
(1)
;
(2)
.
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
1)16的算术平方根是______;
4
2
2)
的算术平方根是______;
例3
填空:
【点睛】注意文字或算术的表述,读清题意,再进行计算,以防误解.
解:
无意义,因为被开方数不是非负数.
下列各式中哪些有意义?哪些无意义?为什么?
注意:被开方数为非负数.
解:
因为|m-1|
≥0,
≥0,又|m-1|
+
=0,
所以
|m-1|
=0,
=0,所以m=1,n=-3,
所以m+n=1+(-3)=-2.
例4
若|m-1|
+
=0,求m+n的值.
【点睛】几个非负数的和为0,则每个数均为0,初中阶段学过的非负数有绝对值、偶次幂及一个数的算术平方根.
3.若
,则a=
;
2.若
,则m=
;
4.若|a-3|+
,则代数式
=___.
1.若|a+3|=0
,
则a=
;
-3
7
5
-1
到目前为止,表示非负数的式子有:
a≥0,
|a|≥0,
a2
≥0,
≥0,
例5:自由下落物体下落的距离h(米)与下落时间t(秒)的关系为
有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将h=19.6代入公式
,
得
,
所以正数
(秒).
即铁球到达地面需要2秒.
1.若,则
=______.
【详解】
解:∵,
∴,
∴,
故答案为:.
变式
若,则_____.
【详解】
解:∵,
∴x+1=3,即x=2.
故答案为:2
的算术平方根是(
)
A.
B.
C.
D.5
【答案】B
【详解】
∵=5,
∴5的算术平方根是
∴的算术平方根是,
故选B.
3.
的算术平方根是(
)
A.9
B.3
C.
D.-3
【答案】B
【详解】
解:,
的算术平方根是3.
故选:.
4.已知a是最小正整数,b是的算术平方根,则a+b的值是_____.
【详解】
∵a是最小正整数,
∴a=1,
∵=9,b是的算术平方根,
∴b==3,
∴a+b=1+3=4.
故答案为:4
5.计算若,那么a2019
b2020=____________.
【详解】
∵,
∴(a+1)2=0,b-1=0,
解得:a=-1,b=1,
∴a2019+b2020=-1+1=0,
故答案为:0
谢谢观看
