2012年中考数学专题复习(八):数形结合
文档属性
| 名称 | 2012年中考数学专题复习(八):数形结合 |  | |
| 格式 | zip | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-03 18:37:03 | ||
图片预览


文档简介
数形结合
【知识要点】
数学家华罗庚说得好:“数形结合百般好,隔离分家万事休,几何代数统一体,永远联系莫分离”.几何图形的形象直观,便于理解,代数方法的一般性,解题过程的机械化,可操作性强,便于把握,因此数形结合思想是数学中重要的思想方法.
所谓数形结合就是根据数学问题的题设和结论之间的内在联系,既分析其数量关系,又揭示其几何意义使数量关系和几何图形巧妙地结合起来,并充分地利用这种结合,探求解决问题的思路,使问题得以解决的思考方法.
数形结合是一个数学思想方法,包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:Ⅰ、借助形的生动和直观性来阐明数之间的联系,即以形作为手段,数为目的,比如应用函数的图像来直观地说明函数的性质;Ⅱ、借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质
【历年考卷形势分析及中考预测】
数形结合思想是历年来中考和竞赛的必考内容,纵观近6年广州市的中考试题,分值分布大约在15分左右,其中简单的题目大约占9分,主要考察不等式组的解法,绝对值的化简,勾股定理的应用等等,其余的6分较难,主要出现在后面的压轴题目中,经常和实际问题,动点问题及函数问题结合,难度较大,应引起同学们的高度重视。
【考点精析】
考点1. 借助数轴解不等式及根式的化简:
例1.(2010浙江金华)如图,若A是实数a在数轴上对应的点,则关于a,-a,1的大小关系表示正确的是( )
A.a<1<-a B.a<-a<1
C.1<-a<a D.-a<a<1
例2.如果不等式的整数解仅为1,2,3,那么适合不等式组的整数的有序数对 有多少对?
【举一反三】
1.(2010湖北宜昌)如图,数轴上A,B两点分别对应实数a,b,则下列结论正确的是( )。
A. |a|>|b| B. a+b>0
C. ab<0 D. |b|=b
2.如果关于x的不等式组的解 有解,求m的取值范围
考点2. 借助平面直角坐标系解函数问题:
例3.(2010 浙江台州市)类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
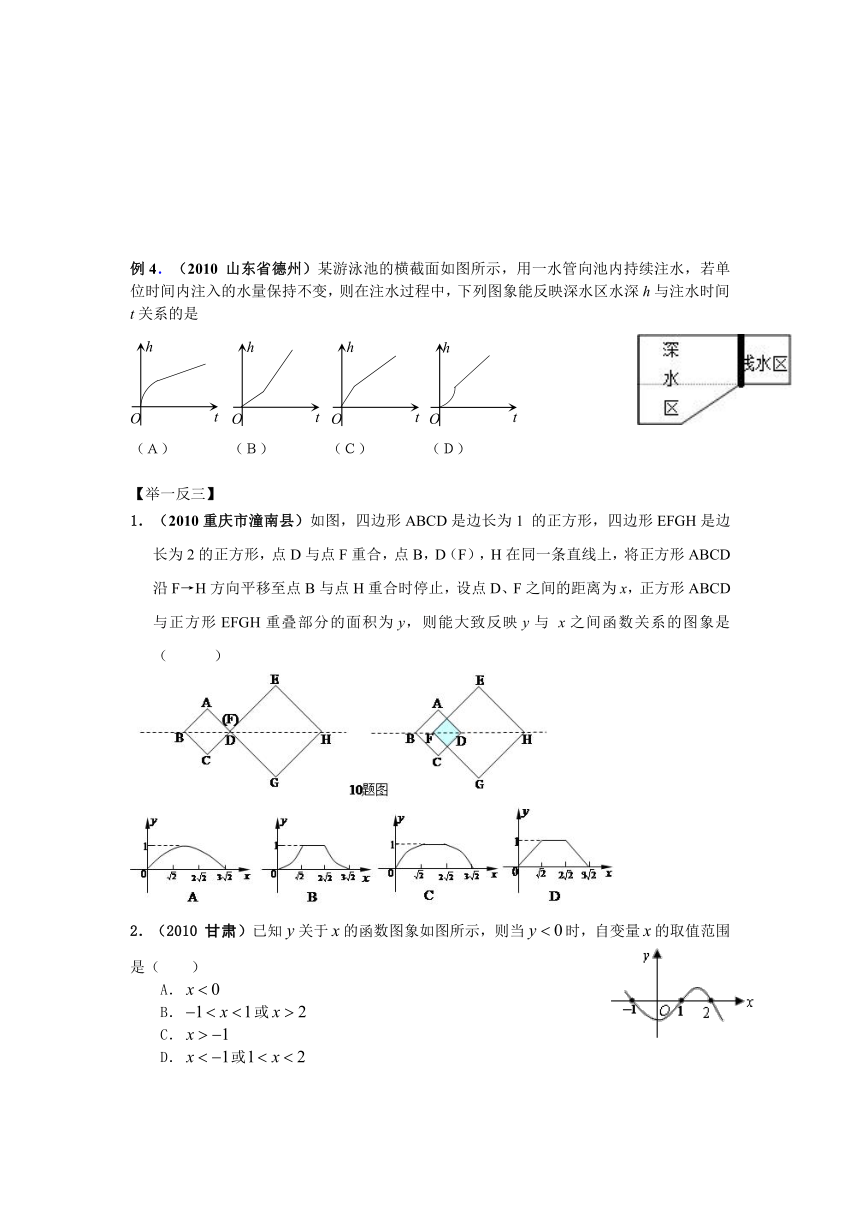
例4.(2010 山东省德州)某游泳池的横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反映深水区水深h与注水时间t关系的是
(A) (B) (C) (D)
【举一反三】
1.(2010重庆市潼南县)如图,四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H方向平移至点B与点H重合时停止,设点D、F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与 x之间函数关系的图象是( )
2.(2010 甘肃)已知关于的函数图象如图所示,则当时,自变量的取值范围是( )
A.
B.或
C.
D.或
考点3. 利用图形理解代数恒等式
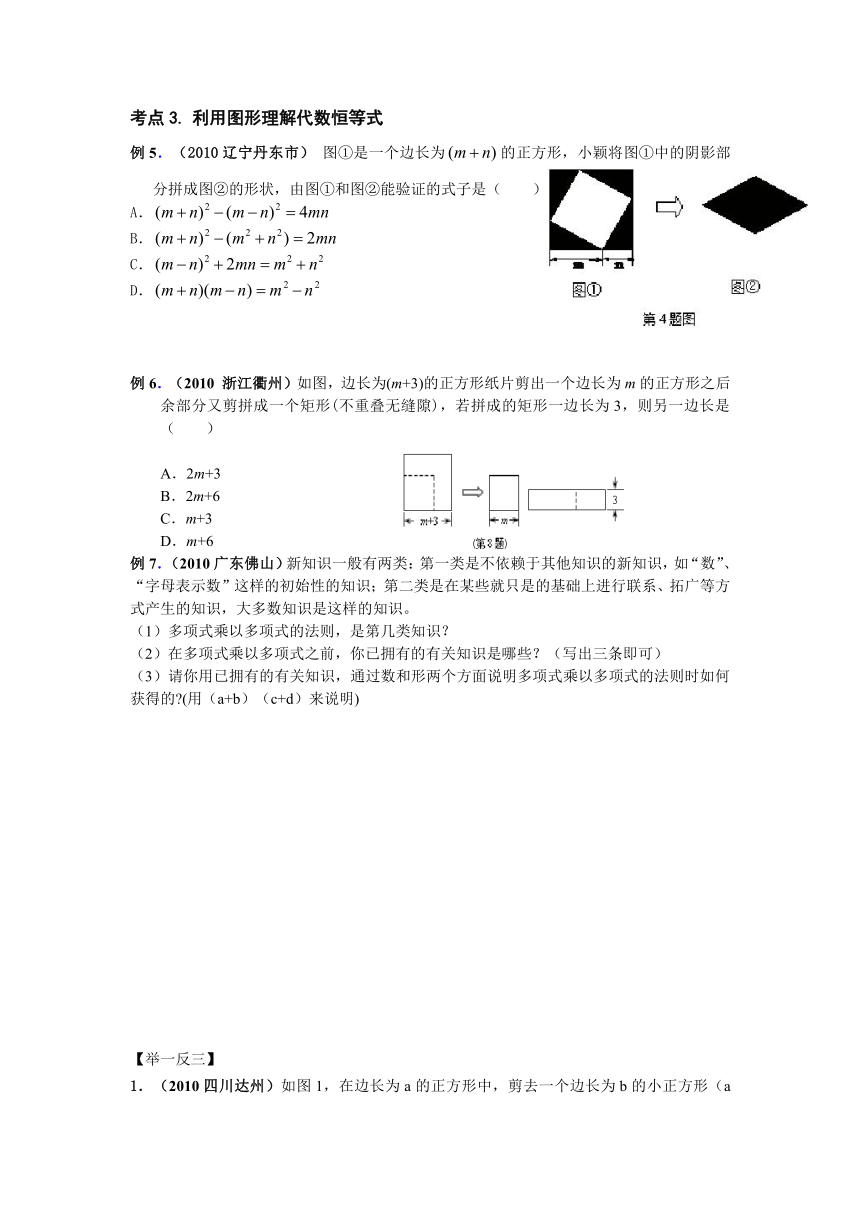
例5.(2010辽宁丹东市) 图①是一个边长为的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A.
B.
C.
D.
例6.(2010 浙江衢州)如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )
A.2m+3
B.2m+6
C.m+3
D.m+6
例7.(2010广东佛山)新知识一般有两类:第一类是不依赖于其他知识的新知识,如“数”、“字母表示数”这样的初始性的知识;第二类是在某些就只是的基础上进行联系、拓广等方式产生的知识,大多数知识是这样的知识。
(1)多项式乘以多项式的法则,是第几类知识?
(2)在多项式乘以多项式之前,你已拥有的有关知识是哪些?(写出三条即可)
(3)请你用已拥有的有关知识,通过数和形两个方面说明多项式乘以多项式的法则时如何获得的 (用(a+b)(c+d)来说明)
【举一反三】
1.(2010四川达州)如图1,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为
A. B.
C. D.
2.(2010浙江湖州)将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系得到的数学公式是 .
考点4.借助直角三角形解三角比问题
例8.(南京·2007中考)如图,A、B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A—C—B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米 (结果精确到0.1km)(参考数据:,)
考点5.借助勾股定理等几何图形的知识解实际问题
例9.(上海·2006中考)本市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取A、B、C三根木柱,使得A、B之间的距离与A、C之间的距离相等,并测得BC长为240米,A到BC的距离为5米,如图1所示.请你帮他们求出滴水湖的半径.
【举一反三】
气象台发布的卫星云图显示,代号为W的台风在某海岛(设为点O)的南偏东45°方向的B点生成,测得OB=100√6km.台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处.因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西60°方向继续移动.以O为原点建立如图所示的直角坐标系.
(1)台风生成中心点B的坐标为 ______ ,台风中心转折点C的坐标为 _____ (结果保留根号)
(2)已知距台风中心20km的范围内均会受到台风的侵袭.如果某城市(设为点A)位于点O的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
考点6.借助图形解决代数式或函数最值问题
例10.解关于x的方程
例11.已知,求S的最小值。
【举一反三】
1 解关于x的方程
考点7.借助图形解决函数解析式问题
例12 在同一坐标系内,直线l1:y=(k-2)x+k和l2:y=kx的位置可能为( )
例13.如果一次函数的图象经过第二、三、四象限,那么( )
(A)且 (B)且
(C)且 (D)且
例14.一次函数与,它们在同一坐标系内的大致图象是( )
【举一反三】
1 一次函数y=kx+b的图象经过点(m,1)和(-1,m)其中m>-1则k、b应满足( )
(A)k>0且b>0 (B)k>0且b<0
(C)k<0且b>0 (D)k<0且b<0
2 如果函数y=kx+b的图象在第一、二、三象限内,那么函数y=kx2+bx-1的图象大致是( )
3 当时,反比例函数和一次函数的图象大致是( )
考点8.借助图形解决实际问题
例15.(09年北京)如图,A、B两点在函数的图象上.
(1)求的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数。
【举一反三】
1 某商业公司为指导某种应季商品的生产和销售,对二月份至七月份的该商品的销售和成本进行了调研,结果如下:每件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图),每件商品的成本Q(元)与时间t的关系可用一条抛物线的一部分上的点来表示(如图)(说明:图①、图②中的每一个实心黑点所对应的纵坐标,分别指相应月份的售价和成本)
请你根据图像提供的信息回答:
(1)每件商品在3月份出售时的利润(利润=售价-成本)是多少元?
(2)求图中表示的每件商品的成本Q(元)与时间t(月)之间的函数关系式(不要求写出自变量的取值范围)
(3)你能求出三月份至七月份每件商品的利润W(元)与时间t(月)之间的函数关系式吗?(请写出计算过程,不要求写自变量的取值范围)若该公司共有此种商品30000件,准备在一个月内全部售完,请你计算一下至少可获利多少元?
0
1
A
(第9题图)
(第4题)
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
t
h
O
t
h
O
t
h
O
h
t
O
图1
A
B
C
30°
45°
3图
·
·
·
A
B
C
例4图2
·
O
D
A
B
C
D
【知识要点】
数学家华罗庚说得好:“数形结合百般好,隔离分家万事休,几何代数统一体,永远联系莫分离”.几何图形的形象直观,便于理解,代数方法的一般性,解题过程的机械化,可操作性强,便于把握,因此数形结合思想是数学中重要的思想方法.
所谓数形结合就是根据数学问题的题设和结论之间的内在联系,既分析其数量关系,又揭示其几何意义使数量关系和几何图形巧妙地结合起来,并充分地利用这种结合,探求解决问题的思路,使问题得以解决的思考方法.
数形结合是一个数学思想方法,包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:Ⅰ、借助形的生动和直观性来阐明数之间的联系,即以形作为手段,数为目的,比如应用函数的图像来直观地说明函数的性质;Ⅱ、借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质
【历年考卷形势分析及中考预测】
数形结合思想是历年来中考和竞赛的必考内容,纵观近6年广州市的中考试题,分值分布大约在15分左右,其中简单的题目大约占9分,主要考察不等式组的解法,绝对值的化简,勾股定理的应用等等,其余的6分较难,主要出现在后面的压轴题目中,经常和实际问题,动点问题及函数问题结合,难度较大,应引起同学们的高度重视。
【考点精析】
考点1. 借助数轴解不等式及根式的化简:
例1.(2010浙江金华)如图,若A是实数a在数轴上对应的点,则关于a,-a,1的大小关系表示正确的是( )
A.a<1<-a B.a<-a<1
C.1<-a<a D.-a<a<1
例2.如果不等式的整数解仅为1,2,3,那么适合不等式组的整数的有序数对 有多少对?
【举一反三】
1.(2010湖北宜昌)如图,数轴上A,B两点分别对应实数a,b,则下列结论正确的是( )。
A. |a|>|b| B. a+b>0
C. ab<0 D. |b|=b
2.如果关于x的不等式组的解 有解,求m的取值范围
考点2. 借助平面直角坐标系解函数问题:
例3.(2010 浙江台州市)类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+()=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.
例4.(2010 山东省德州)某游泳池的横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反映深水区水深h与注水时间t关系的是
(A) (B) (C) (D)
【举一反三】
1.(2010重庆市潼南县)如图,四边形ABCD是边长为1 的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B,D(F),H在同一条直线上,将正方形ABCD沿F→H方向平移至点B与点H重合时停止,设点D、F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与 x之间函数关系的图象是( )
2.(2010 甘肃)已知关于的函数图象如图所示,则当时,自变量的取值范围是( )
A.
B.或
C.
D.或
考点3. 利用图形理解代数恒等式
例5.(2010辽宁丹东市) 图①是一个边长为的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
A.
B.
C.
D.
例6.(2010 浙江衢州)如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )
A.2m+3
B.2m+6
C.m+3
D.m+6
例7.(2010广东佛山)新知识一般有两类:第一类是不依赖于其他知识的新知识,如“数”、“字母表示数”这样的初始性的知识;第二类是在某些就只是的基础上进行联系、拓广等方式产生的知识,大多数知识是这样的知识。
(1)多项式乘以多项式的法则,是第几类知识?
(2)在多项式乘以多项式之前,你已拥有的有关知识是哪些?(写出三条即可)
(3)请你用已拥有的有关知识,通过数和形两个方面说明多项式乘以多项式的法则时如何获得的 (用(a+b)(c+d)来说明)
【举一反三】
1.(2010四川达州)如图1,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为
A. B.
C. D.
2.(2010浙江湖州)将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系得到的数学公式是 .
考点4.借助直角三角形解三角比问题
例8.(南京·2007中考)如图,A、B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A—C—B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米 (结果精确到0.1km)(参考数据:,)
考点5.借助勾股定理等几何图形的知识解实际问题
例9.(上海·2006中考)本市新建的滴水湖是圆形人工湖.为测量该湖的半径,小杰和小丽沿湖边选取A、B、C三根木柱,使得A、B之间的距离与A、C之间的距离相等,并测得BC长为240米,A到BC的距离为5米,如图1所示.请你帮他们求出滴水湖的半径.
【举一反三】
气象台发布的卫星云图显示,代号为W的台风在某海岛(设为点O)的南偏东45°方向的B点生成,测得OB=100√6km.台风中心从点B以40km/h的速度向正北方向移动,经5h后到达海面上的点C处.因受气旋影响,台风中心从点C开始以30km/h的速度向北偏西60°方向继续移动.以O为原点建立如图所示的直角坐标系.
(1)台风生成中心点B的坐标为 ______ ,台风中心转折点C的坐标为 _____ (结果保留根号)
(2)已知距台风中心20km的范围内均会受到台风的侵袭.如果某城市(设为点A)位于点O的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
考点6.借助图形解决代数式或函数最值问题
例10.解关于x的方程
例11.已知,求S的最小值。
【举一反三】
1 解关于x的方程
考点7.借助图形解决函数解析式问题
例12 在同一坐标系内,直线l1:y=(k-2)x+k和l2:y=kx的位置可能为( )
例13.如果一次函数的图象经过第二、三、四象限,那么( )
(A)且 (B)且
(C)且 (D)且
例14.一次函数与,它们在同一坐标系内的大致图象是( )
【举一反三】
1 一次函数y=kx+b的图象经过点(m,1)和(-1,m)其中m>-1则k、b应满足( )
(A)k>0且b>0 (B)k>0且b<0
(C)k<0且b>0 (D)k<0且b<0
2 如果函数y=kx+b的图象在第一、二、三象限内,那么函数y=kx2+bx-1的图象大致是( )
3 当时,反比例函数和一次函数的图象大致是( )
考点8.借助图形解决实际问题
例15.(09年北京)如图,A、B两点在函数的图象上.
(1)求的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数。
【举一反三】
1 某商业公司为指导某种应季商品的生产和销售,对二月份至七月份的该商品的销售和成本进行了调研,结果如下:每件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图),每件商品的成本Q(元)与时间t的关系可用一条抛物线的一部分上的点来表示(如图)(说明:图①、图②中的每一个实心黑点所对应的纵坐标,分别指相应月份的售价和成本)
请你根据图像提供的信息回答:
(1)每件商品在3月份出售时的利润(利润=售价-成本)是多少元?
(2)求图中表示的每件商品的成本Q(元)与时间t(月)之间的函数关系式(不要求写出自变量的取值范围)
(3)你能求出三月份至七月份每件商品的利润W(元)与时间t(月)之间的函数关系式吗?(请写出计算过程,不要求写自变量的取值范围)若该公司共有此种商品30000件,准备在一个月内全部售完,请你计算一下至少可获利多少元?
0
1
A
(第9题图)
(第4题)
y
O
图2
Q(5, 5)
P(2, 3)
y
O
图1
1
1
x
x
t
h
O
t
h
O
t
h
O
h
t
O
图1
A
B
C
30°
45°
3图
·
·
·
A
B
C
例4图2
·
O
D
A
B
C
D
同课章节目录
