1.7.1定积分在几何中的应用-2020-2021学年人教A版高中数学选修2-2课件(16张PPT)
文档属性
| 名称 | 1.7.1定积分在几何中的应用-2020-2021学年人教A版高中数学选修2-2课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 423.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 21:42:39 | ||
图片预览



文档简介
1.7.1定积分在几何中的应用
教学目标:
1.了解定积分的几何意义及微积分的基本定理.
2.掌握利用定积分求曲边图形的面积
教学重点与难点:
1.定积分的概念及几何意义
2.定积分的基本性质及运算的应用
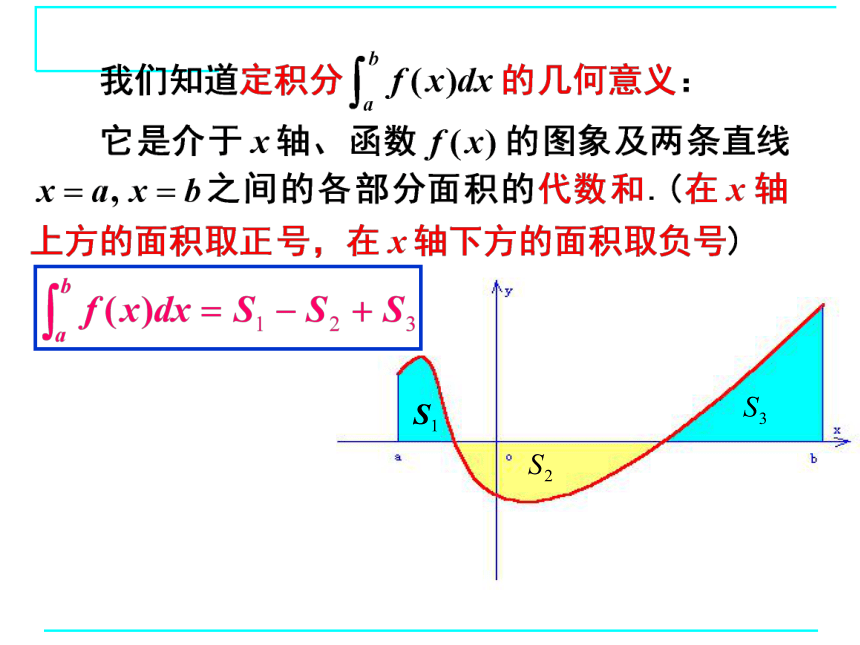
复习
微积分基本定理(牛顿-莱布尼茨公式)
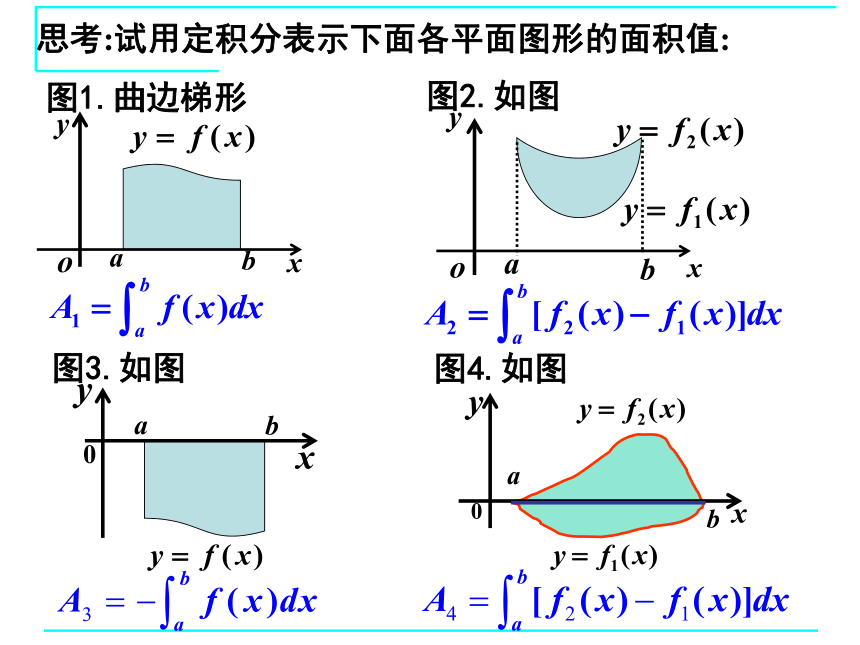
思考:试用定积分表示下面各平面图形的面积值:
图1.曲边梯形
x
y
o
图2.如图
x
y
o
图4.如图
图3.如图
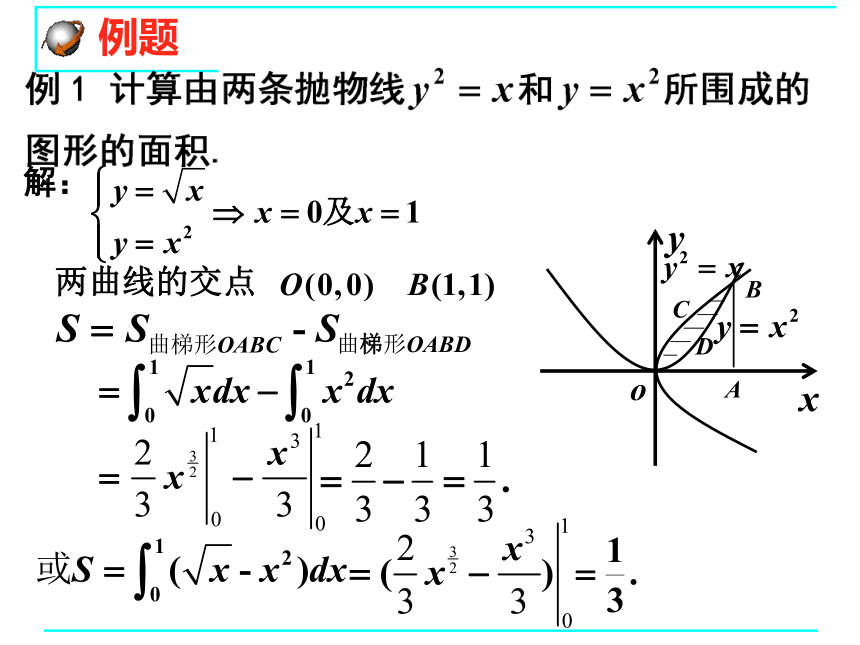
解:
两曲线的交点
o
x
y
例题
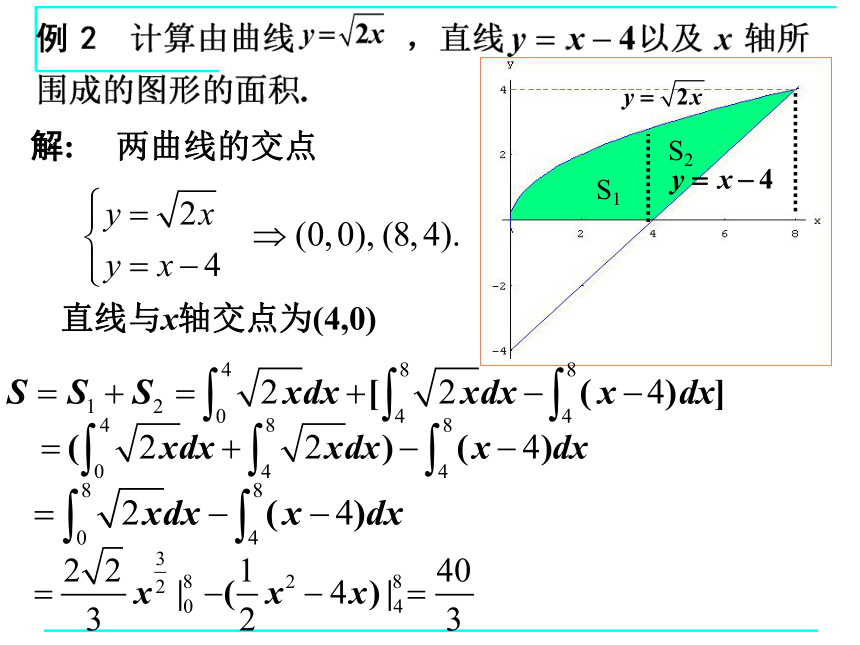
解:
两曲线的交点
直线与x轴交点为(4,0)
S1
S2
解:
两曲线的交点
练习
1.定积分在几何中的应用,主要用于求平面曲边图形的面积.解题时,一般先要画出草图,再
根据图形确定被积函数以及积分的上、下限.
2.定积分只能用于求曲边梯形的面积,对于非规则曲边梯形,一般要将其分割或补形为规则曲边梯形,再利用定积分的和与差求面积.对于分割或补形中的多边形的面积,可直接利用相关面积公式求解.
归纳小结
课堂小结
求在直角坐标系下平面图形的面积步骤:
1. 作图象;
2. 求交点的横坐标,定出积分上、下限;
3. 确定被积函数,用定积分表示所求的面积,特别注意分清被积函数的上、下位置;
4. 用牛顿-莱布尼茨公式求定积分.
解:
两曲线的交点
于是所求面积
说明:注意各积分区间上被积函数的形式.
练习
例3.直线y=kx将抛物线y=x-x2与x轴所围成的平面图形分成面积相等的两部分,求实数k的值2与x轴所围成的平面图形分成面积相等的两部分,求实数k的值
练习3.曲线 与在曲线上某点的切线l及 轴所围成的图形的面积为 ,求切线l的方程.
当堂练习:
1:计算曲线 与直线 y=x+3所围成图形的面积。
2.求曲线 所围成的图形的面积。
3.求由曲线 所围成图形的面积。
变式训练:
(1)计算由曲线 所围成图形的面积。
(2)计算由曲线 所围成的平面图形的面积。
思考题:在区间(0,1]上,给定曲线 ,试在此区间确定t的值,使图中的阴影部分的面积 与 之和最小.
教学目标:
1.了解定积分的几何意义及微积分的基本定理.
2.掌握利用定积分求曲边图形的面积
教学重点与难点:
1.定积分的概念及几何意义
2.定积分的基本性质及运算的应用
复习
微积分基本定理(牛顿-莱布尼茨公式)
思考:试用定积分表示下面各平面图形的面积值:
图1.曲边梯形
x
y
o
图2.如图
x
y
o
图4.如图
图3.如图
解:
两曲线的交点
o
x
y
例题
解:
两曲线的交点
直线与x轴交点为(4,0)
S1
S2
解:
两曲线的交点
练习
1.定积分在几何中的应用,主要用于求平面曲边图形的面积.解题时,一般先要画出草图,再
根据图形确定被积函数以及积分的上、下限.
2.定积分只能用于求曲边梯形的面积,对于非规则曲边梯形,一般要将其分割或补形为规则曲边梯形,再利用定积分的和与差求面积.对于分割或补形中的多边形的面积,可直接利用相关面积公式求解.
归纳小结
课堂小结
求在直角坐标系下平面图形的面积步骤:
1. 作图象;
2. 求交点的横坐标,定出积分上、下限;
3. 确定被积函数,用定积分表示所求的面积,特别注意分清被积函数的上、下位置;
4. 用牛顿-莱布尼茨公式求定积分.
解:
两曲线的交点
于是所求面积
说明:注意各积分区间上被积函数的形式.
练习
例3.直线y=kx将抛物线y=x-x2与x轴所围成的平面图形分成面积相等的两部分,求实数k的值2与x轴所围成的平面图形分成面积相等的两部分,求实数k的值
练习3.曲线 与在曲线上某点的切线l及 轴所围成的图形的面积为 ,求切线l的方程.
当堂练习:
1:计算曲线 与直线 y=x+3所围成图形的面积。
2.求曲线 所围成的图形的面积。
3.求由曲线 所围成图形的面积。
变式训练:
(1)计算由曲线 所围成图形的面积。
(2)计算由曲线 所围成的平面图形的面积。
思考题:在区间(0,1]上,给定曲线 ,试在此区间确定t的值,使图中的阴影部分的面积 与 之和最小.
