2020-2021学年高中数学必修5第一章第一节正弦定理课件(共14张PPT)
文档属性
| 名称 | 2020-2021学年高中数学必修5第一章第一节正弦定理课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 390.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览




文档简介
正弦定理
必修五第一章 解三角形
情境引入
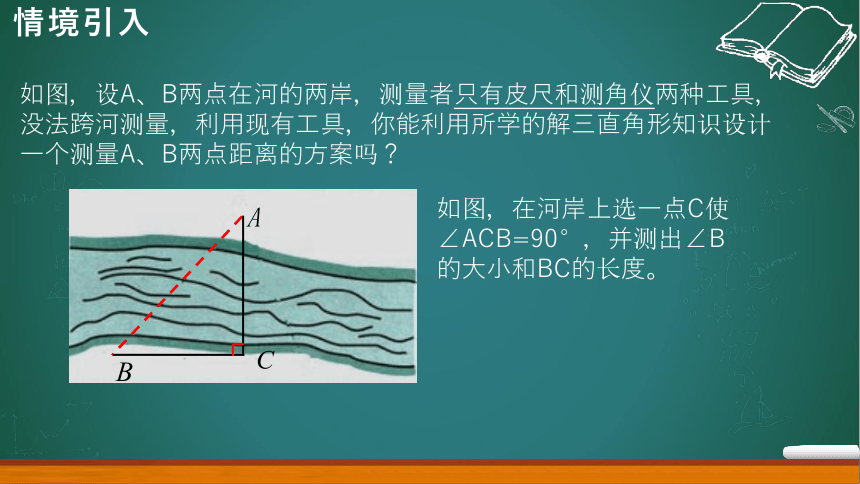
如图,设A、B两点在河的两岸,测量者只有皮尺和测角仪两种工具,没法跨河测量,利用现有工具,你能利用所学的解三直角形知识设计一个测量A、B两点距离的方案吗?
如图,在河岸上选一点C使∠ACB=90°,并测出∠B的大小和BC的长度。
情境引入
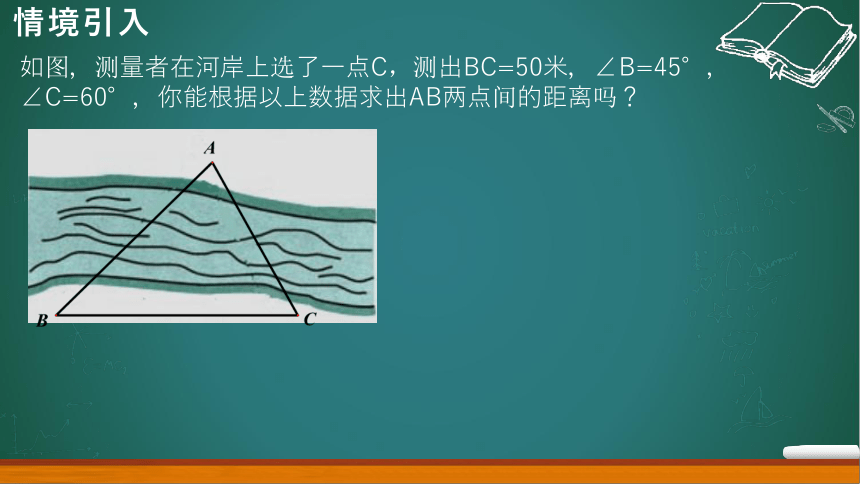
如图,测量者在河岸上选了一点C,测出BC=50米,∠B=45°,∠C=60°,你能根据以上数据求出AB两点间的距离吗?
数学建模
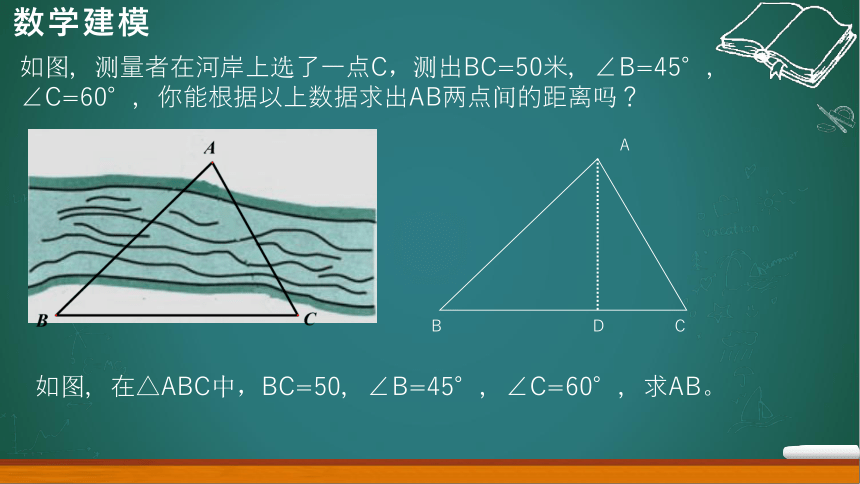
如图,测量者在河岸上选了一点C,测出BC=50米,∠B=45°,∠C=60°,你能根据以上数据求出AB两点间的距离吗?
A
B
C
如图,在△ABC中,BC=50,∠B=45°,∠C=60°,求AB。
D
探究1 直角三角形边角数量关系
在直角△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,探究直角三角形的边角数量关系。
解:根据锐角三角函数(正弦)的定义
探究2 斜三角形的边角关系(验证)
(1)等边△ABC
(2)△ABC中 ∠A=∠B=30° ( )
验证关系式 在下列三角形中成立吗?
探究2 斜三角形的边角关系(猜想)
猜想:在任意斜三角形中也存在下列边角关系。
探究2 斜三角形的边角关系(证明)
如图在锐角△ABC中,设AC=b,BC=a,AB=c
A
B
C
D
探究2 斜三角形的边角关系(证明)
如图在钝角△ABC中,设AC=b,BC=a,AB=c
D
A
B
C
概念生成
正弦定理(law of sines)
在任意一个三角形中,各边和它所对的角的正弦的比相等.
即
学以致用
如图,测量者在河岸上选了一点C,测出BC=54米,∠B=45°,∠C=60°,你能根据以上数据求出AB两点间的距离吗?
A
B
C
如图,在△ABC中,BC=54,∠B=45°,∠C=60°,求AB。
学以致用
1.在△ABC中,a=2,A=30°,B=45°,解三角形。
2.在△ABC中,a=2√2,b=2√3,A=45°,解三角形。
已知两角及其中一角的对边(两角及任意一边)
已知两边及其一边的对角
探究3 已知两边及一边的对角解的情况
2.在△ABC中,a=2√2,b=2√3,A=45°,解三角形。
变式1 在△ABC中,a=√2,b=2√3,A=45°,解三角形。
变式2 在△ABC中,a=2√6,b=2√3,A=45°,解三角形。
解1:B=60°,C=45°,c=√6+√2
解2:B=120°,C=15°,c=√6-√2
两解
无解
B=30°,C=105°,c=√6+3√2
一解
思考:当已知三角形两边及其一边的对角时,什么时候有两解、一解,无解?
探究4 正弦定理其他证明方法
如图圆O是△ABC的外接圆,其半径为R,∠A、∠B、∠C的对边分别为a、b、c。
D
A
B
C
O
必修五第一章 解三角形
情境引入
如图,设A、B两点在河的两岸,测量者只有皮尺和测角仪两种工具,没法跨河测量,利用现有工具,你能利用所学的解三直角形知识设计一个测量A、B两点距离的方案吗?
如图,在河岸上选一点C使∠ACB=90°,并测出∠B的大小和BC的长度。
情境引入
如图,测量者在河岸上选了一点C,测出BC=50米,∠B=45°,∠C=60°,你能根据以上数据求出AB两点间的距离吗?
数学建模
如图,测量者在河岸上选了一点C,测出BC=50米,∠B=45°,∠C=60°,你能根据以上数据求出AB两点间的距离吗?
A
B
C
如图,在△ABC中,BC=50,∠B=45°,∠C=60°,求AB。
D
探究1 直角三角形边角数量关系
在直角△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,探究直角三角形的边角数量关系。
解:根据锐角三角函数(正弦)的定义
探究2 斜三角形的边角关系(验证)
(1)等边△ABC
(2)△ABC中 ∠A=∠B=30° ( )
验证关系式 在下列三角形中成立吗?
探究2 斜三角形的边角关系(猜想)
猜想:在任意斜三角形中也存在下列边角关系。
探究2 斜三角形的边角关系(证明)
如图在锐角△ABC中,设AC=b,BC=a,AB=c
A
B
C
D
探究2 斜三角形的边角关系(证明)
如图在钝角△ABC中,设AC=b,BC=a,AB=c
D
A
B
C
概念生成
正弦定理(law of sines)
在任意一个三角形中,各边和它所对的角的正弦的比相等.
即
学以致用
如图,测量者在河岸上选了一点C,测出BC=54米,∠B=45°,∠C=60°,你能根据以上数据求出AB两点间的距离吗?
A
B
C
如图,在△ABC中,BC=54,∠B=45°,∠C=60°,求AB。
学以致用
1.在△ABC中,a=2,A=30°,B=45°,解三角形。
2.在△ABC中,a=2√2,b=2√3,A=45°,解三角形。
已知两角及其中一角的对边(两角及任意一边)
已知两边及其一边的对角
探究3 已知两边及一边的对角解的情况
2.在△ABC中,a=2√2,b=2√3,A=45°,解三角形。
变式1 在△ABC中,a=√2,b=2√3,A=45°,解三角形。
变式2 在△ABC中,a=2√6,b=2√3,A=45°,解三角形。
解1:B=60°,C=45°,c=√6+√2
解2:B=120°,C=15°,c=√6-√2
两解
无解
B=30°,C=105°,c=√6+3√2
一解
思考:当已知三角形两边及其一边的对角时,什么时候有两解、一解,无解?
探究4 正弦定理其他证明方法
如图圆O是△ABC的外接圆,其半径为R,∠A、∠B、∠C的对边分别为a、b、c。
D
A
B
C
O
