2020-2021学年高一下学期数学人教A版(2019)必修第二册第八章8.4空间点、直线、平面的平行同步习题
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版(2019)必修第二册第八章8.4空间点、直线、平面的平行同步习题 |  | |
| 格式 | doc | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 05:53:31 | ||
图片预览



文档简介
2020-2021学年必修第二册数学高一下第八章8.4空间直线、平面的平行同步习题
一、单选题
1.如图所示,在长方体AC1中,E,F分别是B1O和C1O的中点,则长方体的各棱中与EF平行的有( )
A.3条 B.4条
C.5条 D.6条
2.平面与平面平行的条件可以是( )
A.内有无穷多条直线与平行
B.内的任何直线都与平行
C.直线在平面内,直线在平面内,且,
D.直线,直线
3.如图所示,在三棱锥中,、、、分别为、、、上的点,,则与( )
A.平行 B.相交 C.异面 D.以上皆有可能
4.若直线a平面α,A?α,且直线a与点A位于α的两侧,B,C∈a,AB,AC分别交平面α于点E,F,若BC=4,CF=5,AF=3,则EF的值为( )
A.3 B. C. D.
5.如图所示,四边形EFGH为四面体ABCD的一个截面,若,则与平面EFGH平行的直线有( )
A.0条 B.1条 C.2条 D.3条
6.如图,在三棱锥中,,分别为AB,AD的中点,过EF的平面截三棱锥得到的截面为EFHG.则下列结论中不一定成立的是( )
A. B.
C.平面 D.平面
7.已知是三条不同的直线,是三个不同的平面,有下列命题:
①
②若则
③则
④直线,直线,那么
⑤若,则
⑥若,则,
其中所有正确命题数( )
A. B. C. D.
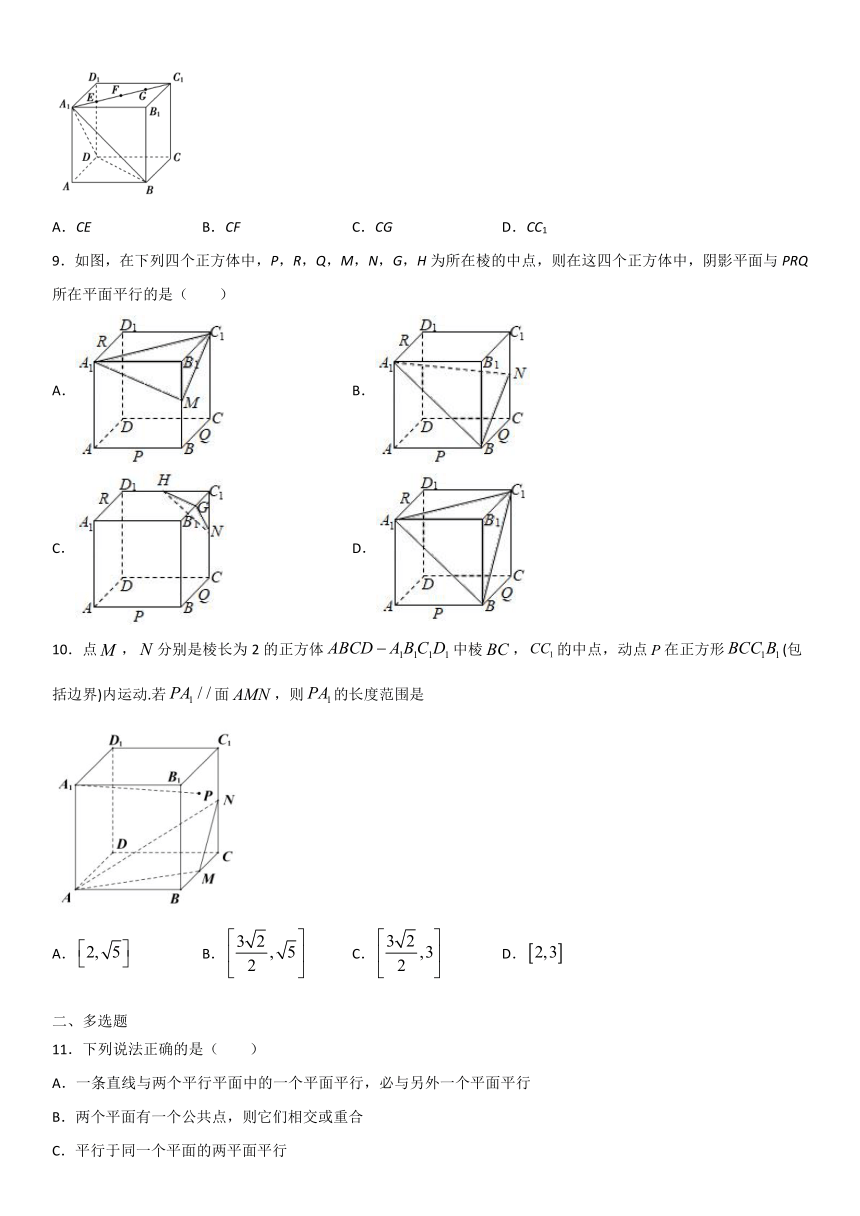
8.如图,在正方体ABCD-A1B1C1D1中,已知E,F,G分别是线段A1C1上的点,且A1E=EF=FG=GC1.则下列直线与平面A1BD平行的是( )
A.CE B.CF C.CG D.CC1
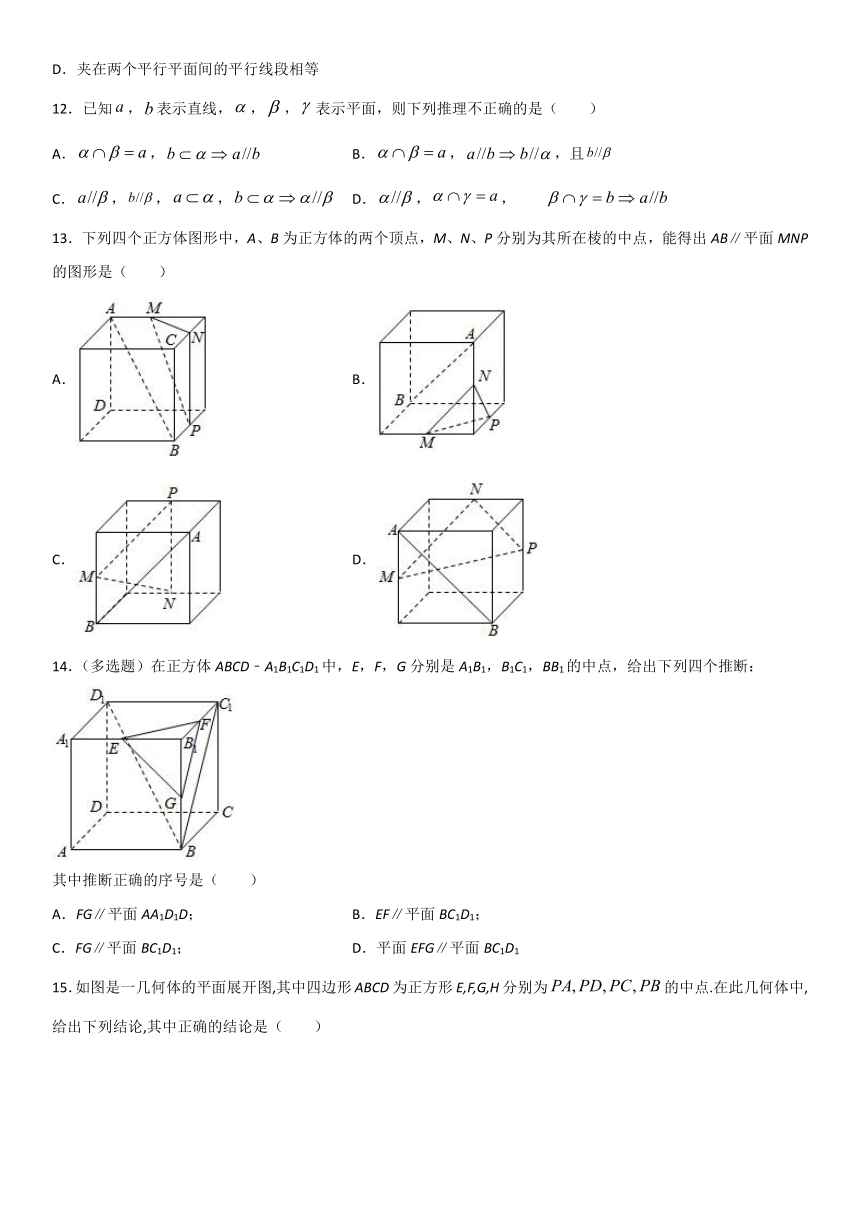
9.如图,在下列四个正方体中,P,R,Q,M,N,G,H为所在棱的中点,则在这四个正方体中,阴影平面与PRQ所在平面平行的是( )
A. B.
C. D.
10.点,分别是棱长为2的正方体中棱,的中点,动点在正方形(包括边界)内运动.若面,则的长度范围是
A. B. C. D.
二、多选题
11.下列说法正确的是( )
A.一条直线与两个平行平面中的一个平面平行,必与另外一个平面平行
B.两个平面有一个公共点,则它们相交或重合
C.平行于同一个平面的两平面平行
D.夹在两个平行平面间的平行线段相等
12.已知,表示直线,,,表示平面,则下列推理不正确的是( )
A., B.,,且
C.,,, D.,,
13.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )
A. B.
C. D.
14.(多选题)在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
其中推断正确的序号是( )
A.FG∥平面AA1D1D; B.EF∥平面BC1D1;
C.FG∥平面BC1D1; D.平面EFG∥平面BC1D1
15.如图是一几何体的平面展开图,其中四边形ABCD为正方形E,F,G,H分别为的中点.在此几何体中,给出下列结论,其中正确的结论是( )
A.平面平面 B.直线平面
C.直线平面 D.直线平面
三、填空题
16.在直三棱柱ABC﹣A1B1C1中,D为AA1中点,点P在侧面BCC1B1上运动,当点P满足条件___________时,A1P平面BCD(答案不唯一,填一个满足题意的条件即可)
17.如图,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS是平行直线的图是________(填序号).
18.下列条件中,能判定平面与平面平行的条件可以是___________.(写出所有正确条件的序号)
①内有无穷多条直线都与平行;
②内的任何一条直线都与平行;
③直线,直线,且,;
④,,.
19.如图,在四棱锥中,底面为平行四边形,为的中点,为的中点,则与平面的关系是________.
20.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
四、解答题
21.如图,在三棱柱中,,,,分别是,,,的中点,求证:
(1),,,四点共面;
(2)平面平面.
22.如图所示,已知是所在平面外一点,,分别是,的中点.
(1)求证:平面;
(2)设平面平面,求证:.
23.如图,在多面体ABCDEF中,ABCD是正方形,AB=2,DE=BF=4,BFDE,M为棱AE的中点.求证:平面BMD平面EFC.
24.如图,在三棱柱中,侧棱底面,,为的中点,,.求证:平面;
25.如图,在三棱柱中,侧棱底面,,为的中点,,.
(1)求证:平面;
(2)求三棱锥的体积.
26.如图所示,在直三棱柱中,,,是的中点.
(Ⅰ)求证:直线平面;
(Ⅱ)设为线段上的动点,求三棱锥的体积.
参考答案
1.B
由于E,F分别是B1O,C1O的中点,故EF∥B1C1,
因为与棱B1C1平行的棱还有3条:AD, BC,A1D1,所以共有4条.
2.B
若内有无穷多条直线与平行,则平面与平面相交或平行,故不正确;
若内的任何直线都与平行,则,故B正确;
若直线在平面内,直线在平面内,且,,则平面与平面相交或平行,故C不正确;
若直线,直线,则平面与平面相交或平行,故D不正确.
3.A
,平面,平面,平面,
平面,平面平面,因此,.
故选:A.
4.B
解:∵BC∥α,且平面ABC∩α=EF,
∴EF∥BC,∴=,即=.
∴EF=.
5.C
∵,∴EF//AB.
又EF?平面EFGH,AB?平面EFGH,
∴AB//平面EFGH.
同理,由,
可证CD//平面EFGH.
∴与平面EFGH平行的直线有2条.
6.D
对于,,分别为,的中点,,EF与平面BCD平行
过的平面截三棱锥得到的截面为,平面平面,
,,故AB正确;
对于,,平面,平面,平面,故正确;
对于,的位置不确定,与平面有可能相交,故错误.
故选:D.
7.B
对于①:根据平行的性质有,故①正确;
对于②:由得或相交,故②不正确;
对于③:由得,或异面,故③不正确;
对于④:由直线,直线,可得,异面,相交,故④不正确;
对于⑤:由,得或相交,故⑤不正确;
对于⑥:若,由面面平行的传递性得,故⑥正确,
所以正确的命题有①⑥,
8.B
如图,连接AC,使AC交BD于点O,连接A1O,CF,
在正方体ABCD?-A1B1C1D1中,由于,
又OC=AC,可得:,即四边形A1OCF为平行四边形,
可得:A1O∥CF,又A1O?平面A1BD,CF?平面A1BD,
可得CF∥平面A1BD,
9.D
由题意可知经过P、Q、R三点的平面即为平面,如下图所示:
对选项:可知N在经过P、Q、R三点的平面上,所以B、C错误;
对:MC1与是相交直线,所以A不正确;
对:因为//,,//,
又容易知也相交,
平面;平面,
故平面//平面
10.B
取,中点,, 连接、 .
则∥.∥.又因为 .
所以平面∥平面.
又因为动点在正方形(包括边界)内运动,
所以点的轨迹为线段.
又因为正方体的棱长为2,
所以, .
所以为等腰三角形.
故当点在点或者在点处时,此时最大,最大值为.
当点为中点时,最小,最小值为 .
故选:B.
11.BCD
对于A选项,一条直线与两个平行平面中的一个平面平行,
则该直线与另外一个平面平行或该直线在另外一个平面内,A选项错误;
对于B选项,两个平面有一个公共点,则它们相交或重合,B选项正确;
对于C选项,由面面平行的性质可知,平行于同一个平面的两平面平行,C选项正确;
对于D选项,如下图所示:
已知平面平面,、,、,,
那么直线、可确定平面,
,,,,则四边形为平行四边形,
所以,,D选项正确.
故选:BCD.
12.ABC
A. 因为,,则平行或相交,故错误;
B. 因为,,则或 ,或 ,故错误;
C. 因为,,,,则平行或相交,故错误;
D. 因为,,,由面面平行的性质定理得 ,故正确;
13.AD
解:在A中,连接AC,则AC∥MN,由正方体性质得到平面MNP∥平面ABC,
∴AB∥平面MNP,故A成立;
对于B,若下底面中心为O,则NO∥AB,NO∩面MNP=N,
∴AB与面MNP不平行,故B不成立;
对于C,过M作ME∥AB,则E是中点,
则ME与平面PMN相交,则AB与平面MNP相交,
∴AB与面MNP不平行,故C不成立;
对于D,连接CE,则AB∥CE,NP∥CD,则AB∥PN,∴AB∥平面MNP,故D成立.
故选:AD.
14.AC
解:在正方体中,,,分别是,,的中点,
,,,
平面,平面,平面,故A正确;
,与平面相交,与平面相交,故B错误;
,,分别是,,的中点,
,平面,平面,
平面,故C正确;
与平面相交,平面与平面相交,故D错误.
故选:AC.
15.ABC
作出立体图形如图所示.连接四点构成平面.
对于A,因为E,F分别是的中点,所以.又平面,平面,所以平面.同理, 平面.又,平面,平面,所以平面平面,故A正确;
对于B,连接,设的中点为M,则M也是的中点,所以,又平面,平面,所以平面,故B正确;
对于C,由A中的分析知,,所以,因为平面,平面,所以直线平面,故C正确;
对于,根据C中的分析可知再结合图形可得,,则直线与平面不平行,故D错误.
16.P是CC1中点
取CC1中点P,连结A1P,
∵在直三棱柱ABC﹣A1B1C1中,D为AA1中点,点P在侧面BCC1B1上运动,
∴当点P满足条件P是CC1中点时,A1PCD,
∵A1P?平面BCD,CD?平面BCD,
∴当点P满足条件P是CC1中点时,A1P平面BCD
17.①②
根据正方体的结构特征,可得①②中RS与PQ均是平行直线,④中RS和PQ是相交直线,③中RS和PQ是是异面直线.
故答案为:①②.
18.②④
当内有无穷多条直线都与平行,平面与平面可能平行,也可能相交,故①不正确.
当内的任何一条直线都与平行时,则平面内必有2条相交直线和平面平行,据面面平行的判定定理,平面与平面平行,故②正确.
当直线,直线,且,时,平面与平面可能平行,也可能相交,故③不正确.
当,,时,可证,这样,平面与平面都和直线垂直,故平面与平面平行,故④正确.
综上,②④正确,①③错误,
19.平行
取的中点,连接.
分别为中点,,
又四边形为平行四边形,为中点,,
,四边形为平行四边形,,
又平面,平面,平面.
故答案为:平行.
20.
∵MN//平面ABCD,平面PMNQ∩平面ABCD=PQ,MN?平面PQNM,
∴MN//PQ,易知DP=DQ=,
故PQ=.
故答案为:
21.
证明:(1)?分别为,中点,,
三棱柱中,,
???四点共面;
(2)?分别为?中点,,,
又不在平面BCHG中,平面 BCHG,所以平面BCHG
又?分别为三棱柱侧面平行四边形对边?中点,
四边形为平行四边形,,又不在平面BCHG,平面BCHG
平面中有两条直线?分别与平面平行
平面平面.
22.
证明:(1)如图,取的中点,连接,,
可以证得且,
所以四边形是平行四边形,所以.
又平面,平面,所以平面.
(2)因为,平面,平面,所以平面.
又因为平面平面,所以.
23
证明:如图,连接AC,交BD于点N,
∴N为AC的中点,连接MN,则MNEC.
∵面EFC,面EFC,
∴MN平面EFC.
∵BFDE,BF=DE,
∴四边形BDEF为平行四边形,
∴BDEF.
∵平面EFC,平面EFC,
∴BD平面EFC,又MN∩BD=N,
∴平面BMD平面EFC.
24.
如图所示:
连接与交于点O,连接OD,
因为O,D为中点,
所以,
又平面,平面,
所以平面.
25.
(1)如图所示:
连接与交于点O,连接OD,
因为O,D为中点,
所以,
又平面,平面,
所以平面;
(2)因为侧棱底面,
所以,即,
又,,
所以平面,
因为为的中点,
所以点D到平面的距离为1,
又,
所以.
26.
解:(Ⅰ)连接交于,连接,
∵四边形为正方形,∴为的中点,
又是的中点,∴在中,,
又平面,平面,
∴直线平面.
(Ⅱ)∵平面,∴,
∴,∴.
一、单选题
1.如图所示,在长方体AC1中,E,F分别是B1O和C1O的中点,则长方体的各棱中与EF平行的有( )
A.3条 B.4条
C.5条 D.6条
2.平面与平面平行的条件可以是( )
A.内有无穷多条直线与平行
B.内的任何直线都与平行
C.直线在平面内,直线在平面内,且,
D.直线,直线
3.如图所示,在三棱锥中,、、、分别为、、、上的点,,则与( )
A.平行 B.相交 C.异面 D.以上皆有可能
4.若直线a平面α,A?α,且直线a与点A位于α的两侧,B,C∈a,AB,AC分别交平面α于点E,F,若BC=4,CF=5,AF=3,则EF的值为( )
A.3 B. C. D.
5.如图所示,四边形EFGH为四面体ABCD的一个截面,若,则与平面EFGH平行的直线有( )
A.0条 B.1条 C.2条 D.3条
6.如图,在三棱锥中,,分别为AB,AD的中点,过EF的平面截三棱锥得到的截面为EFHG.则下列结论中不一定成立的是( )
A. B.
C.平面 D.平面
7.已知是三条不同的直线,是三个不同的平面,有下列命题:
①
②若则
③则
④直线,直线,那么
⑤若,则
⑥若,则,
其中所有正确命题数( )
A. B. C. D.
8.如图,在正方体ABCD-A1B1C1D1中,已知E,F,G分别是线段A1C1上的点,且A1E=EF=FG=GC1.则下列直线与平面A1BD平行的是( )
A.CE B.CF C.CG D.CC1
9.如图,在下列四个正方体中,P,R,Q,M,N,G,H为所在棱的中点,则在这四个正方体中,阴影平面与PRQ所在平面平行的是( )
A. B.
C. D.
10.点,分别是棱长为2的正方体中棱,的中点,动点在正方形(包括边界)内运动.若面,则的长度范围是
A. B. C. D.
二、多选题
11.下列说法正确的是( )
A.一条直线与两个平行平面中的一个平面平行,必与另外一个平面平行
B.两个平面有一个公共点,则它们相交或重合
C.平行于同一个平面的两平面平行
D.夹在两个平行平面间的平行线段相等
12.已知,表示直线,,,表示平面,则下列推理不正确的是( )
A., B.,,且
C.,,, D.,,
13.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )
A. B.
C. D.
14.(多选题)在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
其中推断正确的序号是( )
A.FG∥平面AA1D1D; B.EF∥平面BC1D1;
C.FG∥平面BC1D1; D.平面EFG∥平面BC1D1
15.如图是一几何体的平面展开图,其中四边形ABCD为正方形E,F,G,H分别为的中点.在此几何体中,给出下列结论,其中正确的结论是( )
A.平面平面 B.直线平面
C.直线平面 D.直线平面
三、填空题
16.在直三棱柱ABC﹣A1B1C1中,D为AA1中点,点P在侧面BCC1B1上运动,当点P满足条件___________时,A1P平面BCD(答案不唯一,填一个满足题意的条件即可)
17.如图,点P,Q,R,S分别在正方体的四条棱上,且是所在棱的中点,则直线PQ与RS是平行直线的图是________(填序号).
18.下列条件中,能判定平面与平面平行的条件可以是___________.(写出所有正确条件的序号)
①内有无穷多条直线都与平行;
②内的任何一条直线都与平行;
③直线,直线,且,;
④,,.
19.如图,在四棱锥中,底面为平行四边形,为的中点,为的中点,则与平面的关系是________.
20.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
四、解答题
21.如图,在三棱柱中,,,,分别是,,,的中点,求证:
(1),,,四点共面;
(2)平面平面.
22.如图所示,已知是所在平面外一点,,分别是,的中点.
(1)求证:平面;
(2)设平面平面,求证:.
23.如图,在多面体ABCDEF中,ABCD是正方形,AB=2,DE=BF=4,BFDE,M为棱AE的中点.求证:平面BMD平面EFC.
24.如图,在三棱柱中,侧棱底面,,为的中点,,.求证:平面;
25.如图,在三棱柱中,侧棱底面,,为的中点,,.
(1)求证:平面;
(2)求三棱锥的体积.
26.如图所示,在直三棱柱中,,,是的中点.
(Ⅰ)求证:直线平面;
(Ⅱ)设为线段上的动点,求三棱锥的体积.
参考答案
1.B
由于E,F分别是B1O,C1O的中点,故EF∥B1C1,
因为与棱B1C1平行的棱还有3条:AD, BC,A1D1,所以共有4条.
2.B
若内有无穷多条直线与平行,则平面与平面相交或平行,故不正确;
若内的任何直线都与平行,则,故B正确;
若直线在平面内,直线在平面内,且,,则平面与平面相交或平行,故C不正确;
若直线,直线,则平面与平面相交或平行,故D不正确.
3.A
,平面,平面,平面,
平面,平面平面,因此,.
故选:A.
4.B
解:∵BC∥α,且平面ABC∩α=EF,
∴EF∥BC,∴=,即=.
∴EF=.
5.C
∵,∴EF//AB.
又EF?平面EFGH,AB?平面EFGH,
∴AB//平面EFGH.
同理,由,
可证CD//平面EFGH.
∴与平面EFGH平行的直线有2条.
6.D
对于,,分别为,的中点,,EF与平面BCD平行
过的平面截三棱锥得到的截面为,平面平面,
,,故AB正确;
对于,,平面,平面,平面,故正确;
对于,的位置不确定,与平面有可能相交,故错误.
故选:D.
7.B
对于①:根据平行的性质有,故①正确;
对于②:由得或相交,故②不正确;
对于③:由得,或异面,故③不正确;
对于④:由直线,直线,可得,异面,相交,故④不正确;
对于⑤:由,得或相交,故⑤不正确;
对于⑥:若,由面面平行的传递性得,故⑥正确,
所以正确的命题有①⑥,
8.B
如图,连接AC,使AC交BD于点O,连接A1O,CF,
在正方体ABCD?-A1B1C1D1中,由于,
又OC=AC,可得:,即四边形A1OCF为平行四边形,
可得:A1O∥CF,又A1O?平面A1BD,CF?平面A1BD,
可得CF∥平面A1BD,
9.D
由题意可知经过P、Q、R三点的平面即为平面,如下图所示:
对选项:可知N在经过P、Q、R三点的平面上,所以B、C错误;
对:MC1与是相交直线,所以A不正确;
对:因为//,,//,
又容易知也相交,
平面;平面,
故平面//平面
10.B
取,中点,, 连接、 .
则∥.∥.又因为 .
所以平面∥平面.
又因为动点在正方形(包括边界)内运动,
所以点的轨迹为线段.
又因为正方体的棱长为2,
所以, .
所以为等腰三角形.
故当点在点或者在点处时,此时最大,最大值为.
当点为中点时,最小,最小值为 .
故选:B.
11.BCD
对于A选项,一条直线与两个平行平面中的一个平面平行,
则该直线与另外一个平面平行或该直线在另外一个平面内,A选项错误;
对于B选项,两个平面有一个公共点,则它们相交或重合,B选项正确;
对于C选项,由面面平行的性质可知,平行于同一个平面的两平面平行,C选项正确;
对于D选项,如下图所示:
已知平面平面,、,、,,
那么直线、可确定平面,
,,,,则四边形为平行四边形,
所以,,D选项正确.
故选:BCD.
12.ABC
A. 因为,,则平行或相交,故错误;
B. 因为,,则或 ,或 ,故错误;
C. 因为,,,,则平行或相交,故错误;
D. 因为,,,由面面平行的性质定理得 ,故正确;
13.AD
解:在A中,连接AC,则AC∥MN,由正方体性质得到平面MNP∥平面ABC,
∴AB∥平面MNP,故A成立;
对于B,若下底面中心为O,则NO∥AB,NO∩面MNP=N,
∴AB与面MNP不平行,故B不成立;
对于C,过M作ME∥AB,则E是中点,
则ME与平面PMN相交,则AB与平面MNP相交,
∴AB与面MNP不平行,故C不成立;
对于D,连接CE,则AB∥CE,NP∥CD,则AB∥PN,∴AB∥平面MNP,故D成立.
故选:AD.
14.AC
解:在正方体中,,,分别是,,的中点,
,,,
平面,平面,平面,故A正确;
,与平面相交,与平面相交,故B错误;
,,分别是,,的中点,
,平面,平面,
平面,故C正确;
与平面相交,平面与平面相交,故D错误.
故选:AC.
15.ABC
作出立体图形如图所示.连接四点构成平面.
对于A,因为E,F分别是的中点,所以.又平面,平面,所以平面.同理, 平面.又,平面,平面,所以平面平面,故A正确;
对于B,连接,设的中点为M,则M也是的中点,所以,又平面,平面,所以平面,故B正确;
对于C,由A中的分析知,,所以,因为平面,平面,所以直线平面,故C正确;
对于,根据C中的分析可知再结合图形可得,,则直线与平面不平行,故D错误.
16.P是CC1中点
取CC1中点P,连结A1P,
∵在直三棱柱ABC﹣A1B1C1中,D为AA1中点,点P在侧面BCC1B1上运动,
∴当点P满足条件P是CC1中点时,A1PCD,
∵A1P?平面BCD,CD?平面BCD,
∴当点P满足条件P是CC1中点时,A1P平面BCD
17.①②
根据正方体的结构特征,可得①②中RS与PQ均是平行直线,④中RS和PQ是相交直线,③中RS和PQ是是异面直线.
故答案为:①②.
18.②④
当内有无穷多条直线都与平行,平面与平面可能平行,也可能相交,故①不正确.
当内的任何一条直线都与平行时,则平面内必有2条相交直线和平面平行,据面面平行的判定定理,平面与平面平行,故②正确.
当直线,直线,且,时,平面与平面可能平行,也可能相交,故③不正确.
当,,时,可证,这样,平面与平面都和直线垂直,故平面与平面平行,故④正确.
综上,②④正确,①③错误,
19.平行
取的中点,连接.
分别为中点,,
又四边形为平行四边形,为中点,,
,四边形为平行四边形,,
又平面,平面,平面.
故答案为:平行.
20.
∵MN//平面ABCD,平面PMNQ∩平面ABCD=PQ,MN?平面PQNM,
∴MN//PQ,易知DP=DQ=,
故PQ=.
故答案为:
21.
证明:(1)?分别为,中点,,
三棱柱中,,
???四点共面;
(2)?分别为?中点,,,
又不在平面BCHG中,平面 BCHG,所以平面BCHG
又?分别为三棱柱侧面平行四边形对边?中点,
四边形为平行四边形,,又不在平面BCHG,平面BCHG
平面中有两条直线?分别与平面平行
平面平面.
22.
证明:(1)如图,取的中点,连接,,
可以证得且,
所以四边形是平行四边形,所以.
又平面,平面,所以平面.
(2)因为,平面,平面,所以平面.
又因为平面平面,所以.
23
证明:如图,连接AC,交BD于点N,
∴N为AC的中点,连接MN,则MNEC.
∵面EFC,面EFC,
∴MN平面EFC.
∵BFDE,BF=DE,
∴四边形BDEF为平行四边形,
∴BDEF.
∵平面EFC,平面EFC,
∴BD平面EFC,又MN∩BD=N,
∴平面BMD平面EFC.
24.
如图所示:
连接与交于点O,连接OD,
因为O,D为中点,
所以,
又平面,平面,
所以平面.
25.
(1)如图所示:
连接与交于点O,连接OD,
因为O,D为中点,
所以,
又平面,平面,
所以平面;
(2)因为侧棱底面,
所以,即,
又,,
所以平面,
因为为的中点,
所以点D到平面的距离为1,
又,
所以.
26.
解:(Ⅰ)连接交于,连接,
∵四边形为正方形,∴为的中点,
又是的中点,∴在中,,
又平面,平面,
∴直线平面.
(Ⅱ)∵平面,∴,
∴,∴.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
