7.1 行星的运动(基础达标)检测— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册(word含解析)
文档属性
| 名称 | 7.1 行星的运动(基础达标)检测— 2020-2021学年【新教材】人教版(2019)高中物理必修第二册(word含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 360.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览




文档简介
第七章万有引力与宇宙航行第一节行星的运动基础达标(含解析)
一、单选题
1.两颗人造卫星绕地球匀速圆周运动,周期之比是
,则轨道半径之比是( )
A.轨道半径之比是 B.轨道半径之比是
C.轨道半径之比是 D.轨道半径之比是
2.许多科学家在物理学的发展过程中做出了重要贡献,下列叙述错误的是( )
A.开普勒首先指出了行星绕太阳运动的轨道不是圆,而是椭圆
B.海王星是人们根据万有引力定律计算出其轨道后才发现的,被称为“笔尖下发现的行星”
C.开普勒总结出了行星运动的规律,并发现了万有引力定律
D.卡文迪什第一次在实验室里测出了万有引力常量G,被称为“第一个称出地球质量的人”
3.某行星绕太阳运动的椭圆轨道如图所示,和是椭圆轨道的两个焦点,行星在点的速率比在点的速率大,则太阳位于( )
A.位置 B.位置 C.位置 D.位置
4.在“金星凌日”的精彩天象中,观察到太阳表面上有颗小黑点缓慢走过,持续时间达六个半小时,那便是金星,如图所示。下面说法正确的是( )
A.观测“金星凌日”时可将太阳看成质点
B.地球在金星与太阳之间
C.金星绕太阳公转一周时间小于365天
D.相同时间内,金星与太阳连线扫过的面积等于地球与太阳连线扫过的面积
5.关于,,这三个等式的描述正确的是( )
A.不能在实验室验证
B.不能在实验室验证
C.可以在实验室验证
D.是开普勒用第谷观测数据计算推理得出的
6.如图所示是行星m绕太阳M运行情况的示意图,A点是远日点,B点是近日点,CD是椭圆轨道的短轴,下列说法中正确的是( )
A.行星运动到A点时速度最大
B.行星运动到C点或D点时速度最小
C.行星从C点顺时针运动到B点的过程中做加速运动
D.行星从B点顺时针运动到D点的时间与从A点顺时针运动到C点的时间相等
7.地球位于火星与太阳之间且三者在同一直线上时称为“火星冲日”。已知地球绕太阳做圆周运动的周期为T,火星绕太阳做圆周运动的轨道半径为地球绕太阳做圆周运动的轨道半径的n倍。则相邻两次“火星冲日”的时间差为( )
A. B. C. D.
8.某行星和地球绕太阳公转的轨道均可视为圆。每过N年,该行星会运行到日地连线的延长线上,如图所示该行星与地球的公转半径之比为( )
A. B. C. D.
9.阋神星是一个已知的第二大属于柯伊伯带及海王星外天体的矮行星,根据早期观测数据估算,阋神星比冥王星大,在公布其发现时曾被其发现者和等组织称为“第十大行星”。若将地球和阋神星绕太阳的运动看作匀速圆周运动,它们的运行轨道如图所示。已知阋神星绕太阳运行一周的时间约为557年,设地球绕太阳运行的轨道半径为R,则阋神星绕太阳运行的轨道半径约为( )
A. B. C. D.
10.2020年7月23日,我国首个火星探测器“天问一号”由长征五号运载火箭在海南文昌航天发射场成功发射。升空后,它将经历7个月左右的长途跋涉靠近火星,开展火星环绕、表面降落、巡视探测三大任务。假设环绕器绕火星运行的轨道半径约为火星同步卫星轨道半径的,火星自转周期与地球接近,那么环绕器绕火星一圈需要的时间最接近( )
A.1小时 B.3小时 C.6小时 D.12小时
11.中国北斗卫星导航系统已经组网完成,具备区域导航、定位和授时能力,定位精度为分米、厘米级别,测速精度为0.2米/秒,授时精度为10纳秒。北斗导航在轨工作的33颗卫星轨道半径有两种,一种是轨道半径为42000公里的同步地球轨道,另一种是轨道半径为28000公里的中圆地球轨道,则在中圆地球轨道上运行的卫星的周期约为( )
A.5小时 B.13小时 C.16小时 D.44小时
12.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点。已知行星在A点的速率大于在B点的速率,则太阳位于( )
A.F1点 B.F2点 C.O点 D.无法确定
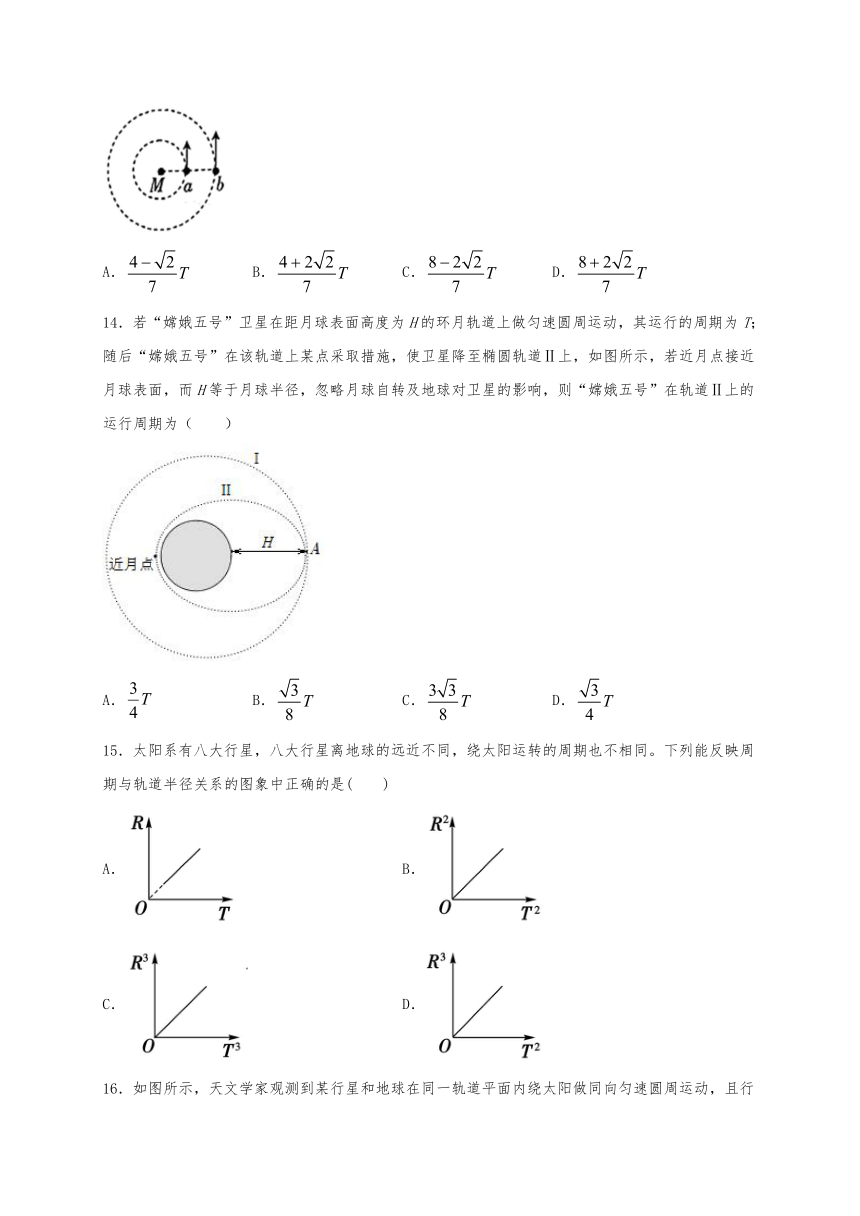
13.如图所示,、两颗行星绕恒星做圆周运动,旋转方向相同,已知行星的轨道半径为行星的2倍,行星的周期为。不考虑、间的万有引力,则、两颗行星连续两次相距最近的时间间隔为( )
A. B. C. D.
14.若“嫦娥五号”卫星在距月球表面高度为H的环月轨道上做匀速圆周运动,其运行的周期为T;随后“嫦娥五号”在该轨道上某点采取措施,使卫星降至椭圆轨道Ⅱ上,如图所示,若近月点接近月球表面,而H等于月球半径,忽略月球自转及地球对卫星的影响,则“嫦娥五号”在轨道Ⅱ上的运行周期为( )
A. B. C. D.
15.太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同。下列能反映周期与轨道半径关系的图象中正确的是( )
A. B.
C. D.
16.如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角。当行星处于最大观察视角处时,是地球上的天文爱好者观察该行星的最佳时期,已知该行星的最大观察视角为θ,不计行星与地球之间的引力,则该行星环绕太阳运动的周期约为( )
A. 年 B.年 C.年 D.年
二、解答题
17.我国航天第一人杨利伟乘坐“神舟”五号载人飞船,在绕地球飞行了14圈、历时21小时后返回地面。已知地球半径R地=6.4×103km,“静止”在赤道上空的卫星的高度为5.67R地,则“神舟”五号离地多高?
18.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷曾经在1662年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定时间就会再次出现。
(1)若这颗彗星在近日点的线速度为v1,在远日点的线速度为v2,则哪个线速度大?
(2)这颗彗星最近出现的时间是1986年,它下次飞近地球大约是哪一年?
19.1970年4月24日,我国发射了第一颗人造卫星,其近地点高度是km,远地点高度是km,设近地点处卫星的速率v1,远地点处卫星速率v2,则v1:v2为多少?(已知km)
参考答案
1.D
【解析】
根据开普勒第三定律
可得
所以
故选D。
2.C
【解析】
A.开普勒首先指出了行星绕太阳运动的轨道不是圆,而是椭圆,A正确;
B.海王星是人们根据万有引力定律计算出其轨道后才发现的,被称为“笔尖下发现的行星”,B正确。
C.万有引力定律是牛顿发现的,C错误;
D.卡文迪什第一次在实验室里测出了万有引力常量G,被称为“第一个称出地球质量的人”,D正确。
故错误的选C。
3.A
【解析】
根据开普勒第二定律,对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积,如果时间间隔相等,那么面积A=面积B,由此可知
所以A点为近日点,B点为远日点,则太阳是位于F2。
故选A。
4.C
【解析】
A.观测“金星凌日”时,如果将太阳看成质点,无法看到“金星凌日”现象,A错误;
B.“金星凌日”现象的成因是光的直线传播,当金星转到太阳与地球中间且三者在一条直线上时,金星挡住了沿直线传播的太阳光,人们看到太阳上的黑点实际上是金星,由此可知发生金星凌日现象时,金星位于地球和太阳之间,B错误;
C.根据开普勒第三定律
金星绕太阳的轨道半径小于地球绕太阳的轨道半径,所以金星绕太阳公转一周时间小于365天,C正确;
D.相同时间内,金星与太阳连线扫过的面积不等于地球与太阳连线扫过的面积,因为是不同的天体在围绕太阳运动,D错误。
故选C。
5.D
【解析】
A.公式式中,m、F、v、r都是可以直接测量的量,所以此式可以在实验室中进行验证,故A错误;
B.式中v、r、T都可以测量,因此用可以用实验验证,故B错误;
CD.开普勒第三定律公式是开普勒研究第谷的行星观测记录研究发现的,不能在实验室中验证,故C错误D正确。
故选D。
6.C
【解析】
由开普勒第二定律知,行星在A点速度最小,在B点速度最大,所以行星从A向B顺时针运动的过程中速度在增大,行星从B点顺时针运动到D点的时间小于从A点顺时针运动到C点的时间。
故选C。
7.B
【解析】
由公式
且依题意有
解得
故选B。
8.B
【解析】
地球绕太阳公转周期年,N年转N周,而该行星由于轨道半径大,周期也大,因而该行星N年应转周,故年
又因为行星和地球均绕太阳公转,由开普勒第三定律知
故选B。
9.C
【解析】
设地球绕太阳运动的周期为T,阋神星绕太阳运动的轨道半径为r,周期为T',由开普勒第三定律知
解得
ABD错误,C正确。
故选C。
10.B
【解析】
火星自转周期与地球接近,可知火星的同步卫星的周期为24h;根据开普勒第三定律
可得
故选B。
11.B
【解析】
由开普勒第三定律
同步卫星的周期为24小时,可知在中圆地球轨道上运行的卫星的周期小时≈13小时
故选B。
12.A
【解析】
因为行星在A点的速率大于在B点的速率,所以A点为近地点,太阳因该在F1点。
故选A。
13.D
【解析】
根据开普勒第三定律
则
两颗行星连续两次相距最近时
解得
故选D。
14.C
【解析】
在Ⅰ轨道上,r1=R+H=2R,在Ⅱ轨道上,半长轴为
根据开普勒第三定律知
解得
故选C。
15.D
【解析】
太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同,根据开普勒第三定律有
故ABC错误,D正确。
故选D。
16.A
【解析】
由题图可知,当行星处于最大视角处时,地球和行星的连线应与行星轨道相切。根据几何关系有
R行=R地sinθ
根据开普勒第三定律有
得年
故A正确,BCD错误。
故选A。
17.323km
【解析】
“神舟”五号飞船绕地球运动一周所用的时间为T1=h=1.5h
“静止”在赤道上空的卫星绕地球运动的周期为T2=24h,由开普勒第三定律=
解得r1=·r2
则“神舟”五号离地面的高度为h=r1-R地=·r2-R地
其中r2=5.67R地+R地=6.67R地
代入数据得h≈323km
18.(1)v1;(2)2062年
【解析】(1)由开普勒第二定律知v1>v2;
(2)由开普勒第三定律知
得
解得年
即下次飞近地球大约为(1986+76)年=2062年
19.1.28:1
【解析】
由开普勒第二定律知,卫星与地心的连线在相等时间内扫过的面积相等,故有
所以有运动速率之比
一、单选题
1.两颗人造卫星绕地球匀速圆周运动,周期之比是
,则轨道半径之比是( )
A.轨道半径之比是 B.轨道半径之比是
C.轨道半径之比是 D.轨道半径之比是
2.许多科学家在物理学的发展过程中做出了重要贡献,下列叙述错误的是( )
A.开普勒首先指出了行星绕太阳运动的轨道不是圆,而是椭圆
B.海王星是人们根据万有引力定律计算出其轨道后才发现的,被称为“笔尖下发现的行星”
C.开普勒总结出了行星运动的规律,并发现了万有引力定律
D.卡文迪什第一次在实验室里测出了万有引力常量G,被称为“第一个称出地球质量的人”
3.某行星绕太阳运动的椭圆轨道如图所示,和是椭圆轨道的两个焦点,行星在点的速率比在点的速率大,则太阳位于( )
A.位置 B.位置 C.位置 D.位置
4.在“金星凌日”的精彩天象中,观察到太阳表面上有颗小黑点缓慢走过,持续时间达六个半小时,那便是金星,如图所示。下面说法正确的是( )
A.观测“金星凌日”时可将太阳看成质点
B.地球在金星与太阳之间
C.金星绕太阳公转一周时间小于365天
D.相同时间内,金星与太阳连线扫过的面积等于地球与太阳连线扫过的面积
5.关于,,这三个等式的描述正确的是( )
A.不能在实验室验证
B.不能在实验室验证
C.可以在实验室验证
D.是开普勒用第谷观测数据计算推理得出的
6.如图所示是行星m绕太阳M运行情况的示意图,A点是远日点,B点是近日点,CD是椭圆轨道的短轴,下列说法中正确的是( )
A.行星运动到A点时速度最大
B.行星运动到C点或D点时速度最小
C.行星从C点顺时针运动到B点的过程中做加速运动
D.行星从B点顺时针运动到D点的时间与从A点顺时针运动到C点的时间相等
7.地球位于火星与太阳之间且三者在同一直线上时称为“火星冲日”。已知地球绕太阳做圆周运动的周期为T,火星绕太阳做圆周运动的轨道半径为地球绕太阳做圆周运动的轨道半径的n倍。则相邻两次“火星冲日”的时间差为( )
A. B. C. D.
8.某行星和地球绕太阳公转的轨道均可视为圆。每过N年,该行星会运行到日地连线的延长线上,如图所示该行星与地球的公转半径之比为( )
A. B. C. D.
9.阋神星是一个已知的第二大属于柯伊伯带及海王星外天体的矮行星,根据早期观测数据估算,阋神星比冥王星大,在公布其发现时曾被其发现者和等组织称为“第十大行星”。若将地球和阋神星绕太阳的运动看作匀速圆周运动,它们的运行轨道如图所示。已知阋神星绕太阳运行一周的时间约为557年,设地球绕太阳运行的轨道半径为R,则阋神星绕太阳运行的轨道半径约为( )
A. B. C. D.
10.2020年7月23日,我国首个火星探测器“天问一号”由长征五号运载火箭在海南文昌航天发射场成功发射。升空后,它将经历7个月左右的长途跋涉靠近火星,开展火星环绕、表面降落、巡视探测三大任务。假设环绕器绕火星运行的轨道半径约为火星同步卫星轨道半径的,火星自转周期与地球接近,那么环绕器绕火星一圈需要的时间最接近( )
A.1小时 B.3小时 C.6小时 D.12小时
11.中国北斗卫星导航系统已经组网完成,具备区域导航、定位和授时能力,定位精度为分米、厘米级别,测速精度为0.2米/秒,授时精度为10纳秒。北斗导航在轨工作的33颗卫星轨道半径有两种,一种是轨道半径为42000公里的同步地球轨道,另一种是轨道半径为28000公里的中圆地球轨道,则在中圆地球轨道上运行的卫星的周期约为( )
A.5小时 B.13小时 C.16小时 D.44小时
12.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点。已知行星在A点的速率大于在B点的速率,则太阳位于( )
A.F1点 B.F2点 C.O点 D.无法确定
13.如图所示,、两颗行星绕恒星做圆周运动,旋转方向相同,已知行星的轨道半径为行星的2倍,行星的周期为。不考虑、间的万有引力,则、两颗行星连续两次相距最近的时间间隔为( )
A. B. C. D.
14.若“嫦娥五号”卫星在距月球表面高度为H的环月轨道上做匀速圆周运动,其运行的周期为T;随后“嫦娥五号”在该轨道上某点采取措施,使卫星降至椭圆轨道Ⅱ上,如图所示,若近月点接近月球表面,而H等于月球半径,忽略月球自转及地球对卫星的影响,则“嫦娥五号”在轨道Ⅱ上的运行周期为( )
A. B. C. D.
15.太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同。下列能反映周期与轨道半径关系的图象中正确的是( )
A. B.
C. D.
16.如图所示,天文学家观测到某行星和地球在同一轨道平面内绕太阳做同向匀速圆周运动,且行星的轨道半径比地球的轨道半径小,地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角。当行星处于最大观察视角处时,是地球上的天文爱好者观察该行星的最佳时期,已知该行星的最大观察视角为θ,不计行星与地球之间的引力,则该行星环绕太阳运动的周期约为( )
A. 年 B.年 C.年 D.年
二、解答题
17.我国航天第一人杨利伟乘坐“神舟”五号载人飞船,在绕地球飞行了14圈、历时21小时后返回地面。已知地球半径R地=6.4×103km,“静止”在赤道上空的卫星的高度为5.67R地,则“神舟”五号离地多高?
18.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆。天文学家哈雷曾经在1662年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定时间就会再次出现。
(1)若这颗彗星在近日点的线速度为v1,在远日点的线速度为v2,则哪个线速度大?
(2)这颗彗星最近出现的时间是1986年,它下次飞近地球大约是哪一年?
19.1970年4月24日,我国发射了第一颗人造卫星,其近地点高度是km,远地点高度是km,设近地点处卫星的速率v1,远地点处卫星速率v2,则v1:v2为多少?(已知km)
参考答案
1.D
【解析】
根据开普勒第三定律
可得
所以
故选D。
2.C
【解析】
A.开普勒首先指出了行星绕太阳运动的轨道不是圆,而是椭圆,A正确;
B.海王星是人们根据万有引力定律计算出其轨道后才发现的,被称为“笔尖下发现的行星”,B正确。
C.万有引力定律是牛顿发现的,C错误;
D.卡文迪什第一次在实验室里测出了万有引力常量G,被称为“第一个称出地球质量的人”,D正确。
故错误的选C。
3.A
【解析】
根据开普勒第二定律,对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积,如果时间间隔相等,那么面积A=面积B,由此可知
所以A点为近日点,B点为远日点,则太阳是位于F2。
故选A。
4.C
【解析】
A.观测“金星凌日”时,如果将太阳看成质点,无法看到“金星凌日”现象,A错误;
B.“金星凌日”现象的成因是光的直线传播,当金星转到太阳与地球中间且三者在一条直线上时,金星挡住了沿直线传播的太阳光,人们看到太阳上的黑点实际上是金星,由此可知发生金星凌日现象时,金星位于地球和太阳之间,B错误;
C.根据开普勒第三定律
金星绕太阳的轨道半径小于地球绕太阳的轨道半径,所以金星绕太阳公转一周时间小于365天,C正确;
D.相同时间内,金星与太阳连线扫过的面积不等于地球与太阳连线扫过的面积,因为是不同的天体在围绕太阳运动,D错误。
故选C。
5.D
【解析】
A.公式式中,m、F、v、r都是可以直接测量的量,所以此式可以在实验室中进行验证,故A错误;
B.式中v、r、T都可以测量,因此用可以用实验验证,故B错误;
CD.开普勒第三定律公式是开普勒研究第谷的行星观测记录研究发现的,不能在实验室中验证,故C错误D正确。
故选D。
6.C
【解析】
由开普勒第二定律知,行星在A点速度最小,在B点速度最大,所以行星从A向B顺时针运动的过程中速度在增大,行星从B点顺时针运动到D点的时间小于从A点顺时针运动到C点的时间。
故选C。
7.B
【解析】
由公式
且依题意有
解得
故选B。
8.B
【解析】
地球绕太阳公转周期年,N年转N周,而该行星由于轨道半径大,周期也大,因而该行星N年应转周,故年
又因为行星和地球均绕太阳公转,由开普勒第三定律知
故选B。
9.C
【解析】
设地球绕太阳运动的周期为T,阋神星绕太阳运动的轨道半径为r,周期为T',由开普勒第三定律知
解得
ABD错误,C正确。
故选C。
10.B
【解析】
火星自转周期与地球接近,可知火星的同步卫星的周期为24h;根据开普勒第三定律
可得
故选B。
11.B
【解析】
由开普勒第三定律
同步卫星的周期为24小时,可知在中圆地球轨道上运行的卫星的周期小时≈13小时
故选B。
12.A
【解析】
因为行星在A点的速率大于在B点的速率,所以A点为近地点,太阳因该在F1点。
故选A。
13.D
【解析】
根据开普勒第三定律
则
两颗行星连续两次相距最近时
解得
故选D。
14.C
【解析】
在Ⅰ轨道上,r1=R+H=2R,在Ⅱ轨道上,半长轴为
根据开普勒第三定律知
解得
故选C。
15.D
【解析】
太阳系有八大行星,八大行星离地球的远近不同,绕太阳运转的周期也不相同,根据开普勒第三定律有
故ABC错误,D正确。
故选D。
16.A
【解析】
由题图可知,当行星处于最大视角处时,地球和行星的连线应与行星轨道相切。根据几何关系有
R行=R地sinθ
根据开普勒第三定律有
得年
故A正确,BCD错误。
故选A。
17.323km
【解析】
“神舟”五号飞船绕地球运动一周所用的时间为T1=h=1.5h
“静止”在赤道上空的卫星绕地球运动的周期为T2=24h,由开普勒第三定律=
解得r1=·r2
则“神舟”五号离地面的高度为h=r1-R地=·r2-R地
其中r2=5.67R地+R地=6.67R地
代入数据得h≈323km
18.(1)v1;(2)2062年
【解析】(1)由开普勒第二定律知v1>v2;
(2)由开普勒第三定律知
得
解得年
即下次飞近地球大约为(1986+76)年=2062年
19.1.28:1
【解析】
由开普勒第二定律知,卫星与地心的连线在相等时间内扫过的面积相等,故有
所以有运动速率之比
