1.4 实验:验证动量守恒定律同步练习 (word版含答案)
文档属性
| 名称 | 1.4 实验:验证动量守恒定律同步练习 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 209.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览




文档简介
实验:验证动量守恒定律练习
一、单选题(每道题只有一个正确答案)
在用气垫导轨“验证动量守恒定律”时,不需要测量的物理量是(????)
A. 滑块的质量 B. 挡光的时间 C. 挡光片的宽度 D. 光电门的高度
某中学实验小组的同学在“验证动量守恒定律”时,利用了如图所示的实验装置进行探究,下列说法正确的是(????)
A. 要求斜槽一定是光滑的且斜槽的末端必须水平
B. 入射球每次释放点的高度可以任意调节
C. 入射球和被碰球的直径必须相等
D. 入射球的质量必须与被碰球的质量相等
如图所示,用“碰撞实验器”可以验证动量守恒定律,即验证两个小球在水平轨道末端碰撞前后的动量守恒.入射小球质量为m1,被碰小球质量为m2,O点是小球抛出点在水平地面上的投影.实验时,先让入射小球多次从倾斜轨道上S位置静止释放,找到其平均落地点的位置,并记下此位置距O点的距离;然后把被碰小球静置于水平轨道末端,再将入射小球从倾斜轨道上S位置静止释放,与小球相撞,多次重复此过程,并分别找到它们平均落点的位置距O点的距离.则下列说法正确的是(??? )
A. 实验中要求两小球半径相等,且满足m1B. 实验中要求倾斜轨道必须光滑
C. 如果等式m1x3=m1x1+m2x2成立,可验证两小球碰撞过程动量守恒
D. 如果等式m1x22=m1x12+m2x32成立,可验证两小球发生的是弹性碰撞
A、B两小物块在一水平长直气垫导轨上相碰,用频闪照相机每隔t时间连续拍照四次,拍得如图所示的照片,已知四次拍照时两小物块均在图示坐标范围内,不计两小物块的大小及碰撞过程所用的时间,则由此照片可判断(????)
A. 第一次拍照时物块A在55cm处,并且mA:mB=1:3
B. 第一次拍照时物块A在10cm处,并且mA:mB=1:3
C. 第一次拍照时物块A在55cm处,并且mA:mB=1:5
D. 第一次拍照时物块A在10cm处,并且mA:mB=1:6
如图甲所示为“验证动量守恒定律”的实验装置示意图,已知a、b小球的质量分别为ma、mb。先单独将a球从斜槽上某点释放,小球a从轨道末端飞出后在水平地面上的平均落点为图甲中的P点;再将b球放于轨道末端,将a球从斜槽上相同的位置释放,多次实验,两球碰后在水平地面上的平均落点分别是图甲中M、N点。
本实验必须满足的条件是(????)
A. 斜槽轨道必须是光滑的
B. 入射小球a的质量必须等于被碰小球b的质量
C. 入射小球a每次都从斜槽上的同一位置无初速度释放
D. 要测量小球离开斜槽末端到水平面的飞行时间
在做“碰撞中的动量守恒”的实验中,入射球每次滚下都应从斜槽上的同一位置无初速释放,这是为了使(????)
A. 小球每次都能水平飞出槽口
B. 小球每次都以相同的速度飞出槽口
C. 小球在空中飞行的时间不变
D. 小球每次都能对心碰撞
用两小球a、b的碰撞验证动量守恒定律,实验装置如图,斜槽与水平槽圆滑连接。实验时先不放b球,使a球从斜槽上某一固定点M由静止滚下,落到位于水平地面的记录纸上留下痕迹;再把b球静置于水平槽前端边缘处,让a球仍从M处由静止滚下,a球和b球碰撞后分别落在记录纸上留下各自的痕迹,记录纸上的O点是重锤所指的位置。关于本实验下列说法不正确的是(????)
A. 两小球a、b的半径必须相同
B. 实验中需要用天平测出入射球a的质量m1和被碰球b的质量m2
C. 实验中需要测出斜槽轨道末端到水平地面的高度H
D. 实验中需要测出记录纸上O点到A、B、C各点的距离OA、OB、OC
在“探究碰撞中的不变量”实验中,设两球的质量分别为m1、m2,碰前的速度分别为v1,v2,碰后的速度分别为v1′,v2′,最终得到的结论是(????)
A. m1v1+m2v2=m1v1′+m2v2′ B. m1v12+m2v22=m1v1′2+m2v2′2
C. m1v1+m2v2=m1v1’+m2v2’ D. v1m1+v2m2=v1’m1+v2’m2
二、多选题(每道题有多个选项)
如图所示为“验证动量守恒定律”的实验装置,下列说法正确的是(????)
A. 悬挂两球的细绳长度要适当,且等长
B. 由静止释放小球以便较准确地计算小球碰前的速度
C. 两小球必须都是刚性球,且质量相同
D. 两小球碰后可以粘在一起共同运动
若用打点计时器做探究碰撞中的不变量实验时,下列哪些操作是正确的(????)
A. 相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了改变两车的质量
B. 相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了碰撞后粘在一起
C. 先接通打点计时器电源,再释放拖动纸带的小车
D. 先释放拖动纸带的小车,再接通打点计时器的电源
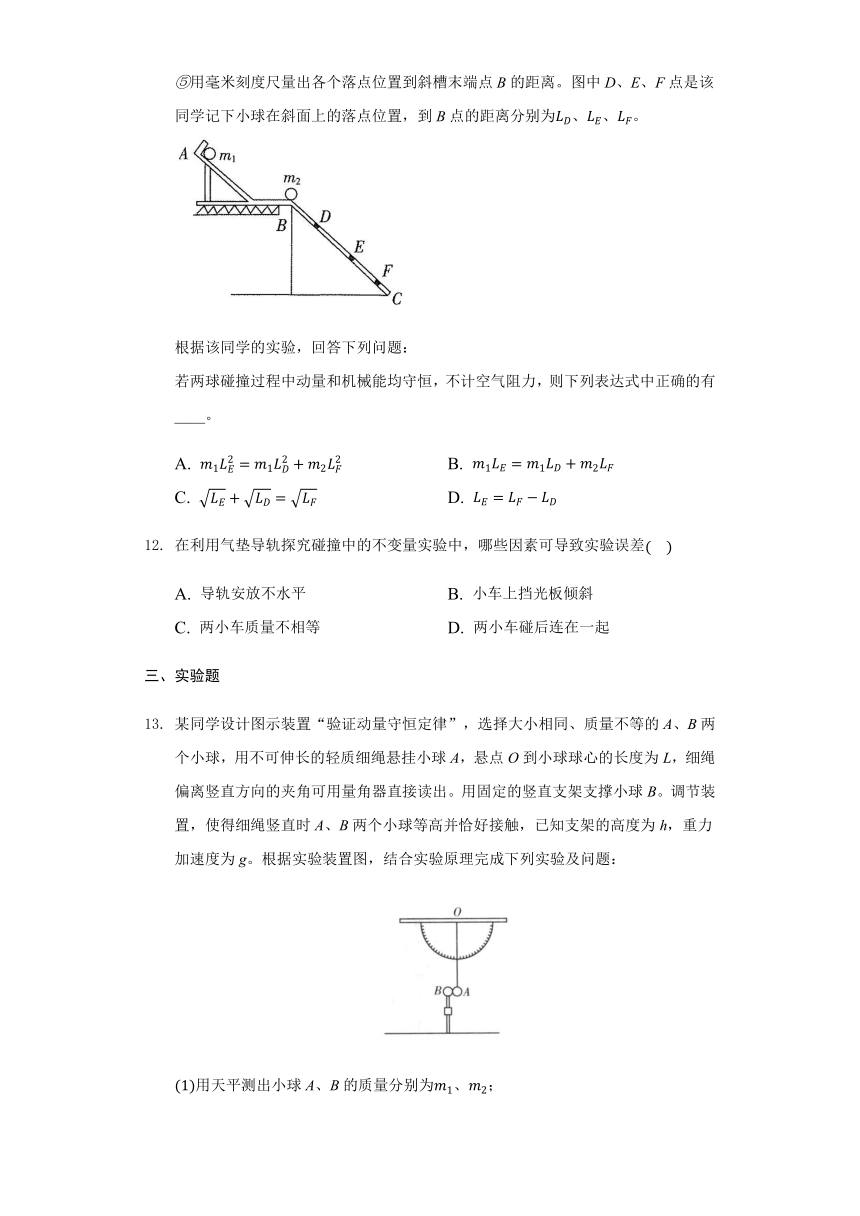
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量相差比较大的小球,按下述步骤做了实验:
①用天平测出两小球的质量分别为m1和m2,且m1>m2。
②按图示安装好实验器材,将斜槽AB固定在桌边,使槽的末端切线水平,将一斜面BC连接在斜槽末端。
③先不放小球m2,让小球m1从斜槽顶端A处由静止开始滚下,记下小球m1在斜面上的落点位置。
④将小球m2放在斜槽末端边缘处,让小球m1从斜槽顶端A处由静止开始滚下,使它们发生碰撞,分别记下小球m1和m2在斜面上的落点位置。
⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离。图中D、E、F点是该同学记下小球在斜面上的落点位置,到B点的距离分别为LD、LE、LF。
根据该同学的实验,回答下列问题:
若两球碰撞过程中动量和机械能均守恒,不计空气阻力,则下列表达式中正确的有____。
A. m1LE2=m1LD2+m2LF2 B. m1LE=m1LD+m2LF
C. LE+LD=LF D. LE=LF?LD
在利用气垫导轨探究碰撞中的不变量实验中,哪些因素可导致实验误差(????)
A. 导轨安放不水平 B. 小车上挡光板倾斜
C. 两小车质量不相等 D. 两小车碰后连在一起
三、实验题
某同学设计图示装置“验证动量守恒定律”,选择大小相同、质量不等的A、B两个小球,用不可伸长的轻质细绳悬挂小球A,悬点O到小球球心的长度为L,细绳偏离竖直方向的夹角可用量角器直接读出。用固定的竖直支架支撑小球B。调节装置,使得细绳竖直时A、B两个小球等高并恰好接触,已知支架的高度为h,重力加速度为g。根据实验装置图,结合实验原理完成下列实验及问题:
(1)用天平测出小球A、B的质量分别为m1、m2;
(2)将小球A拉至某一位置,读出细绳偏离竖直方向的夹角为θ1,由静止释放小球A;
(3)A与B发生碰撞后,A被反弹,细绳偏离竖直方向的最大夹角为θ2,小球B做平抛运动,在水平方向的位移为x;
(4)计算出碰撞前瞬间,A的速度大小为________,碰撞后瞬间B的速度大小为________;
(5)验证A、B碰撞前后动量守恒的表达式为________。
某同学用如图所示装置验证动量守恒定律。斜槽被竖直固定在水平桌面上,其末端Q伸出桌面外且切线水平;挡板b竖直固定,点O是Q点的水平投影点;小钢球1和玻璃球2的大小相等且均可视为质点;图中的P、M、N是小球与挡板的撞击点。请回答下列问题:
(1)第一次在不放玻璃球2时,将小钢球1从斜槽上E点静止释放,它撞击在挡板b上;第二次将玻璃球2放在斜槽末端Q处,小钢球仍从E点静止释放,它们均撞击在挡板b上。则第一次小钢球1撞击在挡板b上的________点(填“P”“M”或“N”)。
(2)要完成该实验,必须测量的物理量有________和________(填正确答案标号)。
A.小钢球1和玻璃球2的质量m1、m2? ? ? ? ? B.E、Q之间的竖直高度h
C.Q、O之间的水平距离x? ? ? ? ? ? ? ? ? ? ? ? ? ?D.OP、OM、ON的高度HP、HM、HN
(3)在误差允许范围内,关系式________成立,说明两球在碰撞过程中动量守恒。(用所测的物理量表示且为最简形式)
某同学在实验室使用半径相同的两个小球,按如图实验装置来验证动量守恒定律。他的主要实验操作如下:
①用天平测量a、b两球的质量m1和m2
②用游标卡尺测出两个小球的直径d???
③用刻度尺测出轨道末端距离地面的高度H
④用重锤线标出小球抛出点在水平地面上的白纸上的竖直投影点O
⑤在白纸上面放好复写纸,先不放b球,把a球从斜槽轨道上D点由静止释放,落到复写纸上,重复多次;再把b球放在斜槽轨道水平部分最右端,把a球仍从D点由静止释放,和b球相碰后,两球分别落在复写纸上的不同位置,重复多次
⑥用圆规在白纸上找到三个平均落点M、P和N,并用刻度尺测量出图中的OM、OP和ON的长度
(1)上述实验操作中不必要的步骤是_______________________
(2)如果满足关系式_____________________,则验证了系统碰撞过程中动量守恒。(用测量的物理量表示)
(3)实验测得:m1=30.0g,m2=10.0g,OM=16.10cm,OP=30.30cm,ON=40.60cm。则本实验的相对?误差是_______________? ?(保留一位有效数字,相对误差为|碰撞前后总动量之差碰前总动量|×100%?? )
为了验证“两小球碰撞过程中的动量守恒”,某同学用如图所示的装置进行了如下的操作:
①将斜槽轨道的末端调整水平,在一块平木板表面先后钉上白纸和复写纸,并将该木板竖直立于靠近槽口处,使小球a从斜槽轨道上某固定点处由静止释放,撞到木板并在白纸上留下痕迹O;
②将木板向右平移适当的距离固定,再使小球a从原固定点由静止释放,撞到木板并在白纸上留下痕迹P;
③把小球b静止放在斜槽轨道的水平段的最右端,让小球a仍从原固定点由静止释放,和小球b相碰后,两小球撞到木板并在白纸上留下痕迹M和N;
④用天平测出a、b两个小球的质量分别为ma和mb,用刻度尺测量白纸上O点到M、P、N三点的距离分别为yM、yP和yN。
根据上述实验,请回答下列问题:
(1)为了减小实验误差,选择入射球ma、被碰球mb时,应该使ma___mb。(填“大于”“等于”“小于”)
(2)小球a下滑过程中与斜槽轨道间存在摩擦力,这对实验结果___产生误差。(选填“会”或“不会”)
(3)小球a和b发生碰撞后,小球b在图中白纸上撞击痕迹应是___点。
(4)用本实验中所测得的物理量来验证两小球碰撞过程中动量守恒,其表达式为:_____________________。
验证动量守恒定律的实验装置如图所示。
(1)(多选)实验中必须满足的要求是______
A.斜槽轨道尽量光滑以减少误差;
B.斜槽轨道末端的切线必须水平;
C.入射球和被碰球的质量必须相等,且大小相同;
D.入射球每次必须从轨道的同一位置由静止释放。
(2)(多选)图中O点是小球抛出点在地面上的垂直投影。实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP,然后把被碰小球m2静置于水平轨道的末端,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并重复多次。
本实验还需要完成的必要步骤是_______(填选项前的符号)
A.用天平测量两个小球的质量m1、m2;
B.测量抛出点距地面的高度H;
C.分别找到m1、m2相碰后平均落地点的位置M、N;
D.测量平抛射程OM、ON。
(3)若两球发生弹性碰撞,则OM、ON、OP之间一定满足的关系是______(填选项前的符号)
A.OP+OM=ON;?????B.2OP=OM+ON;?????C.ON?OP=2OM。
答案和解析
1.【答案】D
2.【答案】C
3.【答案】D
4.【答案】B
【解析】解:由题意“四次拍照时两小物块均在图示坐标范围内”可以判断出,B物块在碰撞前处于静止状态,A在碰撞前沿x轴正方向运动,碰撞后A沿x轴负方向运动,B沿x轴正方向运动,由此得出碰撞发生在x=60cm的d点处(即B碰撞前所处的位置)。碰撞是在第三次拍照与第四次拍照之间发生,第四次拍照时A运动到x=55cm的e点处,B运动到x=65cm的f点处,从而可知第一次拍照时,A在x=10cm的a点处沿x轴正方向运动;第二、三次拍照时分别在x=30cm的b点处和x=50cm的c点处。
碰撞前,A的速度va=Labt,设碰撞后到第四次拍照的时间为t′,有t′=t?Lcdva=t2;
碰撞后,A、B的速度大小分别为:vA′=Ledt′,vb′=Ldft′,因Led=Ldf,所以va′和vb′的大小相等,都等于12va;
取向右为正方向,由动量守恒定律,有:mava=?mava′+mbvb′,以上各式联立,解得:mA:mB=1:3,故ACD错误,B正确。
5.【答案】C
【解答】
A.“验证动量守恒定律”的实验中,是通过平抛运动的基本规律求解碰撞前后的速度的,只要离开轨道后做平抛运动,对斜槽是否光滑没有要求,故A错误;
B.为了保证小球碰撞为对心正碰,且碰后不反弹,要求ma>mb,ra=rb,故B错误;
C.要保证碰撞前的速度相同,所以入射球每次都要从同一高度由静止滚下,故C正确;
D.小球从同一高度做平抛运动,飞行的时间t相同,而水平方向的运动为匀速直线运动,故水平位移x=vt,而小球每次做平抛运动的时间均相同,所以只要测出小球飞行的水平位移,就可以用水平位移的测量值代替平抛初速度,故D错误。
6.【答案】B
【解析】解:入射小球每次滚下都应从斜槽上的同一位置无初速的释放,是为了使小球每次都以相同的速度飞出槽口;故B正确;
而只要末端水平,小球即可以做平抛运动,与起点无关,同时时间由高度决定,而要使小球做对心碰撞,应该使两小球的半径相同,故ACD错误;
7.【答案】C
【解析】解:A、要保证碰撞后都做平抛运动,两球要发生正碰,碰撞的瞬间,入射球与被碰球的球心应在同一水平高度,两球心的连线应与轨道末端的切线平行,因此两球半径必须相同,故A正确;
B、根据实验原理可知,实验中需要用天平测出入射球a的质量m1和被碰球b的质量m2,故B正确;
CD、为了验证动量守恒可知,本实验中需要测量A球和B球的质量和两球的水平射程OA、OB、OC;不需要测量斜槽轨道末端到水平地面的高度,故C不正确;D正确。
本题选不正确的,
8.【答案】A
【解答】
ACD、在碰撞中忽回复外力可以认为总动量守恒,则可知m1v1+m2v2=m1v1′+m2v2′;故 A正确,CD错误;
B、由于碰撞并不一定是完全弹性碰撞,故不能证机械能守恒,故B不一定成立;故 B错误;
9.【答案】ABD
10.【答案】BC
【解答】
AB、相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了碰撞后粘在一起,不是为了改变车的质量,故A错误,B正确;
CD、为了能测出小车从初速度为零开始的运动,应先接通电源再释放纸带;故C正确,D错误;
11.【答案】BC
【解答】
设斜面倾角为θ,小球落点到B点的距离为L,小球从B点抛出时速度为v,则竖直方向有Lsin?θ=12gt2,水平方向有Lcos?θ=vt;
解得v=Lcos?θt=Lgcos2θ2sin?θ,所以v∝L。
由题意分析得,只要满足m1v1=m2v2+m1v1′就可验证动量守恒定律,即如果满足m1LE=m1LD+m2LF,就可说明两球碰撞过程中动量守恒;
若两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失,则要满足关系式,整理得m1LE=m1LD+m2LF,故B项正确;
由m1LE=m1LD+m2LF和m1LE=m1LD+m2LF两式联立可得LE+LD=LF,C项正确。
12.【答案】AB
【解析】解:A、导轨不水平,小车速度将受重力的影响,从而导致实验误差,故A正确;
B、挡光板倾斜会导致挡光板宽度不等于挡光阶段小车通过的位移,使计算速度出现误差;故B正确;
C、两小车质量不相等,系统碰撞前后动量仍然守恒,故不会导致实验误差,故C错误;
D、两小车碰后连在一起是完全非弹性碰撞,系统碰撞前后动量仍然守恒,故不会导致实验误差,故D错误;
13.【答案】(4)2gL1?cosθ1?;?xg2?;
(5)m12gL1?cosθ1=?m12gL1?cosθ2+m2xg2?。
【解答】
(4)对A球由动能定理可知:m1gL1?cosθ1=12m1vA2,解得vA=2gL1?cosθ1;由平抛运动规律可知,水平方向有x=v′Bt,竖直方向有?=12gt2,联立解得的v′B=xg2?。
(5)碰撞后细绳偏离竖直方向的最大夹角为θ2,由动能定理得?m1gL1?cosθ2=0?12m1v′A2,解得v′A=2gL1?cosθ2,由动量守恒定律可知,m1vA=?m1v′A+m2v′B,联立以上各式可得m12gL1?cosθ1=?m12gL1?cosθ2+m2xg2?。
14.【答案】(1)M;
(2)A(或D);D(或A);
(3)m1HM=m1HN+m2HP(若填成m1?HMHM=m1?HNHN+m2?HPHP给2分)。
【解答】
(1)第一次在不放玻璃球2时,小钢球1撞击在挡板b上的M点;
(2)小球平抛的速度v=xt,每次实验两小球撞击挡板时的水平距离x都相等,而时间由小球下落高度决定,因此只要测量小钢球1和玻璃球2的质量m1、m2,以及OP、OM、ON的高度HP、HM、HN,即可验证动量守恒,故AD正确,BC错误;
(3)根据动量守恒定律有:m1v1=m1v1′+m2v2′
小钢球1碰撞前的速度:v1=xt1
小钢球1碰撞后的速度:v1′=xt1′
玻璃球2碰撞后的速度:v2′=xt2′
根据竖直方向为自由落体运动,可得:t1=2HMg,t1′=2HNg,t2′=2HPg
代入动量守恒表达式,化简得:m1HM=m1HN+m2HP
故答案为:(1)M;(2)A(或D);D(或A);(3)m1HM=m1HN+m2HP。
15.【答案】(1)②③;(2)m1OP=m1OM+m2ON? ;(3)2%。
【解答】
(1)
根据实验原理可知,在该实验中,小球做平抛运动,H相等,时间t就相等,水平位移x=vt,与v成正比,因此可以用位移x来代替速度v,需要知道两小球的质量和水平位移,实验中只需保证两球直径相同即可,不需要测出求得直径,故不必要的步骤是②③;
(2)
由平抛运动规律知,小球在空中运动时间相同,设为t,由动量守恒定律知:
m1v0=m1v1+m2v2,
两边同时乘以时间t得:
m1v0t=m1v1t+m2v2t,
即:m1OP=m1OM+m2ON,
(3)根据公式本实验的相对误差为;
故答案为:(1)②③;(2)m1OP=m1OM+m2ON? ;(3)2%。
16.【答案】(1)大于;(2)不会;(3)M;? (4)mayp=mayN+mbyM?。
【解答】
(1)为防止碰撞后入射球反弹,入射球的质量应大于被碰球的质量,即:应该使ma大于mb。
(2)只要由静止从同一位置释放小球,小球到达轨道底端时速度相等,小球a下滑过程中与斜槽轨道间存在摩擦力,这对实验结果不会产生误差。
(3)小球a和b发生碰撞后,小球b的速度大于a的速度,大于a碰撞前的速度,由于小球做平抛运动的水平位移相等,
小球的初速度越大,小球运动时间越短,小球下落高度越小,由此可知,碰撞后小球b下落时间最大,下落高度最小,小球b在图中白纸上撞击痕迹应是M点。
(4)小球离开轨道后做平抛运动,设木板与抛出点之间的距离为x,由平抛运动规律得:
水平方向:x=vt,竖直方向:?=12gt2
解得:v=xg2??。
碰撞前,小球a落在图中的P点,设其水平初速度为v0.小球a和b发生碰撞后,a的落点在图中的N点,
设其水平初速度为v1,m2的落点是图中的M点,设其水平初速度为v2.小球碰撞的过程中若动量守恒,
则有:mav0=mav1+mbv2
即为:ma·xg2yP??=ma·xg2yN?+mb·xg2yM
则验证两球碰撞过程中动量守恒的表达式为:mayp=mayN+mbyM
故答案为:(1)大于;(2)不会;(3)M;? (4)mayp=mayN+mbyM?。
17.【答案】(1)BD;? ? (2)ACD;? ?(3)? A。
【解答】
(1)A.斜槽轨道不需要光滑,只需要保证每次平抛的初速度相同,即可,故A错误;
B.小球离开轨道后做平抛运动,故斜槽轨道末端的切线必须水平,故B正确;
C.为了保证碰撞后不反弹,入射球的质量应大于被碰球的质量,且大小相同,故C错误;
D.为保证每次平抛的初速度相同,入射球每次必须从轨道的同一位置由静止释放,故D正确。
(2)如果碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:m1v0=m1v1+m2v2,
小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间t相等,
上式两边同时乘以t得:m1v0t=m1v1t+m2v2t,得:m1OP=m1OM+m2ON,
因此实验需要过程为:测量两球的质量、确定落点从而确定小球的水平位移;
故选ACD。
(3)如果碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:m1v1=m1v2+m2v3,
如果碰撞为弹性碰撞,碰撞过程机械能守恒,由机械能守恒定律得:12m1v12=12m1v22+12m2v32
解得:v1=?m1?m2?m1+m2?v0,v2=?2m1m1+m2?v0,显然:v2?v1=v0,因平抛运动中的时间相等,所以有:OP=ON?OM,故A正确,BC错误;
一、单选题(每道题只有一个正确答案)
在用气垫导轨“验证动量守恒定律”时,不需要测量的物理量是(????)
A. 滑块的质量 B. 挡光的时间 C. 挡光片的宽度 D. 光电门的高度
某中学实验小组的同学在“验证动量守恒定律”时,利用了如图所示的实验装置进行探究,下列说法正确的是(????)
A. 要求斜槽一定是光滑的且斜槽的末端必须水平
B. 入射球每次释放点的高度可以任意调节
C. 入射球和被碰球的直径必须相等
D. 入射球的质量必须与被碰球的质量相等
如图所示,用“碰撞实验器”可以验证动量守恒定律,即验证两个小球在水平轨道末端碰撞前后的动量守恒.入射小球质量为m1,被碰小球质量为m2,O点是小球抛出点在水平地面上的投影.实验时,先让入射小球多次从倾斜轨道上S位置静止释放,找到其平均落地点的位置,并记下此位置距O点的距离;然后把被碰小球静置于水平轨道末端,再将入射小球从倾斜轨道上S位置静止释放,与小球相撞,多次重复此过程,并分别找到它们平均落点的位置距O点的距离.则下列说法正确的是(??? )
A. 实验中要求两小球半径相等,且满足m1
C. 如果等式m1x3=m1x1+m2x2成立,可验证两小球碰撞过程动量守恒
D. 如果等式m1x22=m1x12+m2x32成立,可验证两小球发生的是弹性碰撞
A、B两小物块在一水平长直气垫导轨上相碰,用频闪照相机每隔t时间连续拍照四次,拍得如图所示的照片,已知四次拍照时两小物块均在图示坐标范围内,不计两小物块的大小及碰撞过程所用的时间,则由此照片可判断(????)
A. 第一次拍照时物块A在55cm处,并且mA:mB=1:3
B. 第一次拍照时物块A在10cm处,并且mA:mB=1:3
C. 第一次拍照时物块A在55cm处,并且mA:mB=1:5
D. 第一次拍照时物块A在10cm处,并且mA:mB=1:6
如图甲所示为“验证动量守恒定律”的实验装置示意图,已知a、b小球的质量分别为ma、mb。先单独将a球从斜槽上某点释放,小球a从轨道末端飞出后在水平地面上的平均落点为图甲中的P点;再将b球放于轨道末端,将a球从斜槽上相同的位置释放,多次实验,两球碰后在水平地面上的平均落点分别是图甲中M、N点。
本实验必须满足的条件是(????)
A. 斜槽轨道必须是光滑的
B. 入射小球a的质量必须等于被碰小球b的质量
C. 入射小球a每次都从斜槽上的同一位置无初速度释放
D. 要测量小球离开斜槽末端到水平面的飞行时间
在做“碰撞中的动量守恒”的实验中,入射球每次滚下都应从斜槽上的同一位置无初速释放,这是为了使(????)
A. 小球每次都能水平飞出槽口
B. 小球每次都以相同的速度飞出槽口
C. 小球在空中飞行的时间不变
D. 小球每次都能对心碰撞
用两小球a、b的碰撞验证动量守恒定律,实验装置如图,斜槽与水平槽圆滑连接。实验时先不放b球,使a球从斜槽上某一固定点M由静止滚下,落到位于水平地面的记录纸上留下痕迹;再把b球静置于水平槽前端边缘处,让a球仍从M处由静止滚下,a球和b球碰撞后分别落在记录纸上留下各自的痕迹,记录纸上的O点是重锤所指的位置。关于本实验下列说法不正确的是(????)
A. 两小球a、b的半径必须相同
B. 实验中需要用天平测出入射球a的质量m1和被碰球b的质量m2
C. 实验中需要测出斜槽轨道末端到水平地面的高度H
D. 实验中需要测出记录纸上O点到A、B、C各点的距离OA、OB、OC
在“探究碰撞中的不变量”实验中,设两球的质量分别为m1、m2,碰前的速度分别为v1,v2,碰后的速度分别为v1′,v2′,最终得到的结论是(????)
A. m1v1+m2v2=m1v1′+m2v2′ B. m1v12+m2v22=m1v1′2+m2v2′2
C. m1v1+m2v2=m1v1’+m2v2’ D. v1m1+v2m2=v1’m1+v2’m2
二、多选题(每道题有多个选项)
如图所示为“验证动量守恒定律”的实验装置,下列说法正确的是(????)
A. 悬挂两球的细绳长度要适当,且等长
B. 由静止释放小球以便较准确地计算小球碰前的速度
C. 两小球必须都是刚性球,且质量相同
D. 两小球碰后可以粘在一起共同运动
若用打点计时器做探究碰撞中的不变量实验时,下列哪些操作是正确的(????)
A. 相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了改变两车的质量
B. 相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了碰撞后粘在一起
C. 先接通打点计时器电源,再释放拖动纸带的小车
D. 先释放拖动纸带的小车,再接通打点计时器的电源
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量相差比较大的小球,按下述步骤做了实验:
①用天平测出两小球的质量分别为m1和m2,且m1>m2。
②按图示安装好实验器材,将斜槽AB固定在桌边,使槽的末端切线水平,将一斜面BC连接在斜槽末端。
③先不放小球m2,让小球m1从斜槽顶端A处由静止开始滚下,记下小球m1在斜面上的落点位置。
④将小球m2放在斜槽末端边缘处,让小球m1从斜槽顶端A处由静止开始滚下,使它们发生碰撞,分别记下小球m1和m2在斜面上的落点位置。
⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离。图中D、E、F点是该同学记下小球在斜面上的落点位置,到B点的距离分别为LD、LE、LF。
根据该同学的实验,回答下列问题:
若两球碰撞过程中动量和机械能均守恒,不计空气阻力,则下列表达式中正确的有____。
A. m1LE2=m1LD2+m2LF2 B. m1LE=m1LD+m2LF
C. LE+LD=LF D. LE=LF?LD
在利用气垫导轨探究碰撞中的不变量实验中,哪些因素可导致实验误差(????)
A. 导轨安放不水平 B. 小车上挡光板倾斜
C. 两小车质量不相等 D. 两小车碰后连在一起
三、实验题
某同学设计图示装置“验证动量守恒定律”,选择大小相同、质量不等的A、B两个小球,用不可伸长的轻质细绳悬挂小球A,悬点O到小球球心的长度为L,细绳偏离竖直方向的夹角可用量角器直接读出。用固定的竖直支架支撑小球B。调节装置,使得细绳竖直时A、B两个小球等高并恰好接触,已知支架的高度为h,重力加速度为g。根据实验装置图,结合实验原理完成下列实验及问题:
(1)用天平测出小球A、B的质量分别为m1、m2;
(2)将小球A拉至某一位置,读出细绳偏离竖直方向的夹角为θ1,由静止释放小球A;
(3)A与B发生碰撞后,A被反弹,细绳偏离竖直方向的最大夹角为θ2,小球B做平抛运动,在水平方向的位移为x;
(4)计算出碰撞前瞬间,A的速度大小为________,碰撞后瞬间B的速度大小为________;
(5)验证A、B碰撞前后动量守恒的表达式为________。
某同学用如图所示装置验证动量守恒定律。斜槽被竖直固定在水平桌面上,其末端Q伸出桌面外且切线水平;挡板b竖直固定,点O是Q点的水平投影点;小钢球1和玻璃球2的大小相等且均可视为质点;图中的P、M、N是小球与挡板的撞击点。请回答下列问题:
(1)第一次在不放玻璃球2时,将小钢球1从斜槽上E点静止释放,它撞击在挡板b上;第二次将玻璃球2放在斜槽末端Q处,小钢球仍从E点静止释放,它们均撞击在挡板b上。则第一次小钢球1撞击在挡板b上的________点(填“P”“M”或“N”)。
(2)要完成该实验,必须测量的物理量有________和________(填正确答案标号)。
A.小钢球1和玻璃球2的质量m1、m2? ? ? ? ? B.E、Q之间的竖直高度h
C.Q、O之间的水平距离x? ? ? ? ? ? ? ? ? ? ? ? ? ?D.OP、OM、ON的高度HP、HM、HN
(3)在误差允许范围内,关系式________成立,说明两球在碰撞过程中动量守恒。(用所测的物理量表示且为最简形式)
某同学在实验室使用半径相同的两个小球,按如图实验装置来验证动量守恒定律。他的主要实验操作如下:
①用天平测量a、b两球的质量m1和m2
②用游标卡尺测出两个小球的直径d???
③用刻度尺测出轨道末端距离地面的高度H
④用重锤线标出小球抛出点在水平地面上的白纸上的竖直投影点O
⑤在白纸上面放好复写纸,先不放b球,把a球从斜槽轨道上D点由静止释放,落到复写纸上,重复多次;再把b球放在斜槽轨道水平部分最右端,把a球仍从D点由静止释放,和b球相碰后,两球分别落在复写纸上的不同位置,重复多次
⑥用圆规在白纸上找到三个平均落点M、P和N,并用刻度尺测量出图中的OM、OP和ON的长度
(1)上述实验操作中不必要的步骤是_______________________
(2)如果满足关系式_____________________,则验证了系统碰撞过程中动量守恒。(用测量的物理量表示)
(3)实验测得:m1=30.0g,m2=10.0g,OM=16.10cm,OP=30.30cm,ON=40.60cm。则本实验的相对?误差是_______________? ?(保留一位有效数字,相对误差为|碰撞前后总动量之差碰前总动量|×100%?? )
为了验证“两小球碰撞过程中的动量守恒”,某同学用如图所示的装置进行了如下的操作:
①将斜槽轨道的末端调整水平,在一块平木板表面先后钉上白纸和复写纸,并将该木板竖直立于靠近槽口处,使小球a从斜槽轨道上某固定点处由静止释放,撞到木板并在白纸上留下痕迹O;
②将木板向右平移适当的距离固定,再使小球a从原固定点由静止释放,撞到木板并在白纸上留下痕迹P;
③把小球b静止放在斜槽轨道的水平段的最右端,让小球a仍从原固定点由静止释放,和小球b相碰后,两小球撞到木板并在白纸上留下痕迹M和N;
④用天平测出a、b两个小球的质量分别为ma和mb,用刻度尺测量白纸上O点到M、P、N三点的距离分别为yM、yP和yN。
根据上述实验,请回答下列问题:
(1)为了减小实验误差,选择入射球ma、被碰球mb时,应该使ma___mb。(填“大于”“等于”“小于”)
(2)小球a下滑过程中与斜槽轨道间存在摩擦力,这对实验结果___产生误差。(选填“会”或“不会”)
(3)小球a和b发生碰撞后,小球b在图中白纸上撞击痕迹应是___点。
(4)用本实验中所测得的物理量来验证两小球碰撞过程中动量守恒,其表达式为:_____________________。
验证动量守恒定律的实验装置如图所示。
(1)(多选)实验中必须满足的要求是______
A.斜槽轨道尽量光滑以减少误差;
B.斜槽轨道末端的切线必须水平;
C.入射球和被碰球的质量必须相等,且大小相同;
D.入射球每次必须从轨道的同一位置由静止释放。
(2)(多选)图中O点是小球抛出点在地面上的垂直投影。实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP,然后把被碰小球m2静置于水平轨道的末端,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并重复多次。
本实验还需要完成的必要步骤是_______(填选项前的符号)
A.用天平测量两个小球的质量m1、m2;
B.测量抛出点距地面的高度H;
C.分别找到m1、m2相碰后平均落地点的位置M、N;
D.测量平抛射程OM、ON。
(3)若两球发生弹性碰撞,则OM、ON、OP之间一定满足的关系是______(填选项前的符号)
A.OP+OM=ON;?????B.2OP=OM+ON;?????C.ON?OP=2OM。
答案和解析
1.【答案】D
2.【答案】C
3.【答案】D
4.【答案】B
【解析】解:由题意“四次拍照时两小物块均在图示坐标范围内”可以判断出,B物块在碰撞前处于静止状态,A在碰撞前沿x轴正方向运动,碰撞后A沿x轴负方向运动,B沿x轴正方向运动,由此得出碰撞发生在x=60cm的d点处(即B碰撞前所处的位置)。碰撞是在第三次拍照与第四次拍照之间发生,第四次拍照时A运动到x=55cm的e点处,B运动到x=65cm的f点处,从而可知第一次拍照时,A在x=10cm的a点处沿x轴正方向运动;第二、三次拍照时分别在x=30cm的b点处和x=50cm的c点处。
碰撞前,A的速度va=Labt,设碰撞后到第四次拍照的时间为t′,有t′=t?Lcdva=t2;
碰撞后,A、B的速度大小分别为:vA′=Ledt′,vb′=Ldft′,因Led=Ldf,所以va′和vb′的大小相等,都等于12va;
取向右为正方向,由动量守恒定律,有:mava=?mava′+mbvb′,以上各式联立,解得:mA:mB=1:3,故ACD错误,B正确。
5.【答案】C
【解答】
A.“验证动量守恒定律”的实验中,是通过平抛运动的基本规律求解碰撞前后的速度的,只要离开轨道后做平抛运动,对斜槽是否光滑没有要求,故A错误;
B.为了保证小球碰撞为对心正碰,且碰后不反弹,要求ma>mb,ra=rb,故B错误;
C.要保证碰撞前的速度相同,所以入射球每次都要从同一高度由静止滚下,故C正确;
D.小球从同一高度做平抛运动,飞行的时间t相同,而水平方向的运动为匀速直线运动,故水平位移x=vt,而小球每次做平抛运动的时间均相同,所以只要测出小球飞行的水平位移,就可以用水平位移的测量值代替平抛初速度,故D错误。
6.【答案】B
【解析】解:入射小球每次滚下都应从斜槽上的同一位置无初速的释放,是为了使小球每次都以相同的速度飞出槽口;故B正确;
而只要末端水平,小球即可以做平抛运动,与起点无关,同时时间由高度决定,而要使小球做对心碰撞,应该使两小球的半径相同,故ACD错误;
7.【答案】C
【解析】解:A、要保证碰撞后都做平抛运动,两球要发生正碰,碰撞的瞬间,入射球与被碰球的球心应在同一水平高度,两球心的连线应与轨道末端的切线平行,因此两球半径必须相同,故A正确;
B、根据实验原理可知,实验中需要用天平测出入射球a的质量m1和被碰球b的质量m2,故B正确;
CD、为了验证动量守恒可知,本实验中需要测量A球和B球的质量和两球的水平射程OA、OB、OC;不需要测量斜槽轨道末端到水平地面的高度,故C不正确;D正确。
本题选不正确的,
8.【答案】A
【解答】
ACD、在碰撞中忽回复外力可以认为总动量守恒,则可知m1v1+m2v2=m1v1′+m2v2′;故 A正确,CD错误;
B、由于碰撞并不一定是完全弹性碰撞,故不能证机械能守恒,故B不一定成立;故 B错误;
9.【答案】ABD
10.【答案】BC
【解答】
AB、相互作用的两车上,一个装上撞针,一个装上橡皮泥,是为了碰撞后粘在一起,不是为了改变车的质量,故A错误,B正确;
CD、为了能测出小车从初速度为零开始的运动,应先接通电源再释放纸带;故C正确,D错误;
11.【答案】BC
【解答】
设斜面倾角为θ,小球落点到B点的距离为L,小球从B点抛出时速度为v,则竖直方向有Lsin?θ=12gt2,水平方向有Lcos?θ=vt;
解得v=Lcos?θt=Lgcos2θ2sin?θ,所以v∝L。
由题意分析得,只要满足m1v1=m2v2+m1v1′就可验证动量守恒定律,即如果满足m1LE=m1LD+m2LF,就可说明两球碰撞过程中动量守恒;
若两小球的碰撞是弹性碰撞,则碰撞前后机械能没有损失,则要满足关系式,整理得m1LE=m1LD+m2LF,故B项正确;
由m1LE=m1LD+m2LF和m1LE=m1LD+m2LF两式联立可得LE+LD=LF,C项正确。
12.【答案】AB
【解析】解:A、导轨不水平,小车速度将受重力的影响,从而导致实验误差,故A正确;
B、挡光板倾斜会导致挡光板宽度不等于挡光阶段小车通过的位移,使计算速度出现误差;故B正确;
C、两小车质量不相等,系统碰撞前后动量仍然守恒,故不会导致实验误差,故C错误;
D、两小车碰后连在一起是完全非弹性碰撞,系统碰撞前后动量仍然守恒,故不会导致实验误差,故D错误;
13.【答案】(4)2gL1?cosθ1?;?xg2?;
(5)m12gL1?cosθ1=?m12gL1?cosθ2+m2xg2?。
【解答】
(4)对A球由动能定理可知:m1gL1?cosθ1=12m1vA2,解得vA=2gL1?cosθ1;由平抛运动规律可知,水平方向有x=v′Bt,竖直方向有?=12gt2,联立解得的v′B=xg2?。
(5)碰撞后细绳偏离竖直方向的最大夹角为θ2,由动能定理得?m1gL1?cosθ2=0?12m1v′A2,解得v′A=2gL1?cosθ2,由动量守恒定律可知,m1vA=?m1v′A+m2v′B,联立以上各式可得m12gL1?cosθ1=?m12gL1?cosθ2+m2xg2?。
14.【答案】(1)M;
(2)A(或D);D(或A);
(3)m1HM=m1HN+m2HP(若填成m1?HMHM=m1?HNHN+m2?HPHP给2分)。
【解答】
(1)第一次在不放玻璃球2时,小钢球1撞击在挡板b上的M点;
(2)小球平抛的速度v=xt,每次实验两小球撞击挡板时的水平距离x都相等,而时间由小球下落高度决定,因此只要测量小钢球1和玻璃球2的质量m1、m2,以及OP、OM、ON的高度HP、HM、HN,即可验证动量守恒,故AD正确,BC错误;
(3)根据动量守恒定律有:m1v1=m1v1′+m2v2′
小钢球1碰撞前的速度:v1=xt1
小钢球1碰撞后的速度:v1′=xt1′
玻璃球2碰撞后的速度:v2′=xt2′
根据竖直方向为自由落体运动,可得:t1=2HMg,t1′=2HNg,t2′=2HPg
代入动量守恒表达式,化简得:m1HM=m1HN+m2HP
故答案为:(1)M;(2)A(或D);D(或A);(3)m1HM=m1HN+m2HP。
15.【答案】(1)②③;(2)m1OP=m1OM+m2ON? ;(3)2%。
【解答】
(1)
根据实验原理可知,在该实验中,小球做平抛运动,H相等,时间t就相等,水平位移x=vt,与v成正比,因此可以用位移x来代替速度v,需要知道两小球的质量和水平位移,实验中只需保证两球直径相同即可,不需要测出求得直径,故不必要的步骤是②③;
(2)
由平抛运动规律知,小球在空中运动时间相同,设为t,由动量守恒定律知:
m1v0=m1v1+m2v2,
两边同时乘以时间t得:
m1v0t=m1v1t+m2v2t,
即:m1OP=m1OM+m2ON,
(3)根据公式本实验的相对误差为;
故答案为:(1)②③;(2)m1OP=m1OM+m2ON? ;(3)2%。
16.【答案】(1)大于;(2)不会;(3)M;? (4)mayp=mayN+mbyM?。
【解答】
(1)为防止碰撞后入射球反弹,入射球的质量应大于被碰球的质量,即:应该使ma大于mb。
(2)只要由静止从同一位置释放小球,小球到达轨道底端时速度相等,小球a下滑过程中与斜槽轨道间存在摩擦力,这对实验结果不会产生误差。
(3)小球a和b发生碰撞后,小球b的速度大于a的速度,大于a碰撞前的速度,由于小球做平抛运动的水平位移相等,
小球的初速度越大,小球运动时间越短,小球下落高度越小,由此可知,碰撞后小球b下落时间最大,下落高度最小,小球b在图中白纸上撞击痕迹应是M点。
(4)小球离开轨道后做平抛运动,设木板与抛出点之间的距离为x,由平抛运动规律得:
水平方向:x=vt,竖直方向:?=12gt2
解得:v=xg2??。
碰撞前,小球a落在图中的P点,设其水平初速度为v0.小球a和b发生碰撞后,a的落点在图中的N点,
设其水平初速度为v1,m2的落点是图中的M点,设其水平初速度为v2.小球碰撞的过程中若动量守恒,
则有:mav0=mav1+mbv2
即为:ma·xg2yP??=ma·xg2yN?+mb·xg2yM
则验证两球碰撞过程中动量守恒的表达式为:mayp=mayN+mbyM
故答案为:(1)大于;(2)不会;(3)M;? (4)mayp=mayN+mbyM?。
17.【答案】(1)BD;? ? (2)ACD;? ?(3)? A。
【解答】
(1)A.斜槽轨道不需要光滑,只需要保证每次平抛的初速度相同,即可,故A错误;
B.小球离开轨道后做平抛运动,故斜槽轨道末端的切线必须水平,故B正确;
C.为了保证碰撞后不反弹,入射球的质量应大于被碰球的质量,且大小相同,故C错误;
D.为保证每次平抛的初速度相同,入射球每次必须从轨道的同一位置由静止释放,故D正确。
(2)如果碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:m1v0=m1v1+m2v2,
小球离开轨道后做平抛运动,它们抛出点的高度相等,在空中的运动时间t相等,
上式两边同时乘以t得:m1v0t=m1v1t+m2v2t,得:m1OP=m1OM+m2ON,
因此实验需要过程为:测量两球的质量、确定落点从而确定小球的水平位移;
故选ACD。
(3)如果碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:m1v1=m1v2+m2v3,
如果碰撞为弹性碰撞,碰撞过程机械能守恒,由机械能守恒定律得:12m1v12=12m1v22+12m2v32
解得:v1=?m1?m2?m1+m2?v0,v2=?2m1m1+m2?v0,显然:v2?v1=v0,因平抛运动中的时间相等,所以有:OP=ON?OM,故A正确,BC错误;
