2.3 简谐运动的回复力和能量同步练习 (word版含答案)
文档属性
| 名称 | 2.3 简谐运动的回复力和能量同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 215.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-25 16:36:59 | ||
图片预览



文档简介
简谐运动的回复力和能量练习
一、单选题(每道题只有一个正确答案)
某质点做简谐运动,其位移随时间变化的关系式为x=5sinπ4tcm,则下列关于质点运动的说法中正确的是(????)
A. 质点做简谐运动的振幅为10cm B. 质点做简谐运动的周期为4s
C. 在t=4s时质点的速度最大 D. 在t=4s时质点的加速度最大
把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置O在A、B间振动,如图所示,下列结论正确的是(????)
A. 小球在O位置时,动能最大,加速度最小
B. 小球在A、B位置时,动能最大,加速度最大
C. 小球从A经O到B的过程中,回复力一直做正功
D. 小球从B到O的过程中,振动的能量不断增加
物块M与m叠放在一起,以O为平衡位置,在ab之间做简谐振动,两者始终保持相对静止,取向右为正方向,其振动的位移x随时间t的变化图像如下图,则下列说法正确的是(???? )
A. 在t1?T2时间内,物块m的速度和所受摩擦力都沿负方向,且都在增大
B. 从t1时刻开始计时,接下来T4内,两物块通过的路程为A
C. 在某段时间内,两物块速度增大时,加速度可能增大,也可能减小
D. 两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变
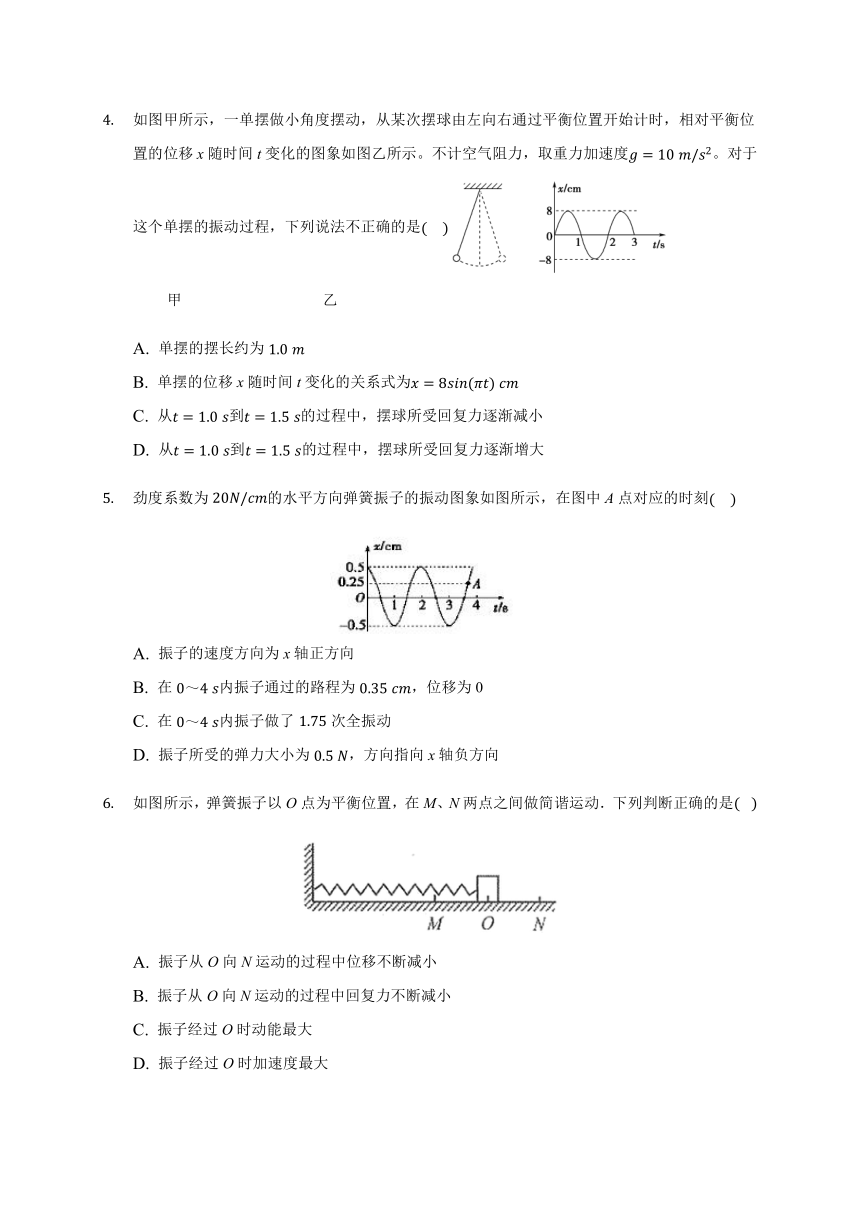
如图甲所示,一单摆做小角度摆动,从某次摆球由左向右通过平衡位置开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示。不计空气阻力,取重力加速度g=10?m/s2。对于这个单摆的振动过程,下列说法不正确的是(????)
? ? ? 甲? ? ? ? ? ? ? ? ? ? ? ? ?乙
A. 单摆的摆长约为1.0?m
B. 单摆的位移x随时间t变化的关系式为x=8sin(πt)?cm
C. 从t=1.0?s到t=1.5?s的过程中,摆球所受回复力逐渐减小
D. 从t=1.0?s到t=1.5?s的过程中,摆球所受回复力逐渐增大
劲度系数为20N/cm的水平方向弹簧振子的振动图象如图所示,在图中A点对应的时刻(????)
A. 振子的速度方向为x轴正方向
B. 在0~4?s内振子通过的路程为0.35?cm,位移为0
C. 在0~4?s内振子做了1.75次全振动
D. 振子所受的弹力大小为0.5?N,方向指向x轴负方向
如图所示,弹簧振子以O点为平衡位置,在M、N两点之间做简谐运动.下列判断正确的是(? )
A. 振子从O向N运动的过程中位移不断减小
B. 振子从O向N运动的过程中回复力不断减小
C. 振子经过O时动能最大
D. 振子经过O时加速度最大
一弹簧振子做简谐运动的图象如图所示,下列说法正确的
A. 振子的振幅为8cm
B. t=1s时振子的速度最大
C. t=2s时振子所受的回复力为零
D. 第2s内振子动能减小,势能增大
如图所示,一根用绝缘材料制成的劲度系数为k的轻弹簧,左端固定,右端与质量为m、带电量为+q的小球相连,静止在光滑、绝缘的水平面上.在施加一个场强为E、方向水平向右的匀强电场后,小球开始做简谐运动.那么(????)
A. 小球做简谐运动的振幅为2qE/k
B. 小球到达最右端时,弹簧的形变量为2qE/k
C. 运动过程中小球的机械能守恒
D. 运动过程中小球的电势能和弹簧的弹性势能的总量不变
光滑斜面上物块A被平行斜面的轻质弹簧拉住静止于O点,如图所示,现将A沿斜面拉到B点无初速释放,物块在BC范围内做简谐运动,则下列说法正确的是(????)
A. 在振动过程中,物块A机械能守恒
B. 物块A在C点时,弹簧性势能最小
C. 物块A在O点时,系统势能最小
D. 物块A在B点时机械能最大
如图所示,弹簧振子在B、C两点间做无摩擦的往复运动,O是振子的平衡位置。则振子从B向O运动过程中(????)
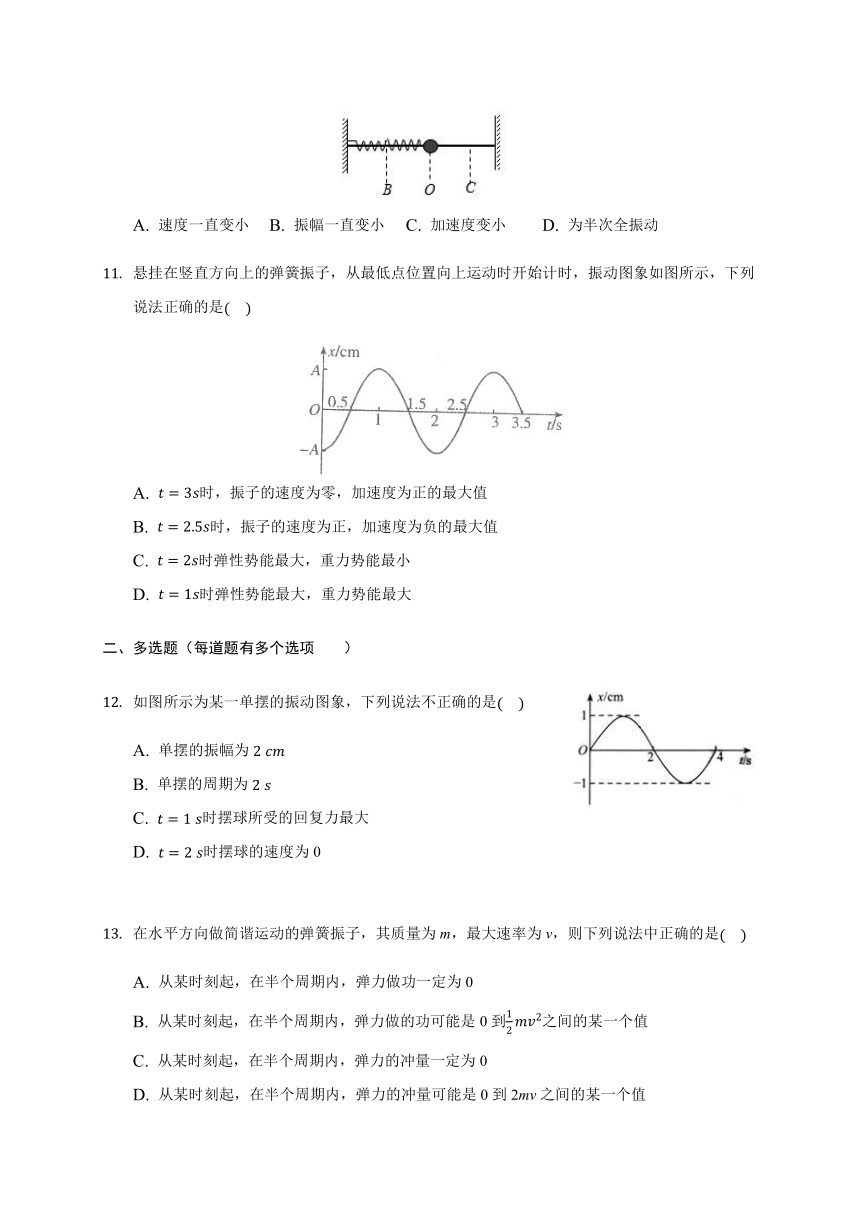
A. 速度一直变小 B. 振幅一直变小 C. 加速度变小 D. 为半次全振动
悬挂在竖直方向上的弹簧振子,从最低点位置向上运动时开始计时,振动图象如图所示,下列说法正确的是(????)
A. t=3s时,振子的速度为零,加速度为正的最大值
B. t=2.5s时,振子的速度为正,加速度为负的最大值
C. t=2s时弹性势能最大,重力势能最小
D. t=1s时弹性势能最大,重力势能最大
二、多选题(每道题有多个选项)
如图所示为某一单摆的振动图象,下列说法不正确的是(????)
A. 单摆的振幅为2?cm
B. 单摆的周期为2?s
C. t=1?s时摆球所受的回复力最大
D. t=2?s时摆球的速度为0
在水平方向做简谐运动的弹簧振子,其质量为m,最大速率为v,则下列说法中正确的是(????)
A. 从某时刻起,在半个周期内,弹力做功一定为0
B. 从某时刻起,在半个周期内,弹力做的功可能是0到12mv2之间的某一个值
C. 从某时刻起,在半个周期内,弹力的冲量一定为0
D. 从某时刻起,在半个周期内,弹力的冲量可能是0到2mv之间的某一个值
如图所示,在水平地面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,现将一个质量也为m的物体C从A的正上方一定高度处由静止释放,C和A相碰后立即粘在一起,之后在竖直方向做简谐运动。在简谐运动过程中,物体B对地面的最小弹力为,则以下说法正确的是(? )
A. 简谐运动的振幅为2.5mg/k
B. C和A相碰后立即减速向下运动
C. B对地面的最大弹力为5.5mg
D. 若C物体从更高的位置释放,碰后粘在一起向下运动速度最大的位置会更低
公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板.一段时间内货物在竖直方向的振动可视为简谐运动,周期为T.竖直向上为正方向,以某时刻为计时起点,其振动图象如图所示,则(????)
A. t=14T时,货物对车厢底板的压力最小
B. t=12T时,货物对车厢底板的压力最小
C. t=34T时,货物对车厢底板的压力最大
D. t=34T时,货物对车厢底板的压力最小
三、计算题(写清答题过程)
如图所示为一弹簧振子的振动图象,求:
(1)该振子简谐运动的表达式;
(2)在第2?s末到第3?s末这段时间内,弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?
(3)该振子在前100?s内的总位移是多少?路程是多少?
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动.B、C相距20cm.某时刻振子处于O点正向右运动.经过0.5s,振子首次到达B点.求:(取向右为正方向)
(1)振动的频率f和振幅A;
(2)振子在5.5s内通过的路程及位移?
(3)如果弹簧的k=100N/m,小球质量为0.5kg,则5.5s末小球的加速度大小和方向是多少?
弹簧振子以O点为平衡位置,在B、C两点之间做简谐运动,B、C相距10cm。t=0时刻振子处于B点,经过t1=2s,振子第一次到达C点。求:
(1)振子振动的周期;
(2)振子在t2=7s内通过的路程;
(3)振子在B点的加速度大小与它距O点3cm处的P点的加速度大小的比值。
答案和解析
1.【答案】C
【解析】解:A、由位移的表达式x=5sinπ4t(cm),可知质点做简谐运动的振幅为5cm。故A错误。
B、由位移的表达式读出圆频率ω=π4rad/s,则周期为T=2πω=8s。故B错误。
C、在t=4s时质点的位移x=5sinπ4tcm=5sinπ4×4cm=0cm,说明物体通过平衡位置,速度最大。故C正确。
D、在t=4s时质点通过平衡位置,加速度最小。故D错误。
2.【答案】A
3.【答案】D
【解答】
A.在t1?T2时间内,由于振子的位移为正,图线的斜率为负,物块m的速度和所受摩擦力都沿负方向,但速度在增大,而摩擦力在减小,故A错误;
B.从t1时刻开始计时,接下来T4内,两物块通过的路程不一定为A,故B错误;
C.在某段时间内,两物块速度增大时,位移减小,加速度一定减小,故C错误;
D.根据能量守恒两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变,故D正确。
4.【答案】C
【解答】
A.由公式T=2πLg=2s,代入得到L=1m.故A正确;
B.由振动图象读出周期T=2s,振幅A=8cm,由ω=2πT得到角频率ω=πrad/s,则单摆的位移x随时间t变化的关系式为Asinωt=8sin(πt)cm.故B正确;
CD.从t=1.0?s到t=1.5?s的过程中,摆球的位移增大,回复力增大.故D正确,C错误。
5.【答案】A
【解析】解:A、由“爬坡法”知振子的速度方向指向x轴的正方向,故A正确.
B、由于t=0时刻和t=4s时刻振子都在最大位移处,所以在0~4s内振子的位移为零,又由于振幅为0.5cm,在0~4s内振子完成了2次全振动,所以在这段时间内振子通过的路程为2×4×0.50cm=4cm,故B错误.
C、由图可看出,t=0、t=4s时刻振子的位移都是最大,且都在t轴的上方,在0~4s内经过两个周期,振子完成两次全振动,故C错误.
D、由图可知A在t轴上方,位移x=0.25cm,所以弹力F=?kx=?5N,即弹力大小为5N,方向指向x轴负方向,故D错误;
6.【答案】C
【解答】
AB.振子从O到N过程中远离平衡位置,位移增大,回复力增大,故AB错误;
CD.振子在经过O点时,速度最大,则动能最大,加速度为0,故C正确,D错误。
故选C。
7.【答案】C
【解答】
A.由图可知,振子的振幅为4cm,故A错误;
B.t=1s时振子的位移最大,速度为零,故B错误;
C.t=2s时振子在平衡位置位移为零,加速度为零,回复力为零,故C正确;
D.第2s内振子从最大位移处向平衡位置运动动,速度增大,动能增大,势能减小,故D错误;
8.【答案】B
【解答】
AB.小球做简谐运动,在平衡位置,有:kA=qE;
解得:A=qEk;
小球到达最右端时,弹簧的形变量为2倍振幅,即2A=2qEk,故A错误,B正确;
C.小球运动过程中有电场力做功,故机械能不守恒,故C错误;
D.小球运动过程中有电场力和弹簧弹力做功,故对于弹簧和小球系统,电势能和重力势能以及动能总量守恒,故D错误。
9.【答案】C
【解答】
A.在振动过程中,物块与弹簧构成的系统机械能守恒,物块A的机械能和弹簧的弹性势能相互转化,由于弹性势能是变化的,故物块A的机械能不守恒,故A错误;
B.当物块A被平行斜面的轻质弹簧拉住静止于O点时,物块A受到向上的弹力,所以弹簧处于伸长状态,结合简谐振动的对称性可知,物块在B点时弹簧的伸长量一定最长,而物块在C点时,弹簧可能处于原长状态,也可能处于压缩状态或伸长状态,可知在C点时,弹簧的弹性势能不一定最小,故B错误;
C.物块A和弹簧系统机械能守恒,在O点时,物块的动能最大,故势能最小,故C正确;
D.物块A和弹簧系统机械能守恒;物体在B点时,弹簧的伸长量最长,弹簧的弹性势能最大;物体A的机械能最小,故D错误。
10.【答案】C
11.【答案】C
【解答】
A.t=3s时,振子偏离平衡位置最远,速度为零,恢复力最大,加速度最大,方向指向平衡位置,故 A错误;
B.?t=2.5s时,振子位于平衡位置,速度最大,回复力和加速度均为零,故 B错误;
C.t=2s时,振子又回到最低点,在最低点弹簧的形变量最大,弹簧的弹性势能最大;根据重力势能的概
念可知,在最低点的重力势能最小,故C正确;
D.由于振子周期为2s,从最低点开始运动,所以t=1s时,振子在最高点,重力势能最大;由于弹簧振子
在坚直方向上振动在平衡位置处;kx=mg;设振子的振幅为A,则在最低点弹簧的形变量最大,为A+mgk,所以在最低点弹的弹性势能最大;故D错误;
12.【答案】ABD
13.【答案】AD
【解答】
AB、弹力做功的大小等于弹性势能的变化量;从某时刻起,在半个周期内,由于位移大小具有对称性,所以弹力做功为0,故A正确,B错误;
CD、对于简谐运动,经过半个周期后速度与之前的速度大小相等、方向相反;若初速度为v1,则末速度为?v1,故速度变化量为?2v1,若开始时在最大位移处,初速度为0,末速度也是0,所以速度变化量也是0,根据动量定理可知,弹力的冲量I=Δp=mΔv,所以弹力的冲量大小可能是0~2mv间的某一个值,故C错误,D正确.
14.【答案】AC
【解答】
A、物体B对地面的弹力最小时B受到的支持力最小,此时弹簧对B的作用力为拉力,对B:mg?kx1=12mg
则:kx1=0.5mg
再以A、C组成的整体为研究对象,则物体B对地面的弹力最小时弹簧对A的作用力也是拉力,此时A与C在最高点,则:2mg+kx1=2ma
可得:a=1.25g
由于简谐振动具有对称性,则A与C在最低点时加速度的大小也是1.25g,方向向上,此时:kx2?2mg=2ma
则:x2=9mg2k
A与C组成的整体受力平衡时:2mg=kx3
则:x3=2mgk
所以简谐振动的振幅:A=x2?x3=9mg2k?2mgk=2.5mgk,故A正确;
B、A与C碰撞后A与C整体受到的重力大于弹簧的弹力,所以它们将先向下做一段加速运动,故B错误;
C、A与C在最低点时B对地面得压力最大,受到的支持力也最大,则:F?mg?kx2=0
可得:F=5.5mg,故C正确;
D、A与C组成的整体受力平衡的平衡位置不变,所以当C物体从更高的位置释放,碰后粘在一起向下运动速度最大的位置也不变,故D错误。
15.【答案】AC
【解答】
A、在t=14T时刻,由图看出,货物的位移为正向最大,则货物的加速度为负向最大,即加速度向下最大,根据牛顿第二定律可知,货物受到的弹力最小,则货物对车厢底板的压力最小.故A正确.
B、在t=12T时刻,货物的位移为零,加速度为零,弹簧的弹力大小等于货物的重力,而在t=14T时刻,货物的弹力小于货物的重力,说明在t=12T时刻,货物的弹力不是最小,则货物对车厢底板的压力不是最小.故B错误.
C、D在t=34T时刻,由图看出,货物的位移为负向最大,则货物的加速度为正向最大,即加速度向上最大,根据牛顿第二定律可知,货物受到的弹力最大,则货物对车厢底板的压力最大.故C正确,D错误.
16.【答案】解:(1)由振动图象可得:A=5cm,T=4?s,φ=0
则ω=2πT=π2rad/s
故该振子做简谐运动的表达式为:x=5sinπ2t(cm)
(2)由图可知,在t=2?s时振子恰好通过平衡位置,此时加速度为零,随着时间的延续,位移值不断加大,加速度的值也变大,速度值不断变小,动能不断减小,弹性势能逐渐增大。当t=3s时,加速度的值达到最大,速度等于零,动能等于零,弹性势能达到最大值。
(3)振子经过一个周期位移为零,路程为5×4cm=20cm,前100?s刚好经过了25个周期,所以前100s振子位移x=0,振子路程s=20×25cm=500cm=5m。
17.【答案】解:(1)设振幅为A,由题意BC=2A=20?cm,
所以A=10?cm.
振子从O到B所用时间t=0.5?s,为周期T的14,
所以T=2.0?s;
f=1T=12?Hz.
(2)振子从平衡位置开始运动,在1个周期内通过的路程为4A,
故在t′=5.5?s=114T内通过的路程
s=114×4A=110?cm.
5.5?s内振子振动了114个周期,所以5.5?s末振子到达c点,所以它的位移大小为?10?cm.
(3)5.5?s末振子到达c点,所以它的位移大小为?10?cm,振子加速度a=?kxm=?100×(?0.1)0.5=20m/s2,方向与位移的方向相反,为向右.
18.【答案】解:(1)设振幅为A,由题意知:BC=2A=10cm
所以振幅为:A=5cm
振子从B到C所用时间:t1=2?s,为周期T的一半,
所以振子振动的周期:T=4?s
(2)振子在1个周期内通过的路程为4A,且t=0时刻振子处于B点,
故在t2=7s=74T内通过的路程为:s=7A=7×5cm=35cm
(3)根据牛顿第二定律,振子加速度:a=?kxm,a∝x.
所以振子在B点的加速度大小与它距O点3cm处的P点的加速度大小的比值为:
aB:aP=xB:xP=5:3
一、单选题(每道题只有一个正确答案)
某质点做简谐运动,其位移随时间变化的关系式为x=5sinπ4tcm,则下列关于质点运动的说法中正确的是(????)
A. 质点做简谐运动的振幅为10cm B. 质点做简谐运动的周期为4s
C. 在t=4s时质点的速度最大 D. 在t=4s时质点的加速度最大
把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它围绕平衡位置O在A、B间振动,如图所示,下列结论正确的是(????)
A. 小球在O位置时,动能最大,加速度最小
B. 小球在A、B位置时,动能最大,加速度最大
C. 小球从A经O到B的过程中,回复力一直做正功
D. 小球从B到O的过程中,振动的能量不断增加
物块M与m叠放在一起,以O为平衡位置,在ab之间做简谐振动,两者始终保持相对静止,取向右为正方向,其振动的位移x随时间t的变化图像如下图,则下列说法正确的是(???? )
A. 在t1?T2时间内,物块m的速度和所受摩擦力都沿负方向,且都在增大
B. 从t1时刻开始计时,接下来T4内,两物块通过的路程为A
C. 在某段时间内,两物块速度增大时,加速度可能增大,也可能减小
D. 两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变
如图甲所示,一单摆做小角度摆动,从某次摆球由左向右通过平衡位置开始计时,相对平衡位置的位移x随时间t变化的图象如图乙所示。不计空气阻力,取重力加速度g=10?m/s2。对于这个单摆的振动过程,下列说法不正确的是(????)
? ? ? 甲? ? ? ? ? ? ? ? ? ? ? ? ?乙
A. 单摆的摆长约为1.0?m
B. 单摆的位移x随时间t变化的关系式为x=8sin(πt)?cm
C. 从t=1.0?s到t=1.5?s的过程中,摆球所受回复力逐渐减小
D. 从t=1.0?s到t=1.5?s的过程中,摆球所受回复力逐渐增大
劲度系数为20N/cm的水平方向弹簧振子的振动图象如图所示,在图中A点对应的时刻(????)
A. 振子的速度方向为x轴正方向
B. 在0~4?s内振子通过的路程为0.35?cm,位移为0
C. 在0~4?s内振子做了1.75次全振动
D. 振子所受的弹力大小为0.5?N,方向指向x轴负方向
如图所示,弹簧振子以O点为平衡位置,在M、N两点之间做简谐运动.下列判断正确的是(? )
A. 振子从O向N运动的过程中位移不断减小
B. 振子从O向N运动的过程中回复力不断减小
C. 振子经过O时动能最大
D. 振子经过O时加速度最大
一弹簧振子做简谐运动的图象如图所示,下列说法正确的
A. 振子的振幅为8cm
B. t=1s时振子的速度最大
C. t=2s时振子所受的回复力为零
D. 第2s内振子动能减小,势能增大
如图所示,一根用绝缘材料制成的劲度系数为k的轻弹簧,左端固定,右端与质量为m、带电量为+q的小球相连,静止在光滑、绝缘的水平面上.在施加一个场强为E、方向水平向右的匀强电场后,小球开始做简谐运动.那么(????)
A. 小球做简谐运动的振幅为2qE/k
B. 小球到达最右端时,弹簧的形变量为2qE/k
C. 运动过程中小球的机械能守恒
D. 运动过程中小球的电势能和弹簧的弹性势能的总量不变
光滑斜面上物块A被平行斜面的轻质弹簧拉住静止于O点,如图所示,现将A沿斜面拉到B点无初速释放,物块在BC范围内做简谐运动,则下列说法正确的是(????)
A. 在振动过程中,物块A机械能守恒
B. 物块A在C点时,弹簧性势能最小
C. 物块A在O点时,系统势能最小
D. 物块A在B点时机械能最大
如图所示,弹簧振子在B、C两点间做无摩擦的往复运动,O是振子的平衡位置。则振子从B向O运动过程中(????)
A. 速度一直变小 B. 振幅一直变小 C. 加速度变小 D. 为半次全振动
悬挂在竖直方向上的弹簧振子,从最低点位置向上运动时开始计时,振动图象如图所示,下列说法正确的是(????)
A. t=3s时,振子的速度为零,加速度为正的最大值
B. t=2.5s时,振子的速度为正,加速度为负的最大值
C. t=2s时弹性势能最大,重力势能最小
D. t=1s时弹性势能最大,重力势能最大
二、多选题(每道题有多个选项)
如图所示为某一单摆的振动图象,下列说法不正确的是(????)
A. 单摆的振幅为2?cm
B. 单摆的周期为2?s
C. t=1?s时摆球所受的回复力最大
D. t=2?s时摆球的速度为0
在水平方向做简谐运动的弹簧振子,其质量为m,最大速率为v,则下列说法中正确的是(????)
A. 从某时刻起,在半个周期内,弹力做功一定为0
B. 从某时刻起,在半个周期内,弹力做的功可能是0到12mv2之间的某一个值
C. 从某时刻起,在半个周期内,弹力的冲量一定为0
D. 从某时刻起,在半个周期内,弹力的冲量可能是0到2mv之间的某一个值
如图所示,在水平地面上,有两个用轻质弹簧相连的物块A和B,它们的质量均为m,弹簧的劲度系数为k,现将一个质量也为m的物体C从A的正上方一定高度处由静止释放,C和A相碰后立即粘在一起,之后在竖直方向做简谐运动。在简谐运动过程中,物体B对地面的最小弹力为,则以下说法正确的是(? )
A. 简谐运动的振幅为2.5mg/k
B. C和A相碰后立即减速向下运动
C. B对地面的最大弹力为5.5mg
D. 若C物体从更高的位置释放,碰后粘在一起向下运动速度最大的位置会更低
公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板.一段时间内货物在竖直方向的振动可视为简谐运动,周期为T.竖直向上为正方向,以某时刻为计时起点,其振动图象如图所示,则(????)
A. t=14T时,货物对车厢底板的压力最小
B. t=12T时,货物对车厢底板的压力最小
C. t=34T时,货物对车厢底板的压力最大
D. t=34T时,货物对车厢底板的压力最小
三、计算题(写清答题过程)
如图所示为一弹簧振子的振动图象,求:
(1)该振子简谐运动的表达式;
(2)在第2?s末到第3?s末这段时间内,弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?
(3)该振子在前100?s内的总位移是多少?路程是多少?
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动.B、C相距20cm.某时刻振子处于O点正向右运动.经过0.5s,振子首次到达B点.求:(取向右为正方向)
(1)振动的频率f和振幅A;
(2)振子在5.5s内通过的路程及位移?
(3)如果弹簧的k=100N/m,小球质量为0.5kg,则5.5s末小球的加速度大小和方向是多少?
弹簧振子以O点为平衡位置,在B、C两点之间做简谐运动,B、C相距10cm。t=0时刻振子处于B点,经过t1=2s,振子第一次到达C点。求:
(1)振子振动的周期;
(2)振子在t2=7s内通过的路程;
(3)振子在B点的加速度大小与它距O点3cm处的P点的加速度大小的比值。
答案和解析
1.【答案】C
【解析】解:A、由位移的表达式x=5sinπ4t(cm),可知质点做简谐运动的振幅为5cm。故A错误。
B、由位移的表达式读出圆频率ω=π4rad/s,则周期为T=2πω=8s。故B错误。
C、在t=4s时质点的位移x=5sinπ4tcm=5sinπ4×4cm=0cm,说明物体通过平衡位置,速度最大。故C正确。
D、在t=4s时质点通过平衡位置,加速度最小。故D错误。
2.【答案】A
3.【答案】D
【解答】
A.在t1?T2时间内,由于振子的位移为正,图线的斜率为负,物块m的速度和所受摩擦力都沿负方向,但速度在增大,而摩擦力在减小,故A错误;
B.从t1时刻开始计时,接下来T4内,两物块通过的路程不一定为A,故B错误;
C.在某段时间内,两物块速度增大时,位移减小,加速度一定减小,故C错误;
D.根据能量守恒两物块运动到最大位移处时,若轻轻取走m,则M的振幅不变,故D正确。
4.【答案】C
【解答】
A.由公式T=2πLg=2s,代入得到L=1m.故A正确;
B.由振动图象读出周期T=2s,振幅A=8cm,由ω=2πT得到角频率ω=πrad/s,则单摆的位移x随时间t变化的关系式为Asinωt=8sin(πt)cm.故B正确;
CD.从t=1.0?s到t=1.5?s的过程中,摆球的位移增大,回复力增大.故D正确,C错误。
5.【答案】A
【解析】解:A、由“爬坡法”知振子的速度方向指向x轴的正方向,故A正确.
B、由于t=0时刻和t=4s时刻振子都在最大位移处,所以在0~4s内振子的位移为零,又由于振幅为0.5cm,在0~4s内振子完成了2次全振动,所以在这段时间内振子通过的路程为2×4×0.50cm=4cm,故B错误.
C、由图可看出,t=0、t=4s时刻振子的位移都是最大,且都在t轴的上方,在0~4s内经过两个周期,振子完成两次全振动,故C错误.
D、由图可知A在t轴上方,位移x=0.25cm,所以弹力F=?kx=?5N,即弹力大小为5N,方向指向x轴负方向,故D错误;
6.【答案】C
【解答】
AB.振子从O到N过程中远离平衡位置,位移增大,回复力增大,故AB错误;
CD.振子在经过O点时,速度最大,则动能最大,加速度为0,故C正确,D错误。
故选C。
7.【答案】C
【解答】
A.由图可知,振子的振幅为4cm,故A错误;
B.t=1s时振子的位移最大,速度为零,故B错误;
C.t=2s时振子在平衡位置位移为零,加速度为零,回复力为零,故C正确;
D.第2s内振子从最大位移处向平衡位置运动动,速度增大,动能增大,势能减小,故D错误;
8.【答案】B
【解答】
AB.小球做简谐运动,在平衡位置,有:kA=qE;
解得:A=qEk;
小球到达最右端时,弹簧的形变量为2倍振幅,即2A=2qEk,故A错误,B正确;
C.小球运动过程中有电场力做功,故机械能不守恒,故C错误;
D.小球运动过程中有电场力和弹簧弹力做功,故对于弹簧和小球系统,电势能和重力势能以及动能总量守恒,故D错误。
9.【答案】C
【解答】
A.在振动过程中,物块与弹簧构成的系统机械能守恒,物块A的机械能和弹簧的弹性势能相互转化,由于弹性势能是变化的,故物块A的机械能不守恒,故A错误;
B.当物块A被平行斜面的轻质弹簧拉住静止于O点时,物块A受到向上的弹力,所以弹簧处于伸长状态,结合简谐振动的对称性可知,物块在B点时弹簧的伸长量一定最长,而物块在C点时,弹簧可能处于原长状态,也可能处于压缩状态或伸长状态,可知在C点时,弹簧的弹性势能不一定最小,故B错误;
C.物块A和弹簧系统机械能守恒,在O点时,物块的动能最大,故势能最小,故C正确;
D.物块A和弹簧系统机械能守恒;物体在B点时,弹簧的伸长量最长,弹簧的弹性势能最大;物体A的机械能最小,故D错误。
10.【答案】C
11.【答案】C
【解答】
A.t=3s时,振子偏离平衡位置最远,速度为零,恢复力最大,加速度最大,方向指向平衡位置,故 A错误;
B.?t=2.5s时,振子位于平衡位置,速度最大,回复力和加速度均为零,故 B错误;
C.t=2s时,振子又回到最低点,在最低点弹簧的形变量最大,弹簧的弹性势能最大;根据重力势能的概
念可知,在最低点的重力势能最小,故C正确;
D.由于振子周期为2s,从最低点开始运动,所以t=1s时,振子在最高点,重力势能最大;由于弹簧振子
在坚直方向上振动在平衡位置处;kx=mg;设振子的振幅为A,则在最低点弹簧的形变量最大,为A+mgk,所以在最低点弹的弹性势能最大;故D错误;
12.【答案】ABD
13.【答案】AD
【解答】
AB、弹力做功的大小等于弹性势能的变化量;从某时刻起,在半个周期内,由于位移大小具有对称性,所以弹力做功为0,故A正确,B错误;
CD、对于简谐运动,经过半个周期后速度与之前的速度大小相等、方向相反;若初速度为v1,则末速度为?v1,故速度变化量为?2v1,若开始时在最大位移处,初速度为0,末速度也是0,所以速度变化量也是0,根据动量定理可知,弹力的冲量I=Δp=mΔv,所以弹力的冲量大小可能是0~2mv间的某一个值,故C错误,D正确.
14.【答案】AC
【解答】
A、物体B对地面的弹力最小时B受到的支持力最小,此时弹簧对B的作用力为拉力,对B:mg?kx1=12mg
则:kx1=0.5mg
再以A、C组成的整体为研究对象,则物体B对地面的弹力最小时弹簧对A的作用力也是拉力,此时A与C在最高点,则:2mg+kx1=2ma
可得:a=1.25g
由于简谐振动具有对称性,则A与C在最低点时加速度的大小也是1.25g,方向向上,此时:kx2?2mg=2ma
则:x2=9mg2k
A与C组成的整体受力平衡时:2mg=kx3
则:x3=2mgk
所以简谐振动的振幅:A=x2?x3=9mg2k?2mgk=2.5mgk,故A正确;
B、A与C碰撞后A与C整体受到的重力大于弹簧的弹力,所以它们将先向下做一段加速运动,故B错误;
C、A与C在最低点时B对地面得压力最大,受到的支持力也最大,则:F?mg?kx2=0
可得:F=5.5mg,故C正确;
D、A与C组成的整体受力平衡的平衡位置不变,所以当C物体从更高的位置释放,碰后粘在一起向下运动速度最大的位置也不变,故D错误。
15.【答案】AC
【解答】
A、在t=14T时刻,由图看出,货物的位移为正向最大,则货物的加速度为负向最大,即加速度向下最大,根据牛顿第二定律可知,货物受到的弹力最小,则货物对车厢底板的压力最小.故A正确.
B、在t=12T时刻,货物的位移为零,加速度为零,弹簧的弹力大小等于货物的重力,而在t=14T时刻,货物的弹力小于货物的重力,说明在t=12T时刻,货物的弹力不是最小,则货物对车厢底板的压力不是最小.故B错误.
C、D在t=34T时刻,由图看出,货物的位移为负向最大,则货物的加速度为正向最大,即加速度向上最大,根据牛顿第二定律可知,货物受到的弹力最大,则货物对车厢底板的压力最大.故C正确,D错误.
16.【答案】解:(1)由振动图象可得:A=5cm,T=4?s,φ=0
则ω=2πT=π2rad/s
故该振子做简谐运动的表达式为:x=5sinπ2t(cm)
(2)由图可知,在t=2?s时振子恰好通过平衡位置,此时加速度为零,随着时间的延续,位移值不断加大,加速度的值也变大,速度值不断变小,动能不断减小,弹性势能逐渐增大。当t=3s时,加速度的值达到最大,速度等于零,动能等于零,弹性势能达到最大值。
(3)振子经过一个周期位移为零,路程为5×4cm=20cm,前100?s刚好经过了25个周期,所以前100s振子位移x=0,振子路程s=20×25cm=500cm=5m。
17.【答案】解:(1)设振幅为A,由题意BC=2A=20?cm,
所以A=10?cm.
振子从O到B所用时间t=0.5?s,为周期T的14,
所以T=2.0?s;
f=1T=12?Hz.
(2)振子从平衡位置开始运动,在1个周期内通过的路程为4A,
故在t′=5.5?s=114T内通过的路程
s=114×4A=110?cm.
5.5?s内振子振动了114个周期,所以5.5?s末振子到达c点,所以它的位移大小为?10?cm.
(3)5.5?s末振子到达c点,所以它的位移大小为?10?cm,振子加速度a=?kxm=?100×(?0.1)0.5=20m/s2,方向与位移的方向相反,为向右.
18.【答案】解:(1)设振幅为A,由题意知:BC=2A=10cm
所以振幅为:A=5cm
振子从B到C所用时间:t1=2?s,为周期T的一半,
所以振子振动的周期:T=4?s
(2)振子在1个周期内通过的路程为4A,且t=0时刻振子处于B点,
故在t2=7s=74T内通过的路程为:s=7A=7×5cm=35cm
(3)根据牛顿第二定律,振子加速度:a=?kxm,a∝x.
所以振子在B点的加速度大小与它距O点3cm处的P点的加速度大小的比值为:
aB:aP=xB:xP=5:3
