4.4 实验:用双缝干涉测量光的波长同步练习 (word版含答案)
文档属性
| 名称 | 4.4 实验:用双缝干涉测量光的波长同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 321.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-25 16:45:22 | ||
图片预览



文档简介
实验:用双缝干涉测量光的波长练习
一、单选题
有同学在重复杨氏双缝干涉实验中,用白光照射双缝前的单缝时,在光屏上呈现出彩色条纹.现在这位同学又进行了如下的探究,仍用白光照射双缝前的单缝,然后在双缝处用一个蓝色玻璃片挡住其中的一缝,用一个红色玻璃片挡住另一缝后(????)
A. 在光屏上出现红蓝相间的干涉条纹
B. 在光屏上出现明暗相间的蓝色干涉条纹
C. 在光屏上出现明暗相间的红色干涉条纹
D. 在光屏看不到干涉条纹
用杨氏双缝实验演示光的干涉,不影响条纹位置的因素是(????)
A. 光的强度 B. 光的波长
C. 屏与狭缝的距离 D. 两狭缝间的距离
某同学用某种单色光做双缝干涉实验时,发现条纹太密难以测量,可以采用的改善办法是(????)
A. 增大双缝间距
B. 增大双缝到屏的距离
C. 增大双缝到单缝的距离
D. 改用波长较短的光(如紫光)作为入射光
用单色光做双缝干涉实验,下述说法中正确的是(????)
A. 相邻干涉条纹之间的距离不相等
B. 中央明条纹宽度是两边明条纹宽度的2倍
C. 屏与双缝之间距离减小,则屏上条纹间的距离增大
D. 在实验装置不变的情况下,红光的条纹间距小于蓝光的条纹间距
在光的双缝干涉实验中,光屏上出现的条纹情况是(????)
A. 中心处的明条纹宽度比两侧的明条纹宽度大
B. 各种不同色光的明条纹间距一样大
C. 在相同装置中红光的明条纹间距比紫光的明条纹间距大
D. 对于同种色光,光屏离双缝距离越近明条纹的间距越大
某次实验中,测得第一级明条纹和第三级明条纹相距4.0×10?2m,若双缝片间距为0.1mm,缝到屏的距离为l=4.0?m,则光波的波长为(??? )
A. 8.0×10?8m B. 5.0×10?7m C. 1.5×10?8m D. 1.0×10?7m
杨氏双缝干涉实验中,下列说法正确的是(n为自然数,λ为光波波长)(??? )
①在距双缝的路程差相等的点形成暗条纹
②在距双缝的路程差为nλ的点形成亮条纹
③在距双缝路程差为nλ2的点形成亮条纹
④在距双缝路程差为2n+1λ2的点形成暗条
A. ①② B. ②③ C. ③④ D. ②④
如图是双缝干涉的实验装置示意图,其中S是单缝,S1、S2为双缝,P为光屏,实验时从左侧入射平行光,判断下述说法中正确的是(??? )
A. 把入射平行光由绿光换成紫光后,屏上干涉条纹中相邻两条明纹间的距离就变大
B. 把入射光由绿光换成红光后,屏上干涉条纹中相邻两条明纹间的距离就变大
C. 入射光为单色平行光,当双缝S1、S2之间的距离变小时,屏上干涉条纹中相邻两条明纹间的距离变小
D. 若入射光为白光,将缝S1左边加红色滤光片(只透过红光),将缝S2左边加蓝色滤光片(只透过蓝光),则屏上出现彩色干涉条纹
1801年,托马斯·杨(图甲)用双缝干涉实验研究了光波的性质,证实了光的波动性,在光的波动说中具有重要的地位和意义。如图乙所示为双缝干涉实验装置,单缝S在双缝S1、S2的中心对称轴上,实验中在屏上P点刚好得到的是中央亮纹上方第3级亮纹,现要使P处出现中央亮纹上方第4级亮纹,可采取的措施有(????)
A. 适当增大屏到双缝的距离 B. 适当增大单缝到双缝的距离
C. 换用频率更低的单色光 D. 换用波长更短的单色光
二、多选题
在双缝干涉实验中,用蓝色激光照射在双缝上,在缝后的屏幕上显示出干涉图样。若要增大干涉图样中两相邻亮条纹的间距,可选用的方法是
A. 增大双缝间距 B. 改用红色激光
C. 增大屏幕与双缝的间距 D. 增大光源与双缝的间距
如图所示,在利用双缝干涉测量光的波长的实验中,单缝S0、双缝中点O、屏上的P0点均位于双缝S1和S2的中垂线上,屏上P点处是P0上方的第3条亮条纹(不包括P0点处的亮条纹)的中心。已知入射光在真空中的波长为λ,真空中的光速为c,双缝S1与S2之间距离为d,双缝到屏的距离为L,若整个装置处于真空中,则下列说法正确的是(????)
A. 来自双缝S1和S2的光传播到P点处的时间差为3λc
B. 屏上P点和P0点之间仅能观察到两条暗条纹
C. 仅将单缝S0向左(保持S0在双缝的中垂线上)移动的过程中,P点处能观察到暗条纹
D. 仅将屏向右(保持P0在双缝的中垂线上)移动的过程中,P点处能观察到暗条纹
如图甲所示,在平静的水面下深h处有一个点光源s,它发出的两种不同颜色的a光和b光在水面上形成了一个有光线射出的圆形区域,该区域的中间为由ab两种单色光所构成的复色光圆形区域周围为环状区域,且为a光的颜色(见图乙)设b光的折射率为nb,则下列说法正确的是(????)
A. 在水中,a光的波长比b光小
B. 在水中,a光的传播速度比b光大
C. 复色光圆形区域的面积为S=π?2nb2?1
D. 在同一装置的杨氏双缝干涉实验中,a光的干涉条纹比b光窄
下列说法中正确的是(????)
A. 变化的电场一定产生变化的磁场
B. 电磁波是横波
C. 紫外线的频率比红外线的频率大
D. 障碍物的尺寸比光的波长大时,不能发生光的衍射现象
E. 在“双缝干涉实验”中,其它条件不变,若双缝间距越大,屏上相邻亮条纹间距越小
三、实验题
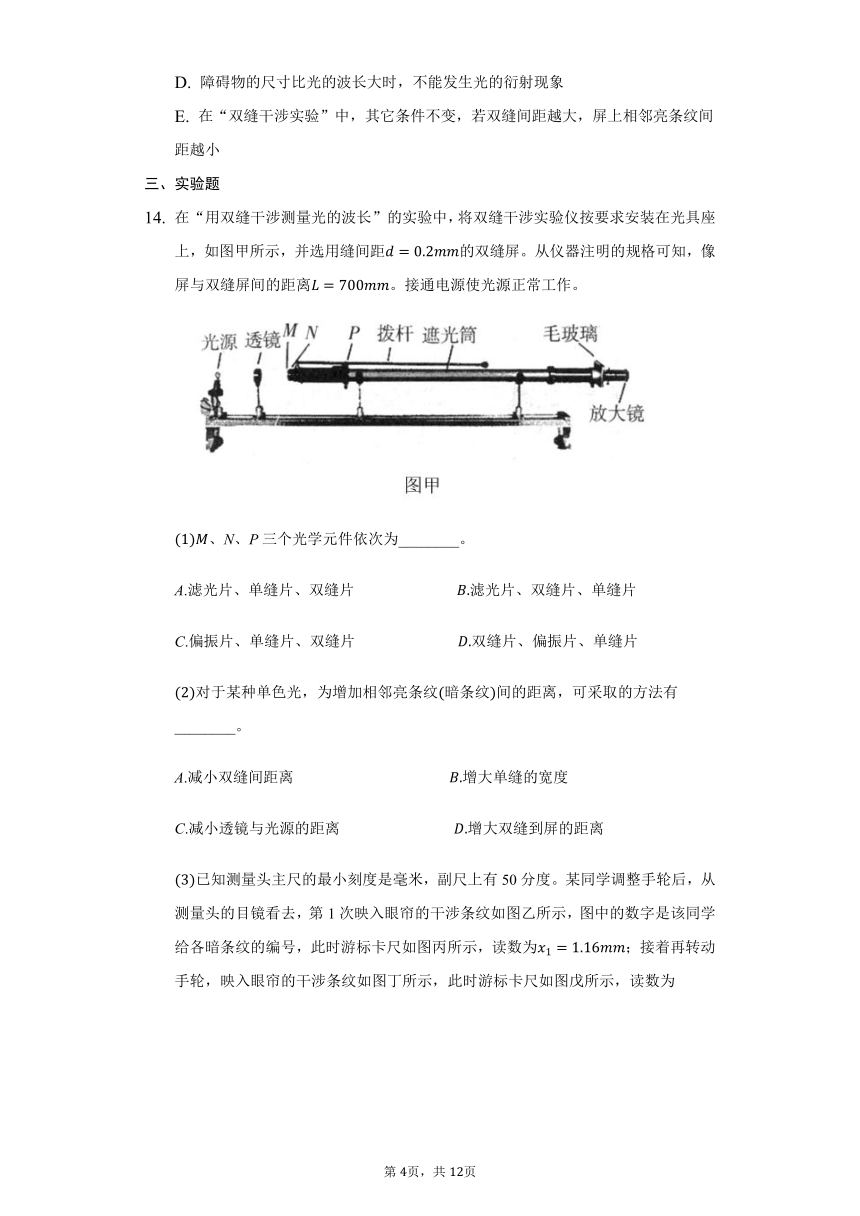
在“用双缝干涉测量光的波长”的实验中,将双缝干涉实验仪按要求安装在光具座上,如图甲所示,并选用缝间距d=0.2mm的双缝屏。从仪器注明的规格可知,像屏与双缝屏间的距离L=700mm。接通电源使光源正常工作。
(1)M、N、P三个光学元件依次为________。
A.滤光片、单缝片、双缝片????????????????????????? B.滤光片、双缝片、单缝片
C.偏振片、单缝片、双缝片????????????????????????? D.双缝片、偏振片、单缝片
(2)对于某种单色光,为增加相邻亮条纹(暗条纹)间的距离,可采取的方法有________。
A.减小双缝间距离??????????????????????????????????????? B.增大单缝的宽度
C.减小透镜与光源的距离???????????????????????????? D.增大双缝到屏的距离
(3)已知测量头主尺的最小刻度是毫米,副尺上有50分度。某同学调整手轮后,从测量头的目镜看去,第1次映入眼帘的干涉条纹如图乙所示,图中的数字是该同学给各暗条纹的编号,此时游标卡尺如图丙所示,读数为x1=1.16mm;接着再转动手轮,映入眼帘的干涉条纹如图丁所示,此时游标卡尺如图戊所示,读数为x2=________mm。
(4)利用上述测量结果,经计算可得两个相邻亮条纹(或暗条纹)的距离Δx,进而计算得到这种色光的彼长λ=________nm。
(5)一同学通过测量头的目镜观察单色光的干涉图样时,发现里面的亮条纹与分划板竖线未对齐,如图己所示。若要使两者对齐,该同学应________。
A.仅左右转动透镜??????????????????????????????????????? B.仅旋转滤光片
C.仅拨动拨杆?????????????????????????????????????????????? D.仅旋转测量头
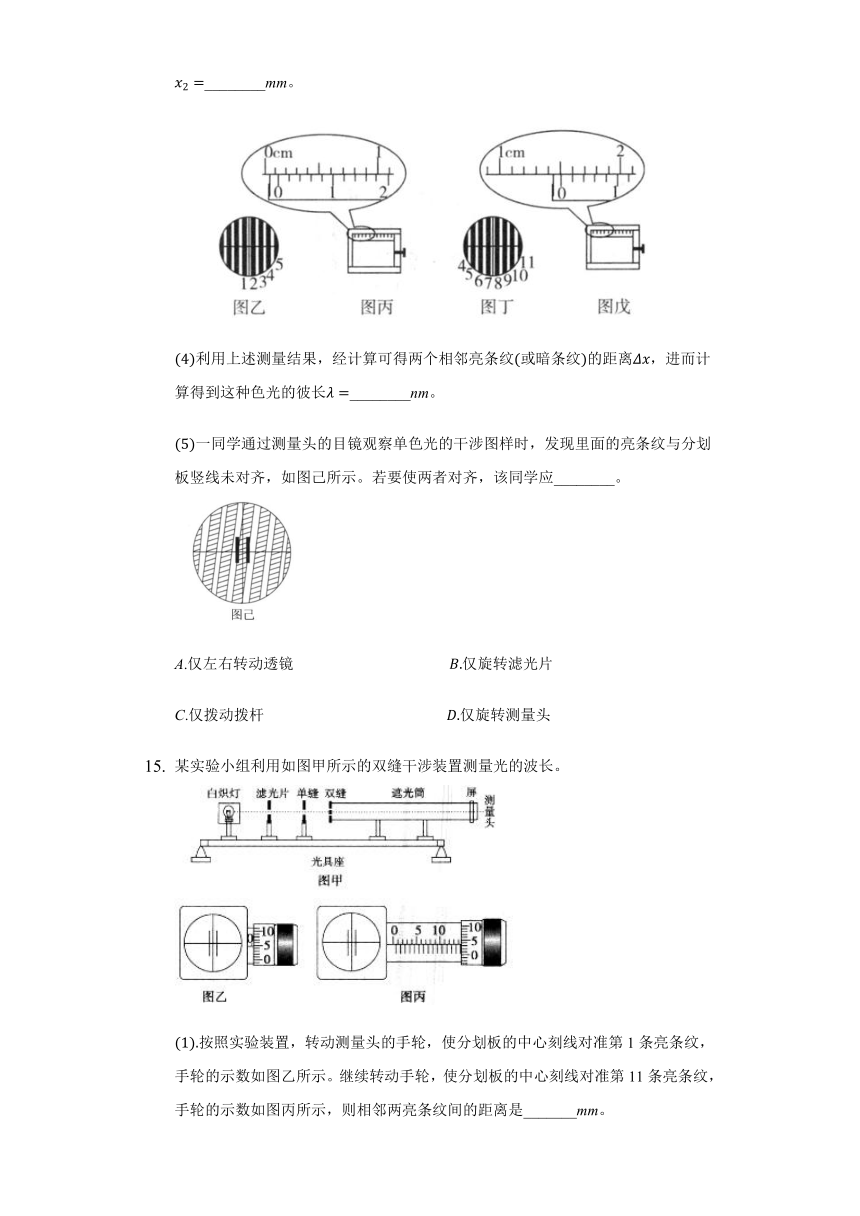
某实验小组利用如图甲所示的双缝干涉装置测量光的波长。
(1).按照实验装置,转动测量头的手轮,使分划板的中心刻线对准第1条亮条纹,手轮的示数如图乙所示。继续转动手轮,使分划板的中心刻线对准第11条亮条纹,手轮的示数如图丙所示,则相邻两亮条纹间的距离是_______mm。
(2).已知单缝与双缝的距离L1=60mm,双缝与光屏的距离L2=700mm,单缝宽d1=0.10mm,双缝间距d2=0.25mm。则待测光的波长是_____nm(保留三位有效数字)。
利用所学物理知识解答问题:
(1)如图甲所示是用双缝干涉测光波波长的实验设备示意图,图中①是光源,②是滤光片,③是单缝,④是双缝,⑤是光屏。下列操作能增大光屏上相邻两条亮纹之间距离的是______
A.增大③和④之间的距离
B.增大④和⑤之间的距离
C.将绿色滤光片改成红色滤光片
D.增大双缝之间的距离
(2)如果将灯泡换成激光光源,该实验照样可以完成,这时可以去掉的部件是______(填数字代号)。
(3)转动测量头的手轮,使分划板中心刻线对准第1条亮纹,读出手轮的读数如图乙所示。继续转动手轮,使分划板中心刻线对准第10条亮纹,读出手轮的读数如图丙所示。则相邻两亮条纹的间距是______mm。
(4)如果已经量得双缝的间距是0.30mm、双缝和光屏之间的距离是900mm,则待测光的波长是______m.(取三位有效数字)
利用双缝干涉测定光的波长的实验中,双缝间距d=0.4mm,双缝到光屏间的距离l=0.5m,用某种单色光照射双缝得到干涉条纹如图所示,分划板在图中A、B位置时游标卡尺读数也如图中所给出,则:
(1)分划板在图中A、B位置时游标卡尺读数分别为xA=______mm,xB=______mm,相邻两条亮条纹中心之间的距离为△x=______mm。
(2)该单色光的波长λ=______m。
(3)若增大双缝的间距,其他条件保持不变,则得到的干涉条纹间距将______(填“变大”“不变”或“变小”);若改用频率较高的单色光照射,其他条件保持不变,则得到的干涉条纹间距将______(填“变大”“不变”或“变小”)。
在“用双缝干涉测量光的波长”的实验中,将双缝干涉实验仪按要求安装在光具座上(如图所示),并选用缝间距d=0.2?mm的双缝屏.从仪器注明的规格可知,像屏与双缝屏间的距离L=700?mm.然后,接通电源使光源正常工作.
(1)已知测量头主尺的最小刻度是毫米,副尺上有50分度.某同学调整手轮后,从测量头的目镜看去,第1次映入眼帘的干涉条纹如图甲所示,图中的数字是该同学给各暗条纹的编号,此时图乙中游标卡尺上的读数x1=1.16?mm;接着再转动手轮,映入眼帘的干涉条纹如图丙所示,此时图丁中游标卡尺上的读数x2=____________?mm;
(2)利用上述测量结果,经计算可得两个相邻亮条纹(或暗条纹)间的距离Δx=________?mm;这种色光的波长λ=________?nm.
答案和解析
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】D
【解答】
由于想将原来的第3级亮纹变成第四级亮纹,说明两相邻亮条纹的距离变短了,根据公式Δx=Ldλ,L为屏到双缝的距离,d为双缝之间的距离,λ为波长,可知换用波长更短的单色光可以实现目的。
故答案为D。
10.【答案】BC
【解答】
根据双缝干涉条纹间距公式Δx=Ldλ知,增大入射光的波长,减小双缝间距,以及增大屏与双缝的距离,可以增大条纹的间距,由于红光的波长大于蓝光的波长,可知改用红色激光可以增大条纹间距,故BC正确。
11.【答案】AD
【解析】解:A、根据题意可知,P点到双缝的光程差为△x=3λ,
所以来自双缝S1和S2的光传播到P点处的时间差为△t=3λc,故A正确;
B、由题意可知,屏上P点和P0点之间仅能观察到三条暗条纹,故B错误;
C、仅将单缝S0向左移动的过程中,光源到P点的光程差不变,仍然为3λ,所以P点还是亮条纹,故C错误;
D、仅将屏向右移动的过程中,P点到光源的光程差逐渐发生变化,当P到光源的光程差为半个波长的奇数倍时,P点观察到暗条纹,故D正确。
12.【答案】BC
【解答】
AB.a光在水面上形成的圆形亮斑面积较大,知a光的临界角较大,根据sinC=1n,知a光的折射率较小,再由v=cn=λf,可知,在水中,a光的波长比b光大,a光的传播速度比b光大,故A错误,B正确;
C.依据sinC=1n,结合几何关系,可知,r?2+r2=1nb,而复色光圆形区域的面积为S=πr2=π?2nb2?1,故C正确;
D.a光的折射率小,波长长,根据双缝干涉条纹与波长成正比,可知相同条件下,a光干涉条纹比b光宽,故E错误。
13.【答案】BCE
【解析】解:A、根据麦克斯韦电磁场理论,可知变化的电场产生磁场,均匀变化的电场产生稳定的磁场,故A错误;
B、光的偏振现象说明电磁波是横波,故B正确;
C、根据电磁波谱可知紫外线的频率比红外线的频率大,故C正确;
D、障碍物的尺寸比光的波长大时,能发生光的衍射现象,只不过衍射现象不会很明显,故D错误;
E、在“双缝干涉实验”中,据△x=Ldλ,可知其它条件不变,若双缝间距越大,屏上相邻亮条纹间距越小,故E正确。
14.【答案】(1)A;
(2)AD;
(3)15.02?;
(4)660;
(5)D。
【解答】(1)双缝干涉实验是让单色光通过双缝在光屏上形成干涉图样,所以让白炽灯光通过滤光片形成单色光,再经过单缝形成线光源,再通过双缝形成干涉条纹。故自光源起合理的顺序是滤光片、单缝片、双缝片,选A。
(2)根据相邻亮条纹间的距离为Δx=Ldλ,为增加相邻亮条纹(暗条纹)间的距离,可减小双缝间距离或增大双缝到屏的距离,AD正确,BC错误。
(3)题图戊中,游标卡尺的主尺读数为15mm,游标读数为0.02mm×1=0.02mm,所以最终读数为x2=15.02mm。
(4)两个相邻亮条纹(或暗条纹)间的距离,
根据,得。
(5)旋转测量头,分划板竖线随之旋转,可使分划板竖线与亮条纹对齐,故选D。
15.【答案】(1)1.449;(2)518
16.【答案】(1)BC;(2)②③;(3)1.61;(4)5.37×10?7
【解答】
(1)根据Δx=Ldλ知,为增大相邻亮纹(暗纹)间的距离,可采取增大双缝到光屏的距离、减小双缝间距离、或增大入射光的波长,而单缝与双缝间距不会影响条纹间距。故BC正确,AD错误。
故选BC。
(2)将灯泡换成激光光源,激光的单色性好,不需要滤光片与单缝,即为②与③。
(3)图乙中固定刻度读数为0.0mm,可动刻度读数为0.01mm×4.5=0.045mm,所以最终读数x1=0.045mm。
图丙中固定刻度读数为14.5mm,可动刻度读数为:0.01mm×3.5=0.035mm,所以最终读数x10=14.535mm。
根据Δx=14.535?0.04510?1mm=1.61mm;
(4)相邻干涉条纹的间距Δx=1.61mm=1.61×10?3m;
由Δx=Ldλ得λ=Δx?dL=1.61×10?3×0.3×10?30.9m=5.37×10?7m。
17.【答案】(1)11.1,15.6,0.75;(2)6×10?7;(3)变小,变小。
【解析】解:(1)十等分的游标卡尺,其精确度为0.1mm,
A位置游标卡尺的读数为:11mm+0.1×1mm=11.1mm;
B位置游标卡尺的读数为:15mm+0.1×6mm=15.6mm;
相邻两条纹间距:△x=xB?xA6=0.75mm。
(2)根据△x=Ldλ知波长的表达式为:λ=△x?dl
解得波长为:λ=0.75×10?3×0.4×10?30.5m=6×10?7m。
(3)根据△x=Ldλ知,增大双缝的间距,其他条件保持不变,则得到的干涉条纹间距变小;频率变高,波长变小,则干涉条纹的间距变小。
18.【答案】(1)15.02;(2)2.31;660
【解答】
(1)图游标卡尺的主尺读数为15mm,游标读数为0.02×1=0.02mm,所以最终读数为15.02mm;
(2)两个相邻明纹(或暗纹)间的距离Δx=x2?x1n=15.02?1.166mm=2.31mm
根据Δx=Ldλ得,λ=ΔxdL=2.31×10?3×0.2×10?30.7m=6.60×10?7m=660nm.
故答案为:(1)15.02;(2)2.31;660。
一、单选题
有同学在重复杨氏双缝干涉实验中,用白光照射双缝前的单缝时,在光屏上呈现出彩色条纹.现在这位同学又进行了如下的探究,仍用白光照射双缝前的单缝,然后在双缝处用一个蓝色玻璃片挡住其中的一缝,用一个红色玻璃片挡住另一缝后(????)
A. 在光屏上出现红蓝相间的干涉条纹
B. 在光屏上出现明暗相间的蓝色干涉条纹
C. 在光屏上出现明暗相间的红色干涉条纹
D. 在光屏看不到干涉条纹
用杨氏双缝实验演示光的干涉,不影响条纹位置的因素是(????)
A. 光的强度 B. 光的波长
C. 屏与狭缝的距离 D. 两狭缝间的距离
某同学用某种单色光做双缝干涉实验时,发现条纹太密难以测量,可以采用的改善办法是(????)
A. 增大双缝间距
B. 增大双缝到屏的距离
C. 增大双缝到单缝的距离
D. 改用波长较短的光(如紫光)作为入射光
用单色光做双缝干涉实验,下述说法中正确的是(????)
A. 相邻干涉条纹之间的距离不相等
B. 中央明条纹宽度是两边明条纹宽度的2倍
C. 屏与双缝之间距离减小,则屏上条纹间的距离增大
D. 在实验装置不变的情况下,红光的条纹间距小于蓝光的条纹间距
在光的双缝干涉实验中,光屏上出现的条纹情况是(????)
A. 中心处的明条纹宽度比两侧的明条纹宽度大
B. 各种不同色光的明条纹间距一样大
C. 在相同装置中红光的明条纹间距比紫光的明条纹间距大
D. 对于同种色光,光屏离双缝距离越近明条纹的间距越大
某次实验中,测得第一级明条纹和第三级明条纹相距4.0×10?2m,若双缝片间距为0.1mm,缝到屏的距离为l=4.0?m,则光波的波长为(??? )
A. 8.0×10?8m B. 5.0×10?7m C. 1.5×10?8m D. 1.0×10?7m
杨氏双缝干涉实验中,下列说法正确的是(n为自然数,λ为光波波长)(??? )
①在距双缝的路程差相等的点形成暗条纹
②在距双缝的路程差为nλ的点形成亮条纹
③在距双缝路程差为nλ2的点形成亮条纹
④在距双缝路程差为2n+1λ2的点形成暗条
A. ①② B. ②③ C. ③④ D. ②④
如图是双缝干涉的实验装置示意图,其中S是单缝,S1、S2为双缝,P为光屏,实验时从左侧入射平行光,判断下述说法中正确的是(??? )
A. 把入射平行光由绿光换成紫光后,屏上干涉条纹中相邻两条明纹间的距离就变大
B. 把入射光由绿光换成红光后,屏上干涉条纹中相邻两条明纹间的距离就变大
C. 入射光为单色平行光,当双缝S1、S2之间的距离变小时,屏上干涉条纹中相邻两条明纹间的距离变小
D. 若入射光为白光,将缝S1左边加红色滤光片(只透过红光),将缝S2左边加蓝色滤光片(只透过蓝光),则屏上出现彩色干涉条纹
1801年,托马斯·杨(图甲)用双缝干涉实验研究了光波的性质,证实了光的波动性,在光的波动说中具有重要的地位和意义。如图乙所示为双缝干涉实验装置,单缝S在双缝S1、S2的中心对称轴上,实验中在屏上P点刚好得到的是中央亮纹上方第3级亮纹,现要使P处出现中央亮纹上方第4级亮纹,可采取的措施有(????)
A. 适当增大屏到双缝的距离 B. 适当增大单缝到双缝的距离
C. 换用频率更低的单色光 D. 换用波长更短的单色光
二、多选题
在双缝干涉实验中,用蓝色激光照射在双缝上,在缝后的屏幕上显示出干涉图样。若要增大干涉图样中两相邻亮条纹的间距,可选用的方法是
A. 增大双缝间距 B. 改用红色激光
C. 增大屏幕与双缝的间距 D. 增大光源与双缝的间距
如图所示,在利用双缝干涉测量光的波长的实验中,单缝S0、双缝中点O、屏上的P0点均位于双缝S1和S2的中垂线上,屏上P点处是P0上方的第3条亮条纹(不包括P0点处的亮条纹)的中心。已知入射光在真空中的波长为λ,真空中的光速为c,双缝S1与S2之间距离为d,双缝到屏的距离为L,若整个装置处于真空中,则下列说法正确的是(????)
A. 来自双缝S1和S2的光传播到P点处的时间差为3λc
B. 屏上P点和P0点之间仅能观察到两条暗条纹
C. 仅将单缝S0向左(保持S0在双缝的中垂线上)移动的过程中,P点处能观察到暗条纹
D. 仅将屏向右(保持P0在双缝的中垂线上)移动的过程中,P点处能观察到暗条纹
如图甲所示,在平静的水面下深h处有一个点光源s,它发出的两种不同颜色的a光和b光在水面上形成了一个有光线射出的圆形区域,该区域的中间为由ab两种单色光所构成的复色光圆形区域周围为环状区域,且为a光的颜色(见图乙)设b光的折射率为nb,则下列说法正确的是(????)
A. 在水中,a光的波长比b光小
B. 在水中,a光的传播速度比b光大
C. 复色光圆形区域的面积为S=π?2nb2?1
D. 在同一装置的杨氏双缝干涉实验中,a光的干涉条纹比b光窄
下列说法中正确的是(????)
A. 变化的电场一定产生变化的磁场
B. 电磁波是横波
C. 紫外线的频率比红外线的频率大
D. 障碍物的尺寸比光的波长大时,不能发生光的衍射现象
E. 在“双缝干涉实验”中,其它条件不变,若双缝间距越大,屏上相邻亮条纹间距越小
三、实验题
在“用双缝干涉测量光的波长”的实验中,将双缝干涉实验仪按要求安装在光具座上,如图甲所示,并选用缝间距d=0.2mm的双缝屏。从仪器注明的规格可知,像屏与双缝屏间的距离L=700mm。接通电源使光源正常工作。
(1)M、N、P三个光学元件依次为________。
A.滤光片、单缝片、双缝片????????????????????????? B.滤光片、双缝片、单缝片
C.偏振片、单缝片、双缝片????????????????????????? D.双缝片、偏振片、单缝片
(2)对于某种单色光,为增加相邻亮条纹(暗条纹)间的距离,可采取的方法有________。
A.减小双缝间距离??????????????????????????????????????? B.增大单缝的宽度
C.减小透镜与光源的距离???????????????????????????? D.增大双缝到屏的距离
(3)已知测量头主尺的最小刻度是毫米,副尺上有50分度。某同学调整手轮后,从测量头的目镜看去,第1次映入眼帘的干涉条纹如图乙所示,图中的数字是该同学给各暗条纹的编号,此时游标卡尺如图丙所示,读数为x1=1.16mm;接着再转动手轮,映入眼帘的干涉条纹如图丁所示,此时游标卡尺如图戊所示,读数为x2=________mm。
(4)利用上述测量结果,经计算可得两个相邻亮条纹(或暗条纹)的距离Δx,进而计算得到这种色光的彼长λ=________nm。
(5)一同学通过测量头的目镜观察单色光的干涉图样时,发现里面的亮条纹与分划板竖线未对齐,如图己所示。若要使两者对齐,该同学应________。
A.仅左右转动透镜??????????????????????????????????????? B.仅旋转滤光片
C.仅拨动拨杆?????????????????????????????????????????????? D.仅旋转测量头
某实验小组利用如图甲所示的双缝干涉装置测量光的波长。
(1).按照实验装置,转动测量头的手轮,使分划板的中心刻线对准第1条亮条纹,手轮的示数如图乙所示。继续转动手轮,使分划板的中心刻线对准第11条亮条纹,手轮的示数如图丙所示,则相邻两亮条纹间的距离是_______mm。
(2).已知单缝与双缝的距离L1=60mm,双缝与光屏的距离L2=700mm,单缝宽d1=0.10mm,双缝间距d2=0.25mm。则待测光的波长是_____nm(保留三位有效数字)。
利用所学物理知识解答问题:
(1)如图甲所示是用双缝干涉测光波波长的实验设备示意图,图中①是光源,②是滤光片,③是单缝,④是双缝,⑤是光屏。下列操作能增大光屏上相邻两条亮纹之间距离的是______
A.增大③和④之间的距离
B.增大④和⑤之间的距离
C.将绿色滤光片改成红色滤光片
D.增大双缝之间的距离
(2)如果将灯泡换成激光光源,该实验照样可以完成,这时可以去掉的部件是______(填数字代号)。
(3)转动测量头的手轮,使分划板中心刻线对准第1条亮纹,读出手轮的读数如图乙所示。继续转动手轮,使分划板中心刻线对准第10条亮纹,读出手轮的读数如图丙所示。则相邻两亮条纹的间距是______mm。
(4)如果已经量得双缝的间距是0.30mm、双缝和光屏之间的距离是900mm,则待测光的波长是______m.(取三位有效数字)
利用双缝干涉测定光的波长的实验中,双缝间距d=0.4mm,双缝到光屏间的距离l=0.5m,用某种单色光照射双缝得到干涉条纹如图所示,分划板在图中A、B位置时游标卡尺读数也如图中所给出,则:
(1)分划板在图中A、B位置时游标卡尺读数分别为xA=______mm,xB=______mm,相邻两条亮条纹中心之间的距离为△x=______mm。
(2)该单色光的波长λ=______m。
(3)若增大双缝的间距,其他条件保持不变,则得到的干涉条纹间距将______(填“变大”“不变”或“变小”);若改用频率较高的单色光照射,其他条件保持不变,则得到的干涉条纹间距将______(填“变大”“不变”或“变小”)。
在“用双缝干涉测量光的波长”的实验中,将双缝干涉实验仪按要求安装在光具座上(如图所示),并选用缝间距d=0.2?mm的双缝屏.从仪器注明的规格可知,像屏与双缝屏间的距离L=700?mm.然后,接通电源使光源正常工作.
(1)已知测量头主尺的最小刻度是毫米,副尺上有50分度.某同学调整手轮后,从测量头的目镜看去,第1次映入眼帘的干涉条纹如图甲所示,图中的数字是该同学给各暗条纹的编号,此时图乙中游标卡尺上的读数x1=1.16?mm;接着再转动手轮,映入眼帘的干涉条纹如图丙所示,此时图丁中游标卡尺上的读数x2=____________?mm;
(2)利用上述测量结果,经计算可得两个相邻亮条纹(或暗条纹)间的距离Δx=________?mm;这种色光的波长λ=________?nm.
答案和解析
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】B
7.【答案】D
8.【答案】B
9.【答案】D
【解答】
由于想将原来的第3级亮纹变成第四级亮纹,说明两相邻亮条纹的距离变短了,根据公式Δx=Ldλ,L为屏到双缝的距离,d为双缝之间的距离,λ为波长,可知换用波长更短的单色光可以实现目的。
故答案为D。
10.【答案】BC
【解答】
根据双缝干涉条纹间距公式Δx=Ldλ知,增大入射光的波长,减小双缝间距,以及增大屏与双缝的距离,可以增大条纹的间距,由于红光的波长大于蓝光的波长,可知改用红色激光可以增大条纹间距,故BC正确。
11.【答案】AD
【解析】解:A、根据题意可知,P点到双缝的光程差为△x=3λ,
所以来自双缝S1和S2的光传播到P点处的时间差为△t=3λc,故A正确;
B、由题意可知,屏上P点和P0点之间仅能观察到三条暗条纹,故B错误;
C、仅将单缝S0向左移动的过程中,光源到P点的光程差不变,仍然为3λ,所以P点还是亮条纹,故C错误;
D、仅将屏向右移动的过程中,P点到光源的光程差逐渐发生变化,当P到光源的光程差为半个波长的奇数倍时,P点观察到暗条纹,故D正确。
12.【答案】BC
【解答】
AB.a光在水面上形成的圆形亮斑面积较大,知a光的临界角较大,根据sinC=1n,知a光的折射率较小,再由v=cn=λf,可知,在水中,a光的波长比b光大,a光的传播速度比b光大,故A错误,B正确;
C.依据sinC=1n,结合几何关系,可知,r?2+r2=1nb,而复色光圆形区域的面积为S=πr2=π?2nb2?1,故C正确;
D.a光的折射率小,波长长,根据双缝干涉条纹与波长成正比,可知相同条件下,a光干涉条纹比b光宽,故E错误。
13.【答案】BCE
【解析】解:A、根据麦克斯韦电磁场理论,可知变化的电场产生磁场,均匀变化的电场产生稳定的磁场,故A错误;
B、光的偏振现象说明电磁波是横波,故B正确;
C、根据电磁波谱可知紫外线的频率比红外线的频率大,故C正确;
D、障碍物的尺寸比光的波长大时,能发生光的衍射现象,只不过衍射现象不会很明显,故D错误;
E、在“双缝干涉实验”中,据△x=Ldλ,可知其它条件不变,若双缝间距越大,屏上相邻亮条纹间距越小,故E正确。
14.【答案】(1)A;
(2)AD;
(3)15.02?;
(4)660;
(5)D。
【解答】(1)双缝干涉实验是让单色光通过双缝在光屏上形成干涉图样,所以让白炽灯光通过滤光片形成单色光,再经过单缝形成线光源,再通过双缝形成干涉条纹。故自光源起合理的顺序是滤光片、单缝片、双缝片,选A。
(2)根据相邻亮条纹间的距离为Δx=Ldλ,为增加相邻亮条纹(暗条纹)间的距离,可减小双缝间距离或增大双缝到屏的距离,AD正确,BC错误。
(3)题图戊中,游标卡尺的主尺读数为15mm,游标读数为0.02mm×1=0.02mm,所以最终读数为x2=15.02mm。
(4)两个相邻亮条纹(或暗条纹)间的距离,
根据,得。
(5)旋转测量头,分划板竖线随之旋转,可使分划板竖线与亮条纹对齐,故选D。
15.【答案】(1)1.449;(2)518
16.【答案】(1)BC;(2)②③;(3)1.61;(4)5.37×10?7
【解答】
(1)根据Δx=Ldλ知,为增大相邻亮纹(暗纹)间的距离,可采取增大双缝到光屏的距离、减小双缝间距离、或增大入射光的波长,而单缝与双缝间距不会影响条纹间距。故BC正确,AD错误。
故选BC。
(2)将灯泡换成激光光源,激光的单色性好,不需要滤光片与单缝,即为②与③。
(3)图乙中固定刻度读数为0.0mm,可动刻度读数为0.01mm×4.5=0.045mm,所以最终读数x1=0.045mm。
图丙中固定刻度读数为14.5mm,可动刻度读数为:0.01mm×3.5=0.035mm,所以最终读数x10=14.535mm。
根据Δx=14.535?0.04510?1mm=1.61mm;
(4)相邻干涉条纹的间距Δx=1.61mm=1.61×10?3m;
由Δx=Ldλ得λ=Δx?dL=1.61×10?3×0.3×10?30.9m=5.37×10?7m。
17.【答案】(1)11.1,15.6,0.75;(2)6×10?7;(3)变小,变小。
【解析】解:(1)十等分的游标卡尺,其精确度为0.1mm,
A位置游标卡尺的读数为:11mm+0.1×1mm=11.1mm;
B位置游标卡尺的读数为:15mm+0.1×6mm=15.6mm;
相邻两条纹间距:△x=xB?xA6=0.75mm。
(2)根据△x=Ldλ知波长的表达式为:λ=△x?dl
解得波长为:λ=0.75×10?3×0.4×10?30.5m=6×10?7m。
(3)根据△x=Ldλ知,增大双缝的间距,其他条件保持不变,则得到的干涉条纹间距变小;频率变高,波长变小,则干涉条纹的间距变小。
18.【答案】(1)15.02;(2)2.31;660
【解答】
(1)图游标卡尺的主尺读数为15mm,游标读数为0.02×1=0.02mm,所以最终读数为15.02mm;
(2)两个相邻明纹(或暗纹)间的距离Δx=x2?x1n=15.02?1.166mm=2.31mm
根据Δx=Ldλ得,λ=ΔxdL=2.31×10?3×0.2×10?30.7m=6.60×10?7m=660nm.
故答案为:(1)15.02;(2)2.31;660。
