8.2 气体的等容变化和等压变化—2020-2021学年人教版高中物理选修3-3同步检测(word含答案)
文档属性
| 名称 | 8.2 气体的等容变化和等压变化—2020-2021学年人教版高中物理选修3-3同步检测(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 164.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-25 00:00:00 | ||
图片预览




文档简介
气体的等容变化和等压变化练习
一、单选题
在冬季,剩有半瓶热水的暖水瓶经过一个夜晚后,第二天拔瓶口的软木塞时觉得很紧,不易拔出来,产生这种现象的主要原因是(????)
A. 软木塞受潮膨胀 B. 瓶口因温度降低而收缩变小
C. 白天气温升高,大气压强变大 D. 瓶内气体因温度降低而压强减小
如图所示,一定质量的理想气体由状态A变化到状态B再变化到状态C,其中状态A到状态B过程为等压变化过程,状态B到状态C过程为等容变化过程,A、C两个状态处在同一条双曲线上,则下列说法正确的是(????)
A. 状态A到状态B过程,气体放出热量
B. 状态A到状态B过程,气体对外做功,内能增加
C. 状态B到状态C过程,气体内能增加
D. 状态A到状态B,再到状态C过程,气体分子的平均动能先减小后增大
如图,容器被绝热活塞分成两部分,分别装有理想气体A、B.开始时,A的温度为TA,B的温度为TB,且TA>TB.气体A、B均处于平衡状态,活塞静止.加热容器,使两边气体缓慢升高相同的温度,若不计活塞的摩擦,则活塞将(????)
A. 向右移动 B. 向左移动
C. 保持不动 D. 因体积未知而无法确定
两端封闭、内径均匀的直玻璃管竖直放置,如图.两端空气柱体积V上 A. 不动 B. 向上移动
C. 向下移动 D. 无法确定是否移动
如图所示,一导热性能良好的汽缸内用活塞封住一定质量的气体(不计活塞与缸壁的摩擦),大气压强不变,环境温度升高时,下列说法正确的是(????)
A. 缸内气体压强增大
B. 汽缸高度H增大
C. 活塞高度h减小
D. 单位时间内撞击单位面积器壁的分子数增多
一定质量的气体,体积保持不变,下列过程可以实现的是(????)
A. 温度不变,压强减小 B. 温度升高,压强减小
C. 温度不变,压强增大 D. 温度升高,压强增大
如图所示,一开口向右的气缸固定在水平地面上,活塞可无摩擦移动且不漏气,气缸中间位置有一挡板,外界大气压为p0。初始时,活塞紧压挡板处;现缓慢升高缸内气体温度,则图中能正确反应缸内气体压强变化情况的p?T图象是(??)
A. B.
C. D.
一定质量的理想气体在等压变化中体积增大了12,若气体原来温度为27?℃,则温度的变化是(????)
A. 升高了450?K B. 升高了150?℃ C. 升高了40.5?℃ D. 升高了450?℃
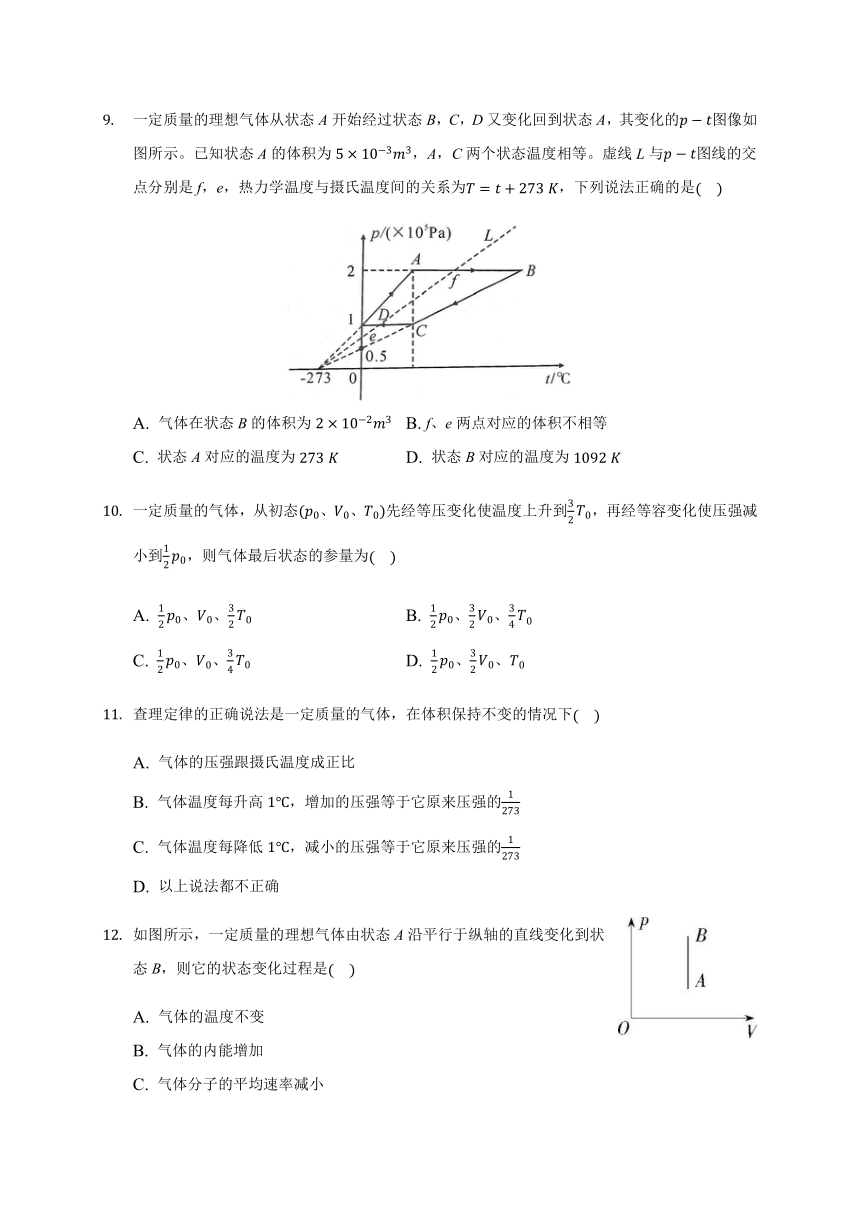
一定质量的理想气体从状态A开始经过状态B,C,D又变化回到状态A,其变化的p?t图像如图所示。已知状态A的体积为5×10?3m3,A,C两个状态温度相等。虚线L与p?t图线的交点分别是f,e,热力学温度与摄氏温度间的关系为T=t+273?K,下列说法正确的是(????)
A. 气体在状态B的体积为2×10?2m3 B. f、e两点对应的体积不相等
C. 状态A对应的温度为273?K D. 状态B对应的温度为1092?K
一定质量的气体,从初态(p0、V0、T0)先经等压变化使温度上升到32T0,再经等容变化使压强减小到12p0,则气体最后状态的参量为(????)
A. 12p0、V0、32T0 B. 12p0、32V0、34T0???????
C. 12p0、V0、34T0 D. 12p0、32V0、T0
查理定律的正确说法是一定质量的气体,在体积保持不变的情况下(????)
A. 气体的压强跟摄氏温度成正比
B. 气体温度每升高1℃,增加的压强等于它原来压强的1273
C. 气体温度每降低1℃,减小的压强等于它原来压强的1273
D. 以上说法都不正确
如图所示,一定质量的理想气体由状态A沿平行于纵轴的直线变化到状态B,则它的状态变化过程是(????)
A. 气体的温度不变
B. 气体的内能增加
C. 气体分子的平均速率减小
D. 气体分子在单位时间内与器壁单位面积上碰撞的次数不变
二、多选题
图示为一定质量的某种气体的等容或等压变化图象,下列关于这两个图象的说法正确是(????)。
A. 甲是等压线,乙是等容线
B. 乙图中р?t线与t轴交点对应的温度是?273.15℃,而甲图中V?t线与t轴的交点不一定是?273.15℃
C. 由乙图可知,一定质量的气体,在任何情况下都是р与t成直线关系
D. 乙图表明温度每升高1℃,压强增加相同,但甲图表明随温度的升高压强不变
用如图所示的实验装置来研究气体等体积变化的规律.A、B管下端由软管相连,注入一定量的水银,烧瓶中封有一定量的理想气体,开始时A、B两管中水银面一样高,那么为了保持瓶中气体体积不变(????)
A. 将烧瓶浸入热水中时,应将A管向上移动
B. 将烧瓶浸入热水中时,应将A管向下移动
C. 将烧瓶浸入冰水中时,应将A管向上移动
D. 将烧瓶浸入冰水中时,应将A管向下移动
如图所示,一根内径均匀,一端封闭,另一端开口的直玻璃管,长l=1m,用一段长?=14cm的水银柱封闭了长l0=60cm的气体。这时外部的大气压p0=76cmHg,气体温度t0=27℃,给气体缓慢加热,使液柱上升到管口时,气体温度为T1,继续加热至温度为T2后停止加热,液柱会自行全部离开玻璃管,则(????)
A. T1=430K B. T1=38.7℃ C. T2=430.22K D. T2无法确定
如图是一定质量的理想气体三种升温过程.那么,以下四种解释中正确的是(????)
A. a→d的过程气体的体积增大
B. b→d的过程气体的体积不变
C. c→d的过程气体的体积增大
D. a→d的过程气体的体积减小
三、计算题(本大题共3小题,共30.0分)
如图,一固定的竖直汽缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞.已知大活塞的质量为m1=2.50?kg,横截面积为S1=80.0?cm2;小活塞的质量为m2=1.50?kg,横截面积为S2=40.0?cm2;两活塞用刚性轻杆连接,间距为L=40.0?cm;汽缸外大气的压强为p0=1.00×105Pa,温度为T=303?K.初始时大活塞与大圆筒底部相距L2,两活塞间封闭气体的温度为T1=495?K.刚开始活塞处于平衡态。现让汽缸内气体温度缓慢下降,活塞缓慢下移.忽略两活塞与汽缸壁之间的摩擦,重力加速度大小g取10?m/s2.求:
(1)刚开始时,气缸中中的气体压强是多大?
(2)在大活塞与大圆筒底部接触前的瞬间,汽缸内封闭气体的温度;
(3)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强.
一定质量的理想气体体积V与热力学温度T的关系图象如图所示,气体在状态A时的压强pA=p0,温度TA=T0,线段AB与V轴平行,BC的延长线过原点。求:
(1)气体在状态B时的压强pB。
(2)气体在状态C时的压强pC和温度TC。
如图所示,内壁光滑、足够高的圆柱形汽缸竖直放置,内有一质量为m的活塞封闭一定质量的理想气体。已知活塞横截面积为S,外界大气压强为p0,缸内气体温度为T0。现对汽缸内气体缓慢加热,使气体体积由V1增大到V2,该过程中气体吸收的热量为Q1,停止加热并保持体积V2不变,使其降温到T0,已知重力加速度为g,求:
(1)停止加热时缸内气体的温度;
(2)降温过程中气体放出的热量。
答案和解析
1.【答案】D
【解答】
一开始暖瓶塞受力平衡如图:
??
由于暖水瓶内气体的体积不变,经过一晚的时间,瓶内的温度会降低,即气体的温度降低,?根据查理定律得:p1T1=p2T2?由于T1>T2,所以p1>p2,?即暖瓶内的压强由原来的p1减小为现在的p2,外界大气压力大于内部气体的压力,所以拔出瓶塞更费力,故D正确,ABC错误。
故选D。
2.【答案】B
【解答】
AB.从状态A→状态B的过程,气体发生等压变化,体积增大,根据盖?吕萨克定律得:VATA=VBTB,知温度升高,一定质量的理想气体内能由温度决定,因此气体内能增加,根据热力学第一定律ΔU=W+Q,由于体积增大,气体对外做功,所以气体吸收热量,故A错误,B正确;
C.从状态B→状态C的过程,气体发生等容变化,根据查理定律得:pBTB=pCTC,可知由于压强减小,温度降低,因此气体内能减小,故C错误;
D.温度是分子平均动能的标志,从状态A→状态B→状态C的过程,由于气体温度先升高后降低,因此气体分子的平均动能先增大后减小,故D错误。
故选B。
3.【答案】B
【解析】【试题解析】
解:假设活塞不移动,气体发生等容变化,根据查理定律有
pT=ΔpΔT
得Δp=pT?ΔT
根据题意知,升高相同的温度△T相同,原来平衡,pA?=pB?
TA?>TB?
得ΔpA<ΔpB
△F=△p?S
所以ΔFB>ΔFA,所以活塞将向左移动,故B正确,ACD错误;
故选:B
采用假设法,气体发生等容变化,根据查理定律定性分析两侧气体压强的变化量,再由△F=△p?S分析压力的变化量;
4.【答案】C
【解答】
假设水银柱不动,则气体体积不变,
由查理定律得:pT=p′T′,则△p=p′?p=ΔTTp,
开始时两部分气体压强p上上边气体降低的压强:△p上=20?10Tp上=10Tp上
下边气体降低的压强:△p下=20?10Tp下=10Tp下,
上边气体降低的压强小于下边气体降低的压强,
则水银柱将向下移动;
故选:C.
5.【答案】B
【解答】
A.设气缸的质量为m,横截面积为S,封闭气体的压强:p=p0+?mg?S,大气压不变、m、S不变,气体温度升高时,封闭气体的压强保持不变,故A错误;
B.气体压强p不变而温度T升高,由盖吕萨克定律可知,气体体积V增大,气缸上升,H增大,故B正确;
C.气缸与活塞质量不变,弹簧长度不变,h不变,故C错误;
D.根据压强的微观解释可知,因为压强不变,温度升高,体积增大,单位时间内撞击单位面积器壁的分子数减少,故D错误。
故选B。
6.【答案】D
【解答】
一定质量的气体,体积保持不变,根据查理定律pT=c可知,温度升高,压强增大;温度不变,压强也不变,故D正确,ABC错误。
故选D。
7.【答案】A
【解答】
当缓慢升高缸内气体温度时,气体先发生等容变化,根据查理定律,缸内气体的压强P与热力学温度T成正比,图线是过原点的倾斜的直线;当缸内气体的压强等于外界的大气压时,气体发生等压膨胀,图线是平行于T轴的直线。
故选A。
8.【答案】B
【解答】
根据盖—吕萨克定律,可得ΔVΔT=V1T1,ΔT=T1V1ΔV=(273+27)?KV×12V=150?K.升高了150?K和升高了150?℃是等效的,故B正确.
故选B。
9.【答案】D
【解答】
p?t图线中过?273℃的倾斜直线表示气体做等容变化
A.由于BC线为等容线,即气体从状态B到状态C体积不变,而气体从A到C做等温变化,根据玻意耳定律有pAVA=pCVC,解得VB=VC=2VA=1×10?2m3,故A错误;
B.f、e两点在一条等容线上,故f、e两点对应的体积相等,故B错误;
C.气体从D到A过程做等容变化,则pATA=pDTD,解得TA=2TD=546K=273℃,故C错误;
D.气体从B到C过程为等容变化,根据查理定律有pBTB=pCTC,解得TB=2TC=2TA=1092K,故D正确。
故选D。
10.【答案】B
【解答】
等压过程初状态:V1=V0,T1=T0,末状态:T2=32T0,
根据盖·吕萨克定律有:V1T1=V2T2,解得V2=32V0,
此后的等容过程初状态:p2=p0,T2=32T0,末状态:p3=12p0,
根据查理定律有:p2T2=p3T3,解得T3=34T0,
所以气体最后状态的参量:12p0、32V0、34T0?,故B正确,ACD错误。
11.【答案】D
【解答】
A.一定质量的气体,在体积保持不变的情况下,气体的压强跟热力学温度成正比。故A错误;
BC.任何理想气体都是温度每升高1℃增加的压强△P等于它在0℃时压强P0的1273.故BC错误;
D.以上说法都不正确。故D正确;
故选:D。
12.【答案】B
13.【答案】AD
【解答】
A.由查理定律p=CT=C(t+273.15K)及盖—吕萨克定律V=CT=C(t+273.15K)可知,甲图是等压线,乙图是等容线,故A正确;
B.由“外推法”可知两种图线的反向延长线与t轴的交点温度为?273.15℃,即热力学温度的0K,故B错误;
C.查理定律及盖—吕萨克定律是气体的实验定律,都是在温度不太低、压强不太大的条件下得出的,当压强很大、温度很低时,这些定律就不成立了,故C错误;
D.由上述分析,故D正确。
故选AD。
14.【答案】AD
【解析】解:AB、将烧瓶浸入热水中时,气体的温度升高,由于气体的体积不变,所以气体的压强要变大,应将A管向上移动,所以A正确,B错误;
CD、将烧瓶浸入冰水中时,气体的温度降低,由于气体的体积不变,所以气体的压强要减小,应将A管向下移动,所以C错误,D正确;
故选:AD。
气体做的是等容变化,根据气体的温度的变化,由查理定律分析压强的变化即可.
气体做的是等容变化,直接根据查理定律分析即可,比较简单.
15.【答案】AC
【解答】
AB.液柱上升到管口过程中,气体做等圧变化,根据盖?吕萨克定律,可知:l0ST0=l??ST1,将T0=t0+273=300K代入可得T1=430K=157°C,故A正确,B错误;
CD.当液柱上升到管口后,水银开始排出,由于PVT=C,当管内水银开始排出后,空气体积增大,而压强减小,当PV值增大,则温度继续升高,当PV值达到最大后,液柱便会自行全部离开玻璃管,设此时由于水银溢出而使得水银缩短了x,则从开始加热到该过程有:p0+?l0ST0=p0+xl?xST2,解得T2=?x2+24x+760018,故当x=12cm时,T2最大,此时T2=430.22K,故C正确,D错误。
故选AC。
16.【答案】AB
【解答】
如图:
,
连接aO、cO,则aO、cO、dO均可表示气体发生等容变化,由气态方程pVT=C知:
AD.由状态a变到状态d的过程中,pT减小,则气体的体积增大,故A正确,D错误;
B.由状态b变到状态d的过程中,气体发生等容变化,故体积不变,故B正确;
C.由状态c变到状态d的过程中,倾角变大,则pT变大,故气体体积减小,故C错误。
故选AB。
17.【答案】解:
(1)由于刚开始活塞处于平衡状态,对大活塞、杆和小活塞整体进行受力分析,由平衡条件可得:p0S1+m1+m2g+p1S2=p0S2+p1S1
代入数据解得此时汽缸中的气体压强是p1=1.1×105Pa
(2)大活塞与大圆筒底部接触前气体发生等压变化,
气体的状态参量:V1=(L?L2)S2+L2S1=(40?402)×40+402×80=2400cm3
T1=495K,V2=S2L=40×40=1600cm3,
由盖吕萨克定律得:V1T1=V2T2,即:2400495=1600T2,解得:T2=330K;
(2)大活塞与大圆筒底部接触后到气缸内气体与气缸外气体温度相等过程中气体发生等容变化,
大活塞刚刚与大圆筒底部接触时,由平衡条件得:p0S1+p2S2+(m1+m2)g=p2S1+p0S2,
代入数据解得:p2=1.1×105Pa,T2=330K,T3=T=303K,
由查理定律得:p2T2=p3T3,
解得:p3=1.01×105Pa;
18.【答案】解:(1)A到B是等温变化,压强和体积成反比,
根据玻意耳定律有:pAVA=pBVB,解得:pB=p02
(2)由B到C是等压变化,根据盖?吕萨克定律得:VBTB=VCTC,
解得:TC=12T0
A到C是等容变化,根据查理定律得:pATA=pCTC
解得:pC=p02
答:(1)气体在状态B时的压强pB为p02;
(2)气体在状态C时的压强pC为p02,温度TC为T02。
【解析】(1)由图象可知A到B等温变化,根据玻意而定律列式求解;
(2)由B到C等压变化,根据盖吕萨克定律可求C点的温度,A到C等容变化,根据查理定律可求C点压强。
本题考查了玻意耳定律、盖?吕萨克定律,关键是读懂图象,能从图象中判断各个过程气体做何种变化,选择合适气体实验定律列式求解。
19.【答案】解:
(1)加热过程中气体等压膨胀,由盖—吕萨克定律V1T0=V2T,得:T=V2V1T0。
(2)设加热过程中,封闭气体内能增加ΔU,因气体体积增大,故此过程中气体对外做功,W<0。
由热力学第一定律知:ΔU=Q1+W
其中W=?pΔV=?p0+mgS(V2?V1)
由于理想气体内能只与温度有关,故再次降到原温度时气体放出的热量满足Q2=ΔU
整理可得:Q2=Q1?p0+mgS(V2?V1)。
一、单选题
在冬季,剩有半瓶热水的暖水瓶经过一个夜晚后,第二天拔瓶口的软木塞时觉得很紧,不易拔出来,产生这种现象的主要原因是(????)
A. 软木塞受潮膨胀 B. 瓶口因温度降低而收缩变小
C. 白天气温升高,大气压强变大 D. 瓶内气体因温度降低而压强减小
如图所示,一定质量的理想气体由状态A变化到状态B再变化到状态C,其中状态A到状态B过程为等压变化过程,状态B到状态C过程为等容变化过程,A、C两个状态处在同一条双曲线上,则下列说法正确的是(????)
A. 状态A到状态B过程,气体放出热量
B. 状态A到状态B过程,气体对外做功,内能增加
C. 状态B到状态C过程,气体内能增加
D. 状态A到状态B,再到状态C过程,气体分子的平均动能先减小后增大
如图,容器被绝热活塞分成两部分,分别装有理想气体A、B.开始时,A的温度为TA,B的温度为TB,且TA>TB.气体A、B均处于平衡状态,活塞静止.加热容器,使两边气体缓慢升高相同的温度,若不计活塞的摩擦,则活塞将(????)
A. 向右移动 B. 向左移动
C. 保持不动 D. 因体积未知而无法确定
两端封闭、内径均匀的直玻璃管竖直放置,如图.两端空气柱体积V上
C. 向下移动 D. 无法确定是否移动
如图所示,一导热性能良好的汽缸内用活塞封住一定质量的气体(不计活塞与缸壁的摩擦),大气压强不变,环境温度升高时,下列说法正确的是(????)
A. 缸内气体压强增大
B. 汽缸高度H增大
C. 活塞高度h减小
D. 单位时间内撞击单位面积器壁的分子数增多
一定质量的气体,体积保持不变,下列过程可以实现的是(????)
A. 温度不变,压强减小 B. 温度升高,压强减小
C. 温度不变,压强增大 D. 温度升高,压强增大
如图所示,一开口向右的气缸固定在水平地面上,活塞可无摩擦移动且不漏气,气缸中间位置有一挡板,外界大气压为p0。初始时,活塞紧压挡板处;现缓慢升高缸内气体温度,则图中能正确反应缸内气体压强变化情况的p?T图象是(??)
A. B.
C. D.
一定质量的理想气体在等压变化中体积增大了12,若气体原来温度为27?℃,则温度的变化是(????)
A. 升高了450?K B. 升高了150?℃ C. 升高了40.5?℃ D. 升高了450?℃
一定质量的理想气体从状态A开始经过状态B,C,D又变化回到状态A,其变化的p?t图像如图所示。已知状态A的体积为5×10?3m3,A,C两个状态温度相等。虚线L与p?t图线的交点分别是f,e,热力学温度与摄氏温度间的关系为T=t+273?K,下列说法正确的是(????)
A. 气体在状态B的体积为2×10?2m3 B. f、e两点对应的体积不相等
C. 状态A对应的温度为273?K D. 状态B对应的温度为1092?K
一定质量的气体,从初态(p0、V0、T0)先经等压变化使温度上升到32T0,再经等容变化使压强减小到12p0,则气体最后状态的参量为(????)
A. 12p0、V0、32T0 B. 12p0、32V0、34T0???????
C. 12p0、V0、34T0 D. 12p0、32V0、T0
查理定律的正确说法是一定质量的气体,在体积保持不变的情况下(????)
A. 气体的压强跟摄氏温度成正比
B. 气体温度每升高1℃,增加的压强等于它原来压强的1273
C. 气体温度每降低1℃,减小的压强等于它原来压强的1273
D. 以上说法都不正确
如图所示,一定质量的理想气体由状态A沿平行于纵轴的直线变化到状态B,则它的状态变化过程是(????)
A. 气体的温度不变
B. 气体的内能增加
C. 气体分子的平均速率减小
D. 气体分子在单位时间内与器壁单位面积上碰撞的次数不变
二、多选题
图示为一定质量的某种气体的等容或等压变化图象,下列关于这两个图象的说法正确是(????)。
A. 甲是等压线,乙是等容线
B. 乙图中р?t线与t轴交点对应的温度是?273.15℃,而甲图中V?t线与t轴的交点不一定是?273.15℃
C. 由乙图可知,一定质量的气体,在任何情况下都是р与t成直线关系
D. 乙图表明温度每升高1℃,压强增加相同,但甲图表明随温度的升高压强不变
用如图所示的实验装置来研究气体等体积变化的规律.A、B管下端由软管相连,注入一定量的水银,烧瓶中封有一定量的理想气体,开始时A、B两管中水银面一样高,那么为了保持瓶中气体体积不变(????)
A. 将烧瓶浸入热水中时,应将A管向上移动
B. 将烧瓶浸入热水中时,应将A管向下移动
C. 将烧瓶浸入冰水中时,应将A管向上移动
D. 将烧瓶浸入冰水中时,应将A管向下移动
如图所示,一根内径均匀,一端封闭,另一端开口的直玻璃管,长l=1m,用一段长?=14cm的水银柱封闭了长l0=60cm的气体。这时外部的大气压p0=76cmHg,气体温度t0=27℃,给气体缓慢加热,使液柱上升到管口时,气体温度为T1,继续加热至温度为T2后停止加热,液柱会自行全部离开玻璃管,则(????)
A. T1=430K B. T1=38.7℃ C. T2=430.22K D. T2无法确定
如图是一定质量的理想气体三种升温过程.那么,以下四种解释中正确的是(????)
A. a→d的过程气体的体积增大
B. b→d的过程气体的体积不变
C. c→d的过程气体的体积增大
D. a→d的过程气体的体积减小
三、计算题(本大题共3小题,共30.0分)
如图,一固定的竖直汽缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞.已知大活塞的质量为m1=2.50?kg,横截面积为S1=80.0?cm2;小活塞的质量为m2=1.50?kg,横截面积为S2=40.0?cm2;两活塞用刚性轻杆连接,间距为L=40.0?cm;汽缸外大气的压强为p0=1.00×105Pa,温度为T=303?K.初始时大活塞与大圆筒底部相距L2,两活塞间封闭气体的温度为T1=495?K.刚开始活塞处于平衡态。现让汽缸内气体温度缓慢下降,活塞缓慢下移.忽略两活塞与汽缸壁之间的摩擦,重力加速度大小g取10?m/s2.求:
(1)刚开始时,气缸中中的气体压强是多大?
(2)在大活塞与大圆筒底部接触前的瞬间,汽缸内封闭气体的温度;
(3)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强.
一定质量的理想气体体积V与热力学温度T的关系图象如图所示,气体在状态A时的压强pA=p0,温度TA=T0,线段AB与V轴平行,BC的延长线过原点。求:
(1)气体在状态B时的压强pB。
(2)气体在状态C时的压强pC和温度TC。
如图所示,内壁光滑、足够高的圆柱形汽缸竖直放置,内有一质量为m的活塞封闭一定质量的理想气体。已知活塞横截面积为S,外界大气压强为p0,缸内气体温度为T0。现对汽缸内气体缓慢加热,使气体体积由V1增大到V2,该过程中气体吸收的热量为Q1,停止加热并保持体积V2不变,使其降温到T0,已知重力加速度为g,求:
(1)停止加热时缸内气体的温度;
(2)降温过程中气体放出的热量。
答案和解析
1.【答案】D
【解答】
一开始暖瓶塞受力平衡如图:
??
由于暖水瓶内气体的体积不变,经过一晚的时间,瓶内的温度会降低,即气体的温度降低,?根据查理定律得:p1T1=p2T2?由于T1>T2,所以p1>p2,?即暖瓶内的压强由原来的p1减小为现在的p2,外界大气压力大于内部气体的压力,所以拔出瓶塞更费力,故D正确,ABC错误。
故选D。
2.【答案】B
【解答】
AB.从状态A→状态B的过程,气体发生等压变化,体积增大,根据盖?吕萨克定律得:VATA=VBTB,知温度升高,一定质量的理想气体内能由温度决定,因此气体内能增加,根据热力学第一定律ΔU=W+Q,由于体积增大,气体对外做功,所以气体吸收热量,故A错误,B正确;
C.从状态B→状态C的过程,气体发生等容变化,根据查理定律得:pBTB=pCTC,可知由于压强减小,温度降低,因此气体内能减小,故C错误;
D.温度是分子平均动能的标志,从状态A→状态B→状态C的过程,由于气体温度先升高后降低,因此气体分子的平均动能先增大后减小,故D错误。
故选B。
3.【答案】B
【解析】【试题解析】
解:假设活塞不移动,气体发生等容变化,根据查理定律有
pT=ΔpΔT
得Δp=pT?ΔT
根据题意知,升高相同的温度△T相同,原来平衡,pA?=pB?
TA?>TB?
得ΔpA<ΔpB
△F=△p?S
所以ΔFB>ΔFA,所以活塞将向左移动,故B正确,ACD错误;
故选:B
采用假设法,气体发生等容变化,根据查理定律定性分析两侧气体压强的变化量,再由△F=△p?S分析压力的变化量;
4.【答案】C
【解答】
假设水银柱不动,则气体体积不变,
由查理定律得:pT=p′T′,则△p=p′?p=ΔTTp,
开始时两部分气体压强p上
下边气体降低的压强:△p下=20?10Tp下=10Tp下,
上边气体降低的压强小于下边气体降低的压强,
则水银柱将向下移动;
故选:C.
5.【答案】B
【解答】
A.设气缸的质量为m,横截面积为S,封闭气体的压强:p=p0+?mg?S,大气压不变、m、S不变,气体温度升高时,封闭气体的压强保持不变,故A错误;
B.气体压强p不变而温度T升高,由盖吕萨克定律可知,气体体积V增大,气缸上升,H增大,故B正确;
C.气缸与活塞质量不变,弹簧长度不变,h不变,故C错误;
D.根据压强的微观解释可知,因为压强不变,温度升高,体积增大,单位时间内撞击单位面积器壁的分子数减少,故D错误。
故选B。
6.【答案】D
【解答】
一定质量的气体,体积保持不变,根据查理定律pT=c可知,温度升高,压强增大;温度不变,压强也不变,故D正确,ABC错误。
故选D。
7.【答案】A
【解答】
当缓慢升高缸内气体温度时,气体先发生等容变化,根据查理定律,缸内气体的压强P与热力学温度T成正比,图线是过原点的倾斜的直线;当缸内气体的压强等于外界的大气压时,气体发生等压膨胀,图线是平行于T轴的直线。
故选A。
8.【答案】B
【解答】
根据盖—吕萨克定律,可得ΔVΔT=V1T1,ΔT=T1V1ΔV=(273+27)?KV×12V=150?K.升高了150?K和升高了150?℃是等效的,故B正确.
故选B。
9.【答案】D
【解答】
p?t图线中过?273℃的倾斜直线表示气体做等容变化
A.由于BC线为等容线,即气体从状态B到状态C体积不变,而气体从A到C做等温变化,根据玻意耳定律有pAVA=pCVC,解得VB=VC=2VA=1×10?2m3,故A错误;
B.f、e两点在一条等容线上,故f、e两点对应的体积相等,故B错误;
C.气体从D到A过程做等容变化,则pATA=pDTD,解得TA=2TD=546K=273℃,故C错误;
D.气体从B到C过程为等容变化,根据查理定律有pBTB=pCTC,解得TB=2TC=2TA=1092K,故D正确。
故选D。
10.【答案】B
【解答】
等压过程初状态:V1=V0,T1=T0,末状态:T2=32T0,
根据盖·吕萨克定律有:V1T1=V2T2,解得V2=32V0,
此后的等容过程初状态:p2=p0,T2=32T0,末状态:p3=12p0,
根据查理定律有:p2T2=p3T3,解得T3=34T0,
所以气体最后状态的参量:12p0、32V0、34T0?,故B正确,ACD错误。
11.【答案】D
【解答】
A.一定质量的气体,在体积保持不变的情况下,气体的压强跟热力学温度成正比。故A错误;
BC.任何理想气体都是温度每升高1℃增加的压强△P等于它在0℃时压强P0的1273.故BC错误;
D.以上说法都不正确。故D正确;
故选:D。
12.【答案】B
13.【答案】AD
【解答】
A.由查理定律p=CT=C(t+273.15K)及盖—吕萨克定律V=CT=C(t+273.15K)可知,甲图是等压线,乙图是等容线,故A正确;
B.由“外推法”可知两种图线的反向延长线与t轴的交点温度为?273.15℃,即热力学温度的0K,故B错误;
C.查理定律及盖—吕萨克定律是气体的实验定律,都是在温度不太低、压强不太大的条件下得出的,当压强很大、温度很低时,这些定律就不成立了,故C错误;
D.由上述分析,故D正确。
故选AD。
14.【答案】AD
【解析】解:AB、将烧瓶浸入热水中时,气体的温度升高,由于气体的体积不变,所以气体的压强要变大,应将A管向上移动,所以A正确,B错误;
CD、将烧瓶浸入冰水中时,气体的温度降低,由于气体的体积不变,所以气体的压强要减小,应将A管向下移动,所以C错误,D正确;
故选:AD。
气体做的是等容变化,根据气体的温度的变化,由查理定律分析压强的变化即可.
气体做的是等容变化,直接根据查理定律分析即可,比较简单.
15.【答案】AC
【解答】
AB.液柱上升到管口过程中,气体做等圧变化,根据盖?吕萨克定律,可知:l0ST0=l??ST1,将T0=t0+273=300K代入可得T1=430K=157°C,故A正确,B错误;
CD.当液柱上升到管口后,水银开始排出,由于PVT=C,当管内水银开始排出后,空气体积增大,而压强减小,当PV值增大,则温度继续升高,当PV值达到最大后,液柱便会自行全部离开玻璃管,设此时由于水银溢出而使得水银缩短了x,则从开始加热到该过程有:p0+?l0ST0=p0+xl?xST2,解得T2=?x2+24x+760018,故当x=12cm时,T2最大,此时T2=430.22K,故C正确,D错误。
故选AC。
16.【答案】AB
【解答】
如图:
,
连接aO、cO,则aO、cO、dO均可表示气体发生等容变化,由气态方程pVT=C知:
AD.由状态a变到状态d的过程中,pT减小,则气体的体积增大,故A正确,D错误;
B.由状态b变到状态d的过程中,气体发生等容变化,故体积不变,故B正确;
C.由状态c变到状态d的过程中,倾角变大,则pT变大,故气体体积减小,故C错误。
故选AB。
17.【答案】解:
(1)由于刚开始活塞处于平衡状态,对大活塞、杆和小活塞整体进行受力分析,由平衡条件可得:p0S1+m1+m2g+p1S2=p0S2+p1S1
代入数据解得此时汽缸中的气体压强是p1=1.1×105Pa
(2)大活塞与大圆筒底部接触前气体发生等压变化,
气体的状态参量:V1=(L?L2)S2+L2S1=(40?402)×40+402×80=2400cm3
T1=495K,V2=S2L=40×40=1600cm3,
由盖吕萨克定律得:V1T1=V2T2,即:2400495=1600T2,解得:T2=330K;
(2)大活塞与大圆筒底部接触后到气缸内气体与气缸外气体温度相等过程中气体发生等容变化,
大活塞刚刚与大圆筒底部接触时,由平衡条件得:p0S1+p2S2+(m1+m2)g=p2S1+p0S2,
代入数据解得:p2=1.1×105Pa,T2=330K,T3=T=303K,
由查理定律得:p2T2=p3T3,
解得:p3=1.01×105Pa;
18.【答案】解:(1)A到B是等温变化,压强和体积成反比,
根据玻意耳定律有:pAVA=pBVB,解得:pB=p02
(2)由B到C是等压变化,根据盖?吕萨克定律得:VBTB=VCTC,
解得:TC=12T0
A到C是等容变化,根据查理定律得:pATA=pCTC
解得:pC=p02
答:(1)气体在状态B时的压强pB为p02;
(2)气体在状态C时的压强pC为p02,温度TC为T02。
【解析】(1)由图象可知A到B等温变化,根据玻意而定律列式求解;
(2)由B到C等压变化,根据盖吕萨克定律可求C点的温度,A到C等容变化,根据查理定律可求C点压强。
本题考查了玻意耳定律、盖?吕萨克定律,关键是读懂图象,能从图象中判断各个过程气体做何种变化,选择合适气体实验定律列式求解。
19.【答案】解:
(1)加热过程中气体等压膨胀,由盖—吕萨克定律V1T0=V2T,得:T=V2V1T0。
(2)设加热过程中,封闭气体内能增加ΔU,因气体体积增大,故此过程中气体对外做功,W<0。
由热力学第一定律知:ΔU=Q1+W
其中W=?pΔV=?p0+mgS(V2?V1)
由于理想气体内能只与温度有关,故再次降到原温度时气体放出的热量满足Q2=ΔU
整理可得:Q2=Q1?p0+mgS(V2?V1)。
