六年级数学下册试题 一课一练1.4《圆锥的体积》-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练1.4《圆锥的体积》-北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 279.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-25 16:07:19 | ||
图片预览



文档简介
1.4《圆锥的体积》
一、填空题
1.一个圆锥体积是,底面积是,高是 .
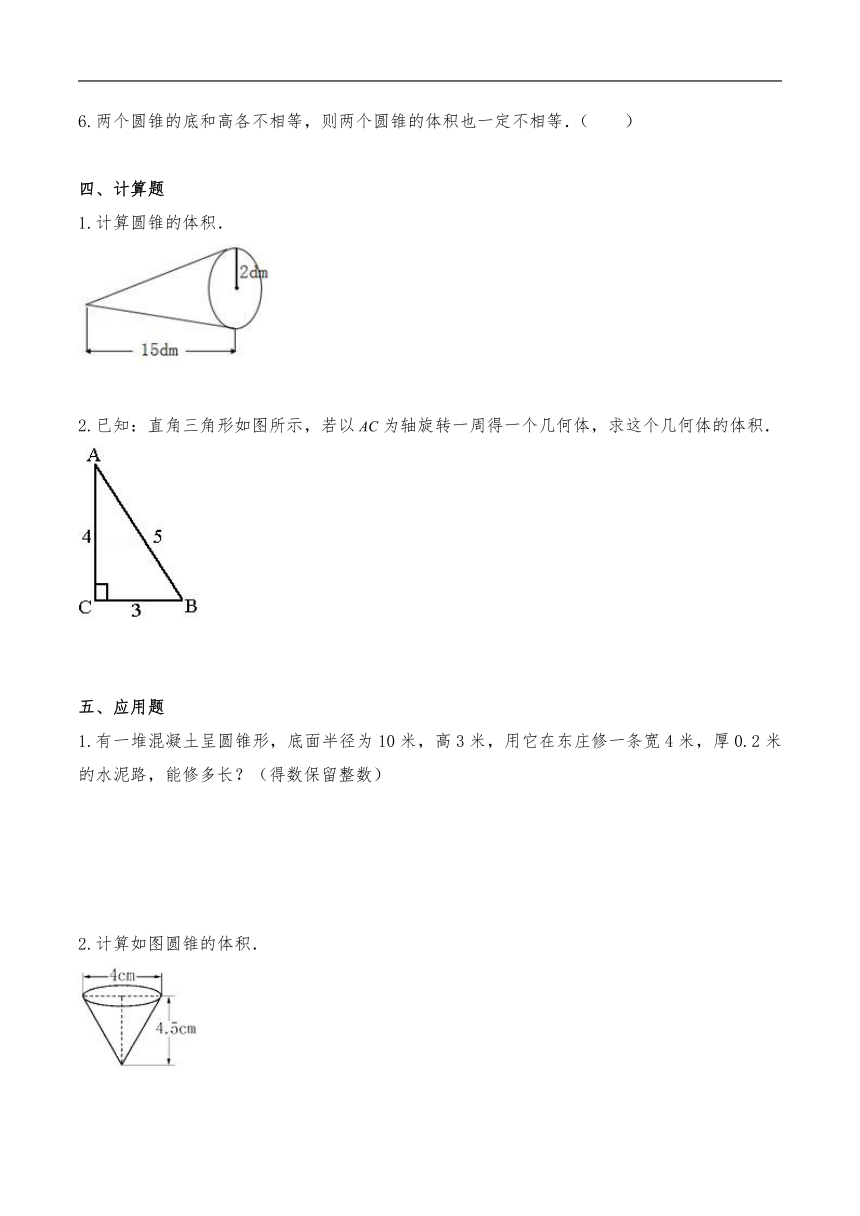
2.在下面两个空容器中,将甲容器注满水,再倒入乙容器,这时乙容器中的水深 .
3.一个直角三角形的三条边长分别是、和,若以直角边为轴旋转一圈,旋转一圈形成的图形体积是 立方厘米.取
4.一个圆柱的体积是,高是,则它的底面半径是 .
5.将一个两条直角边分别为和的直角三角形绕较长的那条直角边旋转一周,将得到一个 ,这个图形的体积是 .
6.把一个圆柱削成一个最大的圆锥体,已知削去的部分是6立方分米,这个圆柱体的体积是 .
7.一个圆柱的体积是,3个与它等底、等高的圆锥的总体积是 .
二、选择题
1.一个圆柱的底面直径与一个圆锥的底面半径都是10厘米,如果它们的体积也相等,圆柱的高是圆锥的
A.
B.
C.
2.用24个铁圆锥,可以熔铸成 个等底等高的铁圆柱.
A.12
B.8
C.6
D.4
3.把一个圆柱削成一个与它等底等高的圆锥,削去的体积是90立方厘米,这个圆柱的体积是多少立方厘米?列式正确的是
A.
B.
C.
D.
4.若圆柱和圆锥等底等高,且两者体积相差,则圆柱体积是 .
A.28.8
B.14.4
C.48
D.3.2
5.李明拿了等底等高的圆锥和圆柱形容器各一个,他将圆柱形容器装满水后倒入圆锥形容器.当水全部倒完后,发现从圆锥形容器内溢出36.2毫升水.这时,圆锥形容器内还有水 毫升.
A.36.2
B.54.3
C.18.1
D.108.6
6.长方体、正方体、圆柱和圆锥的底面积和高相等,下列说法错误的是
A.长方体、正方体和圆柱的体积相等
B.正方体体积是圆锥体积的3倍
C.圆锥体积是圆柱体积的
D.长方体、正方体和圆柱的表面积相等
7.一个底面半径是10厘米的圆锥,它的高如果增加3厘米,它的体积将会增加 立方厘米.
A.3.14
B.78.5
C.314
D.7.85
8.一个圆锥和一个圆柱的高相等,若要使体积一样,圆锥底面积应是圆柱底面积的
A.3倍
B.
C.倍
D.
三、判断题
1.两个圆锥的底面积相等,它们的体积不一定相等.(
)
2.圆柱的体积一定比圆锥的体积大,圆锥的体积一定比圆柱的体积小.(
)
3.把一根圆柱形木棍削成一个同底等高的圆锥,削去部分占圆柱体积的,圆锥的体积相当于削去部分体积的.(
)
4.等底等体积的一个圆锥和一个圆柱,圆锥的高为6米,那么圆柱的高是18米.(
)
5.圆锥的底面积不变,高扩大为原来的6倍,则体积扩大为原来的2倍.(
)
6.两个圆锥的底和高各不相等,则两个圆锥的体积也一定不相等.(
)
四、计算题
1.计算圆锥的体积.
2.已知:直角三角形如图所示,若以为轴旋转一周得一个几何体,求这个几何体的体积.
五、应用题
1.有一堆混凝土呈圆锥形,底面半径为10米,高3米,用它在东庄修一条宽4米,厚0.2米的水泥路,能修多长?(得数保留整数)
2.计算如图圆锥的体积.
3.求出下面圆锥的体积.(单位:厘米)
4.小明为了测量出一个圆锥的体积,按如下的步骤进行了一个实验:
(1)在一个底面直径是8厘米的圆柱形玻璃杯中装入一定量的水,量得水面的高度是5厘米;
(2)将圆锥完全浸入水中,再次测量水面高度是7厘米.如果玻璃的厚度忽略不计,这个圆锥的体积大约是 立方厘米.
5.正方体的体积是360立方厘米,把它削成一个最大的圆锥,这个圆锥的体积是多少立方厘米?
6.将如图这个三角形纸片以所在直线为对称轴高速旋转,我们会看到一个 体,求出这个形体的体积.
7.一个圆锥形的沙石堆,底面积是188.4平方米,高15米.如果用这堆沙石铺路,公路宽10米.沙石厚2分米,能铺多少米长?
8.一个圆柱和一个圆锥的体积和高都相等,圆柱底面积是,圆锥底面积是多少?
9.如图:在长方体容器内装有水,已知容器内壁底面长为25厘米,宽为20厘米,现把小圆柱体和小圆锥体浸没于水中,水面上升了2厘米.如果圆锥和圆柱的底面积相等高也相等,圆维的体积是多少?
答案
一、填空题
1.30.
2.4.
3.37.68、50.24.
4.20.
5.圆锥、301.44.
6.9立方分米.
7.24.
二、选择题
1..2..3..4..5..6..7..8..
三、判断题
1..2..3..4..5..6..
四、计算题
1.解:
(立方分米),
答:它的体积是62.8立方分米.
2.解:
答:这个圆锥体的体积是37.68.
五、应用题
1.解:
(米
答:能铺392米长.
2.解:
(立方厘米)
答:圆锥的体积是18.84立方厘米.
3.解:
(立方厘米),
答:这个圆锥的体积是25.12立方厘米.
4.解:
(立方厘米)
答:这个圆锥的体积大约是100.48立方厘米.
故答案为:100.48.
5.解:设正方体的棱长为厘米,正方体的体积是,
圆锥的体积:(立方厘米),
答:这个圆锥的体积是94.2立方厘米.
6.解:将如图这个三角形纸片以所在直线为对称轴高速旋转,我们会看到一个
圆锥体,
体积是:
(立方厘米)
答:这个圆锥体的体积是37.68立方厘米.
故答案为:圆锥.
7.解:2分米米
(米
答:能铺471米长.
8.解:(平方厘米),
答:圆锥的底面积是36平方厘米.
故答案为:36.
9.解:圆锥和圆柱的体积和:
(立方厘米);
(立方厘米),
答:圆锥体的体积是250立方厘米.
一、填空题
1.一个圆锥体积是,底面积是,高是 .
2.在下面两个空容器中,将甲容器注满水,再倒入乙容器,这时乙容器中的水深 .
3.一个直角三角形的三条边长分别是、和,若以直角边为轴旋转一圈,旋转一圈形成的图形体积是 立方厘米.取
4.一个圆柱的体积是,高是,则它的底面半径是 .
5.将一个两条直角边分别为和的直角三角形绕较长的那条直角边旋转一周,将得到一个 ,这个图形的体积是 .
6.把一个圆柱削成一个最大的圆锥体,已知削去的部分是6立方分米,这个圆柱体的体积是 .
7.一个圆柱的体积是,3个与它等底、等高的圆锥的总体积是 .
二、选择题
1.一个圆柱的底面直径与一个圆锥的底面半径都是10厘米,如果它们的体积也相等,圆柱的高是圆锥的
A.
B.
C.
2.用24个铁圆锥,可以熔铸成 个等底等高的铁圆柱.
A.12
B.8
C.6
D.4
3.把一个圆柱削成一个与它等底等高的圆锥,削去的体积是90立方厘米,这个圆柱的体积是多少立方厘米?列式正确的是
A.
B.
C.
D.
4.若圆柱和圆锥等底等高,且两者体积相差,则圆柱体积是 .
A.28.8
B.14.4
C.48
D.3.2
5.李明拿了等底等高的圆锥和圆柱形容器各一个,他将圆柱形容器装满水后倒入圆锥形容器.当水全部倒完后,发现从圆锥形容器内溢出36.2毫升水.这时,圆锥形容器内还有水 毫升.
A.36.2
B.54.3
C.18.1
D.108.6
6.长方体、正方体、圆柱和圆锥的底面积和高相等,下列说法错误的是
A.长方体、正方体和圆柱的体积相等
B.正方体体积是圆锥体积的3倍
C.圆锥体积是圆柱体积的
D.长方体、正方体和圆柱的表面积相等
7.一个底面半径是10厘米的圆锥,它的高如果增加3厘米,它的体积将会增加 立方厘米.
A.3.14
B.78.5
C.314
D.7.85
8.一个圆锥和一个圆柱的高相等,若要使体积一样,圆锥底面积应是圆柱底面积的
A.3倍
B.
C.倍
D.
三、判断题
1.两个圆锥的底面积相等,它们的体积不一定相等.(
)
2.圆柱的体积一定比圆锥的体积大,圆锥的体积一定比圆柱的体积小.(
)
3.把一根圆柱形木棍削成一个同底等高的圆锥,削去部分占圆柱体积的,圆锥的体积相当于削去部分体积的.(
)
4.等底等体积的一个圆锥和一个圆柱,圆锥的高为6米,那么圆柱的高是18米.(
)
5.圆锥的底面积不变,高扩大为原来的6倍,则体积扩大为原来的2倍.(
)
6.两个圆锥的底和高各不相等,则两个圆锥的体积也一定不相等.(
)
四、计算题
1.计算圆锥的体积.
2.已知:直角三角形如图所示,若以为轴旋转一周得一个几何体,求这个几何体的体积.
五、应用题
1.有一堆混凝土呈圆锥形,底面半径为10米,高3米,用它在东庄修一条宽4米,厚0.2米的水泥路,能修多长?(得数保留整数)
2.计算如图圆锥的体积.
3.求出下面圆锥的体积.(单位:厘米)
4.小明为了测量出一个圆锥的体积,按如下的步骤进行了一个实验:
(1)在一个底面直径是8厘米的圆柱形玻璃杯中装入一定量的水,量得水面的高度是5厘米;
(2)将圆锥完全浸入水中,再次测量水面高度是7厘米.如果玻璃的厚度忽略不计,这个圆锥的体积大约是 立方厘米.
5.正方体的体积是360立方厘米,把它削成一个最大的圆锥,这个圆锥的体积是多少立方厘米?
6.将如图这个三角形纸片以所在直线为对称轴高速旋转,我们会看到一个 体,求出这个形体的体积.
7.一个圆锥形的沙石堆,底面积是188.4平方米,高15米.如果用这堆沙石铺路,公路宽10米.沙石厚2分米,能铺多少米长?
8.一个圆柱和一个圆锥的体积和高都相等,圆柱底面积是,圆锥底面积是多少?
9.如图:在长方体容器内装有水,已知容器内壁底面长为25厘米,宽为20厘米,现把小圆柱体和小圆锥体浸没于水中,水面上升了2厘米.如果圆锥和圆柱的底面积相等高也相等,圆维的体积是多少?
答案
一、填空题
1.30.
2.4.
3.37.68、50.24.
4.20.
5.圆锥、301.44.
6.9立方分米.
7.24.
二、选择题
1..2..3..4..5..6..7..8..
三、判断题
1..2..3..4..5..6..
四、计算题
1.解:
(立方分米),
答:它的体积是62.8立方分米.
2.解:
答:这个圆锥体的体积是37.68.
五、应用题
1.解:
(米
答:能铺392米长.
2.解:
(立方厘米)
答:圆锥的体积是18.84立方厘米.
3.解:
(立方厘米),
答:这个圆锥的体积是25.12立方厘米.
4.解:
(立方厘米)
答:这个圆锥的体积大约是100.48立方厘米.
故答案为:100.48.
5.解:设正方体的棱长为厘米,正方体的体积是,
圆锥的体积:(立方厘米),
答:这个圆锥的体积是94.2立方厘米.
6.解:将如图这个三角形纸片以所在直线为对称轴高速旋转,我们会看到一个
圆锥体,
体积是:
(立方厘米)
答:这个圆锥体的体积是37.68立方厘米.
故答案为:圆锥.
7.解:2分米米
(米
答:能铺471米长.
8.解:(平方厘米),
答:圆锥的底面积是36平方厘米.
故答案为:36.
9.解:圆锥和圆柱的体积和:
(立方厘米);
(立方厘米),
答:圆锥体的体积是250立方厘米.
