2012年中考复习一轮材料征集:第34课 锐角三角函数和解直角三角形
文档属性
| 名称 | 2012年中考复习一轮材料征集:第34课 锐角三角函数和解直角三角形 |
|
|
| 格式 | zip | ||
| 文件大小 | 282.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-03 00:00:00 | ||
图片预览





文档简介
第34课 锐角三角函数和解直角三角形
山东 赵玉霞
第一部分 讲解部分
(一)课标要求
1、理解锐角三角函数的定义。
2、记住特殊角的三角函数值。
3、会解直角三角形。
(二)知识要点
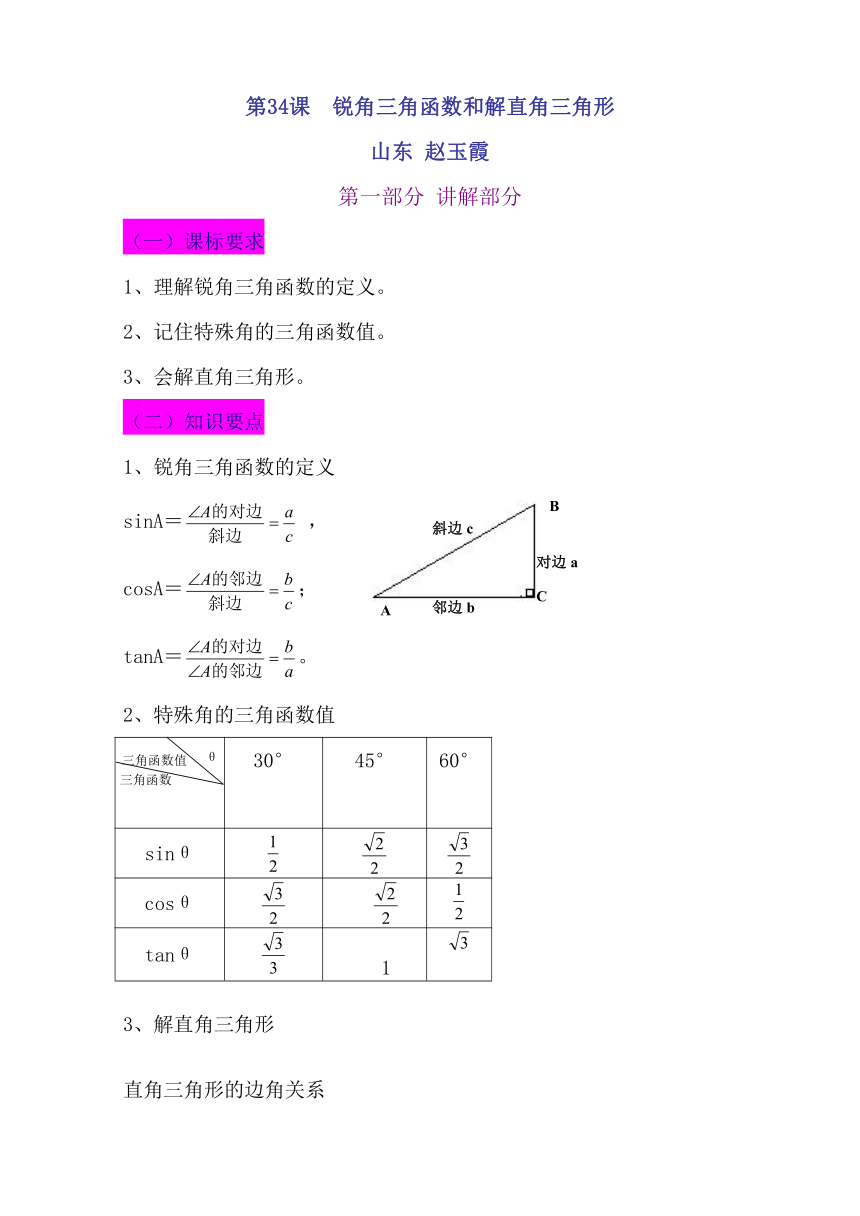
1、锐角三角函数的定义
sinA= ,
cosA=;
tanA=。
2、特殊角的三角函数值
30° 45° 60°
sinθ
cosθ
tanθ 1
3、解直角三角形
直角三角形的边角关系
(1) 两锐角互余:∠A+∠B=90°
(2) 三边满足勾股定理:a2+b2=c2
(3) 边与角的关系:
sinA=cosB=
cosA=sinB=
tanA=cotB=
cotA=tanB=
(三)考点精讲
考点一 :锐角三角函数的定义
(1)锐角三角函数定义
1.(浙江温州4分)如图,在△ABC中,∠C=90°,AB=13,BC=5,则sinA的值是
A、 B、 C、 D、
【答案】A。
【考点】锐角三角函数的定义。
【分析】直接利用锐角三角函数的定义求解,sinA为∠A的对边比斜边,求出即可:sinA=。故选A。
【点评】这类题目只要分清是应用哪个三角函数,对号入座即可。
(2)锐角三角函数和其他知识点的综合应用。
2.(广西桂林3分)如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为
A、 B、 C、 D、
【答案】C。
【考点】勾股定理,锐角三角函数的定义。
【分析】直角三角形中,正弦值是角的对边与斜边的比值;先求出斜边AB的值,然后,即可解答:
∵Rt△ABC中,∠C=90°,BC=3,AC=4,∴AB==5。
∴sinA=。故选C。
【点评】这类题目首先看一下要求哪个三角函数,找好所对应的边,对于没直接给出的考虑用勾股定理来解决。
3.(贵州安顺4分)如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦.则tan∠OBE= .
【答案】。
【考点】圆周角定理,坐标与图形性质,锐角三角函数的定义。
【分析】连接EC,根据同弧所对的圆周角相等,得∠ECO=∠OBE。由锐角三角函数可求tan∠ECO=,即tan∠OBE=。
【点评】本题要求的三角函数不在直角三角形中,所以应想到如何将要求的角放到直角三角形中,这也是辅助线的做法。所以构造直角三角形来解决三角函数是关键。
4.(江苏连云港3分)△ABC的顶点都在方格纸的格点上,则sinA=_ .
【答案】。
【考点】锐角三角函数的定义,勾股定理,二次根式化简。
【分析】。
【点评】本题是格点三角形中求三角函数值。应把要求的角放到直角三角形中,利用格点求所用的边。
5.(云南昆明3分)如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线与D点,垂足为E,则sin∠CAD=
A、 QUOTE B、 C、 D、
【答案】A。
【考点】锐角三角函数的定义,线段垂直平分线的性质,勾股定理。
【分析】设AD=x,则CD=x-3,
在直角△ACD中,(x-3)2+ ()2=x2,解得,x=4。
∴CD=4-3=1,∴sin∠CAD=。故选A。
【点评】本题是要求的三角函数已经在直角三角形中,但边不明确。这就要用到已知中的条件,垂直平分线上的点到线段两端点的距离相等,通过设未知数,勾股定理,来求出所用的两边。
考点二 :特殊角的三角函数值
6.(广西玉林、防城港3分)若∠α的余角是30°,则cosα的值是
A、 B、 C、 D、
【答案】A。
【考点】余角的概念,特殊角的三角函数。
【分析】先根据题意求得α的值,再求它的余弦值:∠α=90°-30°=60°,cosα=cos60°= .故选A。
【点评】这类题目关键是记熟特殊角的三角函数值。
7.(四川遂宁4分)计算2sin30-sin45+cot60的结果
A. B. C. D.
【答案】B。
【考点】特殊角的三角函数值,二次根式计算。
【分析】分别把sin30°的值,sin45°的值,cot60°的值代入进行计算即可:
2sin-sin245°+cot60°=。故选B。
【点评】熟练记住特殊角的三角函数值,并能进行熟练的二次根式计算。
考点三:解直角三角形
8.(湖北宜昌3分)如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=,则边BC的长为
A. 30 cm B. 20 cm C. 10 cm D. 5 cm
【答案】C。
【考点】解直角三角形,特殊角的三角函数值。
【分析】在Rt△ABC中,根据三角函数定义可求:∵tan∠BAC=,又AC=30cm,tan∠BAC=,∴BC=AC·tan∠BAC=30×=10cm。故选C。
【点评】这是解直角三角形的直接应用。在直角三角形中。有三角函数及一边,求另一边,对号入座即可。
9.(山东临沂3分)如图,△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是
A、 B、12 C、14 D、21
【答案】A。
【考点】解直角三角形。
【分析】根据已知做出三角形的高线AD,进而得出AD,BD,CD,的长,即可得出三角形的面积:过点A做AD⊥BC,∵△ABC中,cosB=,sinC=,AC=5,∴cosB=,∴∠B=45°。
∵sinC=,∴AD=3,∴CD=4,∴BD=3,则△ABC的面积是:×AD×BC=×3×(3+4)=。故选A。
【点评】本题出现了三角函数,所以应构造直角三角形;求面积,要用到高,故本题的辅助线一定是做高。这也是解直角三角形中常见的题目,是重点也是难点。辅助线一定要把握好,一般说来要把已知和求中的三角函数、角放到直角三角形中。
(四)易错点剖析
易错点一:混淆定义
1. (山东日照4分)在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cotA=.则下列关系式中不成立的是
A、tanA·cotA=1 B、sinA=tanA·cosA
C、cosA=cotA·sinA D、tan2A+cot2A=1
【答案】D。
【考点】三角函数的定义,代数式变换。
【分析】根据三角函数的定义和已知cotA=,逐一计算进行判断;A、tanA·cotA==1,关系式成立;B、∵左边=sinA=,右边=tanA·cosA==,∴左边=右边,关系式成立;C、∵左边=cosA=,右边=cotA·sinA==,∴左边=右边,关系式成立; D、tan2A+cot2A=≠1,关系式不成立。故选D。
易错点二:问题考虑不全面
2.(山东烟台4分)如果△ABC中,sinA=cosB=,则下列最确切的结论是
A. △ABC是直角三角形 B. △ABC是等腰三角形
C. △ABC是等腰直角三角形 D. △ABC是锐角三角形
【答案】C
【考点】特殊角的三角函数值,三角形分类。
【分析】∵sinA=cosB=,∴∠A=∠B=45°,∴△ABC是等腰直角三角形。故选C。
易错点三:
解非直角三角形时,辅助线不能很好的把握,导致整个题目不得分,找不到明确的思路。
易混点一:
对特殊角的三角函数值不能熟练掌握,张冠李戴,似是而非。导致计算错误。
(五)真题演练
1.(浙江湖州3分)如图,在△ABC中,∠C=90 ,BC=1,AC=2,则tanA的值为
A.2 B. C. EQ \F(,5) D. EQ \F(2,5)
2.(广西贵港3分)如图所示,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,AD=2,则tan∠CAD的值是
A.2 B. C. D.
3.(湖北荆州3分)在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是
A. B. C. D.
4.(黑龙江龙东五市3分)已知等腰三角形两边长分别为5和8,则底角的余弦值为 。
5.(黑龙江大庆3分)计算:sin230 +cos260 -tan245 = .
6.(甘肃兰州 8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据: ( http: / / www.21cnjy.com )≈1.41,≈1.73, ( http: / / www.21cnjy.com )≈2.24,≈2.45)
7.(珠海7分)如图,在鱼塘两侧有两棵树A、B,小华要测量此两树之间的距离.他在距A树30 m的C处测得∠ACB=30°,又在B处测得∠ABC=120°.求A、B两树之间的距离
(结果精确到0.1m)(参考数据:≈1.414,≈1.732)
第二部分 练习部分
1.(广西来宾3分)在Rt△ABC中,∠C=90°,AB=5,BC=3,则∠A的余弦值为
A、 B、 C、 D、
2. (陕西省3分)在△ABC中,若三边BC,CA,AB满足BC:CA:AB=5:12:13,则cosB=
A. B. C. D.
3.(贵州黔东南4分)如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,若BC=6,AC=8,则tan∠ACD的值为
A、 B、 C、
D、
4.(江苏南京2分)如图,以O为圆心,任意长为半径画弧,与射线OM交
于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则
cos∠AOB的值等于 .
5.(重庆綦江县)据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒= HYPERLINK " http://www.21cnjy.com" 小时),并测得∠PAO=59°,∠BPO=45°.
试计算AB并判断此车是否超速?(精确到0.001).
(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
6.(广西南宁)某厂房屋顶呈人字架形(等腰三角形),如图8所示,
已知, HYPERLINK " http://www.21cnjy.com" ,于点 HYPERLINK " http://www.21cnjy.com" .
求的大小;
求 HYPERLINK " http://www.21cnjy.com" 的长度.
7.(湖北宜昌)如图,华庆号船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且。
(1)求这时船A与海岛B之间的距离;
(2)若海岛B周围16海里内有海礁,华庆号船继续沿AC向C航行有无触礁危险?请说明理由(7分)
( http: / / www.21cnjy.com )
8.(连云港10分)如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).(参考数据:≈1.73,sin74°≈,
cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
9、(北京)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
★“真题演练”答案★
1、解答:根据正切函数的定义,tanA=。故选B。
2、解答:由AD是BC边上的中线,BD=4,得 DC=4。又在△ABC中,∠C=90°,AD=2,DC=4,由勾股定理得AC=,tan∠CAD=。故选A。
3、解答:作CD⊥BD,交BA的延长线于D,
∵∠A=120°,AB=4,AC=2,∴∠DAC=60°,∠ACD=30°。
∴2AD=AC=2。∴AD=1,CD=。∴BD=5,∴BC=2。
∴sinB= 。故选D。
4、解答:先确定等腰三角形的腰长和底边长,分两种情况讨论,当底边长为5和底边长为8时,作底边的高,构成直角三角形,然后根据锐角三角函数的定义求解:当腰长为5,底边长8时,作底边的高,则底角的余弦=;当腰长为8,底边长5时,作底边的高,则底角的余弦=。
5、解答:把三角函数的数值代入计算即可:sin230 +cos260 -tan245 =。
6、解答:(1)如图,作AD⊥BC于点D
Rt△ABD中,
AD=ABsin45°=4 ( http: / / www.21cnjy.com )……2分
在Rt△ACD中,∵∠ACD=30°
∴AC=2AD=≈ ( http: / / www.21cnjy.com )
即新传送带AC的长度约为米.
(2)结论:货物MNQP应挪走.
解:在Rt△ABD中,BD=ABcos45°=4 ( http: / / www.21cnjy.com )
在Rt△ACD中,CD=AC cos30°=
∴CB=CD—BD= ( http: / / www.21cnjy.com )≈2.1
∵PC=PB—CB ≈4—2.1=1.9<2
∴货物MNQP应挪走.
7、解答:解:作BD⊥AC,垂足为点D 。
∵∠C=30°,∠ABC=120°,∴∠A=30°。
∴AB=BC 。∴AD=CD=AC=×30=15 。
在Rt△ABD中,∵cosA=,
∴ AB==。
答:A、B两树之间的距离约为17.3m。
“练习部分”答案★
1、解答:根据勾股定理,求出AC,从而由余弦=邻边÷斜边得:
cosA 。 故选C。
2、解答:∵BC,CA,AB满足BC:CA:AB=5:12:13,而52+122=132,即BC2+CA2=AB2,
∴根据勾股定理的逆定理,得△ABC是直角三角形,且AB是斜边。
∴cosB=。故选C。
3、解答:延长CD于点E,使DE=CD,连接AE,BE。则
∵DE=CD,AD=DE,∴四边形ACBE是平行四边形(对角线互相平分的四边形是平行四边形)。
又∵∠ACB=90°,∴四边形ACBE是矩形(有一个角是直角的平行四边形是矩形)。
∴∠CAE=90°(矩形四个角是直角),AE=BC=6。
∴在Rt△CAE中,由正切函数的定义,tan∠ACD=tan∠ACE=。故选D。
4、解答:由已知,O、A、B三点构成的三角形是等边三角形,根据等边三角形每个内角等于600的性质得
cos∠AOB=cos600=。
5、解答:设该轿车的速度为每小时v千米
∵AB=AO-BO,∠BPO=45°
∴BO=PO=0.1千米
又AO=OP×tan59°=0.1×1.6643
∴AB=AO-BO=0.1×1.6643-0.1=0.1×0.6643=0.06643
即AB≈0.0066千米
而3秒= HYPERLINK " http://www.21cnjy.com" 小时
∴v=0.06643×1200≈79.716千米/小时
∵79.716<80
∴该轿车没有超速.
6、解答:解:(1)∵ HYPERLINK " http://www.21cnjy.com"
∴
∵ HYPERLINK " http://www.21cnjy.com"
∴
HYPERLINK " http://www.21cnjy.com"
(2)∵ HYPERLINK " http://www.21cnjy.com" ∴
在 HYPERLINK " http://www.21cnjy.com" 中,, HYPERLINK " http://www.21cnjy.com"
∴
HYPERLINK " http://www.21cnjy.com"
∴( HYPERLINK " http://www.21cnjy.com" )
7、解答:(1)证明:∵∠CBA=30°, ∠CAB=60°,90°.
在Rt△ACB中, ∵ HYPERLINK " http://www.21cnjy.com" ,.
(2)在Rt△ACB中,tan60°= HYPERLINK " http://www.21cnjy.com" , ,
HYPERLINK " http://www.21cnjy.com" (或BC≈17>16).
答:无触礁危险.
8、解答: (1)相等
又
在与△ABF中
(2)法一:作,垂足为H 设 AE=x
则AH=xsin74°HE= xcos74°
HF= xcos74°+1
所以xsin74°=(xcos74°+1)tan60°
即0.96x=(0.28x+1)×1.73
所以
即AB
答: 两个岛屿A与B之间的距离约为3.6km
法二:设AF与BE的交点为G,在Rt△EGF中,因为EF=1,
所以 EG=
在Rt△AEG中
答: 两个岛屿A与B之间的距离约为3.6km
9、解答:解:(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=∠CAB.
∵∠CBF=∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)过点C作CG⊥AB于点G.
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1=
∵∠AEB=90°,AB=5,
∴BE=AB sin∠1=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE=2,
∴sin∠2=,cos∠2=,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△BFA
∴
∴BF==
A
邻边b
C
对边a
B
斜边c
三角函数值
三角函数
θ
C
B
A
C
B
A
AD
BAD
EBAD
FEBAD
QFEBAD
PQFEBAD
C
B
A
D
山东 赵玉霞
第一部分 讲解部分
(一)课标要求
1、理解锐角三角函数的定义。
2、记住特殊角的三角函数值。
3、会解直角三角形。
(二)知识要点
1、锐角三角函数的定义
sinA= ,
cosA=;
tanA=。
2、特殊角的三角函数值
30° 45° 60°
sinθ
cosθ
tanθ 1
3、解直角三角形
直角三角形的边角关系
(1) 两锐角互余:∠A+∠B=90°
(2) 三边满足勾股定理:a2+b2=c2
(3) 边与角的关系:
sinA=cosB=
cosA=sinB=
tanA=cotB=
cotA=tanB=
(三)考点精讲
考点一 :锐角三角函数的定义
(1)锐角三角函数定义
1.(浙江温州4分)如图,在△ABC中,∠C=90°,AB=13,BC=5,则sinA的值是
A、 B、 C、 D、
【答案】A。
【考点】锐角三角函数的定义。
【分析】直接利用锐角三角函数的定义求解,sinA为∠A的对边比斜边,求出即可:sinA=。故选A。
【点评】这类题目只要分清是应用哪个三角函数,对号入座即可。
(2)锐角三角函数和其他知识点的综合应用。
2.(广西桂林3分)如图,已知Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值为
A、 B、 C、 D、
【答案】C。
【考点】勾股定理,锐角三角函数的定义。
【分析】直角三角形中,正弦值是角的对边与斜边的比值;先求出斜边AB的值,然后,即可解答:
∵Rt△ABC中,∠C=90°,BC=3,AC=4,∴AB==5。
∴sinA=。故选C。
【点评】这类题目首先看一下要求哪个三角函数,找好所对应的边,对于没直接给出的考虑用勾股定理来解决。
3.(贵州安顺4分)如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦.则tan∠OBE= .
【答案】。
【考点】圆周角定理,坐标与图形性质,锐角三角函数的定义。
【分析】连接EC,根据同弧所对的圆周角相等,得∠ECO=∠OBE。由锐角三角函数可求tan∠ECO=,即tan∠OBE=。
【点评】本题要求的三角函数不在直角三角形中,所以应想到如何将要求的角放到直角三角形中,这也是辅助线的做法。所以构造直角三角形来解决三角函数是关键。
4.(江苏连云港3分)△ABC的顶点都在方格纸的格点上,则sinA=_ .
【答案】。
【考点】锐角三角函数的定义,勾股定理,二次根式化简。
【分析】。
【点评】本题是格点三角形中求三角函数值。应把要求的角放到直角三角形中,利用格点求所用的边。
5.(云南昆明3分)如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线与D点,垂足为E,则sin∠CAD=
A、 QUOTE B、 C、 D、
【答案】A。
【考点】锐角三角函数的定义,线段垂直平分线的性质,勾股定理。
【分析】设AD=x,则CD=x-3,
在直角△ACD中,(x-3)2+ ()2=x2,解得,x=4。
∴CD=4-3=1,∴sin∠CAD=。故选A。
【点评】本题是要求的三角函数已经在直角三角形中,但边不明确。这就要用到已知中的条件,垂直平分线上的点到线段两端点的距离相等,通过设未知数,勾股定理,来求出所用的两边。
考点二 :特殊角的三角函数值
6.(广西玉林、防城港3分)若∠α的余角是30°,则cosα的值是
A、 B、 C、 D、
【答案】A。
【考点】余角的概念,特殊角的三角函数。
【分析】先根据题意求得α的值,再求它的余弦值:∠α=90°-30°=60°,cosα=cos60°= .故选A。
【点评】这类题目关键是记熟特殊角的三角函数值。
7.(四川遂宁4分)计算2sin30-sin45+cot60的结果
A. B. C. D.
【答案】B。
【考点】特殊角的三角函数值,二次根式计算。
【分析】分别把sin30°的值,sin45°的值,cot60°的值代入进行计算即可:
2sin-sin245°+cot60°=。故选B。
【点评】熟练记住特殊角的三角函数值,并能进行熟练的二次根式计算。
考点三:解直角三角形
8.(湖北宜昌3分)如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=,则边BC的长为
A. 30 cm B. 20 cm C. 10 cm D. 5 cm
【答案】C。
【考点】解直角三角形,特殊角的三角函数值。
【分析】在Rt△ABC中,根据三角函数定义可求:∵tan∠BAC=,又AC=30cm,tan∠BAC=,∴BC=AC·tan∠BAC=30×=10cm。故选C。
【点评】这是解直角三角形的直接应用。在直角三角形中。有三角函数及一边,求另一边,对号入座即可。
9.(山东临沂3分)如图,△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是
A、 B、12 C、14 D、21
【答案】A。
【考点】解直角三角形。
【分析】根据已知做出三角形的高线AD,进而得出AD,BD,CD,的长,即可得出三角形的面积:过点A做AD⊥BC,∵△ABC中,cosB=,sinC=,AC=5,∴cosB=,∴∠B=45°。
∵sinC=,∴AD=3,∴CD=4,∴BD=3,则△ABC的面积是:×AD×BC=×3×(3+4)=。故选A。
【点评】本题出现了三角函数,所以应构造直角三角形;求面积,要用到高,故本题的辅助线一定是做高。这也是解直角三角形中常见的题目,是重点也是难点。辅助线一定要把握好,一般说来要把已知和求中的三角函数、角放到直角三角形中。
(四)易错点剖析
易错点一:混淆定义
1. (山东日照4分)在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cotA=.则下列关系式中不成立的是
A、tanA·cotA=1 B、sinA=tanA·cosA
C、cosA=cotA·sinA D、tan2A+cot2A=1
【答案】D。
【考点】三角函数的定义,代数式变换。
【分析】根据三角函数的定义和已知cotA=,逐一计算进行判断;A、tanA·cotA==1,关系式成立;B、∵左边=sinA=,右边=tanA·cosA==,∴左边=右边,关系式成立;C、∵左边=cosA=,右边=cotA·sinA==,∴左边=右边,关系式成立; D、tan2A+cot2A=≠1,关系式不成立。故选D。
易错点二:问题考虑不全面
2.(山东烟台4分)如果△ABC中,sinA=cosB=,则下列最确切的结论是
A. △ABC是直角三角形 B. △ABC是等腰三角形
C. △ABC是等腰直角三角形 D. △ABC是锐角三角形
【答案】C
【考点】特殊角的三角函数值,三角形分类。
【分析】∵sinA=cosB=,∴∠A=∠B=45°,∴△ABC是等腰直角三角形。故选C。
易错点三:
解非直角三角形时,辅助线不能很好的把握,导致整个题目不得分,找不到明确的思路。
易混点一:
对特殊角的三角函数值不能熟练掌握,张冠李戴,似是而非。导致计算错误。
(五)真题演练
1.(浙江湖州3分)如图,在△ABC中,∠C=90 ,BC=1,AC=2,则tanA的值为
A.2 B. C. EQ \F(,5) D. EQ \F(2,5)
2.(广西贵港3分)如图所示,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,AD=2,则tan∠CAD的值是
A.2 B. C. D.
3.(湖北荆州3分)在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是
A. B. C. D.
4.(黑龙江龙东五市3分)已知等腰三角形两边长分别为5和8,则底角的余弦值为 。
5.(黑龙江大庆3分)计算:sin230 +cos260 -tan245 = .
6.(甘肃兰州 8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据: ( http: / / www.21cnjy.com )≈1.41,≈1.73, ( http: / / www.21cnjy.com )≈2.24,≈2.45)
7.(珠海7分)如图,在鱼塘两侧有两棵树A、B,小华要测量此两树之间的距离.他在距A树30 m的C处测得∠ACB=30°,又在B处测得∠ABC=120°.求A、B两树之间的距离
(结果精确到0.1m)(参考数据:≈1.414,≈1.732)
第二部分 练习部分
1.(广西来宾3分)在Rt△ABC中,∠C=90°,AB=5,BC=3,则∠A的余弦值为
A、 B、 C、 D、
2. (陕西省3分)在△ABC中,若三边BC,CA,AB满足BC:CA:AB=5:12:13,则cosB=
A. B. C. D.
3.(贵州黔东南4分)如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,若BC=6,AC=8,则tan∠ACD的值为
A、 B、 C、
D、
4.(江苏南京2分)如图,以O为圆心,任意长为半径画弧,与射线OM交
于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则
cos∠AOB的值等于 .
5.(重庆綦江县)据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒= HYPERLINK " http://www.21cnjy.com" 小时),并测得∠PAO=59°,∠BPO=45°.
试计算AB并判断此车是否超速?(精确到0.001).
(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
6.(广西南宁)某厂房屋顶呈人字架形(等腰三角形),如图8所示,
已知, HYPERLINK " http://www.21cnjy.com" ,于点 HYPERLINK " http://www.21cnjy.com" .
求的大小;
求 HYPERLINK " http://www.21cnjy.com" 的长度.
7.(湖北宜昌)如图,华庆号船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且。
(1)求这时船A与海岛B之间的距离;
(2)若海岛B周围16海里内有海礁,华庆号船继续沿AC向C航行有无触礁危险?请说明理由(7分)
( http: / / www.21cnjy.com )
8.(连云港10分)如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).(参考数据:≈1.73,sin74°≈,
cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
9、(北京)如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
★“真题演练”答案★
1、解答:根据正切函数的定义,tanA=。故选B。
2、解答:由AD是BC边上的中线,BD=4,得 DC=4。又在△ABC中,∠C=90°,AD=2,DC=4,由勾股定理得AC=,tan∠CAD=。故选A。
3、解答:作CD⊥BD,交BA的延长线于D,
∵∠A=120°,AB=4,AC=2,∴∠DAC=60°,∠ACD=30°。
∴2AD=AC=2。∴AD=1,CD=。∴BD=5,∴BC=2。
∴sinB= 。故选D。
4、解答:先确定等腰三角形的腰长和底边长,分两种情况讨论,当底边长为5和底边长为8时,作底边的高,构成直角三角形,然后根据锐角三角函数的定义求解:当腰长为5,底边长8时,作底边的高,则底角的余弦=;当腰长为8,底边长5时,作底边的高,则底角的余弦=。
5、解答:把三角函数的数值代入计算即可:sin230 +cos260 -tan245 =。
6、解答:(1)如图,作AD⊥BC于点D
Rt△ABD中,
AD=ABsin45°=4 ( http: / / www.21cnjy.com )……2分
在Rt△ACD中,∵∠ACD=30°
∴AC=2AD=≈ ( http: / / www.21cnjy.com )
即新传送带AC的长度约为米.
(2)结论:货物MNQP应挪走.
解:在Rt△ABD中,BD=ABcos45°=4 ( http: / / www.21cnjy.com )
在Rt△ACD中,CD=AC cos30°=
∴CB=CD—BD= ( http: / / www.21cnjy.com )≈2.1
∵PC=PB—CB ≈4—2.1=1.9<2
∴货物MNQP应挪走.
7、解答:解:作BD⊥AC,垂足为点D 。
∵∠C=30°,∠ABC=120°,∴∠A=30°。
∴AB=BC 。∴AD=CD=AC=×30=15 。
在Rt△ABD中,∵cosA=,
∴ AB==。
答:A、B两树之间的距离约为17.3m。
“练习部分”答案★
1、解答:根据勾股定理,求出AC,从而由余弦=邻边÷斜边得:
cosA 。 故选C。
2、解答:∵BC,CA,AB满足BC:CA:AB=5:12:13,而52+122=132,即BC2+CA2=AB2,
∴根据勾股定理的逆定理,得△ABC是直角三角形,且AB是斜边。
∴cosB=。故选C。
3、解答:延长CD于点E,使DE=CD,连接AE,BE。则
∵DE=CD,AD=DE,∴四边形ACBE是平行四边形(对角线互相平分的四边形是平行四边形)。
又∵∠ACB=90°,∴四边形ACBE是矩形(有一个角是直角的平行四边形是矩形)。
∴∠CAE=90°(矩形四个角是直角),AE=BC=6。
∴在Rt△CAE中,由正切函数的定义,tan∠ACD=tan∠ACE=。故选D。
4、解答:由已知,O、A、B三点构成的三角形是等边三角形,根据等边三角形每个内角等于600的性质得
cos∠AOB=cos600=。
5、解答:设该轿车的速度为每小时v千米
∵AB=AO-BO,∠BPO=45°
∴BO=PO=0.1千米
又AO=OP×tan59°=0.1×1.6643
∴AB=AO-BO=0.1×1.6643-0.1=0.1×0.6643=0.06643
即AB≈0.0066千米
而3秒= HYPERLINK " http://www.21cnjy.com" 小时
∴v=0.06643×1200≈79.716千米/小时
∵79.716<80
∴该轿车没有超速.
6、解答:解:(1)∵ HYPERLINK " http://www.21cnjy.com"
∴
∵ HYPERLINK " http://www.21cnjy.com"
∴
HYPERLINK " http://www.21cnjy.com"
(2)∵ HYPERLINK " http://www.21cnjy.com" ∴
在 HYPERLINK " http://www.21cnjy.com" 中,, HYPERLINK " http://www.21cnjy.com"
∴
HYPERLINK " http://www.21cnjy.com"
∴( HYPERLINK " http://www.21cnjy.com" )
7、解答:(1)证明:∵∠CBA=30°, ∠CAB=60°,90°.
在Rt△ACB中, ∵ HYPERLINK " http://www.21cnjy.com" ,.
(2)在Rt△ACB中,tan60°= HYPERLINK " http://www.21cnjy.com" , ,
HYPERLINK " http://www.21cnjy.com" (或BC≈17>16).
答:无触礁危险.
8、解答: (1)相等
又
在与△ABF中
(2)法一:作,垂足为H 设 AE=x
则AH=xsin74°HE= xcos74°
HF= xcos74°+1
所以xsin74°=(xcos74°+1)tan60°
即0.96x=(0.28x+1)×1.73
所以
即AB
答: 两个岛屿A与B之间的距离约为3.6km
法二:设AF与BE的交点为G,在Rt△EGF中,因为EF=1,
所以 EG=
在Rt△AEG中
答: 两个岛屿A与B之间的距离约为3.6km
9、解答:解:(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=∠CAB.
∵∠CBF=∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)过点C作CG⊥AB于点G.
∵sin∠CBF=,∠1=∠CBF,
∴sin∠1=
∵∠AEB=90°,AB=5,
∴BE=AB sin∠1=,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE=2,
∴sin∠2=,cos∠2=,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△BFA
∴
∴BF==
A
邻边b
C
对边a
B
斜边c
三角函数值
三角函数
θ
C
B
A
C
B
A
AD
BAD
EBAD
FEBAD
QFEBAD
PQFEBAD
C
B
A
D
同课章节目录
