2012年中考复习一轮材料征集:第21课时 直角三角形
文档属性
| 名称 | 2012年中考复习一轮材料征集:第21课时 直角三角形 |

|
|
| 格式 | zip | ||
| 文件大小 | 231.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-03 00:00:00 | ||
图片预览


文档简介
第21课时 直角三角形
西安市西光中学 贾文 陈伟伦
第一部分
一 讲解
1 了解认识直角三角形的概念(基本特征,直角等)
2 理解掌握直角三角形的判断与其性质(勾股定理,斜边与直角边关系等)
3 灵活运用勾股定理解决简单问题
4 体验勾股定理的探索过程
5探索直角三角形的判断与其性质(尝试自己推导有关直角三角形的性质)
二 知识点
知识点一 直角三角形的基本性质
1直角三角形的两个锐角互余
可表示如下:∠C=90°∠A+∠B=90°
2在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30°
可表示如下: BC=AB
∠C=90°
3、直角三角形斜边上的中线等于斜边的一半
∠ACB=90°
可表示如下: CD=AB=BD=AD
D为AB的中点
4、勾股定理
直角三角形两直角边a,b的平方和等于斜边c的平方,即
5、母子相似定理(射影定理)
在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项
∠ACB=90°
CD⊥AB
6、常用关系式
由三角形面积公式可得:
ABCD=ACBC
知识点二 直角三角形的判定
1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、勾股定理的逆定理
如果三角形的三边长a,b,c有关系,那么这个三角形是直角三角形。
知识点三 锐角三角函数的概念
1、如图,在△ABC中,∠C=90°
①锐角A的对边与斜边的比叫做∠A的正弦,记为sinA,即
②锐角A的邻边与斜边的比叫做∠A的余弦,记为cosA,即
③锐角A的对边与邻边的比叫做∠A的正切,记为tanA,即
④锐角A的邻边与对边的比叫做∠A的余切,记为cotA,即
2、锐角三角函数的概念
锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数
3、一些特殊角的三角函数值
三角函数 0° 30° 45° 60° 90°
sinα 0 1
cosα 1 0
tanα 0 1 不存在
cotα 不存在 1 0
4、各锐角三角函数之间的关系
(1)互余关系
sinA=cos(90°—A),cosA=sin(90°—A)
tanA=cot(90°—A),cotA=tan(90°—A)
(2)平方关系
(3)倒数关系
tanAtan(90°—A)=1
(4)弦切关系
tanA=
知识点四 勾股定理中的方程思想
1.水中草问题
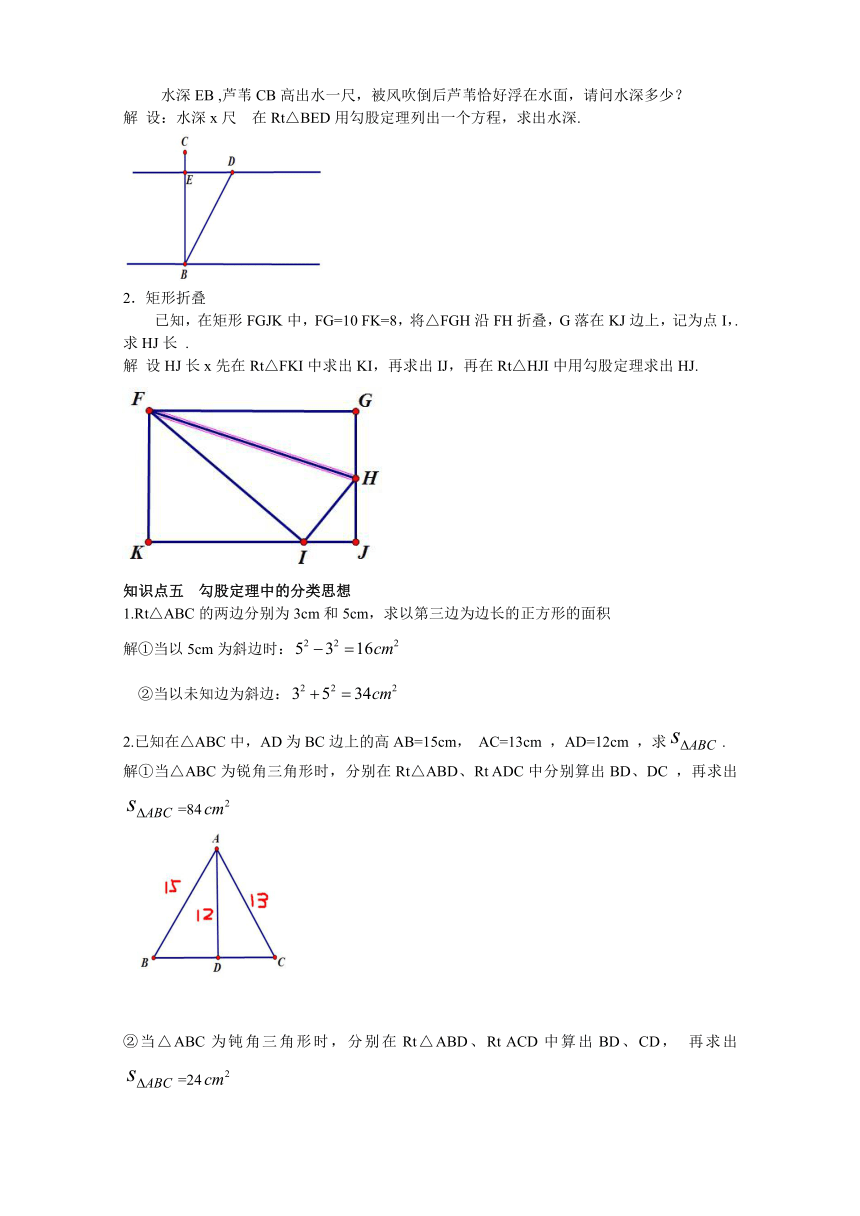
水深EB ,芦苇CB高出水一尺,被风吹倒后芦苇恰好浮在水面,请问水深多少?
解 设:水深x尺 在Rt△BED用勾股定理列出一个方程,求出水深.
2.矩形折叠
已知,在矩形FGJK中,FG=10 FK=8,将△FGH沿FH折叠,G落在KJ边上,记为点I,.求HJ长 .
解 设HJ长x先在Rt△FKI中求出KI,再求出IJ,再在Rt△HJI中用勾股定理求出HJ.
知识点五 勾股定理中的分类思想
1.Rt△ABC的两边分别为3cm和5cm,求以第三边为边长的正方形的面积
解①当以5cm为斜边时:
②当以未知边为斜边:
已知在△ABC中,AD为BC边上的高AB=15cm, AC=13cm ,AD=12cm ,求.
解①当△ABC为锐角三角形时,分别在Rt△ABD、Rt ADC中分别算出BD、DC ,再求出=84
②当△ABC为钝角三角形时,分别在Rt△ABD、Rt ACD中算出BD、CD, 再求出=24
知识点六 三维空间中的勾股定理
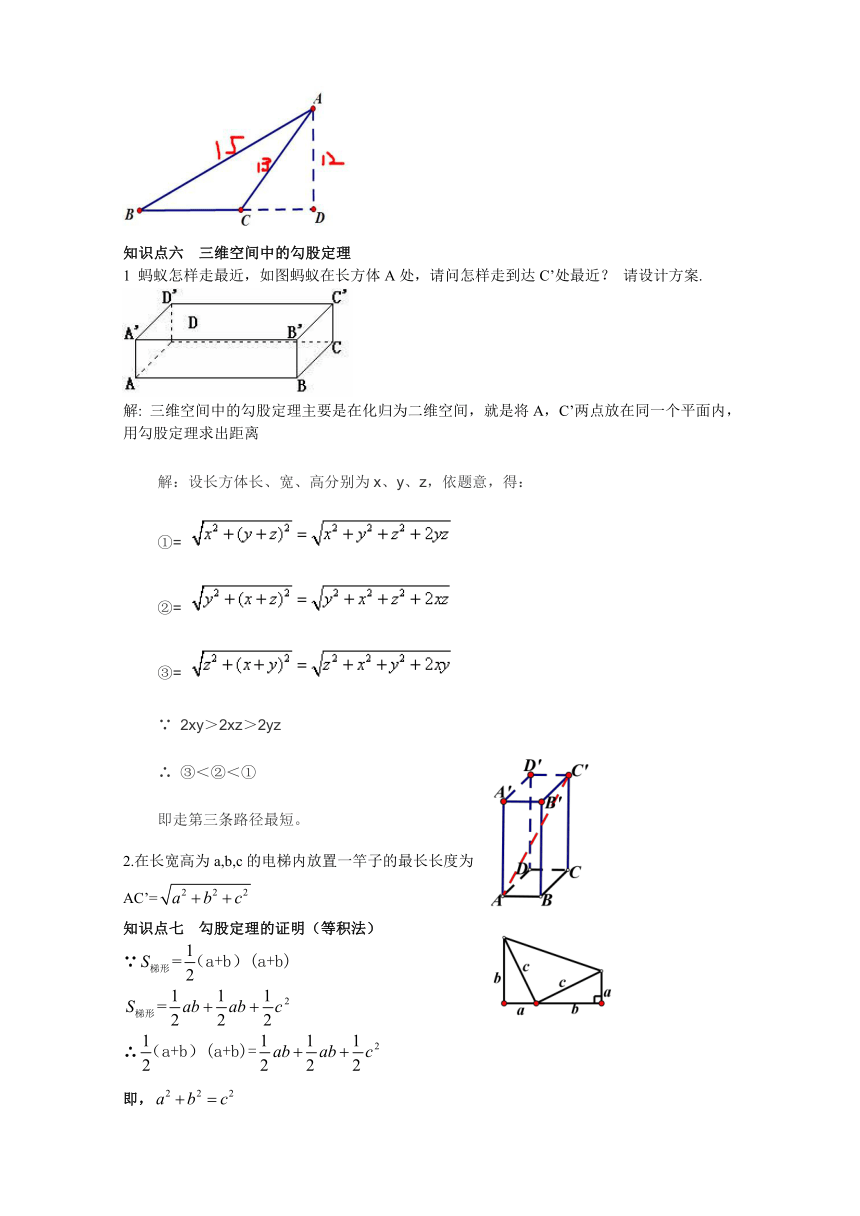
1 蚂蚁怎样走最近,如图蚂蚁在长方体A处,请问怎样走到达C’处最近? 请设计方案.
解: 三维空间中的勾股定理主要是在化归为二维空间,就是将A,C’两点放在同一个平面内,用勾股定理求出距离
解:设长方体长、宽、高分别为x、y、z,依题意,得:
①=
②=
③=
∵ 2xy>2xz>2yz
∴ ③<②<①
即走第三条路径最短。
2.在长宽高为a,b,c的电梯内放置一竿子的最长长度为
AC’=
知识点七 勾股定理的证明(等积法)
∵
∴
即,
三 考点精讲
例题一
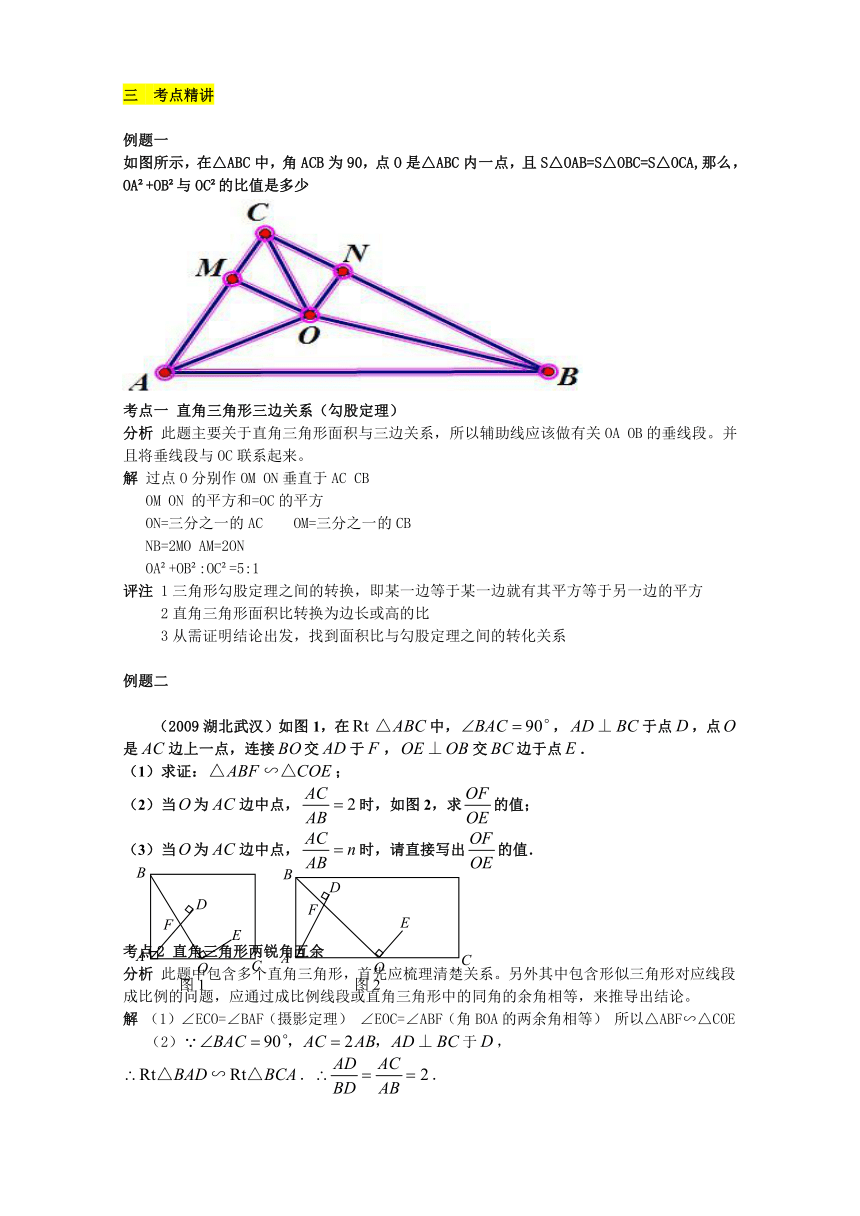
如图所示,在△ABC中,角ACB为90,点O是△ABC内一点,且S△OAB=S△OBC=S△OCA,那么,OA +OB 与OC 的比值是多少
考点一 直角三角形三边关系(勾股定理)
分析 此题主要关于直角三角形面积与三边关系,所以辅助线应该做有关OA OB的垂线段。并且将垂线段与OC联系起来。
解 过点O分别作OM ON垂直于AC CB
OM ON 的平方和=OC的平方
ON=三分之一的AC OM=三分之一的CB
NB=2MO AM=2ON
OA +OB :OC =5:1
评注 1三角形勾股定理之间的转换,即某一边等于某一边就有其平方等于另一边的平方
2直角三角形面积比转换为边长或高的比
3从需证明结论出发,找到面积比与勾股定理之间的转化关系
例题二
(2009湖北武汉)如图1,在中,,于点,点是边上一点,连接交于,交边于点.
(1)求证:;
(2)当为边中点,时,如图2,求的值;
(3)当为边中点,时,请直接写出的值.
考点2 直角三角形两锐角互余
分析 此题中包含多个直角三角形,首先应梳理清楚关系。另外其中包含形似三角形对应线段成比例的问题,应通过成比例线段或直角三角形中的同角的余角相等,来推导出结论。
解 (1)∠ECO=∠BAF(摄影定理) ∠EOC=∠ABF(角BOA的两余角相等) 所以△ABF∽△COE
(2)于,
..
设,则,
.
,
.
由(1)知,设,,.
在中,.
. ( http: / / www. / )
(3)n
评注 1在证明相似时同角的余角相等可以提供一种思路
2在做线段比例问题时不妨试着设出具体量,以便思考(但最终需还原为线段比例)
3 母子相似中蕴含的直角三角形与相似可以转化为三个相似的三角形
四 疑难点与易错点
直角三角形中的难点在于将其融入于多个图形中,转化为证明或解题中的一个重要环节。通过利用斜边中线,勾股定理,斜边与直角边,这些重难点,来证明全等相似或求出线段长度。还有特殊直角三角形三边与角的对应关系,从而找出角度或线段长度。直角三角形中的分类思想(以谁为斜边)
而直角三角形的易错点在于当在一个综合题中,勾股定理的平方有时会混淆为面积转化公式或相似比的转化公式。
五 真题演练
1. (2011四川广安,28,10分)某园艺公司对一块直角三角形的花圃进行改造.测得两直角边长为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.
2. (2011山东枣庄,15,4分)将一副三角尺如图所示叠放在一起,若=14cm,则阴影部分的面积是________cm2.
3. (2011江苏无锡,16,2分)如图,在Rt△ABC中,∠ACB = 90°,D、E、F分别是AB、BC、CA的中点,若CD = 5cm,
则EF = _________cm.
4. (2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .
5. (2011重庆綦江,16,4分) 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米. 当正方形DEFH运动到什么位置,即当AE= 米时,有DC=AE+BC.
答案
1:由题意可得,花圃的周长=8+8+=16+
2:
3: 5
4: 6cm2
5:
第二部分
1.(2010年四川省眉山市)下列命题中,真命题是
A.对角线互相垂直且相等的四边形是正方形
B.等腰梯形既是轴对称图形又是中心对称图形
C.圆的切线垂直于经过切点的半径
D.垂直于同一直线的两条直线互相垂直
2.(2010年四川省眉山市)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为
A.90° B.60° C.45° D.30°
3.(2010年辽宁省丹东市)图①是一个边长为的正方形,小颖将
图①中的阴影部分拼成图②的形状,由图①和图②
能验证的式子是( )
A.
B.
C.
D.
4.(2010浙江省喜嘉兴市)如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连结AE交CD于点M,连结BD交CE于点N,给出以下三个结论:①MN∥AB;②=+;③MN≤AB,其中正确结论的个数是( )
A.0 B.1 C.2 D.3
5、 (2010福建泉州市惠安县)矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为_____________.
6、(2010福建泉州市惠安县)如图,长方体的底面边长分别为1cm 和3cm,高为6cm.
①如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,
那么所用细线最短需要__________cm;
②如果从点A开始经过4个侧面缠绕3圈到达点B,
那么所用细线最短需要__________cm.
7、(2010年燕山)如图,在梯形ABCD中,AD∥BC,AB⊥AC,
∠B=45°, AD=1,BC=4,求DC的长.
8、(2010年宁德市)(本题满分13分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为时,求正方形的边长.
9、(2010年广东省广州市)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线=-+交折线OAB于点E.
(1)记△ODE的面积为S,求S与的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
10.(2010年山东省济南市)我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=600,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过450时,可确保山体不滑坡,改造时保持坡脚A 不动,从坡顶B 沿BC削进到E 处,问BE至少是多少米(结果保留根号)?
答案
1 C
2 C
3 B
4 D
5 5.5
6① 10, ②
7如图1,分别过点A、D作AE⊥BC于点E ,
DF⊥BC于点F. ………………………………1分
∴ AE // DF.又 AD // BC,
∴ 四边形AEFD是矩形.
∴ EF=AD=1. ……………………………………2分
∵ AB⊥AC,∠B=45°,BC= 4,
∴ AB=AC.
∴ AE=EC== 2. ……………………………3分
∴ DF=AE= 2,
CF=EC-EF= 1. ……………………………4分
在Rt△DFC中,∠DFC=90°,
∴DC=. …………………………5分
8解:⑴∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠BMA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
⑵①当M点落在BD的中点时,AM+CM的值最小.
②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小. ………………9分
理由如下:连接MN.由⑴知,△AMB≌△ENB,
∴AM=EN.
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
⑶过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=90°-60°=30°.
设正方形的边长为x,则BF=x,EF=.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴()2+(x+x)2=.
解得,x=(舍去负值).
∴正方形的边长为.
9(1)由题意得B(3,1).
若直线经过点A(3,0)时,则b=
若直线经过点B(3,1)时,则b=
若直线经过点C(0,1)时,则b=1
若直线与折线OAB的交点在OA上时,即1<b≤,如图25-a,
此时E(2b,0)
∴S=OE·CO=×2b×1=b
②若直线与折线OAB的交点在BA上时,即<b<,如图2
此时E(3,),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE +S△DBE )
= 3-[(2b-1)×1+×(5-2b)·( HYPERLINK "http://" )+×3()]=
∴
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。
由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,
由题易知,tan∠DEN=,DH=1,∴HE=2,
设菱形DNEM 的边长为a,
则在Rt△DHM中,由勾股定理知:,∴
∴S四边形DNEM=NE·DH=
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为.
10解:作BG⊥AD于G,作EF⊥AD于F,………………1’
∵Rt△ABG中,∠BAD=600,AB=40,
∴ BG =AB·sin600=20,AG = AB·cos600=20……………….3’
同理在Rt△AEF中,∠EAD=450,
∴AF=EF=BG=20,……………….3’
∴BE=FG=AF-AG=20()米. ……………….1’
B
B
A
A
C
O
E
D
D
E
C
O
F
图1
图2
F
A
C
B
E
F
D
(第16题)
第16题图
图①
图②
第4题图
(第10题)
A
B
C
D
E
G
第16题图
F
B
A
6cm
3cm
1cm
第6题图
B C
A D
E
A D
B C
N
M
C
D
B
A
E
O
D
A
B
C
E
图1
F
E
A D
B C
N
M
图2
图3
西安市西光中学 贾文 陈伟伦
第一部分
一 讲解
1 了解认识直角三角形的概念(基本特征,直角等)
2 理解掌握直角三角形的判断与其性质(勾股定理,斜边与直角边关系等)
3 灵活运用勾股定理解决简单问题
4 体验勾股定理的探索过程
5探索直角三角形的判断与其性质(尝试自己推导有关直角三角形的性质)
二 知识点
知识点一 直角三角形的基本性质
1直角三角形的两个锐角互余
可表示如下:∠C=90°∠A+∠B=90°
2在直角三角形中,30°角所对的直角边等于斜边的一半。
∠A=30°
可表示如下: BC=AB
∠C=90°
3、直角三角形斜边上的中线等于斜边的一半
∠ACB=90°
可表示如下: CD=AB=BD=AD
D为AB的中点
4、勾股定理
直角三角形两直角边a,b的平方和等于斜边c的平方,即
5、母子相似定理(射影定理)
在直角三角形中,斜边上的高线是两直角边在斜边上的摄影的比例中项,每条直角边是它们在斜边上的摄影和斜边的比例中项
∠ACB=90°
CD⊥AB
6、常用关系式
由三角形面积公式可得:
ABCD=ACBC
知识点二 直角三角形的判定
1、有一个角是直角的三角形是直角三角形。
2、如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、勾股定理的逆定理
如果三角形的三边长a,b,c有关系,那么这个三角形是直角三角形。
知识点三 锐角三角函数的概念
1、如图,在△ABC中,∠C=90°
①锐角A的对边与斜边的比叫做∠A的正弦,记为sinA,即
②锐角A的邻边与斜边的比叫做∠A的余弦,记为cosA,即
③锐角A的对边与邻边的比叫做∠A的正切,记为tanA,即
④锐角A的邻边与对边的比叫做∠A的余切,记为cotA,即
2、锐角三角函数的概念
锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数
3、一些特殊角的三角函数值
三角函数 0° 30° 45° 60° 90°
sinα 0 1
cosα 1 0
tanα 0 1 不存在
cotα 不存在 1 0
4、各锐角三角函数之间的关系
(1)互余关系
sinA=cos(90°—A),cosA=sin(90°—A)
tanA=cot(90°—A),cotA=tan(90°—A)
(2)平方关系
(3)倒数关系
tanAtan(90°—A)=1
(4)弦切关系
tanA=
知识点四 勾股定理中的方程思想
1.水中草问题
水深EB ,芦苇CB高出水一尺,被风吹倒后芦苇恰好浮在水面,请问水深多少?
解 设:水深x尺 在Rt△BED用勾股定理列出一个方程,求出水深.
2.矩形折叠
已知,在矩形FGJK中,FG=10 FK=8,将△FGH沿FH折叠,G落在KJ边上,记为点I,.求HJ长 .
解 设HJ长x先在Rt△FKI中求出KI,再求出IJ,再在Rt△HJI中用勾股定理求出HJ.
知识点五 勾股定理中的分类思想
1.Rt△ABC的两边分别为3cm和5cm,求以第三边为边长的正方形的面积
解①当以5cm为斜边时:
②当以未知边为斜边:
已知在△ABC中,AD为BC边上的高AB=15cm, AC=13cm ,AD=12cm ,求.
解①当△ABC为锐角三角形时,分别在Rt△ABD、Rt ADC中分别算出BD、DC ,再求出=84
②当△ABC为钝角三角形时,分别在Rt△ABD、Rt ACD中算出BD、CD, 再求出=24
知识点六 三维空间中的勾股定理
1 蚂蚁怎样走最近,如图蚂蚁在长方体A处,请问怎样走到达C’处最近? 请设计方案.
解: 三维空间中的勾股定理主要是在化归为二维空间,就是将A,C’两点放在同一个平面内,用勾股定理求出距离
解:设长方体长、宽、高分别为x、y、z,依题意,得:
①=
②=
③=
∵ 2xy>2xz>2yz
∴ ③<②<①
即走第三条路径最短。
2.在长宽高为a,b,c的电梯内放置一竿子的最长长度为
AC’=
知识点七 勾股定理的证明(等积法)
∵
∴
即,
三 考点精讲
例题一
如图所示,在△ABC中,角ACB为90,点O是△ABC内一点,且S△OAB=S△OBC=S△OCA,那么,OA +OB 与OC 的比值是多少
考点一 直角三角形三边关系(勾股定理)
分析 此题主要关于直角三角形面积与三边关系,所以辅助线应该做有关OA OB的垂线段。并且将垂线段与OC联系起来。
解 过点O分别作OM ON垂直于AC CB
OM ON 的平方和=OC的平方
ON=三分之一的AC OM=三分之一的CB
NB=2MO AM=2ON
OA +OB :OC =5:1
评注 1三角形勾股定理之间的转换,即某一边等于某一边就有其平方等于另一边的平方
2直角三角形面积比转换为边长或高的比
3从需证明结论出发,找到面积比与勾股定理之间的转化关系
例题二
(2009湖北武汉)如图1,在中,,于点,点是边上一点,连接交于,交边于点.
(1)求证:;
(2)当为边中点,时,如图2,求的值;
(3)当为边中点,时,请直接写出的值.
考点2 直角三角形两锐角互余
分析 此题中包含多个直角三角形,首先应梳理清楚关系。另外其中包含形似三角形对应线段成比例的问题,应通过成比例线段或直角三角形中的同角的余角相等,来推导出结论。
解 (1)∠ECO=∠BAF(摄影定理) ∠EOC=∠ABF(角BOA的两余角相等) 所以△ABF∽△COE
(2)于,
..
设,则,
.
,
.
由(1)知,设,,.
在中,.
. ( http: / / www. / )
(3)n
评注 1在证明相似时同角的余角相等可以提供一种思路
2在做线段比例问题时不妨试着设出具体量,以便思考(但最终需还原为线段比例)
3 母子相似中蕴含的直角三角形与相似可以转化为三个相似的三角形
四 疑难点与易错点
直角三角形中的难点在于将其融入于多个图形中,转化为证明或解题中的一个重要环节。通过利用斜边中线,勾股定理,斜边与直角边,这些重难点,来证明全等相似或求出线段长度。还有特殊直角三角形三边与角的对应关系,从而找出角度或线段长度。直角三角形中的分类思想(以谁为斜边)
而直角三角形的易错点在于当在一个综合题中,勾股定理的平方有时会混淆为面积转化公式或相似比的转化公式。
五 真题演练
1. (2011四川广安,28,10分)某园艺公司对一块直角三角形的花圃进行改造.测得两直角边长为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.
2. (2011山东枣庄,15,4分)将一副三角尺如图所示叠放在一起,若=14cm,则阴影部分的面积是________cm2.
3. (2011江苏无锡,16,2分)如图,在Rt△ABC中,∠ACB = 90°,D、E、F分别是AB、BC、CA的中点,若CD = 5cm,
则EF = _________cm.
4. (2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .
5. (2011重庆綦江,16,4分) 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米. 当正方形DEFH运动到什么位置,即当AE= 米时,有DC=AE+BC.
答案
1:由题意可得,花圃的周长=8+8+=16+
2:
3: 5
4: 6cm2
5:
第二部分
1.(2010年四川省眉山市)下列命题中,真命题是
A.对角线互相垂直且相等的四边形是正方形
B.等腰梯形既是轴对称图形又是中心对称图形
C.圆的切线垂直于经过切点的半径
D.垂直于同一直线的两条直线互相垂直
2.(2010年四川省眉山市)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为
A.90° B.60° C.45° D.30°
3.(2010年辽宁省丹东市)图①是一个边长为的正方形,小颖将
图①中的阴影部分拼成图②的形状,由图①和图②
能验证的式子是( )
A.
B.
C.
D.
4.(2010浙江省喜嘉兴市)如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连结AE交CD于点M,连结BD交CE于点N,给出以下三个结论:①MN∥AB;②=+;③MN≤AB,其中正确结论的个数是( )
A.0 B.1 C.2 D.3
5、 (2010福建泉州市惠安县)矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为_____________.
6、(2010福建泉州市惠安县)如图,长方体的底面边长分别为1cm 和3cm,高为6cm.
①如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,
那么所用细线最短需要__________cm;
②如果从点A开始经过4个侧面缠绕3圈到达点B,
那么所用细线最短需要__________cm.
7、(2010年燕山)如图,在梯形ABCD中,AD∥BC,AB⊥AC,
∠B=45°, AD=1,BC=4,求DC的长.
8、(2010年宁德市)(本题满分13分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为时,求正方形的边长.
9、(2010年广东省广州市)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线=-+交折线OAB于点E.
(1)记△ODE的面积为S,求S与的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.
10.(2010年山东省济南市)我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=600,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过450时,可确保山体不滑坡,改造时保持坡脚A 不动,从坡顶B 沿BC削进到E 处,问BE至少是多少米(结果保留根号)?
答案
1 C
2 C
3 B
4 D
5 5.5
6① 10, ②
7如图1,分别过点A、D作AE⊥BC于点E ,
DF⊥BC于点F. ………………………………1分
∴ AE // DF.又 AD // BC,
∴ 四边形AEFD是矩形.
∴ EF=AD=1. ……………………………………2分
∵ AB⊥AC,∠B=45°,BC= 4,
∴ AB=AC.
∴ AE=EC== 2. ……………………………3分
∴ DF=AE= 2,
CF=EC-EF= 1. ……………………………4分
在Rt△DFC中,∠DFC=90°,
∴DC=. …………………………5分
8解:⑴∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠BMA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
⑵①当M点落在BD的中点时,AM+CM的值最小.
②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小. ………………9分
理由如下:连接MN.由⑴知,△AMB≌△ENB,
∴AM=EN.
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
⑶过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=90°-60°=30°.
设正方形的边长为x,则BF=x,EF=.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴()2+(x+x)2=.
解得,x=(舍去负值).
∴正方形的边长为.
9(1)由题意得B(3,1).
若直线经过点A(3,0)时,则b=
若直线经过点B(3,1)时,则b=
若直线经过点C(0,1)时,则b=1
若直线与折线OAB的交点在OA上时,即1<b≤,如图25-a,
此时E(2b,0)
∴S=OE·CO=×2b×1=b
②若直线与折线OAB的交点在BA上时,即<b<,如图2
此时E(3,),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE +S△DBE )
= 3-[(2b-1)×1+×(5-2b)·( HYPERLINK "http://" )+×3()]=
∴
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。
由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,
由题易知,tan∠DEN=,DH=1,∴HE=2,
设菱形DNEM 的边长为a,
则在Rt△DHM中,由勾股定理知:,∴
∴S四边形DNEM=NE·DH=
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为.
10解:作BG⊥AD于G,作EF⊥AD于F,………………1’
∵Rt△ABG中,∠BAD=600,AB=40,
∴ BG =AB·sin600=20,AG = AB·cos600=20……………….3’
同理在Rt△AEF中,∠EAD=450,
∴AF=EF=BG=20,……………….3’
∴BE=FG=AF-AG=20()米. ……………….1’
B
B
A
A
C
O
E
D
D
E
C
O
F
图1
图2
F
A
C
B
E
F
D
(第16题)
第16题图
图①
图②
第4题图
(第10题)
A
B
C
D
E
G
第16题图
F
B
A
6cm
3cm
1cm
第6题图
B C
A D
E
A D
B C
N
M
C
D
B
A
E
O
D
A
B
C
E
图1
F
E
A D
B C
N
M
图2
图3
同课章节目录
