34、二次函数y=ax2+bx+c的图像
文档属性
| 名称 | 34、二次函数y=ax2+bx+c的图像 |

|
|
| 格式 | zip | ||
| 文件大小 | 91.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-03 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
二次函数y=ax2+bx+c的图像
知识梳理
1、抛物线y=ax2的顶点是 ,对称轴为 ,当a>0时开口向 ,当a<0时开口向 .
原点
y轴
上
下
2、抛物线y=a(x-h)2+k有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
x=h
(3)顶点坐标是( ).
h,k
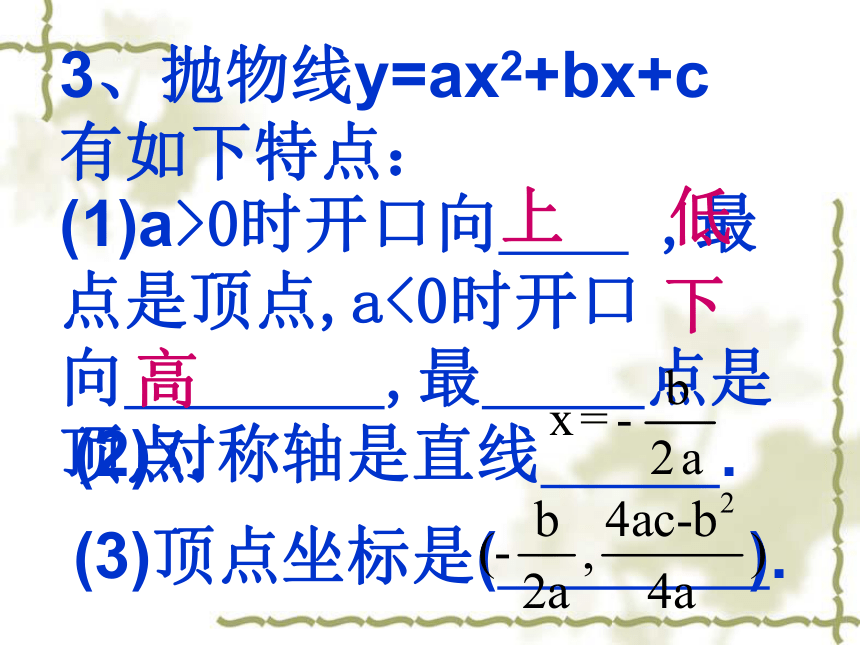
3、抛物线y=ax2+bx+c有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
(3)顶点坐标是( ).
怎样确定二次函数的解析式
二次函数的解析式的三种形式:
1.一般式: ,
2.顶点式: ,
3.乘积式: .
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
由于二次函数有三个待定系数a,b,c,所以求二次函数的解析式一般需三个条件.确定二次函数解析式的常用方法有:
1.如果已知图象上的任意三点,可用一般式y=ax2+bx+c;
2.如果已知顶点坐标或对称轴方程等,可用顶点式y=a(x-h)2+k;
3.如果已知二次函数的图象与x轴的两个交点坐标(x1,0)和(x2,0),可用乘积式y=a(x-x1)(x-x2)
二次函数与一元二次方程有什么关系
抛物线y=ax2+bx+c(a≠0)与x轴交点的横坐标,就是方程ax2+bx+c=0(a≠0)的根,反之亦然.
1.Δ=b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有两个交点;
2.Δ=b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴只有一个交点,即顶点在x轴上;
3.Δ=b2-4ac<0时,方程没有实数根,抛物线与x轴没有交点;
例1.已知二次函数的图像顶点是(1,-3),且经过(2,0)求这个函数的解析式.(你能用几种方法?)
法一:设所求的二次函数为y=ax2+bx+c,由已知得
解得
a=3 b=-6 c=0
所求解析式为
y=3x2-6x
法二:设所求的二次函数为y=a(x-h)2+k,由已知得
h=1 k=-3 0=a(2-h)2+k
解得
a=3 h=1 k=-3
所求解析式为
y=3(x-1)2-3
法三:设所求的二次函数为 y=a(x-x1)(x-x2),其中x1 ,x2为抛物线与x轴交点的横坐标.
由题意知抛物线与x轴的两个交点为(2,0),(0,0), 得
y=a(x-2)x
把(1,-3)代入得
a=3,y=3(x-2)x
同步训练
1.抛物线y=ax2+bx+c的顶点坐标是 ,对称轴是 ,当 时,开口向下,当 时,有最低点. 2.抛物线y=3x2-4x+1的顶点坐标是 ,对称轴是 ,与x轴的交点是 ,与y轴的交点是 。
a<0
a>0
(0,1)
最新考题
某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用长为40m的栅 栏围成.设BC长 为x,面积为y.
1.求y与x之间的函数关系式,并求自变量取值范围. 2.满足条件的花园面积能达到200m2吗 3.描述图像的变化趋势,并判断当x取何值时,花园面积最大 最大面积为多少
家庭作业
1.抛物线y=2x2+bx+c的顶点坐标为(1,-2),求b,c. 2.抛物线y=x2-2(k+1)x+16的顶点在y轴上,求k的值. 3.把函数y=x2-x+1写成顶点式为 ,其顶点坐标为 ,对称轴为 .
二次函数y=ax2+bx+c的图像
知识梳理
1、抛物线y=ax2的顶点是 ,对称轴为 ,当a>0时开口向 ,当a<0时开口向 .
原点
y轴
上
下
2、抛物线y=a(x-h)2+k有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
x=h
(3)顶点坐标是( ).
h,k
3、抛物线y=ax2+bx+c有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
(3)顶点坐标是( ).
怎样确定二次函数的解析式
二次函数的解析式的三种形式:
1.一般式: ,
2.顶点式: ,
3.乘积式: .
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
由于二次函数有三个待定系数a,b,c,所以求二次函数的解析式一般需三个条件.确定二次函数解析式的常用方法有:
1.如果已知图象上的任意三点,可用一般式y=ax2+bx+c;
2.如果已知顶点坐标或对称轴方程等,可用顶点式y=a(x-h)2+k;
3.如果已知二次函数的图象与x轴的两个交点坐标(x1,0)和(x2,0),可用乘积式y=a(x-x1)(x-x2)
二次函数与一元二次方程有什么关系
抛物线y=ax2+bx+c(a≠0)与x轴交点的横坐标,就是方程ax2+bx+c=0(a≠0)的根,反之亦然.
1.Δ=b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有两个交点;
2.Δ=b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴只有一个交点,即顶点在x轴上;
3.Δ=b2-4ac<0时,方程没有实数根,抛物线与x轴没有交点;
例1.已知二次函数的图像顶点是(1,-3),且经过(2,0)求这个函数的解析式.(你能用几种方法?)
法一:设所求的二次函数为y=ax2+bx+c,由已知得
解得
a=3 b=-6 c=0
所求解析式为
y=3x2-6x
法二:设所求的二次函数为y=a(x-h)2+k,由已知得
h=1 k=-3 0=a(2-h)2+k
解得
a=3 h=1 k=-3
所求解析式为
y=3(x-1)2-3
法三:设所求的二次函数为 y=a(x-x1)(x-x2),其中x1 ,x2为抛物线与x轴交点的横坐标.
由题意知抛物线与x轴的两个交点为(2,0),(0,0), 得
y=a(x-2)x
把(1,-3)代入得
a=3,y=3(x-2)x
同步训练
1.抛物线y=ax2+bx+c的顶点坐标是 ,对称轴是 ,当 时,开口向下,当 时,有最低点. 2.抛物线y=3x2-4x+1的顶点坐标是 ,对称轴是 ,与x轴的交点是 ,与y轴的交点是 。
a<0
a>0
(0,1)
最新考题
某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用长为40m的栅 栏围成.设BC长 为x,面积为y.
1.求y与x之间的函数关系式,并求自变量取值范围. 2.满足条件的花园面积能达到200m2吗 3.描述图像的变化趋势,并判断当x取何值时,花园面积最大 最大面积为多少
家庭作业
1.抛物线y=2x2+bx+c的顶点坐标为(1,-2),求b,c. 2.抛物线y=x2-2(k+1)x+16的顶点在y轴上,求k的值. 3.把函数y=x2-x+1写成顶点式为 ,其顶点坐标为 ,对称轴为 .
