35、二次函数y=ax2+bx+c的图像2
文档属性
| 名称 | 35、二次函数y=ax2+bx+c的图像2 |  | |
| 格式 | zip | ||
| 文件大小 | 105.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-03 20:58:05 | ||
图片预览








文档简介
(共30张PPT)
二次函数y=ax2+bx+c的图像
知识梳理
1、抛物线y=ax2的顶点是 ,对称轴为 ,当a>0时开口向 ,当a<0时开口向 .
原点
y轴
上
下
2、抛物线y=a(x-h)2+k有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
x=h
(3)顶点坐标是( ).
h,k
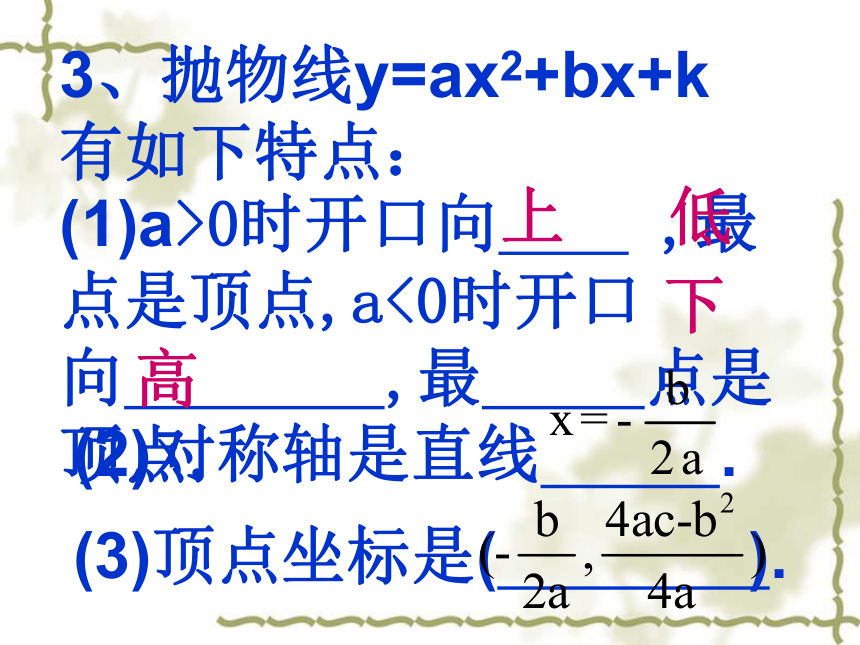
3、抛物线y=ax2+bx+k有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
(3)顶点坐标是( ).
怎样确定二次函数的解析式
二次函数的解析式的三种形式:
1.一般式: ,
2.顶点式: ,
3.乘积式: .
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
由于二次函数有三个待定系数a,b,c,所以求二次函数的解析式一般需三个条件.确定二次函数解析式的常用方法有:
1.如果已知图象上的任意三点,可用一般式y=ax2+bx+c;
2.如果已知顶点坐标或对称轴方程等,可用顶点式y=a(x-h)2+k;
3.如果已知二次函数的图象与x轴的两个交点坐标(x1,0)和(x2,0),可用乘积式y=a(x-x1)(x-x2)
二次函数与一元二次方程有什么关系
抛物线y=ax2+bx+c(a≠0)与x轴交点的横坐标,就是方程ax2+bx+c=0(a≠0)的根,反之亦然.
1.Δ=b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有两个交点;
2.Δ=b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴只有一个交点,即顶点在x轴上;
3.Δ=b2-4ac<0时,方程没有实数根,抛物线与x轴没有交点;
例1.写出函数y=-3x2+2x+5的顶点式和乘积式,并说出图像的开口方向、对称轴和顶点坐标。
令-3x2+2x+5=0,解这个方程得:x1=-1,x2=5/3
所以所求函数的乘积式为:
y=-3(x+1)(x-5/3)
例2.如图抛物线y=ax2+bx+c 的对称轴是x=1, 则下列关系成立 的是( ) A.abc>0 B.a+b+c<0 C.a2>ab-ac
C
经验总结
这是一典型的数形结合问题
1.由开口方向决定a的符号;
2.抛物线与y轴交于(0,c),所以由与y轴交点的纵坐标决定c的符号;
4.由x=1时函数值的符号决定a+b+c的符号;
5.由x=-1时函数值的符号决定a-b+c的符号.
把y=0代入原函数得
把x=0代入原函数得y=1 所以 B(0,1)
解方程得
经验总结
1、求抛物线的顶点坐标有两种方法,即配方法和公式法。
2、求抛物线与坐标轴的交点问题,是考试的热点难点,一定要掌握其计算方法。
家庭作业
1.已知一个二次函数的图象经过(2,5).(-2,-3).(1,0)三点,求函数解析式. 2.y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标是-1、3,与y轴交点的纵坐标是 ,求解析式。
二次函数y=ax2+bx+c的图像
知识梳理
1、抛物线y=ax2的顶点是 ,对称轴为 ,当a>0时开口向 ,当a<0时开口向 .
原点
y轴
上
下
2、抛物线y=a(x-h)2+k有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
x=h
(3)顶点坐标是( ).
h,k
3、抛物线y=ax2+bx+k有如下特点:
(1)a>0时开口向 ,最 点是顶点,a<0时开口向 ,最 点是顶点.
上
低
下
高
(2)对称轴是直线 .
(3)顶点坐标是( ).
怎样确定二次函数的解析式
二次函数的解析式的三种形式:
1.一般式: ,
2.顶点式: ,
3.乘积式: .
y=ax2+bx+c
y=a(x-h)2+k
y=a(x-x1)(x-x2)
由于二次函数有三个待定系数a,b,c,所以求二次函数的解析式一般需三个条件.确定二次函数解析式的常用方法有:
1.如果已知图象上的任意三点,可用一般式y=ax2+bx+c;
2.如果已知顶点坐标或对称轴方程等,可用顶点式y=a(x-h)2+k;
3.如果已知二次函数的图象与x轴的两个交点坐标(x1,0)和(x2,0),可用乘积式y=a(x-x1)(x-x2)
二次函数与一元二次方程有什么关系
抛物线y=ax2+bx+c(a≠0)与x轴交点的横坐标,就是方程ax2+bx+c=0(a≠0)的根,反之亦然.
1.Δ=b2-4ac>0时,方程有两个不相等的实数根,抛物线与x轴有两个交点;
2.Δ=b2-4ac=0时,方程有两个相等的实数根,抛物线与x轴只有一个交点,即顶点在x轴上;
3.Δ=b2-4ac<0时,方程没有实数根,抛物线与x轴没有交点;
例1.写出函数y=-3x2+2x+5的顶点式和乘积式,并说出图像的开口方向、对称轴和顶点坐标。
令-3x2+2x+5=0,解这个方程得:x1=-1,x2=5/3
所以所求函数的乘积式为:
y=-3(x+1)(x-5/3)
例2.如图抛物线y=ax2+bx+c 的对称轴是x=1, 则下列关系成立 的是( ) A.abc>0 B.a+b+c<0 C.a2>ab-ac
C
经验总结
这是一典型的数形结合问题
1.由开口方向决定a的符号;
2.抛物线与y轴交于(0,c),所以由与y轴交点的纵坐标决定c的符号;
4.由x=1时函数值的符号决定a+b+c的符号;
5.由x=-1时函数值的符号决定a-b+c的符号.
把y=0代入原函数得
把x=0代入原函数得y=1 所以 B(0,1)
解方程得
经验总结
1、求抛物线的顶点坐标有两种方法,即配方法和公式法。
2、求抛物线与坐标轴的交点问题,是考试的热点难点,一定要掌握其计算方法。
家庭作业
1.已知一个二次函数的图象经过(2,5).(-2,-3).(1,0)三点,求函数解析式. 2.y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标是-1、3,与y轴交点的纵坐标是 ,求解析式。
