2020-2021学年北师大 版 七年级数学下册第四章全等三角形的判定方法复习课件(20张)
文档属性
| 名称 | 2020-2021学年北师大 版 七年级数学下册第四章全等三角形的判定方法复习课件(20张) |  | |
| 格式 | ppt | ||
| 文件大小 | 771.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 15:44:57 | ||
图片预览




文档简介
(共20张PPT)
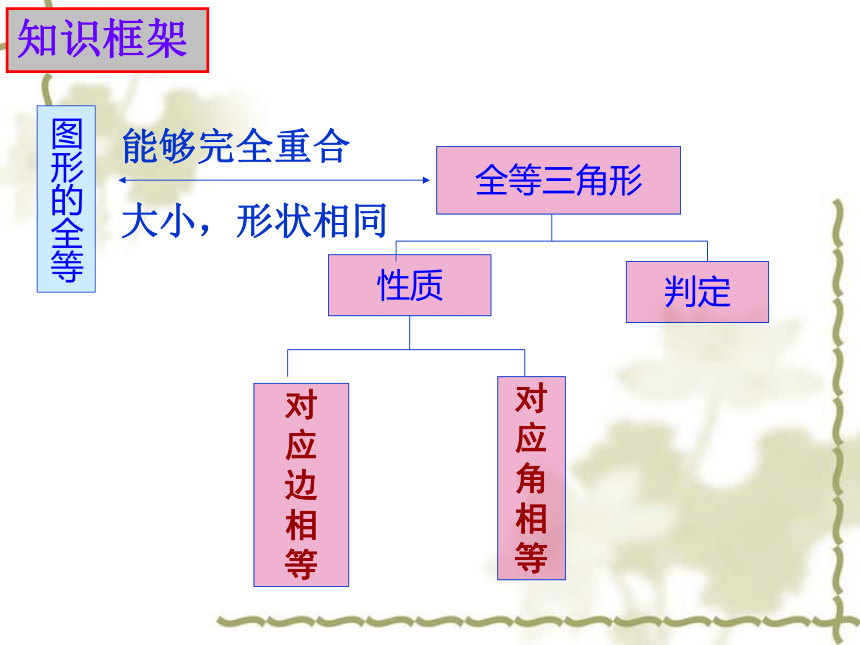
全等三角形
性质
判定
对
应
边
相
等
对
应
角
相
等
能够完全重合
大小,形状相同
知识框架
图形的全等
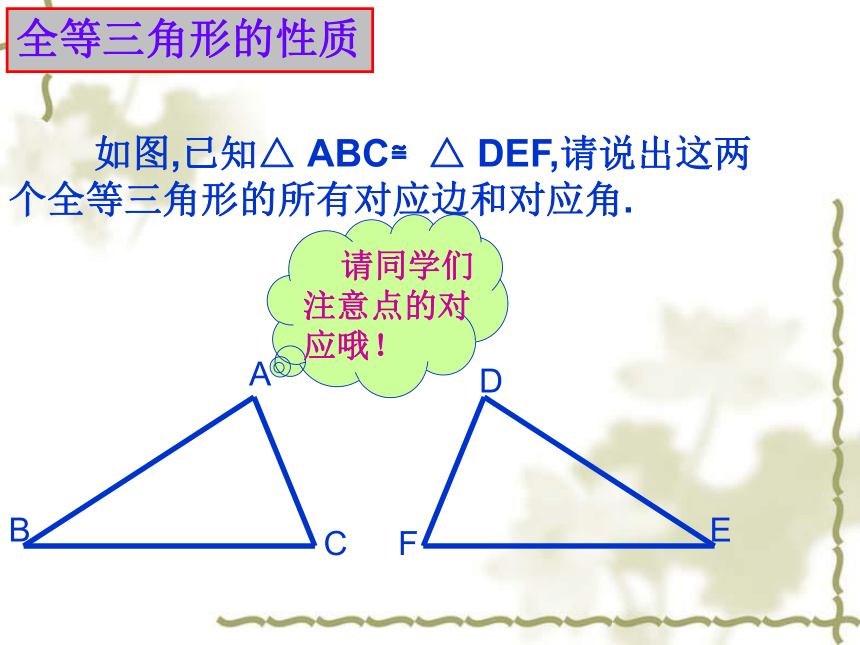
C
A
B
如图,已知△
ABC≌△
DEF,请说出这两个全等三角形的所有对应边和对应角.
E
D
F
全等三角形的性质
请同学们注意点的对应哦!
1、判断两个三角形全等的方法:
判定方法
条
件
边边边
(SSS)
三边对应相等
边角边
(SAS)
两边和他们的 对应相等
角边角
(ASA)
两角和他们的夹边对应相等
角角边
(AAS)
两角和 对应相等
夹角
其中一角的对边
三角形全等的判定方法
2、判断两个直角三角形全等的方法:
a.一般三角形全等的判定方法对直角三角形全等
的判定同样适用.
b.
判定方法
条
件
斜边直角边
(HL)
斜边和一条直角边对应相等
直角三角形全等的判定方法
历年中考对三角形全等的判定及性质的考查都很简单,主要分三种类型;本节课我们主要复习第一
种题型。
题型一:“添加条件”型
题型二:“线段和差,角的和差”型
题型三:”平行性质“型
中考链接
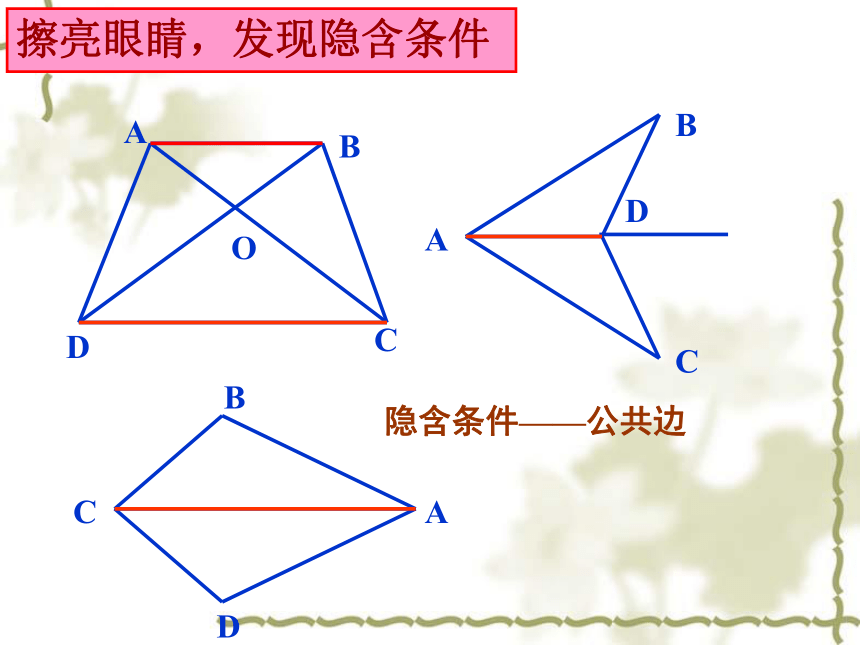
擦亮眼睛,发现隐含条件
A
D
C
B
A
D
C
B
D
B
C
A
O
隐含条件——公共边
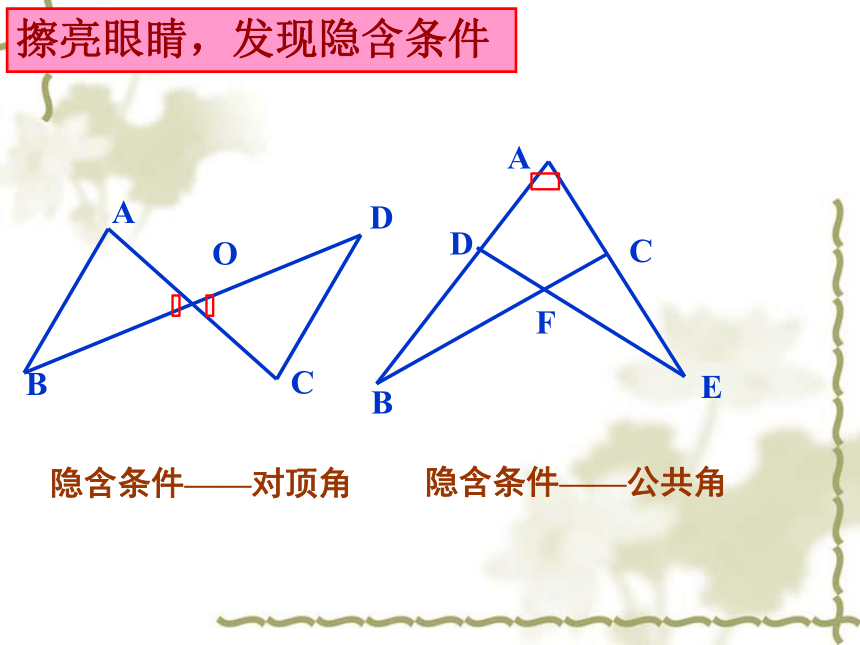
A
O
C
D
B
C
B
A
F
E
D
隐含条件——公共角
隐含条件——对顶角
擦亮眼睛,发现隐含条件
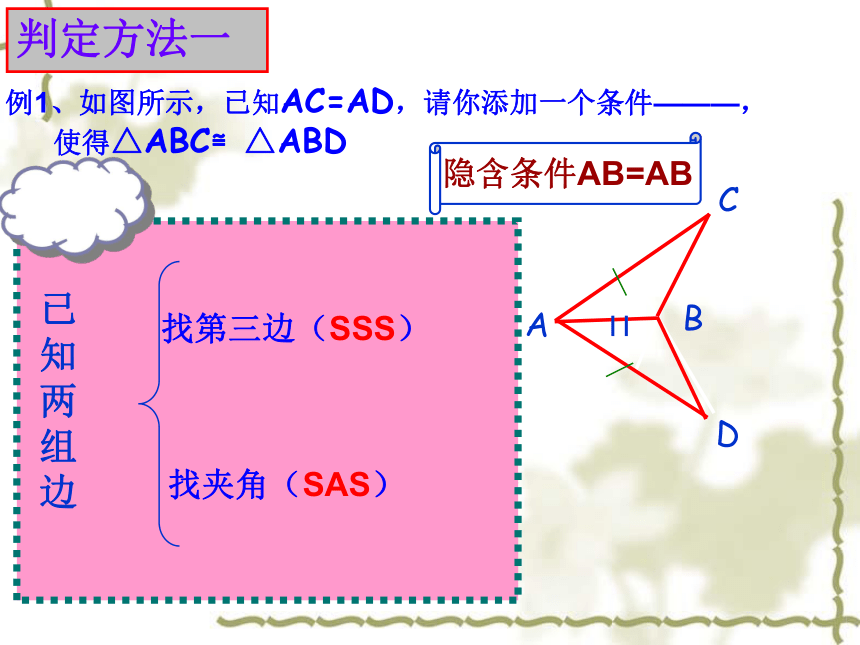
例1、如图所示,已知AC=AD,请你添加一个条件———,
使得△ABC≌△ABD
B
A
C
D
隐含条件AB=AB
判定方法一
已知两组边
找第三边(SSS)
找夹角(SAS)
如图,已知AD=AC,要使
△ADB≌△ACB,需要添加的一个
条件是__________
__________
______。
请说明理由。
BD=BC
或者∠DAB=∠CAB
判定方法一—练习题
B
C
D
A
变式1:如图,已知∠CAB=∠DAB,请你添加一个条件————,使得
△ABC≌△ABD
B
A
C
D
已知一边一角
这边为角的邻边
找夹角的另一边(SAS)
找夹边的另一角(ASA)
找找边的对角(AAS)
隐含条件AB=AB
判定方法二
3.如图,已知AB=AE,要使△ABC≌△AED,需要添
加的一个条件是
______________________________。
请说明理由.
AC=AD
,∠B=∠E
或
∠ACB=∠ADE
判定方法二--练习题
A
B
C
D
E
变式2:如图,已知∠C=∠D,请你添加一个条件————,
使得△ABC≌△ABD
B
A
C
D
已知一边一角
这边为角的对边
找任一角(AAS)
隐含条件AB=AB
判定方法三
添加AC=AD或者AB=AE可以吗?
要防止出现“SSA”的错误!
4.如图,已知BC=ED,要使△ABC≌△AED,需要添
加的一个条件是________________________。
并求证:
AB=AE
∠B=∠E
或者∠ACB=∠ADE
判定方法三—练习题
A
B
C
D
E
A
D
E
C
B
变式3、如图所示:已知∠B=∠C,请你添加一个条件————,使得
△ABE≌△ACD
已知两角
找夹边(ASA)
找对边(AAS)
∠A为公共角
判定方法四
如图所示:已知∠B=∠D,请你添加一个条件
—————————,使得△ABO≌△CDO。
并求证∠A=∠C
判定方法四—练习题
A
O
C
D
B
添加的条件:
AB=CD,OA=OC或者OB=OC
③构定第三个条件
②找到题中已知条件和隐含的条件,选择判定方法。
①观察结论中的线段或角,先确定在哪两
个可能全等的三角形中。
1、全等是说明线段或角相等的重要方法之一。
说明时注意:
请同学们注意书写格式哦!
1.如图所示:已知
∠BAD=∠CDA
,
(1)请你添加一个条件,
△ABD≌△DCA
(2)求证:BD=AC
(3)求证:△AED是等腰三角形.
课堂作业
我学会了-------
我弄懂了-------
还有------
课后作业
遨游了知识的海洋,老师发现你们是很棒的,做作业可要小心细致呦!
作业1:本土攻略优练本
能力训练综合能力测试11题。
全等三角形
性质
判定
对
应
边
相
等
对
应
角
相
等
能够完全重合
大小,形状相同
知识框架
图形的全等
C
A
B
如图,已知△
ABC≌△
DEF,请说出这两个全等三角形的所有对应边和对应角.
E
D
F
全等三角形的性质
请同学们注意点的对应哦!
1、判断两个三角形全等的方法:
判定方法
条
件
边边边
(SSS)
三边对应相等
边角边
(SAS)
两边和他们的 对应相等
角边角
(ASA)
两角和他们的夹边对应相等
角角边
(AAS)
两角和 对应相等
夹角
其中一角的对边
三角形全等的判定方法
2、判断两个直角三角形全等的方法:
a.一般三角形全等的判定方法对直角三角形全等
的判定同样适用.
b.
判定方法
条
件
斜边直角边
(HL)
斜边和一条直角边对应相等
直角三角形全等的判定方法
历年中考对三角形全等的判定及性质的考查都很简单,主要分三种类型;本节课我们主要复习第一
种题型。
题型一:“添加条件”型
题型二:“线段和差,角的和差”型
题型三:”平行性质“型
中考链接
擦亮眼睛,发现隐含条件
A
D
C
B
A
D
C
B
D
B
C
A
O
隐含条件——公共边
A
O
C
D
B
C
B
A
F
E
D
隐含条件——公共角
隐含条件——对顶角
擦亮眼睛,发现隐含条件
例1、如图所示,已知AC=AD,请你添加一个条件———,
使得△ABC≌△ABD
B
A
C
D
隐含条件AB=AB
判定方法一
已知两组边
找第三边(SSS)
找夹角(SAS)
如图,已知AD=AC,要使
△ADB≌△ACB,需要添加的一个
条件是__________
__________
______。
请说明理由。
BD=BC
或者∠DAB=∠CAB
判定方法一—练习题
B
C
D
A
变式1:如图,已知∠CAB=∠DAB,请你添加一个条件————,使得
△ABC≌△ABD
B
A
C
D
已知一边一角
这边为角的邻边
找夹角的另一边(SAS)
找夹边的另一角(ASA)
找找边的对角(AAS)
隐含条件AB=AB
判定方法二
3.如图,已知AB=AE,要使△ABC≌△AED,需要添
加的一个条件是
______________________________。
请说明理由.
AC=AD
,∠B=∠E
或
∠ACB=∠ADE
判定方法二--练习题
A
B
C
D
E
变式2:如图,已知∠C=∠D,请你添加一个条件————,
使得△ABC≌△ABD
B
A
C
D
已知一边一角
这边为角的对边
找任一角(AAS)
隐含条件AB=AB
判定方法三
添加AC=AD或者AB=AE可以吗?
要防止出现“SSA”的错误!
4.如图,已知BC=ED,要使△ABC≌△AED,需要添
加的一个条件是________________________。
并求证:
AB=AE
∠B=∠E
或者∠ACB=∠ADE
判定方法三—练习题
A
B
C
D
E
A
D
E
C
B
变式3、如图所示:已知∠B=∠C,请你添加一个条件————,使得
△ABE≌△ACD
已知两角
找夹边(ASA)
找对边(AAS)
∠A为公共角
判定方法四
如图所示:已知∠B=∠D,请你添加一个条件
—————————,使得△ABO≌△CDO。
并求证∠A=∠C
判定方法四—练习题
A
O
C
D
B
添加的条件:
AB=CD,OA=OC或者OB=OC
③构定第三个条件
②找到题中已知条件和隐含的条件,选择判定方法。
①观察结论中的线段或角,先确定在哪两
个可能全等的三角形中。
1、全等是说明线段或角相等的重要方法之一。
说明时注意:
请同学们注意书写格式哦!
1.如图所示:已知
∠BAD=∠CDA
,
(1)请你添加一个条件,
△ABD≌△DCA
(2)求证:BD=AC
(3)求证:△AED是等腰三角形.
课堂作业
我学会了-------
我弄懂了-------
还有------
课后作业
遨游了知识的海洋,老师发现你们是很棒的,做作业可要小心细致呦!
作业1:本土攻略优练本
能力训练综合能力测试11题。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
