第三章 圆周运动 单元测试(提高版)word版含答案
文档属性
| 名称 | 第三章 圆周运动 单元测试(提高版)word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-25 23:07:25 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
第三章
圆周运动单元测试(提高版)
一、单选题
1.为欢度春节,某酒店的旋转门上A,B两点粘贴着小型装饰物(视为质点)可绕中心轴转动,
到中心轴的距离为
到中心轴距离的两倍,
处装饰物的质量为
处装饰物质量的两倍,如图所示。当旋转门匀速转动时,下列说法正确的是(??
)
A.?A,B两处装饰物的周期之比为
B.?A,B两处装饰物的向心加速度大小之比为
C.?A,B两处装饰物的线速度大小之比为
D.?A,B两处装饰物受到的向心力大小之比为
2.有一种自行车,它有能向车头灯泡供电的小型发电机,其原理示意图如图甲所示:图中N、S是一对固定的磁极,磁极间有一固定在绝缘转轴上的矩形线圈,转轴的一端有一个与自行车后轮边缘接触的摩擦轮。如图乙所示,当车轮转动时,因摩擦而带动摩擦轮转动,从而使线圈在磁场中转动而产生电流给车头灯泡供电。关于此装置,下列说法正确的是(??
)
A.?自行车的速度加倍,线圈中交变电流的周期加倍
B.?自行车的速度加倍,线圈中交变电流的周期不变
C.?小灯泡的电功率与自行车的速度成正比
D.?小灯泡的电功率与自行车速度的平方成正比
3.某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3
,
若甲轮匀速转动角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的线速度大小为(??
)
A.?r1ω?????????????????????????????????????B.?r2ω?????????????????????????????????????C.?r3ω?????????????????????????????????????D.?
4.如图所示,地球可以看成一个巨大的拱形桥,桥面半径R=6400km,地面上行驶的汽车中驾驶员的重力G=800N,在汽车不离开地面的前提下,下列分析中正确的是(??
)
A.?汽车的速度越大,则汽车对地面的压力也越大
B.?不论汽车的行驶速度如何,驾驶员对座椅压力大小都等于800N
C.?只要汽车行驶,驾驶员对座椅压力大小都小于他自身的重力
D.?如果某时刻速度增大到使汽车对地面压力为零,则此时驾驶员会有超重的感觉
5.一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替.如图(a)所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径.现将一物体沿与水平面成α角的方向已速度υ0抛出,如图(b)所示.则在其轨迹最高点P处的曲率半径是(??
)
A.???????????????????????????????B.?
??????????????????????????????C.???????????????????????????????D.?
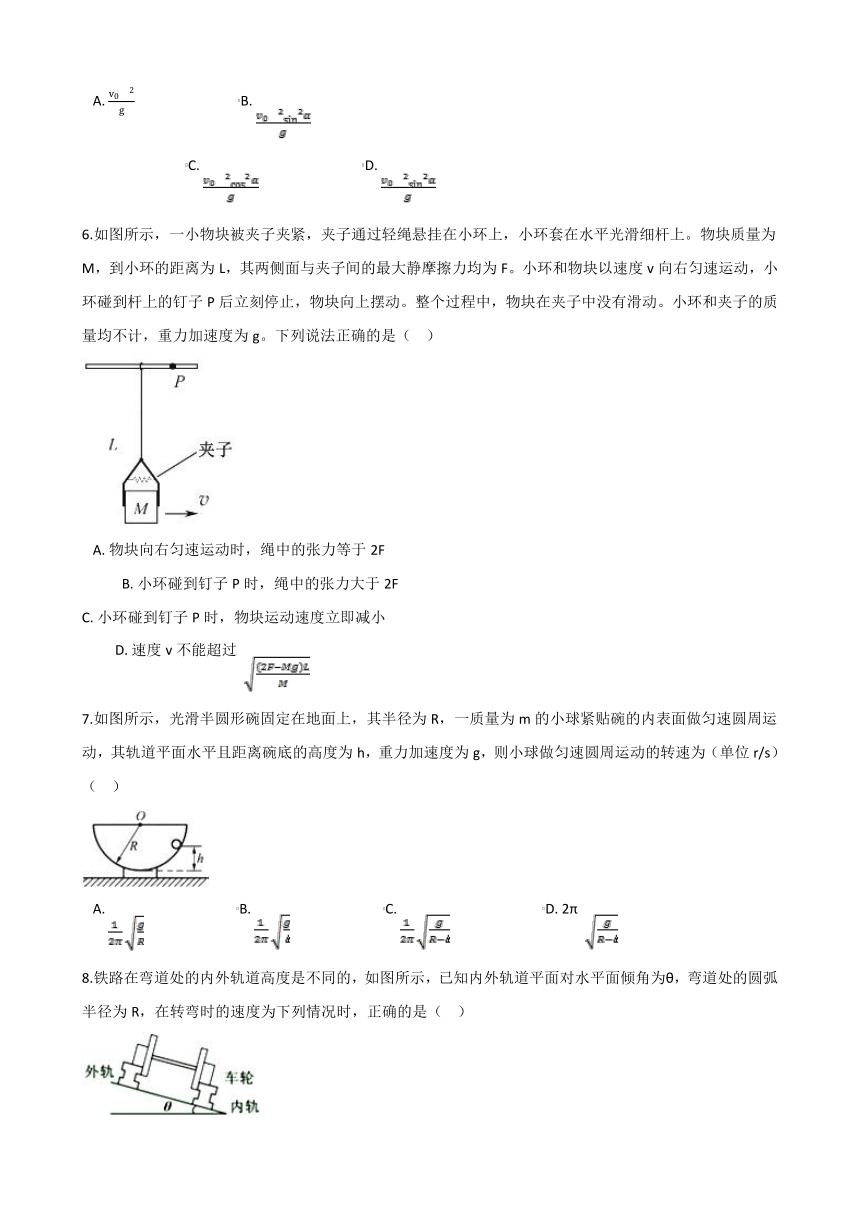
6.如图所示,一小物块被夹子夹紧,夹子通过轻绳悬挂在小环上,小环套在水平光滑细杆上。物块质量为M,到小环的距离为L,其两侧面与夹子间的最大静摩擦力均为F。小环和物块以速度v向右匀速运动,小环碰到杆上的钉子P后立刻停止,物块向上摆动。整个过程中,物块在夹子中没有滑动。小环和夹子的质量均不计,重力加速度为g。下列说法正确的是(??
)
A.?物块向右匀速运动时,绳中的张力等于2F
???????????B.?小环碰到钉子P时,绳中的张力大于2F
C.?小环碰到钉子P时,物块运动速度立即减小
?????????D.?速度v不能超过
7.如图所示,光滑半圆形碗固定在地面上,其半径为R,一质量为m的小球紧贴碗的内表面做匀速圆周运动,其轨道平面水平且距离碗底的高度为h,重力加速度为g,则小球做匀速圆周运动的转速为(单位r/s)(??
)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?2π
8.铁路在弯道处的内外轨道高度是不同的,如图所示,已知内外轨道平面对水平面倾角为θ,弯道处的圆弧半径为R,在转弯时的速度为下列情况时,正确的是(??
)
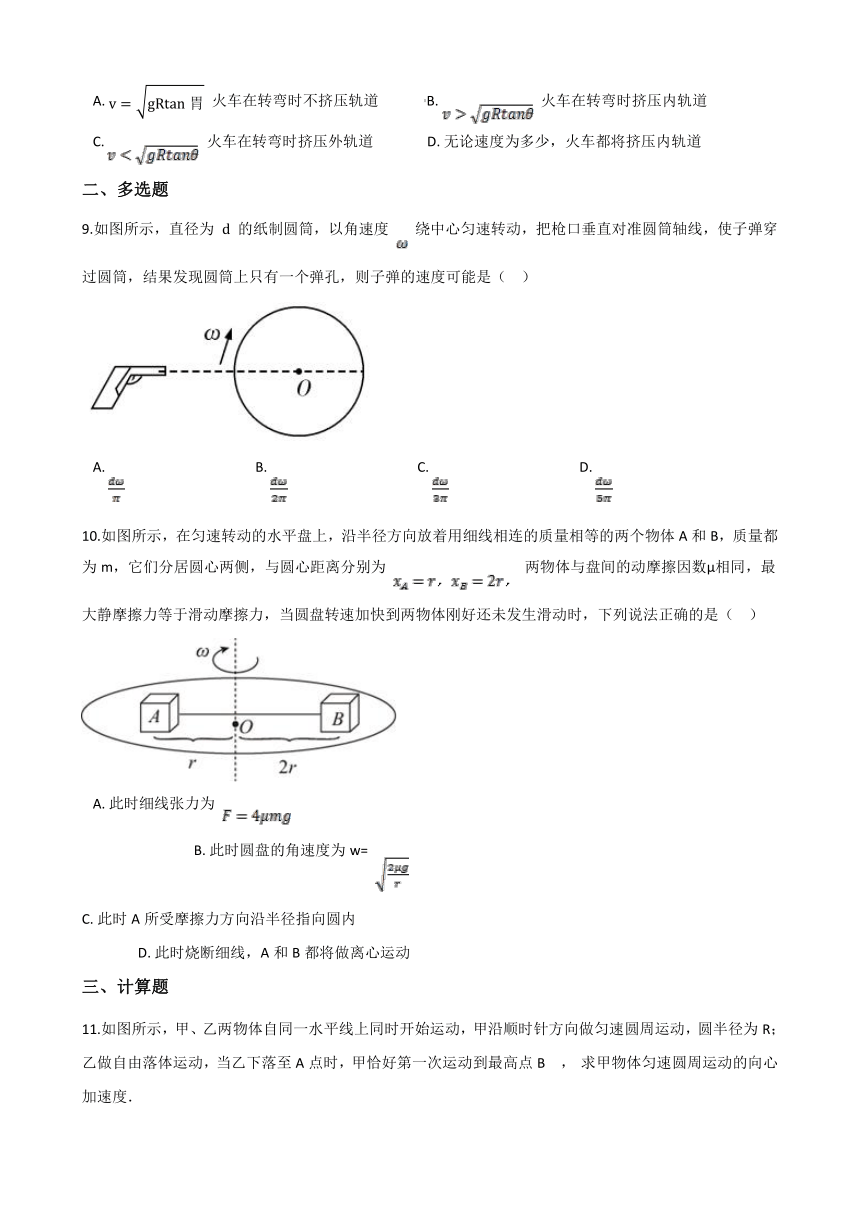
A.?
火车在转弯时不挤压轨道?????????????B.?
火车在转弯时挤压内轨道
C.?
火车在转弯时挤压外轨道???????????????D.?无论速度为多少,火车都将挤压内轨道
二、多选题
9.如图所示,直径为
的纸制圆筒,以角速度
绕中心匀速转动,把枪口垂直对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,则子弹的速度可能是(
??)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
10.如图所示,在匀速转动的水平盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,质量都为m,它们分居圆心两侧,与圆心距离分别为
两物体与盘间的动摩擦因数μ相同,最大静摩擦力等于滑动摩擦力,当圆盘转速加快到两物体刚好还未发生滑动时,下列说法正确的是(??
)
A.?此时细线张力为
????????????????????????????????B.?此时圆盘的角速度为w=
C.?此时A所受摩擦力方向沿半径指向圆内
????????????????D.?此时烧断细线,A和B都将做离心运动
三、计算题
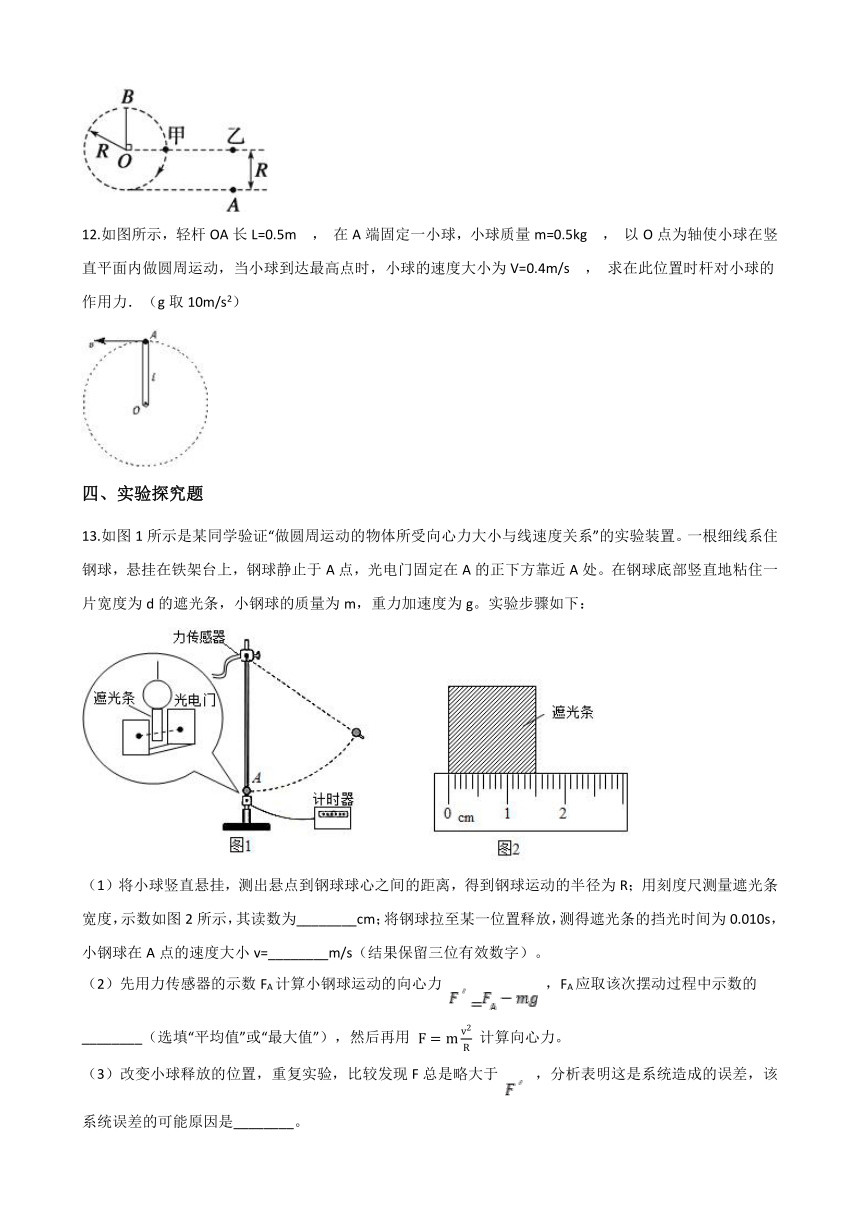
11.如图所示,甲、乙两物体自同一水平线上同时开始运动,甲沿顺时针方向做匀速圆周运动,圆半径为R;乙做自由落体运动,当乙下落至A点时,甲恰好第一次运动到最高点B
,
求甲物体匀速圆周运动的向心加速度.
12.如图所示,轻杆OA长L=0.5m
,
在A端固定一小球,小球质量m=0.5kg
,
以O点为轴使小球在竖直平面内做圆周运动,当小球到达最高点时,小球的速度大小为V=0.4m/s
,
求在此位置时杆对小球的作用力.(g取10m/s2)
四、实验探究题
13.如图1所示是某同学验证“做圆周运动的物体所受向心力大小与线速度关系”的实验装置。一根细线系住钢球,悬挂在铁架台上,钢球静止于A点,光电门固定在A的正下方靠近A处。在钢球底部竖直地粘住一片宽度为d的遮光条,小钢球的质量为m,重力加速度为g。实验步骤如下:
(1)将小球竖直悬挂,测出悬点到钢球球心之间的距离,得到钢球运动的半径为R;用刻度尺测量遮光条宽度,示数如图2所示,其读数为________cm;将钢球拉至某一位置释放,测得遮光条的挡光时间为0.010s,小钢球在A点的速度大小v=________m/s(结果保留三位有效数字)。
(2)先用力传感器的示数FA计算小钢球运动的向心力
,FA应取该次摆动过程中示数的________(选填“平均值”或“最大值”),然后再用
计算向心力。
(3)改变小球释放的位置,重复实验,比较发现F总是略大于
,分析表明这是系统造成的误差,该系统误差的可能原因是________。
A.小钢球的质量偏大
B.小钢球初速不为零
C.总是存在空气阻力
D.速度的测量值偏大
(4)为了消除该系统误差,可以________(回答一条即可)。
14.如图甲所示是某同学探究做圆周运动的物体质量、向心力、轨道半径及线速度关系的实验装置,圆柱体放置在水平光滑圆盘上做匀速圆周运动
力传感器测量向心力F,速度传感器测量圆柱体的线速度v,该同学通过保持圆柱体质量和运动半径不变,来探究向心力F与线速度v的关系:
(1)该同学采用的实验方法为________。
A.等效替代法
B.控制变量法
C.理想化模型法
(2)改变线速度v,多次测量,该同学测出了五组F、v数据,如表所示:
①作出
图线如图乙所示;
②若圆柱体运动半径
,由作出的
的图线可得圆柱体的质量
________kg。(结果保留两位有效数字)
答案解析部分
一、单选题
1.
C
解析:A.A,B两处装饰物绕同一轴转动,则周期相等,A不符合题意;
B.根据a=ω2r可知,A,B两处装饰物的向心加速度大小之比为2:1,B不符合题意;
C.根据v=ωr可知,A,B两处装饰物的线速度大小之比为2:1,C符合题意;
D.根据F=ma可知,A,B两处装饰物受到的向心力大小之比为1:1,D不符合题意。
故答案为:C。
分析:AB两点其角速度相等,所以线速度相等;利用半径的比值可以求出加速度和线速度的比值;利用加速度和质量的比值可以求出向心力的比值。
2.
D
解析:AB.设自行车的速度为v,摩擦轮的半径为r,则后轮、摩擦轮的速度都等于v,线圈转动产生正弦电流,周期
,v加倍,T减小为原来的
,A、B不符合题意;
CD.若线圈的匝数为N、面积为S、磁感应强度为B,则线圈产生的电动势最大值
有效值为
小灯泡的电功率
C不符合题意,D符合题意。
故答案为:D。
分析:根据线速度与周期的关系求出速度加倍后的周期,根据感应电动势最大值求出有效值,从而求出小灯泡的功率。
3.
A
解析:三个轮相互不打滑,则三轮边缘处线速度的大小相等。都等于甲轮边缘的线速度,根据角速度与线速度的关系式得线速度为r1ω。
故答案为:A。
分析:由于边缘处线速度相等,所以利用角速度和半径可以求出线速度的大小。
4.
C
解析:A.在汽车不离开地面的前提下,有
再由牛顿第三定律可知,汽车的速度越大,汽车对地面的压力就越小,A不符合题意;
BC.以驾驶员为分析对象,则有
再由牛顿第三定律可知,只要汽车行驶,驾驶员对座椅的压力大小都小于他自身的重力,B不符合题意、C符合题意;
D.如果某时刻速度增大到使汽车对地面压力为零,则此时驾驶员对座椅的压力也为零,驾驶员会有失重的感觉,D不符合题意。
故答案为:C。
分析:把地球看成一个巨大的拱形桥,汽车做圆周运动,由地面的支持力和重力提供汽车所需要的向心力,根据牛顿第二定律列式分别分析即可判断。
5.
C
解析:物体在其轨迹最高点P处只有水平速度,其水平速度大小为
,在最高点,把物体的运动看成圆周运动的一部分,物体的重力作为向心力,由向心力的公式得
,所以在其轨迹最高点P处的曲率半径是:
,C符合题意.
故答案为:C
分析:根据合力提供向心力求出P处的曲率半径。
6.
D
解析:A.物块向右匀速运动时,则夹子与物体M,处于平衡状态,那么绳中的张力等于Mg,A不符合题意;
B.小环碰到钉子P时,物体M做圆周运动,依据最低点由拉力与重力的合力提供向心力,因此绳中的张力大于Mg,而与2F大小关系不确定,B不符合题意;
C.小环碰到钉子P时,绳子的力与重力均在竖直方向,故物块运动速度不变,C不符合题意;
D.因为夹子对物体M的最大静摩擦力为2F,根据据牛顿第二定律,结合向心力表达式,对物体M,则有:
解得:
D符合题意;
故答案为:D。
分析:根据平衡求出向右匀速运动时绳子的张力;再根据合力提供向心力求出最大速度。
7.
C
解析:解:设小球与圆心连线与竖直方向的夹角为θ,受力如图所示,根据牛顿第二定律得:
mgtanθ=mr(2πn)2
,
根据几何关系知,h=R﹣Rcosθ,r=Rsinθ,
解得转速n=
,C符合题意,A、B、D不符合题意.
故答案为:C.
分析:首先以小球为研究对象进行受力分析,明确向心力的来源结合几何关系,求出匀速圆周运动的半径,利用向心力公式求解。
8.
A
解析:解:A、火车以某一速度v通过某弯道时,内、外轨道均不受侧压力作用,其所受的重力和支持力的合力提供向心力,由图可以得:
F合=mgtanθ(θ为轨道平面与水平面的夹角)
合力等于向心力,故有:mgtanθ=
,
解得v=
,当
火车在转弯时不挤压轨道,A符合题意.
B、当
,重力和支持力的合力不够提供向心力,则火车拐弯时会挤压外轨,B不符合题意.
C、当
,重力和支持力的合力大于向心力,则火车拐弯时会挤压内轨,CD不符合题意.
故选:A.
分析:重力和支持力的合力提供向心力是解题关键,由于具体数值未知应该分情况判断。
二、多选题
9.
A,C,D
解析:在子弹飞行的时间内,圆筒转动的角度为
,
则时间为:
,
所以子弹的速度为:
当
时,
当
时,
当
时,
故答案为:ACD
分析:子弹沿圆筒直径穿过圆筒,圆筒转动的角度为
,
结合角速度求出时间,从而得出子弹的速度。
10.
B,D
解析:ABC.两物块A和B随着圆盘转动时,角速度相同,根据
可知B的半径比A的半径大,所以B所需向心力大,绳子拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,B的静摩擦力方向指向圆心,A的最大静摩擦力方向指向圆外。根据牛顿第二定律
对A有
对B有
联立解得
AC不符合题意,B符合题意;
D.若此时剪断绳子,B的摩擦力不足以提供所需的向心力,B将会做离心运动,此时A所需要的向心力将角速度值代入可求得
由此可知A的摩擦力也不足以提供所需的向心力,A也将会做离心运动,D符合题意。
故答案为:BD。
分析:对A、B进行受力分析,根据合力提供向心力,从而求出角速度,根据合力与向心力的大小判断A是否做离心运动。
三、计算题
11.解:设乙下落到A点的时间为t
,
则对乙满足R=
gt2
,
得t=
;
这段时间内甲运动了
T
,
即
T=
;
又由于an=ω2R=
R
,
由①②得:an=
π2g?
解析:设乙下落到A点的时间为t
,
则对乙满足R=
gt2
,
得t=
;
这段时间内甲运动了
T
,
即
T=
;
又由于an=ω2R=
R
,
由①②得:an=
π2g
答:甲物体匀速圆周运动的向心加速度为
π2g
.
分析:根据自由落体运动求出时间,根据等时性求解周期,根据向心加速度定义公式求出向心加速度.
12.小球所需向心力为:F向=m
=0.16N
小球受重力为:mg=0.5×10N=5N
重力大于所需向心力,所以杆对小球有竖直向上的作用力F,以竖直向下为正方向,对小球有:
mg﹣F=F向
解得:F=4.84N
.
解析:小球所需向心力为:F向=m
=0.16N
小球受重力为:mg=0.5×10N=5N
重力大于所需向心力,所以杆对小球有竖直向上的作用力F,以竖直向下为正方向,对小球有:
mg﹣F=F向
解得:F=4.84N
.
答:此位置时杆对小球的作用力为4.84N
,
方向向上.
分析:小球在最高点靠重力和杆的作用力的合力提供向心力,根据牛顿第二定律求出杆对小球的作用力.
四、实验探究题
13.
(1)1.50(1.49-1.51);1.50(1.49-1.51)
(2)最大值
(3)D
(4)测出光电门发光孔到悬点的距离L,由
,求出小球的准确速度(将悬线变长一些、遮光条长度变短不得分)
解析:(1)根据刻度尺数据可直接读出,读数为1.50cm。根据速度公式可得
(2)因为只有力传感器的示数FA最大时,小球在最低点,此时才能满足
。(3)因为
,当速度测量值偏大时,F偏大,此时F才略大于
,故答案为:D。(4)为了消除该系统误差,可以减小速度误差,测出光电门发光孔到悬点的距离L,由
,求出小球的准确速度。
分析:(1)利用刻度尺的分度值可以读出对应的读数;结合平均速度公式可以求出速度的大小;
(2)利用传感器的数值最大时,其拉力和重力的合力才完全提供向心力;
(3)利用向心力的表达式可以判别向心力测量值偏大的原因。
14.
(1)B
(2)
(0.17-0.19均可)
解析:(1)实验中研究向心力和速度的关系,保持圆柱体质量和运动半径不变,采用的实验方法是控制变量法,故答案为:B;(2)②根据
知,图线的斜率
则有
代入数据解得
分析:(1)研究向心力和速度的关系需要采用控制变量法;
(2)利用图像斜率结合向心力表达式可以求出质量的大小。
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
第三章
圆周运动单元测试(提高版)
一、单选题
1.为欢度春节,某酒店的旋转门上A,B两点粘贴着小型装饰物(视为质点)可绕中心轴转动,
到中心轴的距离为
到中心轴距离的两倍,
处装饰物的质量为
处装饰物质量的两倍,如图所示。当旋转门匀速转动时,下列说法正确的是(??
)
A.?A,B两处装饰物的周期之比为
B.?A,B两处装饰物的向心加速度大小之比为
C.?A,B两处装饰物的线速度大小之比为
D.?A,B两处装饰物受到的向心力大小之比为
2.有一种自行车,它有能向车头灯泡供电的小型发电机,其原理示意图如图甲所示:图中N、S是一对固定的磁极,磁极间有一固定在绝缘转轴上的矩形线圈,转轴的一端有一个与自行车后轮边缘接触的摩擦轮。如图乙所示,当车轮转动时,因摩擦而带动摩擦轮转动,从而使线圈在磁场中转动而产生电流给车头灯泡供电。关于此装置,下列说法正确的是(??
)
A.?自行车的速度加倍,线圈中交变电流的周期加倍
B.?自行车的速度加倍,线圈中交变电流的周期不变
C.?小灯泡的电功率与自行车的速度成正比
D.?小灯泡的电功率与自行车速度的平方成正比
3.某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3
,
若甲轮匀速转动角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的线速度大小为(??
)
A.?r1ω?????????????????????????????????????B.?r2ω?????????????????????????????????????C.?r3ω?????????????????????????????????????D.?
4.如图所示,地球可以看成一个巨大的拱形桥,桥面半径R=6400km,地面上行驶的汽车中驾驶员的重力G=800N,在汽车不离开地面的前提下,下列分析中正确的是(??
)
A.?汽车的速度越大,则汽车对地面的压力也越大
B.?不论汽车的行驶速度如何,驾驶员对座椅压力大小都等于800N
C.?只要汽车行驶,驾驶员对座椅压力大小都小于他自身的重力
D.?如果某时刻速度增大到使汽车对地面压力为零,则此时驾驶员会有超重的感觉
5.一般的曲线运动可以分成很多小段,每小段都可以看成圆周运动的一部分,即把整条曲线用一系列不同半径的小圆弧来代替.如图(a)所示,曲线上的A点的曲率圆定义为:通过A点和曲线上紧邻A点两侧的两点作一圆,在极限情况下,这个圆就叫做A点的曲率圆,其半径ρ叫做A点的曲率半径.现将一物体沿与水平面成α角的方向已速度υ0抛出,如图(b)所示.则在其轨迹最高点P处的曲率半径是(??
)
A.???????????????????????????????B.?
??????????????????????????????C.???????????????????????????????D.?
6.如图所示,一小物块被夹子夹紧,夹子通过轻绳悬挂在小环上,小环套在水平光滑细杆上。物块质量为M,到小环的距离为L,其两侧面与夹子间的最大静摩擦力均为F。小环和物块以速度v向右匀速运动,小环碰到杆上的钉子P后立刻停止,物块向上摆动。整个过程中,物块在夹子中没有滑动。小环和夹子的质量均不计,重力加速度为g。下列说法正确的是(??
)
A.?物块向右匀速运动时,绳中的张力等于2F
???????????B.?小环碰到钉子P时,绳中的张力大于2F
C.?小环碰到钉子P时,物块运动速度立即减小
?????????D.?速度v不能超过
7.如图所示,光滑半圆形碗固定在地面上,其半径为R,一质量为m的小球紧贴碗的内表面做匀速圆周运动,其轨道平面水平且距离碗底的高度为h,重力加速度为g,则小球做匀速圆周运动的转速为(单位r/s)(??
)
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?2π
8.铁路在弯道处的内外轨道高度是不同的,如图所示,已知内外轨道平面对水平面倾角为θ,弯道处的圆弧半径为R,在转弯时的速度为下列情况时,正确的是(??
)
A.?
火车在转弯时不挤压轨道?????????????B.?
火车在转弯时挤压内轨道
C.?
火车在转弯时挤压外轨道???????????????D.?无论速度为多少,火车都将挤压内轨道
二、多选题
9.如图所示,直径为
的纸制圆筒,以角速度
绕中心匀速转动,把枪口垂直对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,则子弹的速度可能是(
??)
A.???????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
10.如图所示,在匀速转动的水平盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,质量都为m,它们分居圆心两侧,与圆心距离分别为
两物体与盘间的动摩擦因数μ相同,最大静摩擦力等于滑动摩擦力,当圆盘转速加快到两物体刚好还未发生滑动时,下列说法正确的是(??
)
A.?此时细线张力为
????????????????????????????????B.?此时圆盘的角速度为w=
C.?此时A所受摩擦力方向沿半径指向圆内
????????????????D.?此时烧断细线,A和B都将做离心运动
三、计算题
11.如图所示,甲、乙两物体自同一水平线上同时开始运动,甲沿顺时针方向做匀速圆周运动,圆半径为R;乙做自由落体运动,当乙下落至A点时,甲恰好第一次运动到最高点B
,
求甲物体匀速圆周运动的向心加速度.
12.如图所示,轻杆OA长L=0.5m
,
在A端固定一小球,小球质量m=0.5kg
,
以O点为轴使小球在竖直平面内做圆周运动,当小球到达最高点时,小球的速度大小为V=0.4m/s
,
求在此位置时杆对小球的作用力.(g取10m/s2)
四、实验探究题
13.如图1所示是某同学验证“做圆周运动的物体所受向心力大小与线速度关系”的实验装置。一根细线系住钢球,悬挂在铁架台上,钢球静止于A点,光电门固定在A的正下方靠近A处。在钢球底部竖直地粘住一片宽度为d的遮光条,小钢球的质量为m,重力加速度为g。实验步骤如下:
(1)将小球竖直悬挂,测出悬点到钢球球心之间的距离,得到钢球运动的半径为R;用刻度尺测量遮光条宽度,示数如图2所示,其读数为________cm;将钢球拉至某一位置释放,测得遮光条的挡光时间为0.010s,小钢球在A点的速度大小v=________m/s(结果保留三位有效数字)。
(2)先用力传感器的示数FA计算小钢球运动的向心力
,FA应取该次摆动过程中示数的________(选填“平均值”或“最大值”),然后再用
计算向心力。
(3)改变小球释放的位置,重复实验,比较发现F总是略大于
,分析表明这是系统造成的误差,该系统误差的可能原因是________。
A.小钢球的质量偏大
B.小钢球初速不为零
C.总是存在空气阻力
D.速度的测量值偏大
(4)为了消除该系统误差,可以________(回答一条即可)。
14.如图甲所示是某同学探究做圆周运动的物体质量、向心力、轨道半径及线速度关系的实验装置,圆柱体放置在水平光滑圆盘上做匀速圆周运动
力传感器测量向心力F,速度传感器测量圆柱体的线速度v,该同学通过保持圆柱体质量和运动半径不变,来探究向心力F与线速度v的关系:
(1)该同学采用的实验方法为________。
A.等效替代法
B.控制变量法
C.理想化模型法
(2)改变线速度v,多次测量,该同学测出了五组F、v数据,如表所示:
①作出
图线如图乙所示;
②若圆柱体运动半径
,由作出的
的图线可得圆柱体的质量
________kg。(结果保留两位有效数字)
答案解析部分
一、单选题
1.
C
解析:A.A,B两处装饰物绕同一轴转动,则周期相等,A不符合题意;
B.根据a=ω2r可知,A,B两处装饰物的向心加速度大小之比为2:1,B不符合题意;
C.根据v=ωr可知,A,B两处装饰物的线速度大小之比为2:1,C符合题意;
D.根据F=ma可知,A,B两处装饰物受到的向心力大小之比为1:1,D不符合题意。
故答案为:C。
分析:AB两点其角速度相等,所以线速度相等;利用半径的比值可以求出加速度和线速度的比值;利用加速度和质量的比值可以求出向心力的比值。
2.
D
解析:AB.设自行车的速度为v,摩擦轮的半径为r,则后轮、摩擦轮的速度都等于v,线圈转动产生正弦电流,周期
,v加倍,T减小为原来的
,A、B不符合题意;
CD.若线圈的匝数为N、面积为S、磁感应强度为B,则线圈产生的电动势最大值
有效值为
小灯泡的电功率
C不符合题意,D符合题意。
故答案为:D。
分析:根据线速度与周期的关系求出速度加倍后的周期,根据感应电动势最大值求出有效值,从而求出小灯泡的功率。
3.
A
解析:三个轮相互不打滑,则三轮边缘处线速度的大小相等。都等于甲轮边缘的线速度,根据角速度与线速度的关系式得线速度为r1ω。
故答案为:A。
分析:由于边缘处线速度相等,所以利用角速度和半径可以求出线速度的大小。
4.
C
解析:A.在汽车不离开地面的前提下,有
再由牛顿第三定律可知,汽车的速度越大,汽车对地面的压力就越小,A不符合题意;
BC.以驾驶员为分析对象,则有
再由牛顿第三定律可知,只要汽车行驶,驾驶员对座椅的压力大小都小于他自身的重力,B不符合题意、C符合题意;
D.如果某时刻速度增大到使汽车对地面压力为零,则此时驾驶员对座椅的压力也为零,驾驶员会有失重的感觉,D不符合题意。
故答案为:C。
分析:把地球看成一个巨大的拱形桥,汽车做圆周运动,由地面的支持力和重力提供汽车所需要的向心力,根据牛顿第二定律列式分别分析即可判断。
5.
C
解析:物体在其轨迹最高点P处只有水平速度,其水平速度大小为
,在最高点,把物体的运动看成圆周运动的一部分,物体的重力作为向心力,由向心力的公式得
,所以在其轨迹最高点P处的曲率半径是:
,C符合题意.
故答案为:C
分析:根据合力提供向心力求出P处的曲率半径。
6.
D
解析:A.物块向右匀速运动时,则夹子与物体M,处于平衡状态,那么绳中的张力等于Mg,A不符合题意;
B.小环碰到钉子P时,物体M做圆周运动,依据最低点由拉力与重力的合力提供向心力,因此绳中的张力大于Mg,而与2F大小关系不确定,B不符合题意;
C.小环碰到钉子P时,绳子的力与重力均在竖直方向,故物块运动速度不变,C不符合题意;
D.因为夹子对物体M的最大静摩擦力为2F,根据据牛顿第二定律,结合向心力表达式,对物体M,则有:
解得:
D符合题意;
故答案为:D。
分析:根据平衡求出向右匀速运动时绳子的张力;再根据合力提供向心力求出最大速度。
7.
C
解析:解:设小球与圆心连线与竖直方向的夹角为θ,受力如图所示,根据牛顿第二定律得:
mgtanθ=mr(2πn)2
,
根据几何关系知,h=R﹣Rcosθ,r=Rsinθ,
解得转速n=
,C符合题意,A、B、D不符合题意.
故答案为:C.
分析:首先以小球为研究对象进行受力分析,明确向心力的来源结合几何关系,求出匀速圆周运动的半径,利用向心力公式求解。
8.
A
解析:解:A、火车以某一速度v通过某弯道时,内、外轨道均不受侧压力作用,其所受的重力和支持力的合力提供向心力,由图可以得:
F合=mgtanθ(θ为轨道平面与水平面的夹角)
合力等于向心力,故有:mgtanθ=
,
解得v=
,当
火车在转弯时不挤压轨道,A符合题意.
B、当
,重力和支持力的合力不够提供向心力,则火车拐弯时会挤压外轨,B不符合题意.
C、当
,重力和支持力的合力大于向心力,则火车拐弯时会挤压内轨,CD不符合题意.
故选:A.
分析:重力和支持力的合力提供向心力是解题关键,由于具体数值未知应该分情况判断。
二、多选题
9.
A,C,D
解析:在子弹飞行的时间内,圆筒转动的角度为
,
则时间为:
,
所以子弹的速度为:
当
时,
当
时,
当
时,
故答案为:ACD
分析:子弹沿圆筒直径穿过圆筒,圆筒转动的角度为
,
结合角速度求出时间,从而得出子弹的速度。
10.
B,D
解析:ABC.两物块A和B随着圆盘转动时,角速度相同,根据
可知B的半径比A的半径大,所以B所需向心力大,绳子拉力相等,所以当圆盘转速加快到两物体刚好还未发生滑动时,B的静摩擦力方向指向圆心,A的最大静摩擦力方向指向圆外。根据牛顿第二定律
对A有
对B有
联立解得
AC不符合题意,B符合题意;
D.若此时剪断绳子,B的摩擦力不足以提供所需的向心力,B将会做离心运动,此时A所需要的向心力将角速度值代入可求得
由此可知A的摩擦力也不足以提供所需的向心力,A也将会做离心运动,D符合题意。
故答案为:BD。
分析:对A、B进行受力分析,根据合力提供向心力,从而求出角速度,根据合力与向心力的大小判断A是否做离心运动。
三、计算题
11.解:设乙下落到A点的时间为t
,
则对乙满足R=
gt2
,
得t=
;
这段时间内甲运动了
T
,
即
T=
;
又由于an=ω2R=
R
,
由①②得:an=
π2g?
解析:设乙下落到A点的时间为t
,
则对乙满足R=
gt2
,
得t=
;
这段时间内甲运动了
T
,
即
T=
;
又由于an=ω2R=
R
,
由①②得:an=
π2g
答:甲物体匀速圆周运动的向心加速度为
π2g
.
分析:根据自由落体运动求出时间,根据等时性求解周期,根据向心加速度定义公式求出向心加速度.
12.小球所需向心力为:F向=m
=0.16N
小球受重力为:mg=0.5×10N=5N
重力大于所需向心力,所以杆对小球有竖直向上的作用力F,以竖直向下为正方向,对小球有:
mg﹣F=F向
解得:F=4.84N
.
解析:小球所需向心力为:F向=m
=0.16N
小球受重力为:mg=0.5×10N=5N
重力大于所需向心力,所以杆对小球有竖直向上的作用力F,以竖直向下为正方向,对小球有:
mg﹣F=F向
解得:F=4.84N
.
答:此位置时杆对小球的作用力为4.84N
,
方向向上.
分析:小球在最高点靠重力和杆的作用力的合力提供向心力,根据牛顿第二定律求出杆对小球的作用力.
四、实验探究题
13.
(1)1.50(1.49-1.51);1.50(1.49-1.51)
(2)最大值
(3)D
(4)测出光电门发光孔到悬点的距离L,由
,求出小球的准确速度(将悬线变长一些、遮光条长度变短不得分)
解析:(1)根据刻度尺数据可直接读出,读数为1.50cm。根据速度公式可得
(2)因为只有力传感器的示数FA最大时,小球在最低点,此时才能满足
。(3)因为
,当速度测量值偏大时,F偏大,此时F才略大于
,故答案为:D。(4)为了消除该系统误差,可以减小速度误差,测出光电门发光孔到悬点的距离L,由
,求出小球的准确速度。
分析:(1)利用刻度尺的分度值可以读出对应的读数;结合平均速度公式可以求出速度的大小;
(2)利用传感器的数值最大时,其拉力和重力的合力才完全提供向心力;
(3)利用向心力的表达式可以判别向心力测量值偏大的原因。
14.
(1)B
(2)
(0.17-0.19均可)
解析:(1)实验中研究向心力和速度的关系,保持圆柱体质量和运动半径不变,采用的实验方法是控制变量法,故答案为:B;(2)②根据
知,图线的斜率
则有
代入数据解得
分析:(1)研究向心力和速度的关系需要采用控制变量法;
(2)利用图像斜率结合向心力表达式可以求出质量的大小。
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
