1.3.1函数的单调性与导数1-2020-2021学年人教A版高中数学选修2-2课件(21张PPT)
文档属性
| 名称 | 1.3.1函数的单调性与导数1-2020-2021学年人教A版高中数学选修2-2课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 890.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 21:03:23 | ||
图片预览






文档简介
1.3.1函数的单调性与导数
函数y=f(x)在给定区间G上,当x1、x2∈G且x1<x2时,
(1)都有f(x1)<f(x2),
则f(x)在G上是增函数;
(2)都有f(x1)>f(x2),
则f(x)在G上是减函数;
一、复习引入:
①函数单调性判定(定义法)
则f(x)在G上是增函数;
则f(x)在G上是减函数;
y
x
o
a
b
y
x
o
a
b
若f(x)在G上是增函数或减函数,则f(x)在G上具有严格的单调性。G称为单调区间.
G = (a,b)
一、复习引入:
②函数单调性判定(图象法)
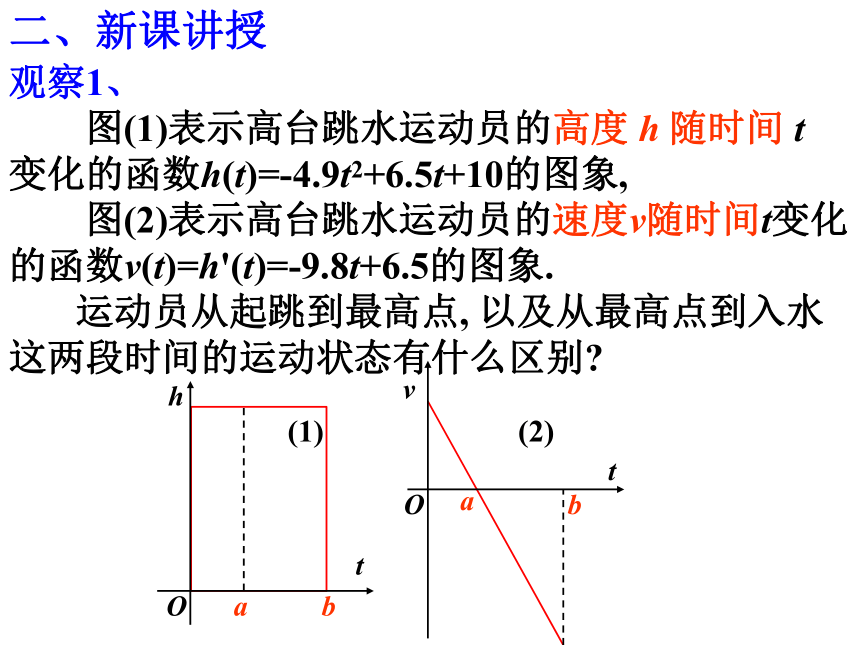
观察1、
图(1)表示高台跳水运动员的高度 h 随时间 t 变化的函数h(t)=-4.9t2+6.5t+10的图象,
图(2)表示高台跳水运动员的速度v随时间t变化的函数v(t)=h'(t)=-9.8t+6.5的图象.
运动员从起跳到最高点, 以及从最高点到入水这两段时间的运动状态有什么区别?
a
a
b
b
t
t
v
h
O
O
(1)
(2)
二、新课讲授
a
a
b
b
t
t
v
h
O
O
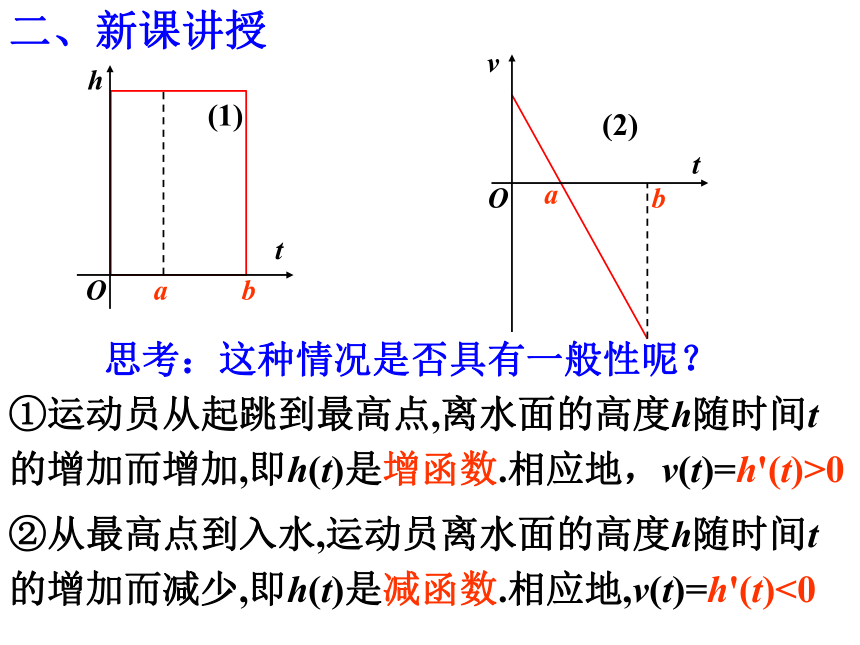
②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,v(t)=h'(t)<0
(1)
(2)
①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,v(t)=h'(t)>0
二、新课讲授
思考:这种情况是否具有一般性呢?
x
y
O
x
y
O
x
y
O
x
y
O
y = x
y = x2
y = x3
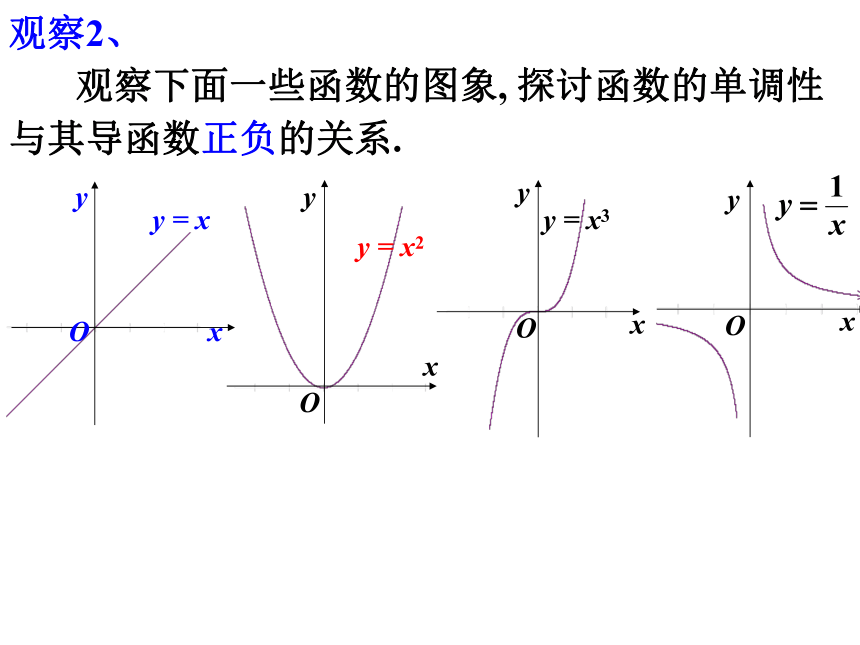
观察2、
观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.
在某个区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间内单调递增; 如果f'(x)<0,那么函数y=f(x)在这个区间内单调递减.
由上我们可得以下的结论:
探究
1、如果在某区间内恒有f'(x)=0,那么函数f(x)有什么特性?
如果在某个区间内恒有f'(x)=0,则f(x)为常数函数.
2.在某区间内f'(x)>0是f(x)在此区间上为增函数的什么条件?
充分非必要条件.
如果在某个区间内恒有 ,则 为常数函数.
2.在某区间内 是 在此区间上为增函数的什么条件?
1.如果在某区间内恒有 ,那么函数 有什么特性?
充分非必要条件. 课本p23
则 f ( x ) 在G 上是增函数;
则 f ( x ) 在G 上是减函数;
定义上理解单调区间与函数的导数的关系
二、新课讲解:
我们已经知道,曲线y=f(x)的切线的斜率就是函数y=
f(x)的导数.
从函数y=x2的图像可以看到:
y
x
o
1
1
-1
在区间(0,+∞)内,切线的斜率为正,函数y=f(x)的值随着x的增大而增大,即 >0 时,函数y=f(x) 在区间(0, +∞)内为增函数.
在区间(-∞,0)内,切线的斜率为负,函数y=f(x)的值随着x的增大而减小,即 <0 时,函数y=f(x) 在区间(-∞,0)内为减函数.
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,如果在 这个区间内 >0,那么函数y=f(x) 在这个区间内为增函数;如果在这个区间内 <0,那么函数y=f(x) 在这个区间内为减函数.
由上我们可得以下的结论:
例1、已知导函数f'(x)的下列信息:
当10;
当x>4 , 或x<1时,f'(x)<0;
当x=4 , 或x=1时,f'(x)=0.
试画出函数f(x)的图象的大致形状.
x
y
O
1
4
解: 当10可知f(x)在此区间内单调递增;
当x>4 , 或x<1时, f'(x)<0可知f(x)在此区间内单调递减;
当x=4 , 或x=1时, f'(x)=0
综上, 函数f(x)图象的大致
形状如右图所示.
三、例题讲解
例2、判断下列函数的单调性, 并求出单调区间:
解:
(1) 因为f(x)=x3+3x, 所以f'(x)=3x2+3=3(x2+1)>0.
因此, 函数f(x)=x3+3x在x∈R上单调递增.
(2) 因为f(x)=x2-2x-3, 所以f'(x)=2x-2=(2x-1).
当f'(x)>0,即x>1时,函数f(x)=x2-2x-3单调递增;
当f'(x)<0,即x<1时,函数f(x)=x2-2x-3单调递减.
解:
例2、判断下列函数的单调性, 并求出单调区间:
2°求可导函数f(x)单调区间的步骤:
①求定义域
②求f'(x)
③令f'(x)>0解不等式?f(x)的递增区间
f'(x)<0解不等式?f(x)的递减区间
④求单调区间
归纳:
1°什么情况下,用“导数法” 求函数单调性、单调区间较简便?
总结: 当遇到三次或三次以上的,或图象很难画出的函数求单调性问题时,应考虑导数法。
例3、已知函数 ,试讨论出此函数的单调区间.并作出图像
四、课堂练习
1、判断下列函数的单调性, 并求出单调区间:
注: 如果一个函数具有相同单调性的单调区间不止一个,这些单调区间一般不能用“∪”连接,而只能用“逗号”或“和”分开。
2、证明函数f(x)=2x3-6x2+7在(0,2)内是减函数
证明:∵f(x)=2x3-6x2+7,∴f'(x)=6x2-12x
由f'(x)<0,解得0所以函数f(x)的递减区间是(0,2),
即函数f(x)在(0,2)内是减函数.
注:证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求f'(x)
(2)确认f'(x)在(a,b)内的符号
(3)作出结论
2、证明函数f(x)=2x3-6x2+7在(0,2)内是减函数
3、若在区间(a,b)内有f'(x)>0,且f(a)≥0,则在(a,b)内有( )
A.f(x)>0 B.f(x)<0 C.f(x)=0 D.不能确定
4、函数f(x)=-2x+lnx的增区间是_______,减区间是______
5、已知f(x)=x2+2xf'(1),则f'(1)等于_______
6、求下列函数的单调区间
A
-2
7、确定下列函数的单调区间:
注意到函数的定义域是(-1,+∞),故f(x)的递增区间是(1,+∞);
由f'(x)<0解得-1说明:函数的单调区间必定是它的定义域的子区间,故求函数的单调区间一定首先要确定函数的定义域,在求出使导数的值为正或负的x的范围时,要与定义域求两者的交集.
函数y=f(x)在给定区间G上,当x1、x2∈G且x1<x2时,
(1)都有f(x1)<f(x2),
则f(x)在G上是增函数;
(2)都有f(x1)>f(x2),
则f(x)在G上是减函数;
一、复习引入:
①函数单调性判定(定义法)
则f(x)在G上是增函数;
则f(x)在G上是减函数;
y
x
o
a
b
y
x
o
a
b
若f(x)在G上是增函数或减函数,则f(x)在G上具有严格的单调性。G称为单调区间.
G = (a,b)
一、复习引入:
②函数单调性判定(图象法)
观察1、
图(1)表示高台跳水运动员的高度 h 随时间 t 变化的函数h(t)=-4.9t2+6.5t+10的图象,
图(2)表示高台跳水运动员的速度v随时间t变化的函数v(t)=h'(t)=-9.8t+6.5的图象.
运动员从起跳到最高点, 以及从最高点到入水这两段时间的运动状态有什么区别?
a
a
b
b
t
t
v
h
O
O
(1)
(2)
二、新课讲授
a
a
b
b
t
t
v
h
O
O
②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,v(t)=h'(t)<0
(1)
(2)
①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,v(t)=h'(t)>0
二、新课讲授
思考:这种情况是否具有一般性呢?
x
y
O
x
y
O
x
y
O
x
y
O
y = x
y = x2
y = x3
观察2、
观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.
在某个区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间内单调递增; 如果f'(x)<0,那么函数y=f(x)在这个区间内单调递减.
由上我们可得以下的结论:
探究
1、如果在某区间内恒有f'(x)=0,那么函数f(x)有什么特性?
如果在某个区间内恒有f'(x)=0,则f(x)为常数函数.
2.在某区间内f'(x)>0是f(x)在此区间上为增函数的什么条件?
充分非必要条件.
如果在某个区间内恒有 ,则 为常数函数.
2.在某区间内 是 在此区间上为增函数的什么条件?
1.如果在某区间内恒有 ,那么函数 有什么特性?
充分非必要条件. 课本p23
则 f ( x ) 在G 上是增函数;
则 f ( x ) 在G 上是减函数;
定义上理解单调区间与函数的导数的关系
二、新课讲解:
我们已经知道,曲线y=f(x)的切线的斜率就是函数y=
f(x)的导数.
从函数y=x2的图像可以看到:
y
x
o
1
1
-1
在区间(0,+∞)内,切线的斜率为正,函数y=f(x)的值随着x的增大而增大,即 >0 时,函数y=f(x) 在区间(0, +∞)内为增函数.
在区间(-∞,0)内,切线的斜率为负,函数y=f(x)的值随着x的增大而减小,即 <0 时,函数y=f(x) 在区间(-∞,0)内为减函数.
a
b
y=f(x)
x
o
y
y=f(x)
x
o
y
a
b
f '(x)>0
f '(x)<0
定义:一般地,设函数y=f(x)在某个区间(a,b)内有导数,如果在 这个区间内 >0,那么函数y=f(x) 在这个区间内为增函数;如果在这个区间内 <0,那么函数y=f(x) 在这个区间内为减函数.
由上我们可得以下的结论:
例1、已知导函数f'(x)的下列信息:
当1
当x>4 , 或x<1时,f'(x)<0;
当x=4 , 或x=1时,f'(x)=0.
试画出函数f(x)的图象的大致形状.
x
y
O
1
4
解: 当1
当x>4 , 或x<1时, f'(x)<0可知f(x)在此区间内单调递减;
当x=4 , 或x=1时, f'(x)=0
综上, 函数f(x)图象的大致
形状如右图所示.
三、例题讲解
例2、判断下列函数的单调性, 并求出单调区间:
解:
(1) 因为f(x)=x3+3x, 所以f'(x)=3x2+3=3(x2+1)>0.
因此, 函数f(x)=x3+3x在x∈R上单调递增.
(2) 因为f(x)=x2-2x-3, 所以f'(x)=2x-2=(2x-1).
当f'(x)>0,即x>1时,函数f(x)=x2-2x-3单调递增;
当f'(x)<0,即x<1时,函数f(x)=x2-2x-3单调递减.
解:
例2、判断下列函数的单调性, 并求出单调区间:
2°求可导函数f(x)单调区间的步骤:
①求定义域
②求f'(x)
③令f'(x)>0解不等式?f(x)的递增区间
f'(x)<0解不等式?f(x)的递减区间
④求单调区间
归纳:
1°什么情况下,用“导数法” 求函数单调性、单调区间较简便?
总结: 当遇到三次或三次以上的,或图象很难画出的函数求单调性问题时,应考虑导数法。
例3、已知函数 ,试讨论出此函数的单调区间.并作出图像
四、课堂练习
1、判断下列函数的单调性, 并求出单调区间:
注: 如果一个函数具有相同单调性的单调区间不止一个,这些单调区间一般不能用“∪”连接,而只能用“逗号”或“和”分开。
2、证明函数f(x)=2x3-6x2+7在(0,2)内是减函数
证明:∵f(x)=2x3-6x2+7,∴f'(x)=6x2-12x
由f'(x)<0,解得0
即函数f(x)在(0,2)内是减函数.
注:证明可导函数f(x)在(a,b)内的单调性的方法:
(1)求f'(x)
(2)确认f'(x)在(a,b)内的符号
(3)作出结论
2、证明函数f(x)=2x3-6x2+7在(0,2)内是减函数
3、若在区间(a,b)内有f'(x)>0,且f(a)≥0,则在(a,b)内有( )
A.f(x)>0 B.f(x)<0 C.f(x)=0 D.不能确定
4、函数f(x)=-2x+lnx的增区间是_______,减区间是______
5、已知f(x)=x2+2xf'(1),则f'(1)等于_______
6、求下列函数的单调区间
A
-2
7、确定下列函数的单调区间:
注意到函数的定义域是(-1,+∞),故f(x)的递增区间是(1,+∞);
由f'(x)<0解得-1
