1.3.1函数的单调性与导数2-2020-2021学年人教A版高中数学选修2-2课件(18张PPT)
文档属性
| 名称 | 1.3.1函数的单调性与导数2-2020-2021学年人教A版高中数学选修2-2课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 801.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 21:39:12 | ||
图片预览





文档简介
1.3.1函数的单调性与导数
1、用函数的导数判断函数单调性的法则:
①如果在区间(a,b)内,f'(x)>0,则f(x)在此区间是增函数,(a,b)为f(x)的单调增区间;
②如果在区间(a,b)内,f'(x)<0,则f(x)在此区间是减函数,(a,b)为f(x)的单调减区间;
一、复习回顾
2、求可导函数f(x)单调区间的步骤:
①求定义域
②求f'(x)
③令f'(x)>0解不等式?f(x)的递增区间
f'(x)<0解不等式?f(x)的递减区间
④求单调区间
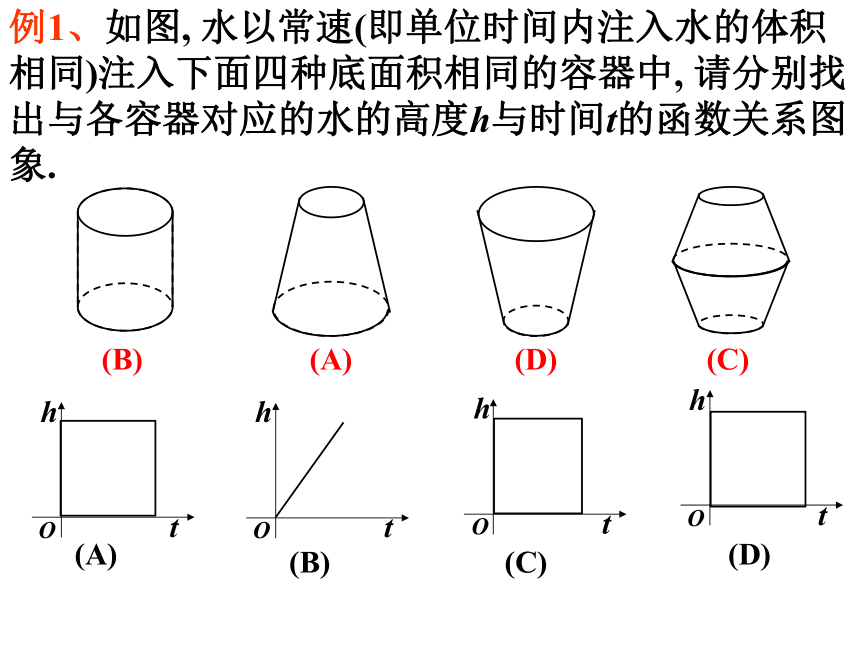
例1、如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.
(A)
(B)
(C)
(D)
h
t
O
h
t
O
h
t
O
h
t
O
(B)
(A)
(D)
(C)
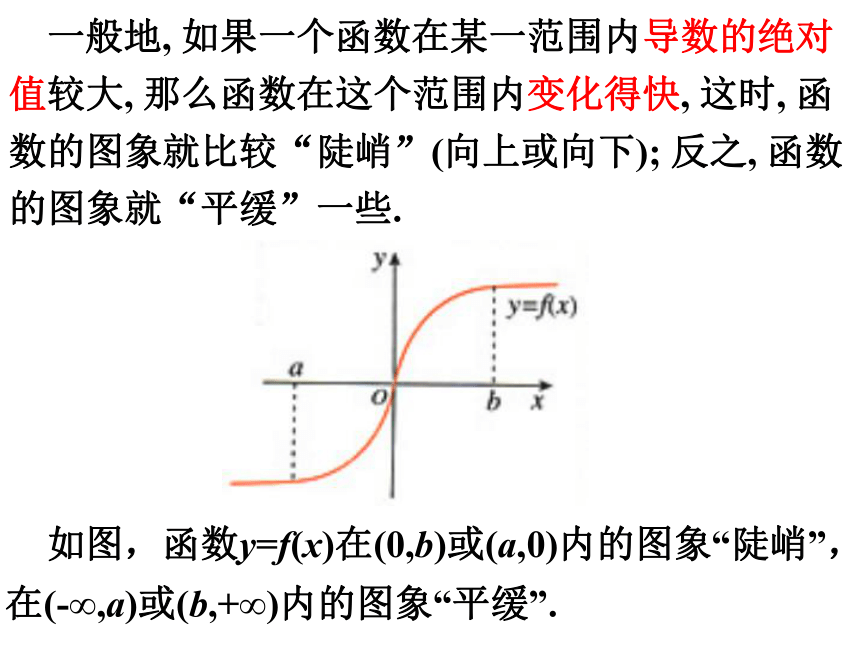
一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些.
如图,函数y=f(x)在(0,b)或(a,0)内的图象“陡峭”,
在(-∞,a)或(b,+∞)内的图象“平缓”.
3、导数与单调性的关系:
对于能否取到等号的问题需要单独验证
f'(x)>0?f(x)在区间(a,b)上是增函数;
f'(x)<0?f(x)在区间(a,b)上是减函数;
反之,
若f(x)在区间(a,b)上是增函数,则f'(x)≥0;
若f(x)在区间(a,b)上是减函数,则f'(x)≤0;
二、求参数的取值范围
例2、若函数f(x)=ax3-x2+x-5在(-∞,+∞)上单调递增,求a的取值范围
练习、已知函数f(x)=2x3-3(1+a)x2+6ax,求函数f(x)的单调区间.
在某个区间上f'(x)>0(或<0)?f(x)单调递增(递减);
但由f(x)在这个区间上单调递增(递减)而仅仅得到f'(x)>0(或<0)是不够的。还有可能导数等于0也能使f(x)在这个区间上单调,因此在已知f(x)在这个区间上单调递增(递减)时;应令f'(x)≥0(或≤0)恒成立,解出参数的范围。
注:
本题用到一个重要的转化:(恒成立问题)
例4、证明不等式ex≥1+x.(x ≥ 0)
提示:构造函数f(x)=ex-1-x,利用导数证明函数f(x)=ex-1-x是增函数,∴ex≥1+x.
三、证明不等式
三、课堂练习
1、已知函数f(x)=2ax-x3,x∈(0,1],a>0,若f(x)在(0,1]上是增函数,求a的取值范围
x
y
o
B
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
C
4、设f'(x)是函数f(x)的导函数,y=f'(x)的图象如右图所示,则y=f(x)的图象最有可能的是( )
5、设函数f(x)=xekx (k≠0)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调区间.
6、已知函数f(x)=x3+ax2+x+1,
(1)当a=2时,求函数f(x)的单调区间;
(2)设函数f(x)在区间 内是减函数,求a的取值范围.
解:(1)当a=2时,f(x)=x3+2x2+x+1,f′(x)=3x2+4x+1,
令f′(x)>0,解得:
令f′(x)<0,解得:
1、已知函数 f(x)=ax?+3x?-x+1 在R上是减函数,求a的取值范围。
a≤-3
四、课外练习
2、已知函数 f(x)=ax-lnx,x∈(0,1],若f(x)在(0,1]上是增函数,求a的取值范围。
[-1,+∞)
1、用函数的导数判断函数单调性的法则:
①如果在区间(a,b)内,f'(x)>0,则f(x)在此区间是增函数,(a,b)为f(x)的单调增区间;
②如果在区间(a,b)内,f'(x)<0,则f(x)在此区间是减函数,(a,b)为f(x)的单调减区间;
一、复习回顾
2、求可导函数f(x)单调区间的步骤:
①求定义域
②求f'(x)
③令f'(x)>0解不等式?f(x)的递增区间
f'(x)<0解不等式?f(x)的递减区间
④求单调区间
例1、如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.
(A)
(B)
(C)
(D)
h
t
O
h
t
O
h
t
O
h
t
O
(B)
(A)
(D)
(C)
一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些.
如图,函数y=f(x)在(0,b)或(a,0)内的图象“陡峭”,
在(-∞,a)或(b,+∞)内的图象“平缓”.
3、导数与单调性的关系:
对于能否取到等号的问题需要单独验证
f'(x)>0?f(x)在区间(a,b)上是增函数;
f'(x)<0?f(x)在区间(a,b)上是减函数;
反之,
若f(x)在区间(a,b)上是增函数,则f'(x)≥0;
若f(x)在区间(a,b)上是减函数,则f'(x)≤0;
二、求参数的取值范围
例2、若函数f(x)=ax3-x2+x-5在(-∞,+∞)上单调递增,求a的取值范围
练习、已知函数f(x)=2x3-3(1+a)x2+6ax,求函数f(x)的单调区间.
在某个区间上f'(x)>0(或<0)?f(x)单调递增(递减);
但由f(x)在这个区间上单调递增(递减)而仅仅得到f'(x)>0(或<0)是不够的。还有可能导数等于0也能使f(x)在这个区间上单调,因此在已知f(x)在这个区间上单调递增(递减)时;应令f'(x)≥0(或≤0)恒成立,解出参数的范围。
注:
本题用到一个重要的转化:(恒成立问题)
例4、证明不等式ex≥1+x.(x ≥ 0)
提示:构造函数f(x)=ex-1-x,利用导数证明函数f(x)=ex-1-x是增函数,∴ex≥1+x.
三、证明不等式
三、课堂练习
1、已知函数f(x)=2ax-x3,x∈(0,1],a>0,若f(x)在(0,1]上是增函数,求a的取值范围
x
y
o
B
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
1
2
x
y
o
2
(A)
(B)
(C)
(D)
C
4、设f'(x)是函数f(x)的导函数,y=f'(x)的图象如右图所示,则y=f(x)的图象最有可能的是( )
5、设函数f(x)=xekx (k≠0)
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调区间.
6、已知函数f(x)=x3+ax2+x+1,
(1)当a=2时,求函数f(x)的单调区间;
(2)设函数f(x)在区间 内是减函数,求a的取值范围.
解:(1)当a=2时,f(x)=x3+2x2+x+1,f′(x)=3x2+4x+1,
令f′(x)>0,解得:
令f′(x)<0,解得:
1、已知函数 f(x)=ax?+3x?-x+1 在R上是减函数,求a的取值范围。
a≤-3
四、课外练习
2、已知函数 f(x)=ax-lnx,x∈(0,1],若f(x)在(0,1]上是增函数,求a的取值范围。
[-1,+∞)
