六年级数学下册课件-7.2.6立体图形的表面积和体积 - 苏教版(共32张PPT)
文档属性
| 名称 | 六年级数学下册课件-7.2.6立体图形的表面积和体积 - 苏教版(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 21.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 09:44:16 | ||
图片预览






文档简介
立体图形的表面积和体积
义务教育教科书小学数学六年级下册
你看到了哪些形体?
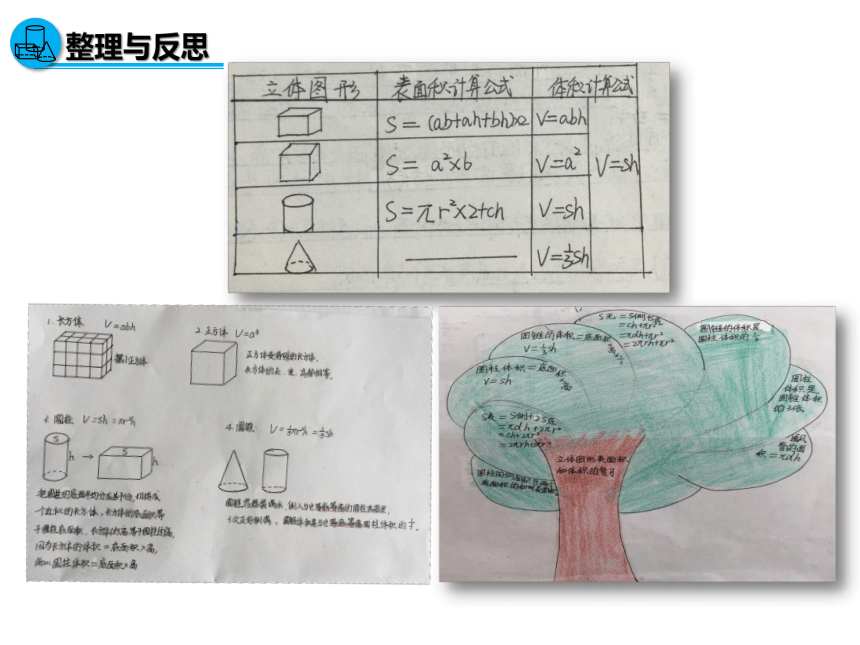
整理与反思
整理与反思
整理与反思
整理与反思
整理与反思
整理与反思
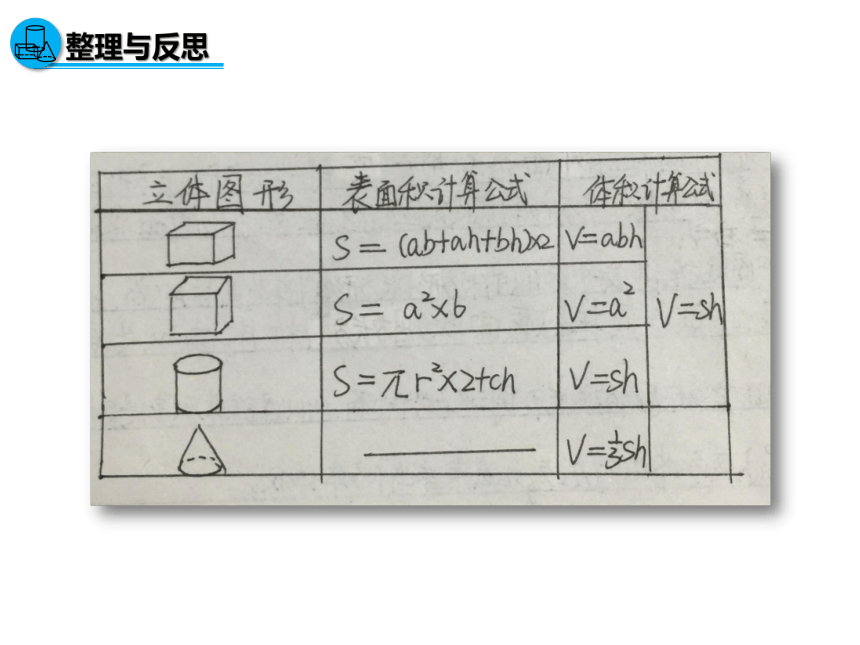
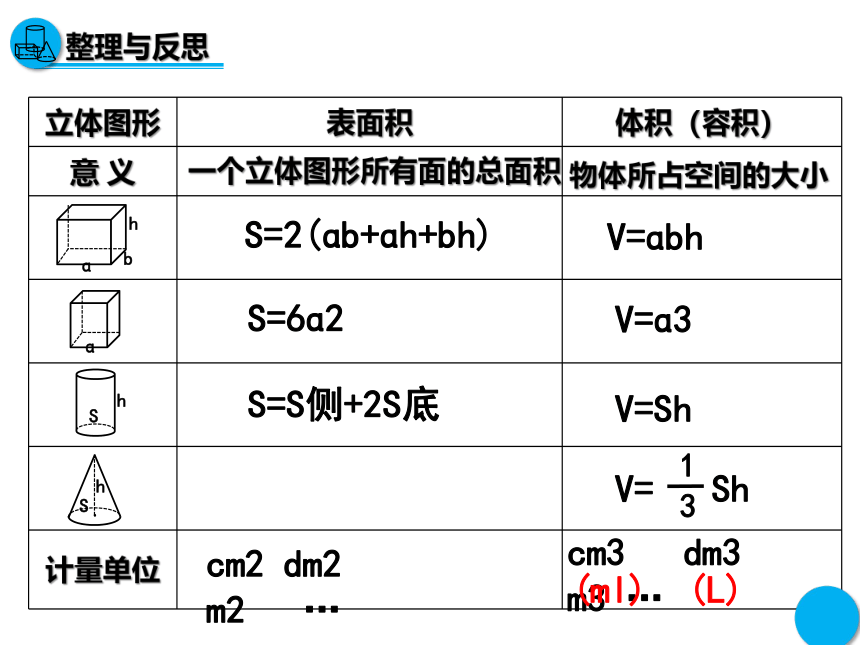
{5940675A-B579-460E-94D1-54222C63F5DA}立体图形
表面积
体积(容积)
意 义
计量单位
ɑ
b
h
ɑ
S
h
S
h
一个立体图形所有面的总面积
物体所占空间的大小
S=2(ɑb+ɑh+bh)
S=S侧+2S底
V=ɑbh
V=ɑ3
V=Sh
cm3 dm3 m3 …
S=6ɑ2
V= Sh
1
3
cm2 dm2 m2 …
(ml) (L)
底面周长
高
圆柱的侧面沿高剪开
S侧=Ch
S侧=πdh
S侧=2πrh
整理与反思
小组活动:
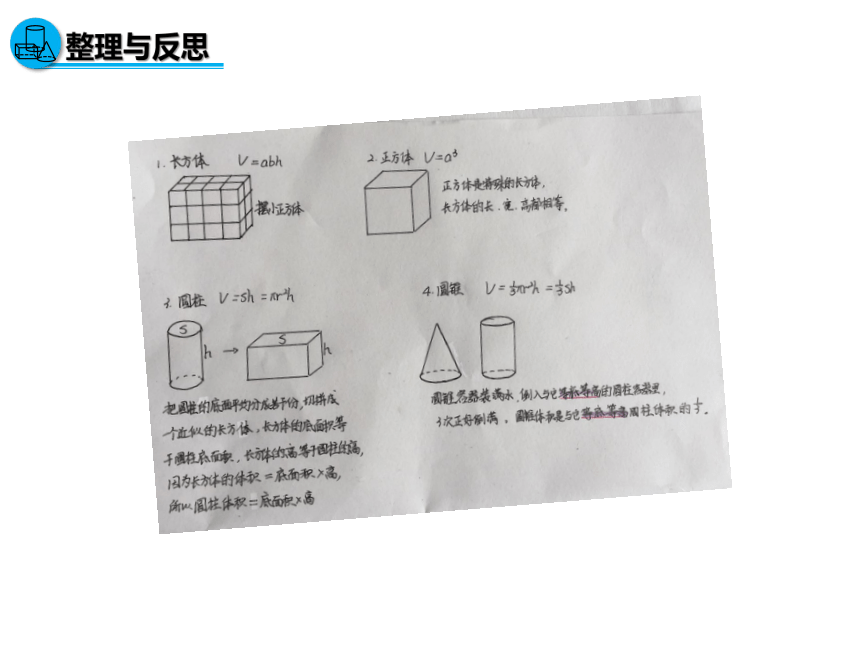
1.说一说:这些立体图形体积公式的推导过程。
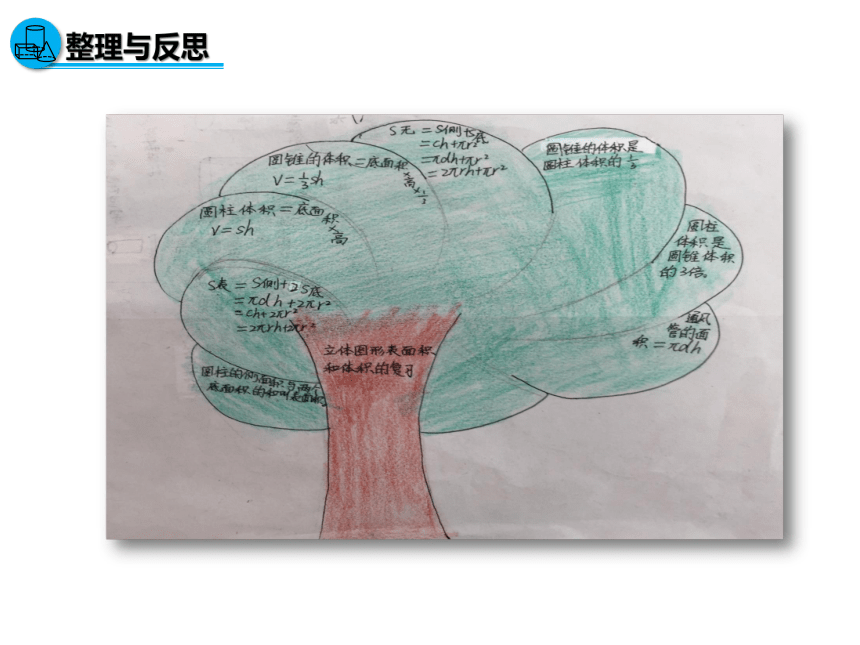
2.想一想:这些体积公式可以怎样分类?
它们之间有怎样的联系?
整理与反思
V=ɑbh
V=ɑ3
V=Sh
V= Sh
1
3
V=Sh
ɑ
b
h
长方体的体积=长×宽×高
V = ɑbh
整理与反思
正方体的体积=棱长×棱长×棱长
V = ɑ×ɑ×ɑ
V = ɑ3
正方体是特殊的长方体,正方体的长、宽、高都相等。
ɑ
整理与反思
整理与反思
把圆柱的底面平均分成若干份,切拼成一个近似的长方体。
S
S
h
h
圆柱的体积=底面积×高
V = Sh
整理与反思
等底等高的圆柱和圆锥形状的空容器各一个。
等底
等高
圆锥的体积 = 底面积 × 高××
V= Sh
1
3
圆锥的体积是与它等底等高的圆柱体积的 。
直柱体
整理与反思
整理与反思
……
V=Sh
整理与反思
练习与实践
π×8×12+2π×(8÷2)?
×3.14×(8÷2)2×12
1.计算这个圆柱的表面积。(单位:厘米)
只列式,不计算。
2. 计算这个圆锥的体积。(单位:厘米)
8
8
练习与实践
3.一个棱长是6分米的正方体,它的表面积和 体积各是多少?
表面积:6×6×6
体积:6×6×6
只列式,不计算。
(1)表示的意义不同
(2)计量的单位不同
(3)计算的方法不同
立体图形的表面积和体积有什么区别?
练习与实践
商标纸的面积有多大?
底面周长22厘米
高20厘米
底面周长60厘米
高25厘米
棱长20厘米
侧面积=底面周长×高
22×20=440(cm2)
60×25=1500(cm2)
20×4×20=1600(cm2)
侧面积=底面周长×高
表面积=侧面积+底面积×2
练习与实践
练习与实践
看了下面的物体,你想求什么?
12.56cm
项目化研究:
侧面展开是正方形
15m
4m
长50m,宽20m,高2m,水高1.5m
每平方米收5千克蔬菜,每千克售3.6元。
活动要求:每组选定一个物体进行研究。
1.想一想:我能解决这个物体的什么问题,组长记录。
2.算一算:选择合适的条件列式解决问题,组长搜集。
3.说一说:在小组里说一说自己的想法。
练习与实践
棱长2分米
你想怎样加工这根木头?
练习与实践
π×(2÷2)2 ×2÷ 23
=6.28÷8
=78.5%
把一个正方体的木头削成一个最大的圆柱,这根木头的利用率是百分之几?
棱长2分米
练习与实践
直径2分米,高2分米
练习与实践
棱长2分米
练习与实践
把一盒优酸乳倒入一个底面积为62平方厘米,高为6厘米的圆锥形水杯中,正好倒满2杯。包装盒上标明的净含量与实际符合吗?
净含量
250ml(±5ml)
245<248<255
答:包装盒上标明的净含量与实际符合。
×62×6×2=248(cm3 )=248(ml)
ɑ
b
h
ɑ
S
h
S
h
整理与反思
义务教育教科书小学数学六年级下册
你看到了哪些形体?
整理与反思
整理与反思
整理与反思
整理与反思
整理与反思
整理与反思
{5940675A-B579-460E-94D1-54222C63F5DA}立体图形
表面积
体积(容积)
意 义
计量单位
ɑ
b
h
ɑ
S
h
S
h
一个立体图形所有面的总面积
物体所占空间的大小
S=2(ɑb+ɑh+bh)
S=S侧+2S底
V=ɑbh
V=ɑ3
V=Sh
cm3 dm3 m3 …
S=6ɑ2
V= Sh
1
3
cm2 dm2 m2 …
(ml) (L)
底面周长
高
圆柱的侧面沿高剪开
S侧=Ch
S侧=πdh
S侧=2πrh
整理与反思
小组活动:
1.说一说:这些立体图形体积公式的推导过程。
2.想一想:这些体积公式可以怎样分类?
它们之间有怎样的联系?
整理与反思
V=ɑbh
V=ɑ3
V=Sh
V= Sh
1
3
V=Sh
ɑ
b
h
长方体的体积=长×宽×高
V = ɑbh
整理与反思
正方体的体积=棱长×棱长×棱长
V = ɑ×ɑ×ɑ
V = ɑ3
正方体是特殊的长方体,正方体的长、宽、高都相等。
ɑ
整理与反思
整理与反思
把圆柱的底面平均分成若干份,切拼成一个近似的长方体。
S
S
h
h
圆柱的体积=底面积×高
V = Sh
整理与反思
等底等高的圆柱和圆锥形状的空容器各一个。
等底
等高
圆锥的体积 = 底面积 × 高××
V= Sh
1
3
圆锥的体积是与它等底等高的圆柱体积的 。
直柱体
整理与反思
整理与反思
……
V=Sh
整理与反思
练习与实践
π×8×12+2π×(8÷2)?
×3.14×(8÷2)2×12
1.计算这个圆柱的表面积。(单位:厘米)
只列式,不计算。
2. 计算这个圆锥的体积。(单位:厘米)
8
8
练习与实践
3.一个棱长是6分米的正方体,它的表面积和 体积各是多少?
表面积:6×6×6
体积:6×6×6
只列式,不计算。
(1)表示的意义不同
(2)计量的单位不同
(3)计算的方法不同
立体图形的表面积和体积有什么区别?
练习与实践
商标纸的面积有多大?
底面周长22厘米
高20厘米
底面周长60厘米
高25厘米
棱长20厘米
侧面积=底面周长×高
22×20=440(cm2)
60×25=1500(cm2)
20×4×20=1600(cm2)
侧面积=底面周长×高
表面积=侧面积+底面积×2
练习与实践
练习与实践
看了下面的物体,你想求什么?
12.56cm
项目化研究:
侧面展开是正方形
15m
4m
长50m,宽20m,高2m,水高1.5m
每平方米收5千克蔬菜,每千克售3.6元。
活动要求:每组选定一个物体进行研究。
1.想一想:我能解决这个物体的什么问题,组长记录。
2.算一算:选择合适的条件列式解决问题,组长搜集。
3.说一说:在小组里说一说自己的想法。
练习与实践
棱长2分米
你想怎样加工这根木头?
练习与实践
π×(2÷2)2 ×2÷ 23
=6.28÷8
=78.5%
把一个正方体的木头削成一个最大的圆柱,这根木头的利用率是百分之几?
棱长2分米
练习与实践
直径2分米,高2分米
练习与实践
棱长2分米
练习与实践
把一盒优酸乳倒入一个底面积为62平方厘米,高为6厘米的圆锥形水杯中,正好倒满2杯。包装盒上标明的净含量与实际符合吗?
净含量
250ml(±5ml)
245<248<255
答:包装盒上标明的净含量与实际符合。
×62×6×2=248(cm3 )=248(ml)
ɑ
b
h
ɑ
S
h
S
h
整理与反思
