六年级数学下册课件-7.2.6立体图形的表面积和体积 苏教版(共30张PPT)
文档属性
| 名称 | 六年级数学下册课件-7.2.6立体图形的表面积和体积 苏教版(共30张PPT) | 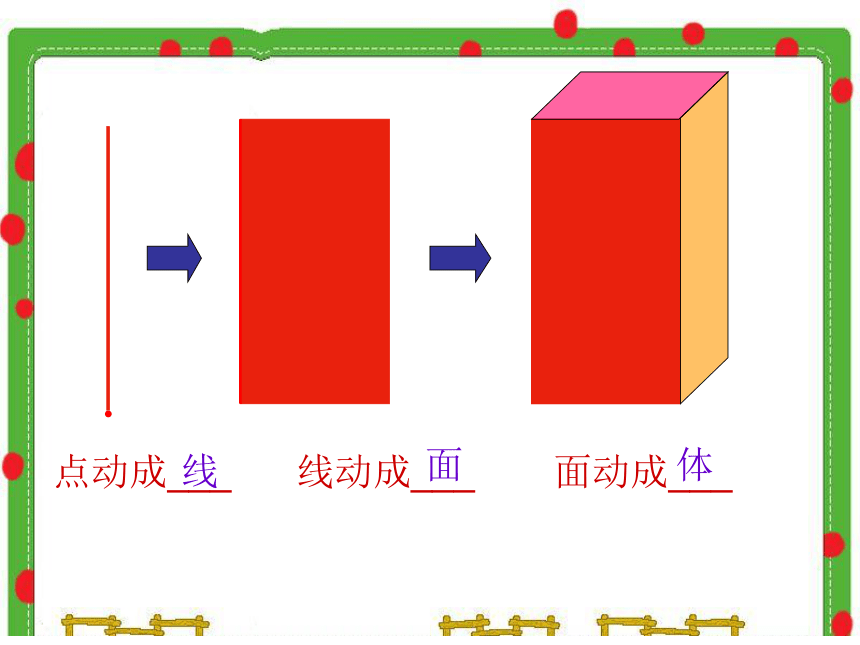 | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 09:45:40 | ||
图片预览







文档简介
(共30张PPT)
点动成___
线
线动成___
面
面动成___
体
立体图形的表面积和体积
(总复习)
一个立体图形所有的面的面积总和,叫做它的表面积.
什么是立体图形的表面积?
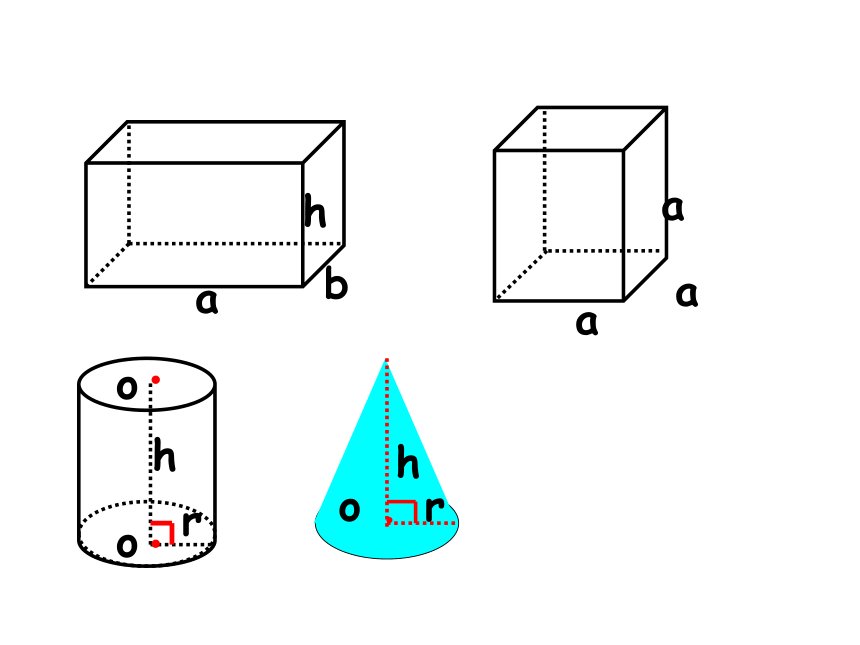
a
h
b
a
a
a
·
h
o
o
r
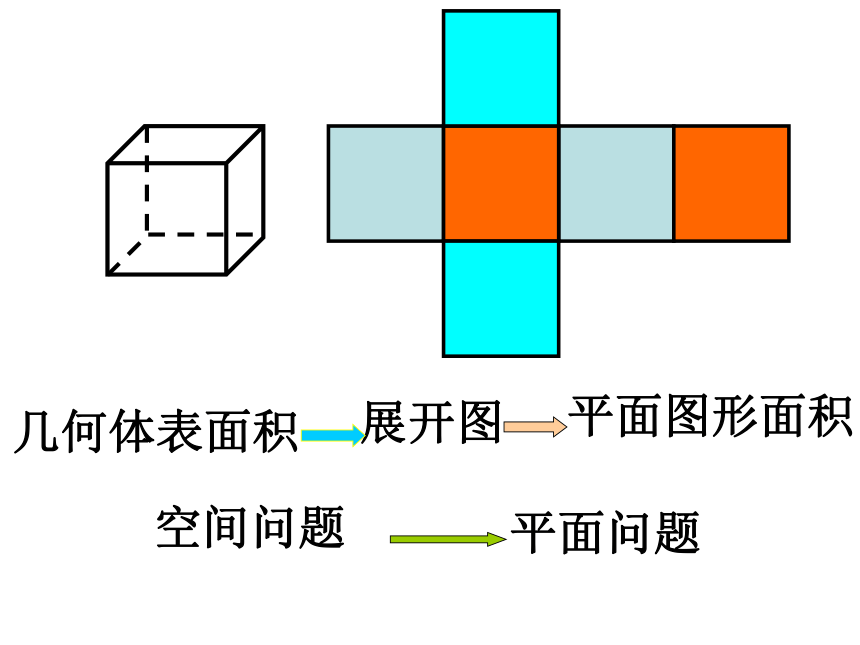
·
展开图
平面图形面积
几何体表面积
空间问题
平面问题
判断下面情况分别求的是什么。
1、油漆柱子的面积
2、长方体的游泳池四周和底面贴瓷砖的面积
游泳池的占地面积
3、制作圆柱形的水桶用铁皮多少
4、电线杆的占地面积
5、计算通风管材料的面积
6、火柴盒的外盒和内盒
一个立体图形所占空间的大小叫做它的体积。
什么是立体图形的体积?
什么是容器的容积?
容器所能容纳的物体的体积叫做它的容积。
a
h
b
a
a
a
·
h
o
o
r
·
h
r
o
·
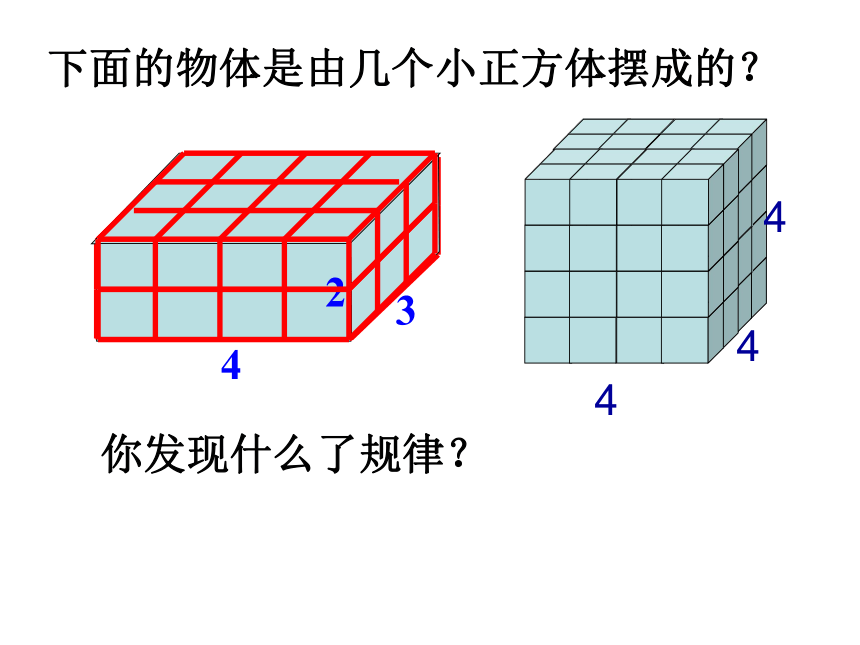
4
2
3
2
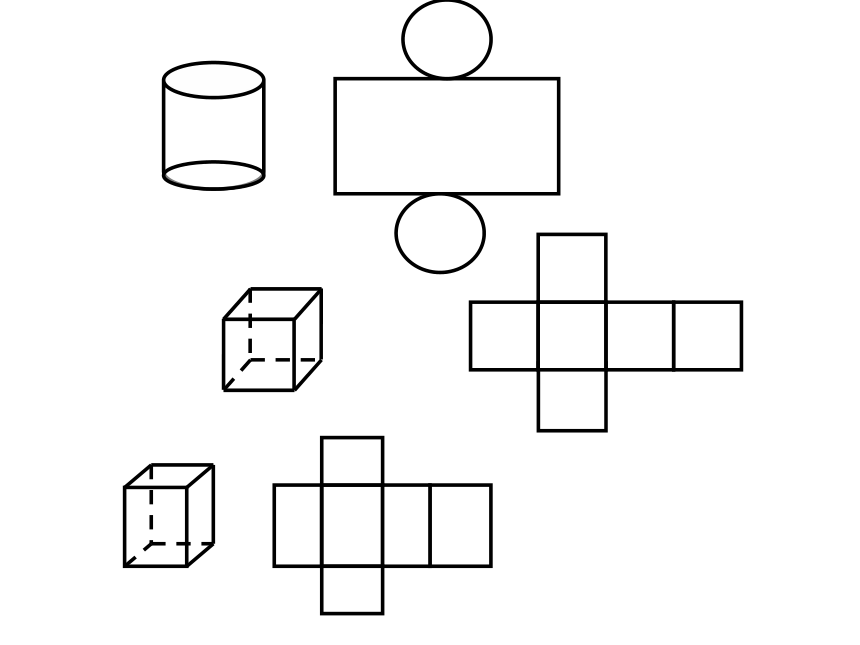
下面的物体是由几个小正方体摆成的?
4
4
4
你发现什么了规律?
长方体所含小正方体的数量正好等于长、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
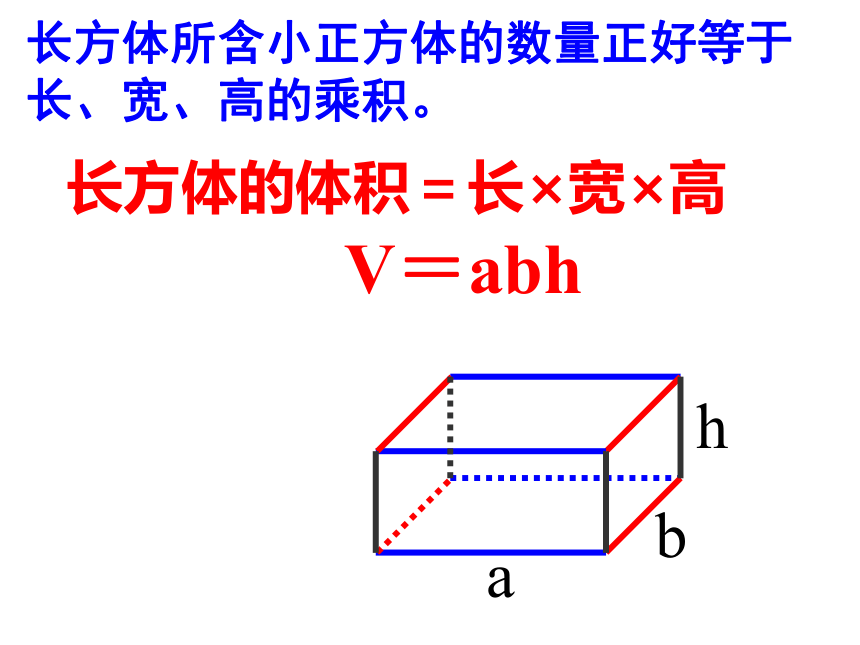
a
b
h
想一想:正方体的体积怎样计算呢?
正方体的体积=棱长×棱长×棱长
V=a.a.a
=a3
a
a
a
你是怎么推导出圆柱的体积公式?
你是怎么推导出圆柱的体积公式?
江苏省电化教育馆制作
圆
柱
长方体
长方体的体积
圆柱的体积
底面积
底面积
高
高
=
×
=
×
拼成的长方体与原来
的圆柱有什么关系?
V
=
S
h
圆锥与它等底等高的圆柱体积关系
圆锥体积是与它等底等高圆柱体积的
1
3
1
3
圆锥的体积=底面积×高
×
1
3
V=
sh
V=abh
V=a
3
V
=
sh
立体图形的表面积和体积的区别
(1)表示的意义不同
(3)计量的单位不同
(2)计算的方法不同
判断题:
1、一个长方体木箱的体积一定大于它的容积。(
)
2、圆锥体体积是圆柱体体积的1/3。(
)
3、圆柱体的侧面积等于底面积乘高。
(
)
4、一个正方体的棱长是6厘米,它的表面积和体积相等。
(
)
5、一个圆柱的底面半径扩大3倍,高缩小3倍,它的体积没变。(
)
√
×
×
×
×
选择正确的答案填在括号里。
1、
一个长方体的长50厘米,宽20分米,高30分米,这个长方体体积的计算方法是(
)
A
、5×20×30
B、
50×2×30
C、
50×20×30
2、
一个圆柱体的底面积是50平方分米,高1米,它的体积是(
)立方分米。
A、
50×1
B
、50×10
C、
5×1
3、一个圆锥体与圆柱体等底等高,圆柱体的体积是60立方米,圆锥体是(
)立方米。
A
、20
B、13
C、6
4、做一个圆柱形的铁皮桶,要用多少铁皮,是求这个铁皮桶的(
),能装多少水是求(
)
A、体积
B、底面积
C、容积
D、表面积
5、把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将
(
)
A、扩大3倍
B、缩小3倍
C、扩大6倍
D、缩小6倍
A
B
A
D
C
A
细心比较
1、一根长方体木料长200厘米,横截面是面积8平方厘米的正方形,这根木料的体积是多少立方厘米?
3、一根长方体木料长200厘米,横截面是周长8厘米的正方形,这根木料的体积是多少立方厘米?
8×200
8×8×200
(8÷4
)2×200
2、一根长方体木料长200厘米,横截面是边长8厘米的正方形,这根木料的体积是多少立方厘米?
1、把一个正方体木块截成两个相同的长方体后,表面积增加了32平方分米,原来正方体的表面积是多少平方分米?
课堂练习:
32÷2×6
2、一个棱长20分米的正方体玻璃容器装满水,然后把水倒入一个长25分米,宽16分米的长方体水箱内,求这时水深多少?
课堂练习:
20×20×20÷(25×16)
4、一根长方体水泥柱,横截面为正方形,边长0.4米,四个侧面的面积之和为4.8平方米,求这根水泥柱的体积是多少立方米?
0.4米
4.8÷4×0.4
0.4米
课堂练习:
把如图所示的三角板以长6厘米的直角边为轴旋转,想象一下,旋转起来的图形是什么形状?你能求出它的体积吗?
4cm
6cm
1
3
V=
sh
π×4?×6×
1
3
4cm
6cm
2、一块长方形铁皮,长5分米,宽3分米,像右图那样从4个角剪掉边长是0.5分米的正方形,然后做成盒子。这个盒子的容积有多少升?
长:5-0.5×2=4(dm)
宽:3-0.5×2=2(dm)
高:0.5dm
V=abh
4×2×0.5
5dm
3dm
0.5dm
4dm
2dm
0.5dm
一个底面边长为10厘米、高为20厘米的长方体容器,将一个土豆放入容器里的水中,水面由5厘米上升到8厘米。这个土豆的体积是多少?
水升高8-5=3cm
8
10×10×3
10
10
20
5
3
把一个圆柱切成若干等分,拼成一个近似的长方体。圆柱的侧面积是72平方米,底面半径是3米。求圆柱的体积是多少?
72÷2×3
圆柱的体积=侧面积÷2×半径
底面积
×
高
解决立体图形实际问题时应该注意什么?
一:要认真读题,看清题要求。(看清什么图形,求什么?如果是求面积要看清求几个面?)
二:要注意统一单位。(看清已知条件单位和求问题的单位是否统一?)
三:用准计算公式(体积、表面积、底面积的公式要选用正确。圆锥体的体积不要忘记乘1/3(除以3))
四:仔细计算,力求每步计算正确。
五:正确写答句。
点动成___
线
线动成___
面
面动成___
体
立体图形的表面积和体积
(总复习)
一个立体图形所有的面的面积总和,叫做它的表面积.
什么是立体图形的表面积?
a
h
b
a
a
a
·
h
o
o
r
·
展开图
平面图形面积
几何体表面积
空间问题
平面问题
判断下面情况分别求的是什么。
1、油漆柱子的面积
2、长方体的游泳池四周和底面贴瓷砖的面积
游泳池的占地面积
3、制作圆柱形的水桶用铁皮多少
4、电线杆的占地面积
5、计算通风管材料的面积
6、火柴盒的外盒和内盒
一个立体图形所占空间的大小叫做它的体积。
什么是立体图形的体积?
什么是容器的容积?
容器所能容纳的物体的体积叫做它的容积。
a
h
b
a
a
a
·
h
o
o
r
·
h
r
o
·
4
2
3
2
下面的物体是由几个小正方体摆成的?
4
4
4
你发现什么了规律?
长方体所含小正方体的数量正好等于长、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
a
b
h
想一想:正方体的体积怎样计算呢?
正方体的体积=棱长×棱长×棱长
V=a.a.a
=a3
a
a
a
你是怎么推导出圆柱的体积公式?
你是怎么推导出圆柱的体积公式?
江苏省电化教育馆制作
圆
柱
长方体
长方体的体积
圆柱的体积
底面积
底面积
高
高
=
×
=
×
拼成的长方体与原来
的圆柱有什么关系?
V
=
S
h
圆锥与它等底等高的圆柱体积关系
圆锥体积是与它等底等高圆柱体积的
1
3
1
3
圆锥的体积=底面积×高
×
1
3
V=
sh
V=abh
V=a
3
V
=
sh
立体图形的表面积和体积的区别
(1)表示的意义不同
(3)计量的单位不同
(2)计算的方法不同
判断题:
1、一个长方体木箱的体积一定大于它的容积。(
)
2、圆锥体体积是圆柱体体积的1/3。(
)
3、圆柱体的侧面积等于底面积乘高。
(
)
4、一个正方体的棱长是6厘米,它的表面积和体积相等。
(
)
5、一个圆柱的底面半径扩大3倍,高缩小3倍,它的体积没变。(
)
√
×
×
×
×
选择正确的答案填在括号里。
1、
一个长方体的长50厘米,宽20分米,高30分米,这个长方体体积的计算方法是(
)
A
、5×20×30
B、
50×2×30
C、
50×20×30
2、
一个圆柱体的底面积是50平方分米,高1米,它的体积是(
)立方分米。
A、
50×1
B
、50×10
C、
5×1
3、一个圆锥体与圆柱体等底等高,圆柱体的体积是60立方米,圆锥体是(
)立方米。
A
、20
B、13
C、6
4、做一个圆柱形的铁皮桶,要用多少铁皮,是求这个铁皮桶的(
),能装多少水是求(
)
A、体积
B、底面积
C、容积
D、表面积
5、把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将
(
)
A、扩大3倍
B、缩小3倍
C、扩大6倍
D、缩小6倍
A
B
A
D
C
A
细心比较
1、一根长方体木料长200厘米,横截面是面积8平方厘米的正方形,这根木料的体积是多少立方厘米?
3、一根长方体木料长200厘米,横截面是周长8厘米的正方形,这根木料的体积是多少立方厘米?
8×200
8×8×200
(8÷4
)2×200
2、一根长方体木料长200厘米,横截面是边长8厘米的正方形,这根木料的体积是多少立方厘米?
1、把一个正方体木块截成两个相同的长方体后,表面积增加了32平方分米,原来正方体的表面积是多少平方分米?
课堂练习:
32÷2×6
2、一个棱长20分米的正方体玻璃容器装满水,然后把水倒入一个长25分米,宽16分米的长方体水箱内,求这时水深多少?
课堂练习:
20×20×20÷(25×16)
4、一根长方体水泥柱,横截面为正方形,边长0.4米,四个侧面的面积之和为4.8平方米,求这根水泥柱的体积是多少立方米?
0.4米
4.8÷4×0.4
0.4米
课堂练习:
把如图所示的三角板以长6厘米的直角边为轴旋转,想象一下,旋转起来的图形是什么形状?你能求出它的体积吗?
4cm
6cm
1
3
V=
sh
π×4?×6×
1
3
4cm
6cm
2、一块长方形铁皮,长5分米,宽3分米,像右图那样从4个角剪掉边长是0.5分米的正方形,然后做成盒子。这个盒子的容积有多少升?
长:5-0.5×2=4(dm)
宽:3-0.5×2=2(dm)
高:0.5dm
V=abh
4×2×0.5
5dm
3dm
0.5dm
4dm
2dm
0.5dm
一个底面边长为10厘米、高为20厘米的长方体容器,将一个土豆放入容器里的水中,水面由5厘米上升到8厘米。这个土豆的体积是多少?
水升高8-5=3cm
8
10×10×3
10
10
20
5
3
把一个圆柱切成若干等分,拼成一个近似的长方体。圆柱的侧面积是72平方米,底面半径是3米。求圆柱的体积是多少?
72÷2×3
圆柱的体积=侧面积÷2×半径
底面积
×
高
解决立体图形实际问题时应该注意什么?
一:要认真读题,看清题要求。(看清什么图形,求什么?如果是求面积要看清求几个面?)
二:要注意统一单位。(看清已知条件单位和求问题的单位是否统一?)
三:用准计算公式(体积、表面积、底面积的公式要选用正确。圆锥体的体积不要忘记乘1/3(除以3))
四:仔细计算,力求每步计算正确。
五:正确写答句。
