六年级数学下册课件 7.2.6立体图形的表面积和体积(共66张ppt) 苏教版
文档属性
| 名称 | 六年级数学下册课件 7.2.6立体图形的表面积和体积(共66张ppt) 苏教版 |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 00:00:00 | ||
图片预览





文档简介
(共66张PPT)
苏教版六年级数学下册
复习提纲:
3、长方体,正方体,圆柱,圆锥的体积计算公
式是什么?
4、这些立体图形体积的计算公式是怎么推导出来的?
它们之间有什么联系?
2、什么是物体的体积?什么是容器的容积?
回忆再现知识
1、什么是长方体、正方体和圆柱的表面积?各怎样计算?
a
b
h
a
a
a
h
r
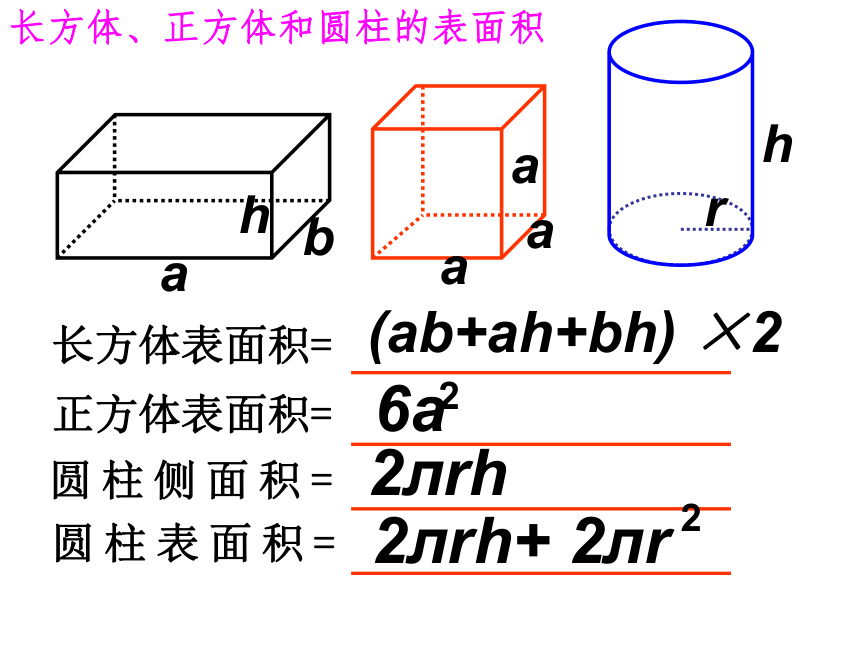
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh)
×2
6a
2лrh
2лrh+
2лr
2
2
长方体、正方体和圆柱的表面积
复习提纲:
3、长方体,正方体,圆柱,圆锥的体积计算公
式是什么?
4、这些立体图形体积的计算公式是怎么推导出来的?
它们之间有什么联系?
2、什么是物体的体积?什么是容器的容积?
回忆再现知识
1、怎样计算长方体、正方体和圆柱的表面积?
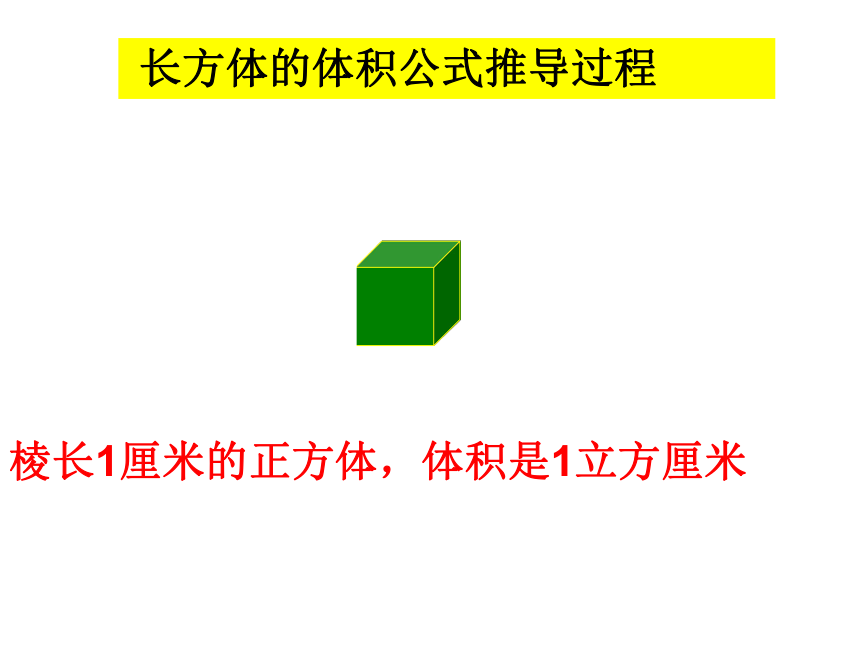
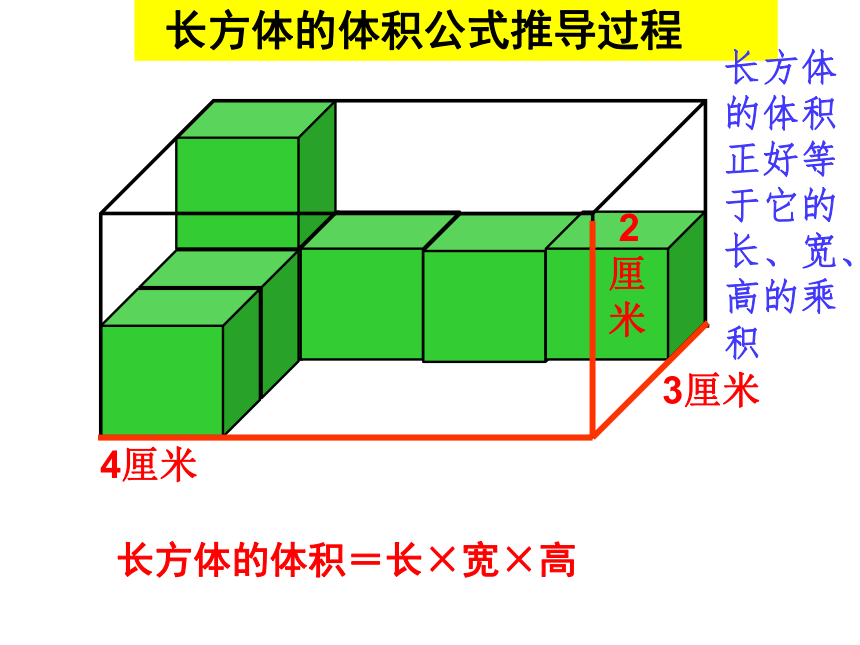
长方体的体积公式推导过程
棱长1厘米的正方体,体积是1立方厘米
4厘米
1厘米
1厘米
3厘米
2厘米
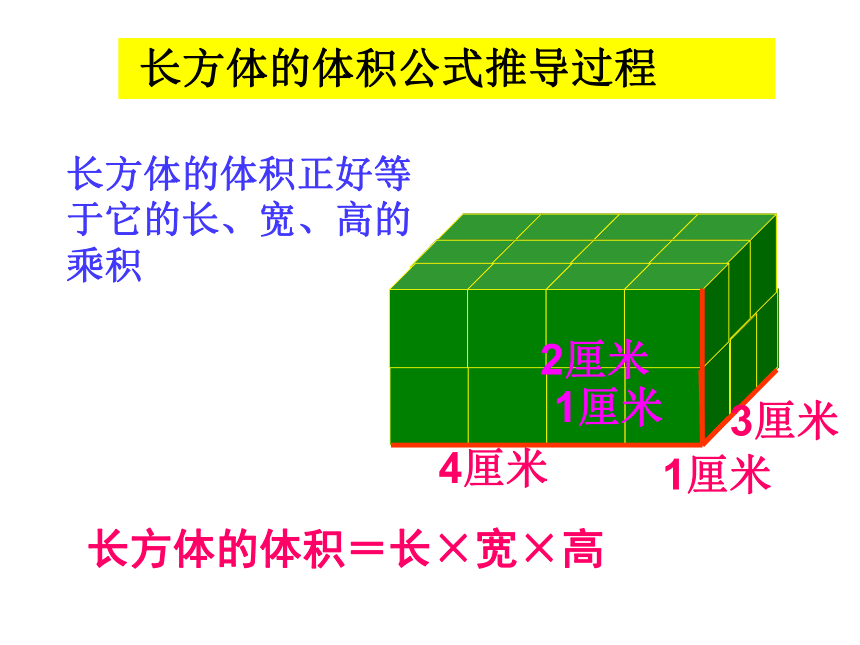
长方体的体积=长×宽×高
长方体的体积公式推导过程
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积公式推导过程
长方体的体积=长×宽×高
4厘米
3厘米
2厘米
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积
=
长
×
宽
×
高
棱长
棱长
棱长
棱长
棱长
棱长
正
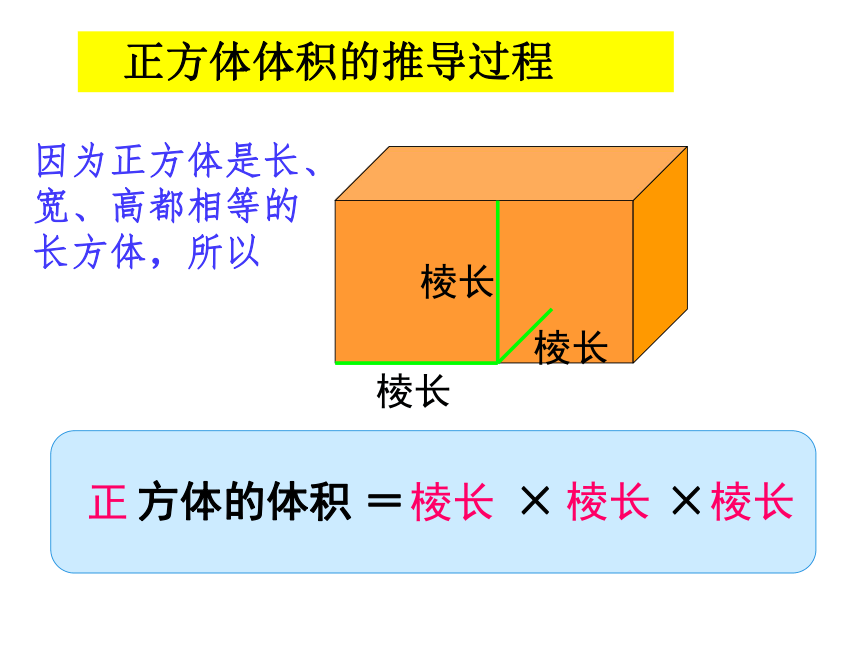
正方体体积的推导过程
因为正方体是长、宽、高都相等的长方体,所以
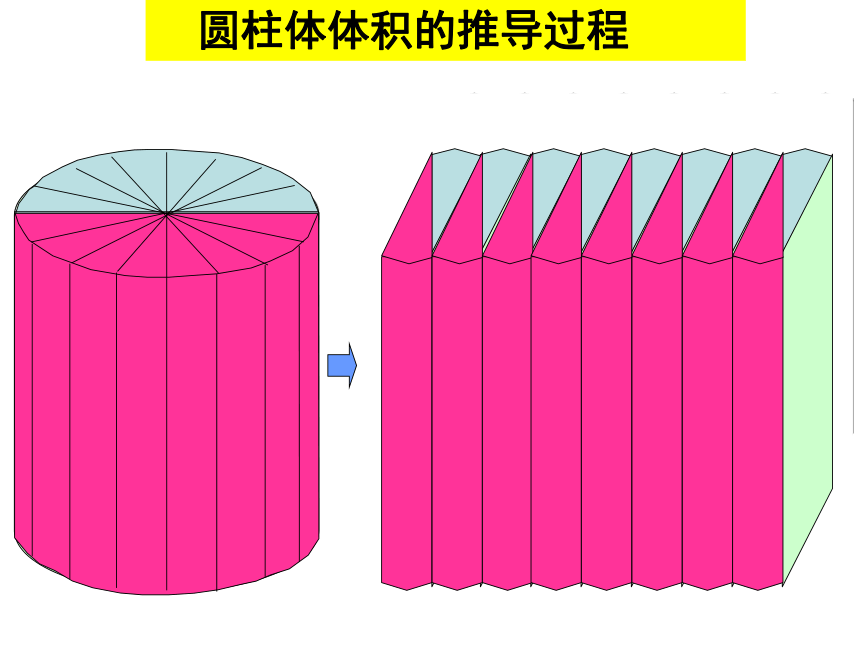
圆柱体体积的推导过程
拼成的长方体与原来的圆柱体比较,什么变了?什么没变?
圆柱体积
长方体体积
底面积
底面积
高
高
=
×
=
×
圆锥体体积的推导过程
结论:圆柱体积是等底等高
圆锥体积的3倍
,圆锥体积是等底等高圆柱体积的
圆锥的体积=
×
底面积
×高
同桌合作,用你喜欢的方法,根据这些立体图形体积的推导之间的联系,动手画一画,试着理出它们的关系图。
理一理,画一画:
梳理整合知识
V
=
sh
a
b
h
a
a
s
h
s
h
V
=
a3
V
=
abh
a
V
=
sh
V
=
sh
1
3
你能推想一下下面的立体图形的体积可以怎样计算吗?
?
1.圆柱说:“我的体积是圆锥的3倍。(
)
2.长方体说:“我和一个圆柱等底面积等高
,我俩的体积相等。”
(
)
×
√
3.油桶说:“我能盛15升水,那么我的体积就是15立方分米.”
(
)
×
4.正方体说:“我的棱长是6分米,我的表面积和体积相等。”
(
)
×
5.圆柱体说:“我的底面半径扩大2倍,高不变,我的体积也扩大4倍。”
(
)
6.一个长方体的长,宽,高分别是a米,b
米,h米。如果高增加2米,体积比原来增加2ab立方米。
(
)
√
√
1、下列立体图形的表面积和体积分别怎样计算?
10
5
4
5
5
5
2
10
(单位:厘米)
(只列式不计算
)
1.一个长方体的鱼池,长10米,宽6米,深是2米。
(1)这个鱼池的占地面积是多少平方米?
10×6=60(平方米)
(2)在这个鱼池的四周和池底铺上瓷砖,瓷砖的面积是多少平方米?
(10×2+6×2)×2+10×6=124(平方米)
(3)在离地面的0.5米处有一道红色的水位线,水位线有多长?
10×2+6×
2=32(米)
(4)鱼池内放满水后能盛放多少立方米的水?
10×6×2=120(立方米)
2.在晒谷场上有一个圆锥形小麦堆,底面周长是12.56米,高1.2米。
(1)这堆小麦的体积是多少立方米?
(2)如果每立方米小麦约重700千克,这堆小麦约重多少吨?(得数保留整数)
把一个圆柱切成若干等分,拼成一个近似的长方体。圆柱的侧面积是72平方米,底面半径是3米。求圆柱的体积是多少?
72÷2×3
圆柱的体积=侧面积÷2×半径
底面积
×
高
四、试一试
苏教版六年级数学下册
复习提纲:
3、长方体,正方体,圆柱,圆锥的体积计算公
式是什么?
4、这些立体图形体积的计算公式是怎么推导出来的?
它们之间有什么联系?
2、什么是物体的体积?什么是容器的容积?
回忆再现知识
1、什么是长方体、正方体和圆柱的表面积?各怎样计算?
a
b
h
a
a
a
h
r
长方体表面积=
正方体表面积=
圆柱侧面积=
圆柱表面积=
(ab+ah+bh)
×2
6a
2лrh
2лrh+
2лr
2
2
长方体、正方体和圆柱的表面积
复习提纲:
3、长方体,正方体,圆柱,圆锥的体积计算公
式是什么?
4、这些立体图形体积的计算公式是怎么推导出来的?
它们之间有什么联系?
2、什么是物体的体积?什么是容器的容积?
回忆再现知识
1、怎样计算长方体、正方体和圆柱的表面积?
长方体的体积公式推导过程
棱长1厘米的正方体,体积是1立方厘米
4厘米
1厘米
1厘米
3厘米
2厘米
长方体的体积=长×宽×高
长方体的体积公式推导过程
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积公式推导过程
长方体的体积=长×宽×高
4厘米
3厘米
2厘米
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积
=
长
×
宽
×
高
棱长
棱长
棱长
棱长
棱长
棱长
正
正方体体积的推导过程
因为正方体是长、宽、高都相等的长方体,所以
圆柱体体积的推导过程
拼成的长方体与原来的圆柱体比较,什么变了?什么没变?
圆柱体积
长方体体积
底面积
底面积
高
高
=
×
=
×
圆锥体体积的推导过程
结论:圆柱体积是等底等高
圆锥体积的3倍
,圆锥体积是等底等高圆柱体积的
圆锥的体积=
×
底面积
×高
同桌合作,用你喜欢的方法,根据这些立体图形体积的推导之间的联系,动手画一画,试着理出它们的关系图。
理一理,画一画:
梳理整合知识
V
=
sh
a
b
h
a
a
s
h
s
h
V
=
a3
V
=
abh
a
V
=
sh
V
=
sh
1
3
你能推想一下下面的立体图形的体积可以怎样计算吗?
?
1.圆柱说:“我的体积是圆锥的3倍。(
)
2.长方体说:“我和一个圆柱等底面积等高
,我俩的体积相等。”
(
)
×
√
3.油桶说:“我能盛15升水,那么我的体积就是15立方分米.”
(
)
×
4.正方体说:“我的棱长是6分米,我的表面积和体积相等。”
(
)
×
5.圆柱体说:“我的底面半径扩大2倍,高不变,我的体积也扩大4倍。”
(
)
6.一个长方体的长,宽,高分别是a米,b
米,h米。如果高增加2米,体积比原来增加2ab立方米。
(
)
√
√
1、下列立体图形的表面积和体积分别怎样计算?
10
5
4
5
5
5
2
10
(单位:厘米)
(只列式不计算
)
1.一个长方体的鱼池,长10米,宽6米,深是2米。
(1)这个鱼池的占地面积是多少平方米?
10×6=60(平方米)
(2)在这个鱼池的四周和池底铺上瓷砖,瓷砖的面积是多少平方米?
(10×2+6×2)×2+10×6=124(平方米)
(3)在离地面的0.5米处有一道红色的水位线,水位线有多长?
10×2+6×
2=32(米)
(4)鱼池内放满水后能盛放多少立方米的水?
10×6×2=120(立方米)
2.在晒谷场上有一个圆锥形小麦堆,底面周长是12.56米,高1.2米。
(1)这堆小麦的体积是多少立方米?
(2)如果每立方米小麦约重700千克,这堆小麦约重多少吨?(得数保留整数)
把一个圆柱切成若干等分,拼成一个近似的长方体。圆柱的侧面积是72平方米,底面半径是3米。求圆柱的体积是多少?
72÷2×3
圆柱的体积=侧面积÷2×半径
底面积
×
高
四、试一试
