六年级数学下册课件-7.2.6立体图形的表面积和体积-苏教版(共68张PPT)
文档属性
| 名称 | 六年级数学下册课件-7.2.6立体图形的表面积和体积-苏教版(共68张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 09:59:33 | ||
图片预览




文档简介
(共68张PPT)
苏教版六年级数学下册总复习
2)理解并掌握各立体图形表面积和体积的计算公式并进行系统地整理。
4)能应用公式进行有关计算,解决生活中的实际问题。
3)理解各立体图形表面积和体积公式的推导过程。
复习目标
1)理解表面积和体积的含义。
表面积:物体表面的总面积叫做物体的表面积。
体
积:物体所占空间的大小叫做物体的体积。
容
积:容器所能容纳物体的体积叫做容器的容积。
1000
1000
1000
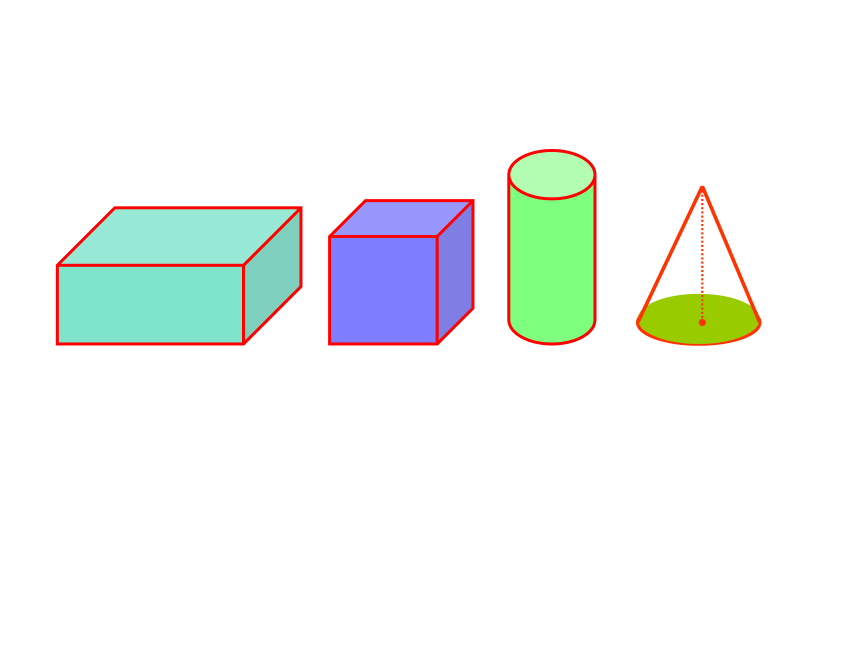
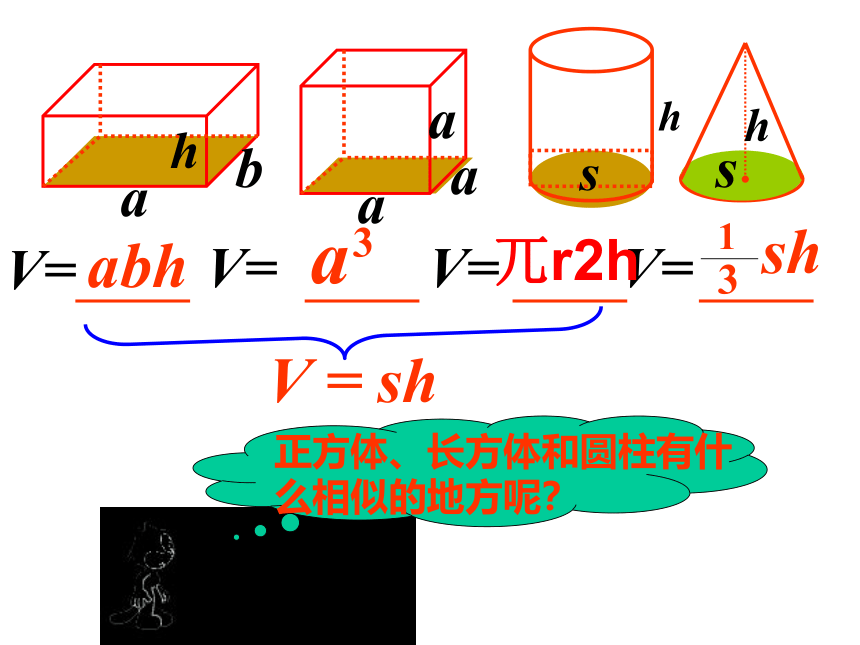
V=
V=
V=
V=
abh
a
3
兀r2h
1
3
sh
V
=
sh
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
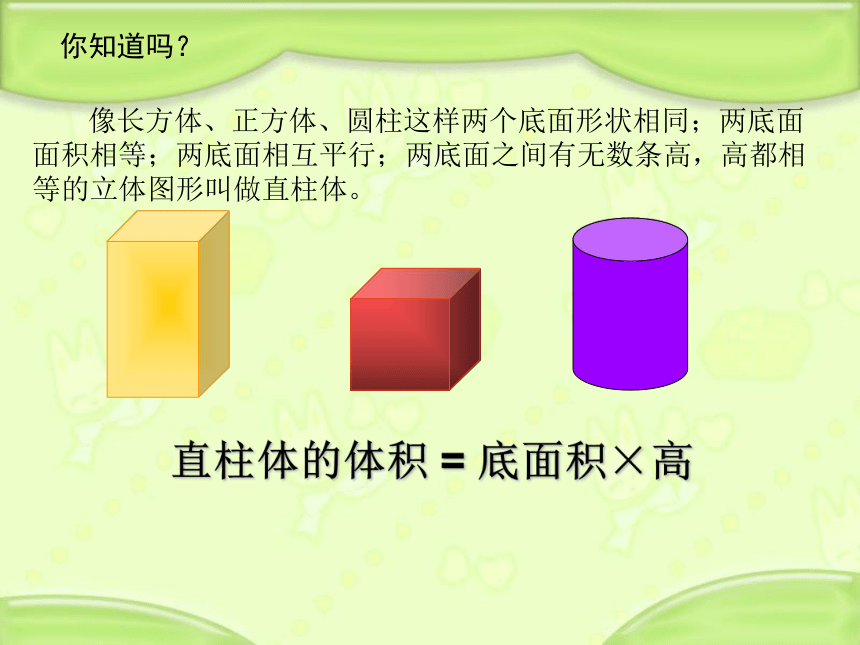
直柱体的体积
=
底面积×高
像长方体、正方体、圆柱这样两个底面形状相同;两底面面积相等;两底面相互平行;两底面之间有无数条高,高都相等的立体图形叫做直柱体。
你知道吗?
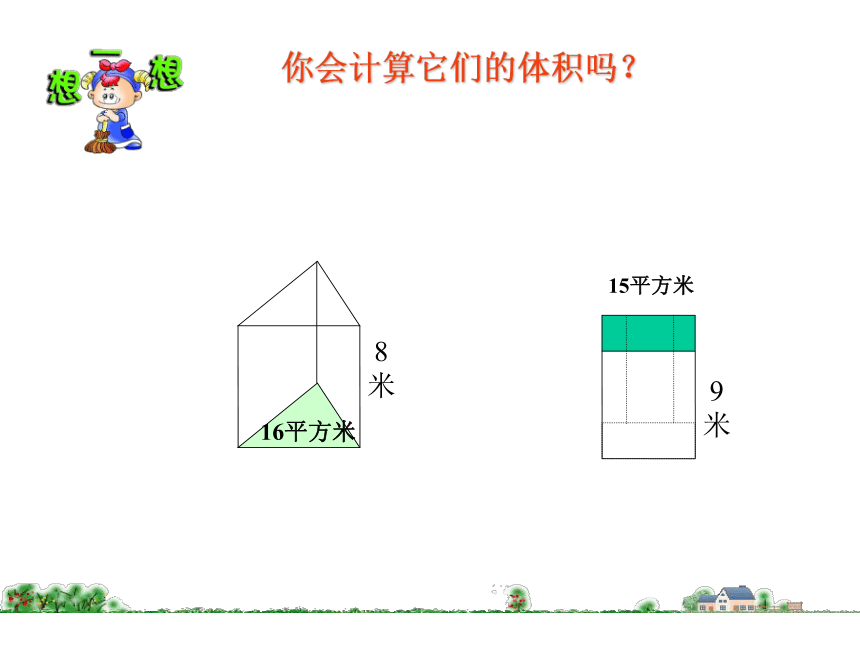
16平方米
8
米
9
米
15平方米
你会计算它们的体积吗?
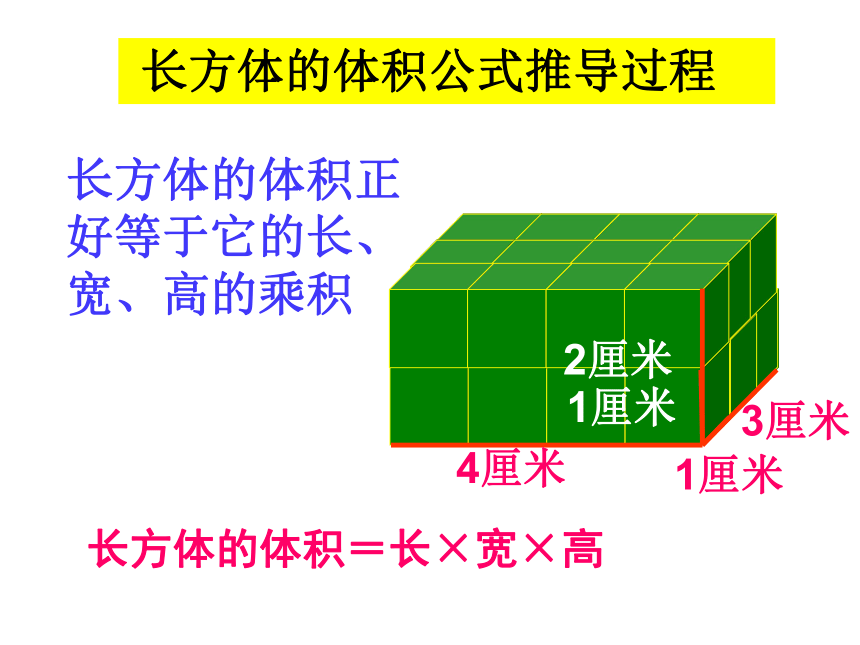
长方体的体积公式推导过程
棱长1厘米的正方体,体积是1立方厘米
4厘米
1厘米
1厘米
3厘米
2厘米
长方体的体积=长×宽×高
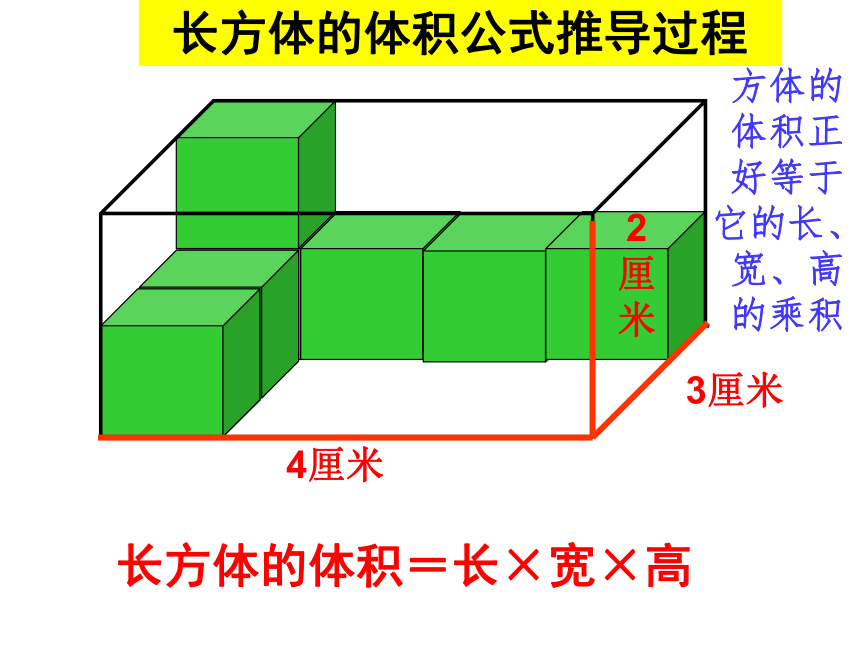
长方体的体积公式推导过程
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积公式推导过程
长方体的体积=长×宽×高
4厘米
3厘米
2厘米
方体的体积正好等于它的长、宽、高的乘积
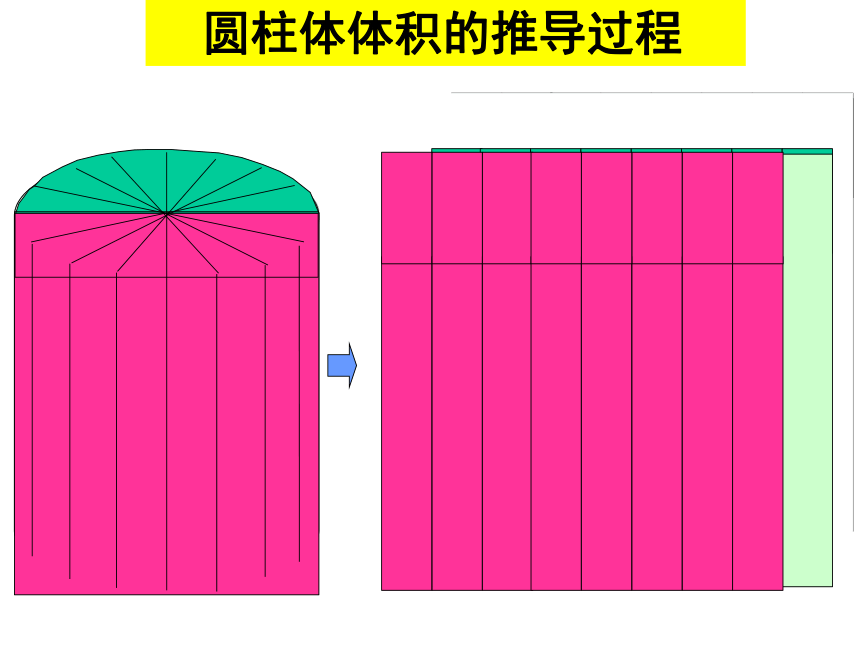
圆柱体体积的推导过程
拼成的长方体与原来的圆柱体比较,什么变了?什么没变?
圆柱体积
长方体体积
底面积
底面积
高
高
=
×
=
×
圆锥体体积的推导过程
结论:圆柱体积是等底等高
圆锥体积的3倍
,圆锥体积是等底等高圆柱体积的
圆锥的体积=
×
底面积
×高
转化
实验、转化
推导体积计算公式
推导体积计算公式
主要利用转化,类比的数学思想方法
小结
练习与实践
1、在括号里填上合适的单位。
(1)一间卧室地面的面积是15(
)。
(2)一瓶牛奶大约有250(
)。
(3)一间教室的空间大约是144(
)。
(4)一台微波炉的体积是92(
),容积是25(
)。
m?
ml
m?
dm?
L
2.单位换算
0.5m?=(
)dm?
4050
dm?
=(
)m?
0.09
dm?
=(
)cm?
60
cm?
=(
)dm?
1.04L
=(
)mL
75
mL
=(
)
cm?
练习与实践
4.05
500
90
0.06
1040
75
0.5×1000
4050÷1000
练习与实践:
3、(举例说明,加深印象)
(1)制作通风管所需材料是求(
).
(2)圆锥形沙堆占地面积指的是(
).
(3)用玻璃做正方体的金鱼缸,最少需多少玻璃是求(
).
(4)压路机前轮向前滚动一周前进了多少米是求(
).
(5)做一个长方体框架需要多少铁丝是求(
)
(6)圆柱形无盖铁皮水桶是求(
).
侧面积
底面积
5个面的面积和
底面周长
棱长总和
侧面积+底面积
练习与实践:
4、求下面立体图形的表面积和体积(只列式不计算)
表面积:
体积:
42×6
43
(5×4+5×3+4×3)×2
5×4×3
3.14×10×5+3.14×(10÷2)2×2
3.14×(10÷2)2×5
1.一个长方体的鱼池,长10米,宽6米,深是2米。
(1)这个鱼池的占地面积是多少平方米?
(2)在这个鱼池的四周和池底铺上瓷砖,瓷砖的面积是多少平方米?
(3)在离地面的0.5米处有一道红色的水位线,水位线有多长?
(4)鱼池内放满水后能盛放多少立方米的水?
1.一个长方体的鱼池,长10米,宽6米,深是2米。
(1)10×6=60(平方米)
(2)(10×2+6×2)×2+10×6=124(平方米)
(3)10×2+6×2=32(米)
(4)10×6×2=120(立方米)
2、一个圆锥形黄沙堆,底面周长18.84米,高2米,把这些沙在5米宽的公路上铺2厘米厚,够铺200米长的路吗?
〔(18.84÷3.14÷2)×3.14×2×
〕÷(5×0.02)
2厘米=0.02米
=18.84÷0.1
=188.4(米)
200米>188.4米
答:不够铺200米长的路。
2
3、王叔叔有一块长方形铁皮,利用图中的阴影部分(如图)正好能做一个油桶。你知道这个油桶的体积有多大吗?(接头处忽略不计)
16.56分米
直径:16.56÷(3.14+1)=4(分米)
体积:3.14×(4÷2)2
×(4×2)
=3.14×4×8
=100.48(立方分米)
怎样测量一块石头的体积
苏教版六年级数学下册总复习
2)理解并掌握各立体图形表面积和体积的计算公式并进行系统地整理。
4)能应用公式进行有关计算,解决生活中的实际问题。
3)理解各立体图形表面积和体积公式的推导过程。
复习目标
1)理解表面积和体积的含义。
表面积:物体表面的总面积叫做物体的表面积。
体
积:物体所占空间的大小叫做物体的体积。
容
积:容器所能容纳物体的体积叫做容器的容积。
1000
1000
1000
V=
V=
V=
V=
abh
a
3
兀r2h
1
3
sh
V
=
sh
正方体、长方体和圆柱有什么相似的地方呢?
h
a
b
a
a
a
s
h
s
h
直柱体的体积
=
底面积×高
像长方体、正方体、圆柱这样两个底面形状相同;两底面面积相等;两底面相互平行;两底面之间有无数条高,高都相等的立体图形叫做直柱体。
你知道吗?
16平方米
8
米
9
米
15平方米
你会计算它们的体积吗?
长方体的体积公式推导过程
棱长1厘米的正方体,体积是1立方厘米
4厘米
1厘米
1厘米
3厘米
2厘米
长方体的体积=长×宽×高
长方体的体积公式推导过程
长方体的体积正好等于它的长、宽、高的乘积
长方体的体积公式推导过程
长方体的体积=长×宽×高
4厘米
3厘米
2厘米
方体的体积正好等于它的长、宽、高的乘积
圆柱体体积的推导过程
拼成的长方体与原来的圆柱体比较,什么变了?什么没变?
圆柱体积
长方体体积
底面积
底面积
高
高
=
×
=
×
圆锥体体积的推导过程
结论:圆柱体积是等底等高
圆锥体积的3倍
,圆锥体积是等底等高圆柱体积的
圆锥的体积=
×
底面积
×高
转化
实验、转化
推导体积计算公式
推导体积计算公式
主要利用转化,类比的数学思想方法
小结
练习与实践
1、在括号里填上合适的单位。
(1)一间卧室地面的面积是15(
)。
(2)一瓶牛奶大约有250(
)。
(3)一间教室的空间大约是144(
)。
(4)一台微波炉的体积是92(
),容积是25(
)。
m?
ml
m?
dm?
L
2.单位换算
0.5m?=(
)dm?
4050
dm?
=(
)m?
0.09
dm?
=(
)cm?
60
cm?
=(
)dm?
1.04L
=(
)mL
75
mL
=(
)
cm?
练习与实践
4.05
500
90
0.06
1040
75
0.5×1000
4050÷1000
练习与实践:
3、(举例说明,加深印象)
(1)制作通风管所需材料是求(
).
(2)圆锥形沙堆占地面积指的是(
).
(3)用玻璃做正方体的金鱼缸,最少需多少玻璃是求(
).
(4)压路机前轮向前滚动一周前进了多少米是求(
).
(5)做一个长方体框架需要多少铁丝是求(
)
(6)圆柱形无盖铁皮水桶是求(
).
侧面积
底面积
5个面的面积和
底面周长
棱长总和
侧面积+底面积
练习与实践:
4、求下面立体图形的表面积和体积(只列式不计算)
表面积:
体积:
42×6
43
(5×4+5×3+4×3)×2
5×4×3
3.14×10×5+3.14×(10÷2)2×2
3.14×(10÷2)2×5
1.一个长方体的鱼池,长10米,宽6米,深是2米。
(1)这个鱼池的占地面积是多少平方米?
(2)在这个鱼池的四周和池底铺上瓷砖,瓷砖的面积是多少平方米?
(3)在离地面的0.5米处有一道红色的水位线,水位线有多长?
(4)鱼池内放满水后能盛放多少立方米的水?
1.一个长方体的鱼池,长10米,宽6米,深是2米。
(1)10×6=60(平方米)
(2)(10×2+6×2)×2+10×6=124(平方米)
(3)10×2+6×2=32(米)
(4)10×6×2=120(立方米)
2、一个圆锥形黄沙堆,底面周长18.84米,高2米,把这些沙在5米宽的公路上铺2厘米厚,够铺200米长的路吗?
〔(18.84÷3.14÷2)×3.14×2×
〕÷(5×0.02)
2厘米=0.02米
=18.84÷0.1
=188.4(米)
200米>188.4米
答:不够铺200米长的路。
2
3、王叔叔有一块长方形铁皮,利用图中的阴影部分(如图)正好能做一个油桶。你知道这个油桶的体积有多大吗?(接头处忽略不计)
16.56分米
直径:16.56÷(3.14+1)=4(分米)
体积:3.14×(4÷2)2
×(4×2)
=3.14×4×8
=100.48(立方分米)
怎样测量一块石头的体积
