2020-2021学年湘教版八年级下册数学期中复习检测卷(Word版,附答案)
文档属性
| 名称 | 2020-2021学年湘教版八年级下册数学期中复习检测卷(Word版,附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 435.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 00:00:00 | ||
图片预览



文档简介
2020-2021学年七年级下册数学期中复习检测卷(湘教版)
选择题(本大题共有8个小题,每小题3分,共24分)
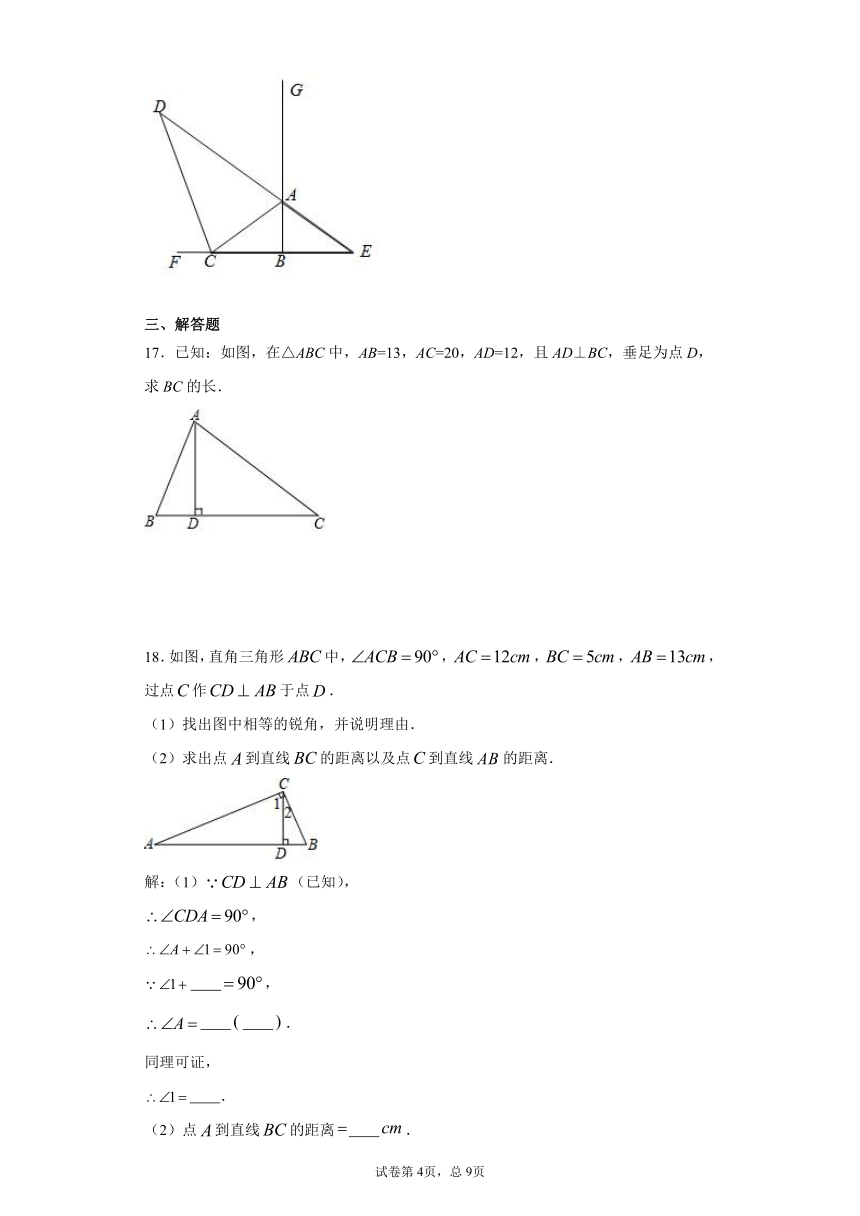
1.下列图案既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
2.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=
CD
3.如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于(
)
A.3.5
B.4
C.7
D.14
4.如图,矩形纸片中,,,将沿折叠,使点落在点处,交于点,则的长等于(
)
A.
B.
C.
D.
5.一个多边形的外角和是内角和的,这个多边形的边数为(
)
A.5
B.6
C.7
D.8
6.如图在中,于,于,为的中点,,的周长为13,则的长是
A.6
B.8
C.10
D.12
7.把一块等腰直角三角尺和直尺如图放置,如果,则的度数为
A.
B.
C.
D.
8.如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
A.2
B.
C.4
D.
填空题(本大题共8个小题,每小题3分,共24分)
9.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长_______.
10.如图,在Rt△BAC和Rt△BDC中,∠BAC=∠BDC=90°,O是BC的中点,连接AO、DO.若AO=3,则DO的长为_____.
11.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,S△BDC=4,BC=8,则AD=_________.
12.如图,将一张直角三角形纸片对折,使点B、C重合,折痕为DE,连接DC,若AC=6cm,∠ACB=90°,∠B=30°,则△ADC的周长是_____cm.
13.如图,在□ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB=
_________cm.
14.已知一个直角三角形斜边上的中线长为6
cm,那么这个直角三角形的斜边长为______cm.
15.如图,在正方形ABCD中,对角线为AC,在BC延长线上取一点F,有AC=CF,AF与DC相交于点E,AB=4,则CF=_____,∠AEC=_____.
16.如图,在中,,,,和分别是其外角和的角平分线,延长和相交于点E,则_____度,_____.
三、解答题
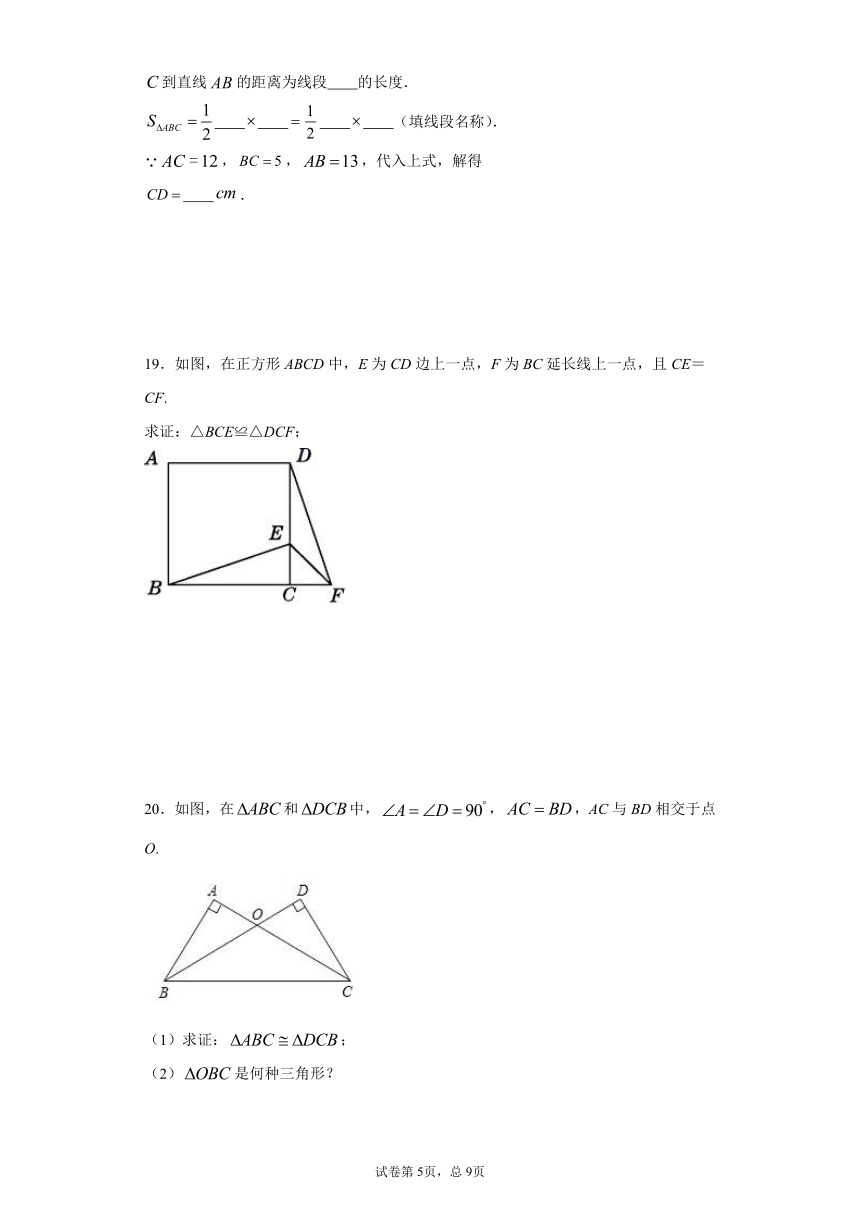
17.已知:如图,在△ABC中,AB=13,AC=20,AD=12,且AD⊥BC,垂足为点D,求BC的长.
18.如图,直角三角形中,,,,,过点作于点.
(1)找出图中相等的锐角,并说明理由.
(2)求出点到直线的距离以及点到直线的距离.
解:(1)(已知),
,
,
,
.
同理可证,
.
(2)点到直线的距离 .
到直线的距离为线段 的长度.
(填线段名称).
,,,代入上式,解得
.
19.如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.
求证:△BCE≌△DCF;
20.如图,在和中,,,AC与BD相交于点O.
(1)求证:;
(2)是何种三角形?
21.如图,在△ABC中,AB,BC,CA的中点分别是点E,F,G,AD是高,连接ED,EF,FG,DG.求证:∠EDG=∠EFG.
22.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
23.将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,
①求菱形的边长;
②求折痕EF的长.
24.已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
25.如图,在中,,是过点的直线,于,于点;
(1)若、在的同侧(如图所示)且.求证:;
(2)若、在的两侧(如图所示),且,其他条件不变,与仍垂直吗?若是请给出证明;若不是,请说明理由.
26.如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(
)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.A
2.D
3.A
4.A
5.C
6.B
7.B
8.C
9.2
10.3
11.1
12.18
13.
14.12
15.
112.5°
16.45°
6
17.21
【解析】
【详解】
∵AB=13,AC=20,AD=12,AD⊥BC,
∴Rt△ABD中,BD===5,
Rt△ACD中,CD===16,
∴BC=BD+CD=5+16=21.
18.(1)
∠2;∠2;同角的余角相等;∠B;
(2)12;CD;AC;BC;AB;CD;.
【详解】
(1)CD⊥AB(已知),
∴∠CDA=90?
∴∠A+∠1=90?,
∵∠1+∠2=90?,
∴∠A=∠2
同角的余角相等).
同理可证,
∴∠1=∠B.
故答案为∠2;∠2;同角的余角相等;∠B;
(2)点A到直线BC的距离=12cm.
C到直线AB的距离为线段CD的长度.
S△ABC=AC×BC=AB×CD.
∵AC=12,BC=5,AB=13,代入上式,解得
CD=cm.
故答案为5;
CD;AC;BC;AB;CD;.
19.证明见解析
【解析】
试题分析:由正方形的性质得出BC=DC,∠BCE=∠DCF=90°,由SAS证明△BCE≌△DCF.
试题解析:
证明:在正方形ABCD中
BC=DC,∠BCE=∠DCF=90°,
在△BCE与△DCF中,
∴△BCE≌△DCF.
20.(1)见解析;(2)△OBC是等腰三角形,理由见解析.
【详解】
(1)∵∠A=∠D=90°,
∴在Rt△ABC和Rt△DCB中,,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
理由:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
21.见解析.
【解析】
证明:连接EG.
∵点E,F分别是AB,BC的中点,∴EF为△ABC的中位线,
∴EF=AC.
又∵AD⊥BC,∴∠ADC=90°,
DG为Rt△ADC斜边上的中线,
∴DG=AC,∴DG=EF
.同理可证DE=FG.
又∵EG=GE,
∴△EFG≌△GDE(SSS),
∴∠EDG=∠EFG.
22.(1)见解析;(2)四边形BECD是菱形,理由见解析;(3)当∠A=45°时,四边形BECD是正方形,理由见解析
【详解】
(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
23.(1)见解析;(2)①5;②2.
【详解】
(1)∵矩形ABCD折叠使A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,
∴∠FAC=∠ECA,在△AOF和△COE中,
∴△AOF≌△COE,
∴OF=OE,
∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2,
∴(8﹣x)2+42=x2,解得x=5,
即菱形的边长为5;
②在Rt△ABC中,AC==4,
∴OA=AC=2,
在Rt△AOE中,AE=5,
OE==,
∴EF=2OE=2.
24.见解析
【解析】
【分析】
(1)可通过全等三角形来证明简单的线段相等,△COD和△BOE中,已知了CO=BO,∠COD=∠BOE,CD∥BE,因此不难得出两三角形全等,进而可得出CD=BE.
(2)需先证明四边形AFCE是平行四边形,那么邻边相等的平行四边形是菱形.
【详解】
(1)∵CD∥BE,
∴∠CDE=∠DEB.
∵O是边BC的中点,
∴CO=BO.
在△COD和△BOE中,
∴△COD≌△BOE(AAS).
∴CD=BE.
(2)∵CD∥BE,CD=BE,
∴四边形BECD是平行四边形.
∵∠ABD=2∠BED,∠ABD=∠BED+∠BDE,
∴∠BED=∠BDE.
∴BD=BE.
∴四边形BECD是菱形.
25.(1)见解析;(2)见解析.
【详解】
(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠ABC=∠90?,
在Rt△ABD和Rt△CAE中,∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠ACE.
∵∠DAB+∠DBA=90?,∠EAC+∠ACE=90?,
∴∠BAD+∠CAE=90?.
∠BAC=180?-(∠BAD+∠CAE)=90?.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD=Rt△ACE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90?,即∠BAC=90°,
∴AB⊥AC.
26.(2)证明见解析;(3)成立,理由见解析
【详解】
试题分析:(2)在AB上截取AM=EC,然后证明∠EAM=FEC,∠AME=∠ECF=135°,再利用“角边角”证明△AEM和△EFC全等,然后根据全等三角形对应边相等即可证明;
(3)延长BA到M,使AM=CE,然后证明∠BME=45°,从而得到∠BME=∠ECF,再利用两直线平行,内错角相等证明∠DAE=∠BEA,然后得到∠MAE=∠CEF,再利用“角边角”证明△MAE和△CEF全等,根据全等三角形对应边相等即可得证.
试题解析:(2)探究2,证明:在AB上截取AM=EC,连接ME,
由(1)知∠EAM=∠FEC,
∵AM=EC,AB=BC,
∴BM=BE,
∴∠BME=45°,
∴∠AME=∠ECF=135°,
∵∠AEF=90°,
∴∠FEC+∠AEB=90°,
又∵∠EAM+∠AEB=90°,
∴∠EAM=∠FEC,
在△AEM和△EFC中,
,
∴△AEM≌△EFC(ASA),
∴AE=EF;
(3)探究3:成立,
证明:延长BA到M,使AM=CE,连接ME,
∴BM=BE,
∴∠BME=45°,
∴∠BME=∠ECF=45°,
又∵AD∥BE,
∴∠DAE=∠BEA,
又∵∠MAD=∠AEF=90°,
∴∠DAE+∠MAD=∠BEA+∠AEF,
即∠MAE=∠CEF,
在△MAE和△CEF中,
,
∴△MAE≌△CEF(ASA),
∴AE=EF.
答案第1页,总2页
答案第1页,总2页
选择题(本大题共有8个小题,每小题3分,共24分)
1.下列图案既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
2.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF
B.∠A=∠D
C.∠B=∠C
D.AB=
CD
3.如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于(
)
A.3.5
B.4
C.7
D.14
4.如图,矩形纸片中,,,将沿折叠,使点落在点处,交于点,则的长等于(
)
A.
B.
C.
D.
5.一个多边形的外角和是内角和的,这个多边形的边数为(
)
A.5
B.6
C.7
D.8
6.如图在中,于,于,为的中点,,的周长为13,则的长是
A.6
B.8
C.10
D.12
7.把一块等腰直角三角尺和直尺如图放置,如果,则的度数为
A.
B.
C.
D.
8.如图,已知点P是∠AOB角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,DM=4cm,如果点C是OB上一个动点,则PC的最小值为( )
A.2
B.
C.4
D.
填空题(本大题共8个小题,每小题3分,共24分)
9.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长_______.
10.如图,在Rt△BAC和Rt△BDC中,∠BAC=∠BDC=90°,O是BC的中点,连接AO、DO.若AO=3,则DO的长为_____.
11.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,S△BDC=4,BC=8,则AD=_________.
12.如图,将一张直角三角形纸片对折,使点B、C重合,折痕为DE,连接DC,若AC=6cm,∠ACB=90°,∠B=30°,则△ADC的周长是_____cm.
13.如图,在□ABCD中,AC,BD相交于点O,AB=10cm,AD=8cm,AC⊥BC,则OB=
_________cm.
14.已知一个直角三角形斜边上的中线长为6
cm,那么这个直角三角形的斜边长为______cm.
15.如图,在正方形ABCD中,对角线为AC,在BC延长线上取一点F,有AC=CF,AF与DC相交于点E,AB=4,则CF=_____,∠AEC=_____.
16.如图,在中,,,,和分别是其外角和的角平分线,延长和相交于点E,则_____度,_____.
三、解答题
17.已知:如图,在△ABC中,AB=13,AC=20,AD=12,且AD⊥BC,垂足为点D,求BC的长.
18.如图,直角三角形中,,,,,过点作于点.
(1)找出图中相等的锐角,并说明理由.
(2)求出点到直线的距离以及点到直线的距离.
解:(1)(已知),
,
,
,
.
同理可证,
.
(2)点到直线的距离 .
到直线的距离为线段 的长度.
(填线段名称).
,,,代入上式,解得
.
19.如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.
求证:△BCE≌△DCF;
20.如图,在和中,,,AC与BD相交于点O.
(1)求证:;
(2)是何种三角形?
21.如图,在△ABC中,AB,BC,CA的中点分别是点E,F,G,AD是高,连接ED,EF,FG,DG.求证:∠EDG=∠EFG.
22.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
23.将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,
①求菱形的边长;
②求折痕EF的长.
24.已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
25.如图,在中,,是过点的直线,于,于点;
(1)若、在的同侧(如图所示)且.求证:;
(2)若、在的两侧(如图所示),且,其他条件不变,与仍垂直吗?若是请给出证明;若不是,请说明理由.
26.如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(
)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
试卷第2页,总2页
试卷第1页,总1页
参考答案
1.A
2.D
3.A
4.A
5.C
6.B
7.B
8.C
9.2
10.3
11.1
12.18
13.
14.12
15.
112.5°
16.45°
6
17.21
【解析】
【详解】
∵AB=13,AC=20,AD=12,AD⊥BC,
∴Rt△ABD中,BD===5,
Rt△ACD中,CD===16,
∴BC=BD+CD=5+16=21.
18.(1)
∠2;∠2;同角的余角相等;∠B;
(2)12;CD;AC;BC;AB;CD;.
【详解】
(1)CD⊥AB(已知),
∴∠CDA=90?
∴∠A+∠1=90?,
∵∠1+∠2=90?,
∴∠A=∠2
同角的余角相等).
同理可证,
∴∠1=∠B.
故答案为∠2;∠2;同角的余角相等;∠B;
(2)点A到直线BC的距离=12cm.
C到直线AB的距离为线段CD的长度.
S△ABC=AC×BC=AB×CD.
∵AC=12,BC=5,AB=13,代入上式,解得
CD=cm.
故答案为5;
CD;AC;BC;AB;CD;.
19.证明见解析
【解析】
试题分析:由正方形的性质得出BC=DC,∠BCE=∠DCF=90°,由SAS证明△BCE≌△DCF.
试题解析:
证明:在正方形ABCD中
BC=DC,∠BCE=∠DCF=90°,
在△BCE与△DCF中,
∴△BCE≌△DCF.
20.(1)见解析;(2)△OBC是等腰三角形,理由见解析.
【详解】
(1)∵∠A=∠D=90°,
∴在Rt△ABC和Rt△DCB中,,
∴Rt△ABC≌Rt△DCB(HL);
(2)△OBC是等腰三角形,
理由:∵Rt△ABC≌Rt△DCB,
∴∠ACB=∠DBC,
∴OB=OC,
∴△OBC是等腰三角形.
21.见解析.
【解析】
证明:连接EG.
∵点E,F分别是AB,BC的中点,∴EF为△ABC的中位线,
∴EF=AC.
又∵AD⊥BC,∴∠ADC=90°,
DG为Rt△ADC斜边上的中线,
∴DG=AC,∴DG=EF
.同理可证DE=FG.
又∵EG=GE,
∴△EFG≌△GDE(SSS),
∴∠EDG=∠EFG.
22.(1)见解析;(2)四边形BECD是菱形,理由见解析;(3)当∠A=45°时,四边形BECD是正方形,理由见解析
【详解】
(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD(直角三角形斜边上的中线等于斜边的一半),
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:
解:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC,
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
23.(1)见解析;(2)①5;②2.
【详解】
(1)∵矩形ABCD折叠使A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,
∴∠FAC=∠ECA,在△AOF和△COE中,
∴△AOF≌△COE,
∴OF=OE,
∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BC﹣CE=8﹣x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2,
∴(8﹣x)2+42=x2,解得x=5,
即菱形的边长为5;
②在Rt△ABC中,AC==4,
∴OA=AC=2,
在Rt△AOE中,AE=5,
OE==,
∴EF=2OE=2.
24.见解析
【解析】
【分析】
(1)可通过全等三角形来证明简单的线段相等,△COD和△BOE中,已知了CO=BO,∠COD=∠BOE,CD∥BE,因此不难得出两三角形全等,进而可得出CD=BE.
(2)需先证明四边形AFCE是平行四边形,那么邻边相等的平行四边形是菱形.
【详解】
(1)∵CD∥BE,
∴∠CDE=∠DEB.
∵O是边BC的中点,
∴CO=BO.
在△COD和△BOE中,
∴△COD≌△BOE(AAS).
∴CD=BE.
(2)∵CD∥BE,CD=BE,
∴四边形BECD是平行四边形.
∵∠ABD=2∠BED,∠ABD=∠BED+∠BDE,
∴∠BED=∠BDE.
∴BD=BE.
∴四边形BECD是菱形.
25.(1)见解析;(2)见解析.
【详解】
(1)证明:∵BD⊥DE,CE⊥DE,
∴∠ADB=∠ABC=∠90?,
在Rt△ABD和Rt△CAE中,∵,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠ACE.
∵∠DAB+∠DBA=90?,∠EAC+∠ACE=90?,
∴∠BAD+∠CAE=90?.
∠BAC=180?-(∠BAD+∠CAE)=90?.
∴AB⊥AC.
(2)AB⊥AC.理由如下:
同(1)一样可证得Rt△ABD=Rt△ACE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90?,即∠BAC=90°,
∴AB⊥AC.
26.(2)证明见解析;(3)成立,理由见解析
【详解】
试题分析:(2)在AB上截取AM=EC,然后证明∠EAM=FEC,∠AME=∠ECF=135°,再利用“角边角”证明△AEM和△EFC全等,然后根据全等三角形对应边相等即可证明;
(3)延长BA到M,使AM=CE,然后证明∠BME=45°,从而得到∠BME=∠ECF,再利用两直线平行,内错角相等证明∠DAE=∠BEA,然后得到∠MAE=∠CEF,再利用“角边角”证明△MAE和△CEF全等,根据全等三角形对应边相等即可得证.
试题解析:(2)探究2,证明:在AB上截取AM=EC,连接ME,
由(1)知∠EAM=∠FEC,
∵AM=EC,AB=BC,
∴BM=BE,
∴∠BME=45°,
∴∠AME=∠ECF=135°,
∵∠AEF=90°,
∴∠FEC+∠AEB=90°,
又∵∠EAM+∠AEB=90°,
∴∠EAM=∠FEC,
在△AEM和△EFC中,
,
∴△AEM≌△EFC(ASA),
∴AE=EF;
(3)探究3:成立,
证明:延长BA到M,使AM=CE,连接ME,
∴BM=BE,
∴∠BME=45°,
∴∠BME=∠ECF=45°,
又∵AD∥BE,
∴∠DAE=∠BEA,
又∵∠MAD=∠AEF=90°,
∴∠DAE+∠MAD=∠BEA+∠AEF,
即∠MAE=∠CEF,
在△MAE和△CEF中,
,
∴△MAE≌△CEF(ASA),
∴AE=EF.
答案第1页,总2页
答案第1页,总2页
同课章节目录
