五年级数学下册试题 一课一练 2.2展开与折叠 北师大版(含答案)
文档属性
| 名称 | 五年级数学下册试题 一课一练 2.2展开与折叠 北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 385.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 10:39:50 | ||
图片预览


文档简介
2.2展开与折叠
一、填空题
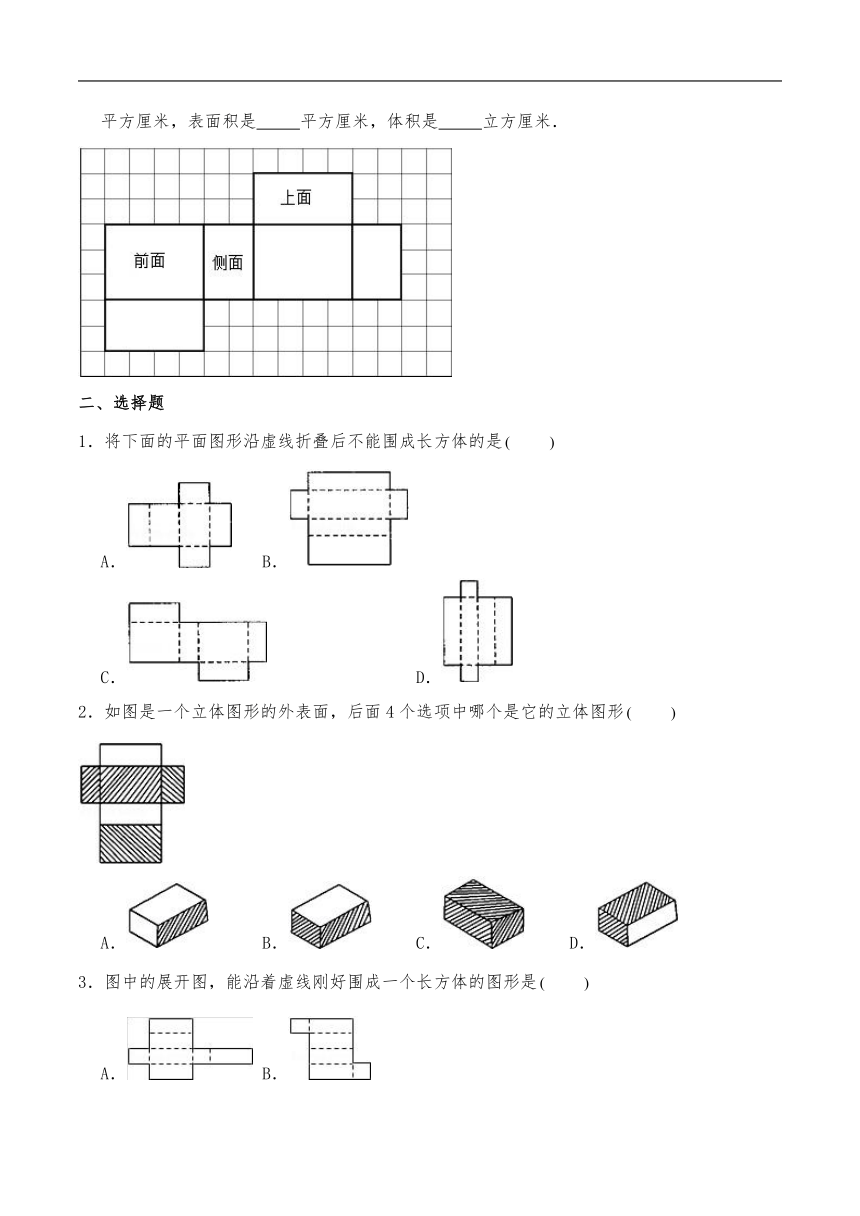
1.在图2中: 个 个.
2.一张长方形纸如图折叠,, .
3.一位魔术师把一根1米长的带子,按20厘米折一折的方法全部折好,折成一捆,再在它的中间剪开,猜猜,这时带子是 段.
4.下面是一个长方体的展开图,这个长方体的长是 ,宽是 ,高是 .
5.从一个方向观察长方体纸盒,最多能看到长方体纸盒的 个面.
6.如图,把这个展开图折成一个长方体,
(1)如果面在底部,那么 面在上面.
(2)如果面在前面,从左面看是面,那么 面在上面.
7.下面是一个长方形的表面展开图(每个小方格的边长表示1厘米).这个长方体的底面积是
平方厘米,表面积是
平方厘米,体积是
立方厘米.
二、选择题
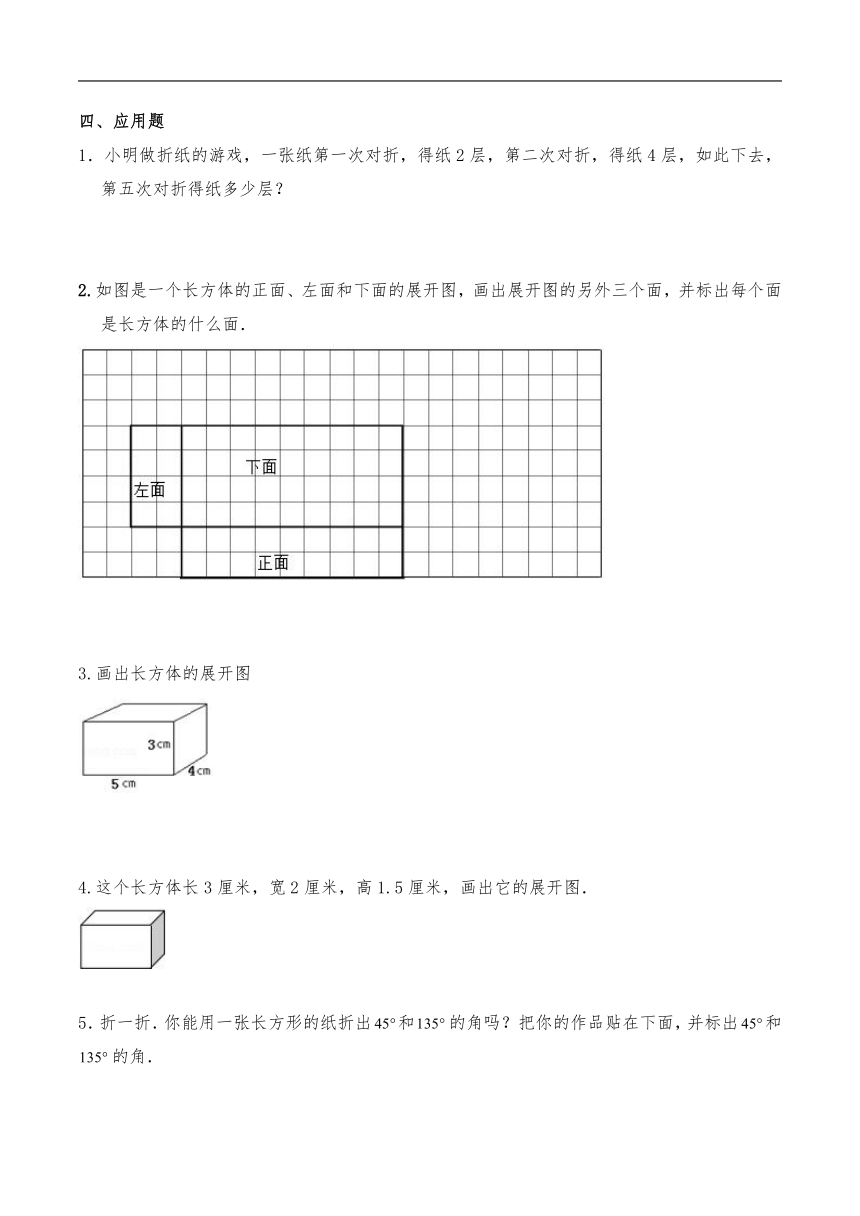
1.将下面的平面图形沿虚线折叠后不能围成长方体的是
A.
B.
C.
D.
2.如图是一个立体图形的外表面,后面4个选项中哪个是它的立体图形
A.
B.
C.
D.
3.图中的展开图,能沿着虚线刚好围成一个长方体的图形是
A.
B.
C.
D.
4.如图是一个长方体的展开图,如果①是长方体的下面,那么 是和它相对的上面
A.5
B.④
C.3
D.2
5.将一张圆形纸对折三次,得到的角是
A.
B.
C.
D.
6.把一张长方形的纸对折再对折,打开后两条折痕
A.互相平行
B.互相垂直
C.可能互相平行,也可能互相垂直
7.把一张长方形纸对折3次,每份占整个长方形的
A.
B.
C.
8.将一张圆形的纸片先上下对折,再左右对折,得到的角的度数是
A.
B.
C.
三、判断题
1.如图是长方体的表面展开图,与⑥相对的面是③.(
)
2.一个长方体展开后,只能得到一种展开图.(
)
3.长方体的展开图折叠后不一定就能围成长方体.(
)
4.拿一张圆形的纸,把它对折再对折,得到的角是直角.(
)
5.正方形对折一次可以折成长方形,也可以折成三角形.(
)
6.一个长方形长是12厘米,宽6厘米,对折后一定能变成正方形.(
)
四、应用题
1.小明做折纸的游戏,一张纸第一次对折,得纸2层,第二次对折,得纸4层,如此下去,第五次对折得纸多少层?
2.如图是一个长方体的正面、左面和下面的展开图,画出展开图的另外三个面,并标出每个面是长方体的什么面.
3.画出长方体的展开图
4.这个长方体长3厘米,宽2厘米,高1.5厘米,画出它的展开图.
5.折一折.你能用一张长方形的纸折出和的角吗?把你的作品贴在下面,并标出和的角.
6.折正三角形
用一张正方形纸片折出一个正三角形,你有几种不同的折法?其中面积最大的是哪一种?
要求:①说明折法,配以图示;②说明每种折法的依据.
7.将一张正方形纸对折后,出现一条折痕,将两个角折到刚刚的折痕上,如图,如果形成的角中,那么是多少度?
8.在展开图上找出相对的面,并用上、下、左、右标出,再用、、标出三条边.
答案
一、填空题
1.360,2,4.
2.50.
3.6.
4.25,5,40.
5.3.
6.,或.
7.8,52,24.
二、选择题
1..2..3..4..5..6..7..8..
三、判断题
1..2..3..4..5..6..
四、应用题
1.解:(层
答:第五次对折得纸32层.
2.解:根据分析,作图如下:
3.解:
4.解:如图:
5.解:如图所示:
.
6.解:方法一(如图)
先把正方形纸对折,展开后折痕为,再把折到折痕上的点,也折到点,由于,所以三角形为正三角形
方法二(如图)
在正方形纸一个角分别折出两个的角,剩下的角是,沿这两条拆线的另个两个点折,中间的大三角形为顶角的等腰三角形,顶角为的三角形是正三角形.
第一种方法所折出的正三角形的边是长方形边长,第二种折法的折出的三角形的边长大于正方形边长.第二种折法折出的正三角形的面积最大.
7.解:如图
因为,,
所以
答:是120度.
8.解:在展开图上找出相对的面,并用上、下、左、右标出,再用,,标出每条棱(下图)
一、填空题
1.在图2中: 个 个.
2.一张长方形纸如图折叠,, .
3.一位魔术师把一根1米长的带子,按20厘米折一折的方法全部折好,折成一捆,再在它的中间剪开,猜猜,这时带子是 段.
4.下面是一个长方体的展开图,这个长方体的长是 ,宽是 ,高是 .
5.从一个方向观察长方体纸盒,最多能看到长方体纸盒的 个面.
6.如图,把这个展开图折成一个长方体,
(1)如果面在底部,那么 面在上面.
(2)如果面在前面,从左面看是面,那么 面在上面.
7.下面是一个长方形的表面展开图(每个小方格的边长表示1厘米).这个长方体的底面积是
平方厘米,表面积是
平方厘米,体积是
立方厘米.
二、选择题
1.将下面的平面图形沿虚线折叠后不能围成长方体的是
A.
B.
C.
D.
2.如图是一个立体图形的外表面,后面4个选项中哪个是它的立体图形
A.
B.
C.
D.
3.图中的展开图,能沿着虚线刚好围成一个长方体的图形是
A.
B.
C.
D.
4.如图是一个长方体的展开图,如果①是长方体的下面,那么 是和它相对的上面
A.5
B.④
C.3
D.2
5.将一张圆形纸对折三次,得到的角是
A.
B.
C.
D.
6.把一张长方形的纸对折再对折,打开后两条折痕
A.互相平行
B.互相垂直
C.可能互相平行,也可能互相垂直
7.把一张长方形纸对折3次,每份占整个长方形的
A.
B.
C.
8.将一张圆形的纸片先上下对折,再左右对折,得到的角的度数是
A.
B.
C.
三、判断题
1.如图是长方体的表面展开图,与⑥相对的面是③.(
)
2.一个长方体展开后,只能得到一种展开图.(
)
3.长方体的展开图折叠后不一定就能围成长方体.(
)
4.拿一张圆形的纸,把它对折再对折,得到的角是直角.(
)
5.正方形对折一次可以折成长方形,也可以折成三角形.(
)
6.一个长方形长是12厘米,宽6厘米,对折后一定能变成正方形.(
)
四、应用题
1.小明做折纸的游戏,一张纸第一次对折,得纸2层,第二次对折,得纸4层,如此下去,第五次对折得纸多少层?
2.如图是一个长方体的正面、左面和下面的展开图,画出展开图的另外三个面,并标出每个面是长方体的什么面.
3.画出长方体的展开图
4.这个长方体长3厘米,宽2厘米,高1.5厘米,画出它的展开图.
5.折一折.你能用一张长方形的纸折出和的角吗?把你的作品贴在下面,并标出和的角.
6.折正三角形
用一张正方形纸片折出一个正三角形,你有几种不同的折法?其中面积最大的是哪一种?
要求:①说明折法,配以图示;②说明每种折法的依据.
7.将一张正方形纸对折后,出现一条折痕,将两个角折到刚刚的折痕上,如图,如果形成的角中,那么是多少度?
8.在展开图上找出相对的面,并用上、下、左、右标出,再用、、标出三条边.
答案
一、填空题
1.360,2,4.
2.50.
3.6.
4.25,5,40.
5.3.
6.,或.
7.8,52,24.
二、选择题
1..2..3..4..5..6..7..8..
三、判断题
1..2..3..4..5..6..
四、应用题
1.解:(层
答:第五次对折得纸32层.
2.解:根据分析,作图如下:
3.解:
4.解:如图:
5.解:如图所示:
.
6.解:方法一(如图)
先把正方形纸对折,展开后折痕为,再把折到折痕上的点,也折到点,由于,所以三角形为正三角形
方法二(如图)
在正方形纸一个角分别折出两个的角,剩下的角是,沿这两条拆线的另个两个点折,中间的大三角形为顶角的等腰三角形,顶角为的三角形是正三角形.
第一种方法所折出的正三角形的边是长方形边长,第二种折法的折出的三角形的边长大于正方形边长.第二种折法折出的正三角形的面积最大.
7.解:如图
因为,,
所以
答:是120度.
8.解:在展开图上找出相对的面,并用上、下、左、右标出,再用,,标出每条棱(下图)
