2020—2021人教版八年级数学下册第18章平行四边形解答题典型必练(二)(word版含答案)
文档属性
| 名称 | 2020—2021人教版八年级数学下册第18章平行四边形解答题典型必练(二)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-27 10:10:58 | ||
图片预览

文档简介
人教版八年级数学下册第18章平行四边形
解答题典型必练(二)
1.如图,已知正方形ABCD,点E在BC上,点F在CD延长线上,BE=DF
(1)求证:AE=AF;
(2)若BD与EF交于点M,连接AM,试判断AM与EF的数量与位置关系,并说明理由.
2.正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
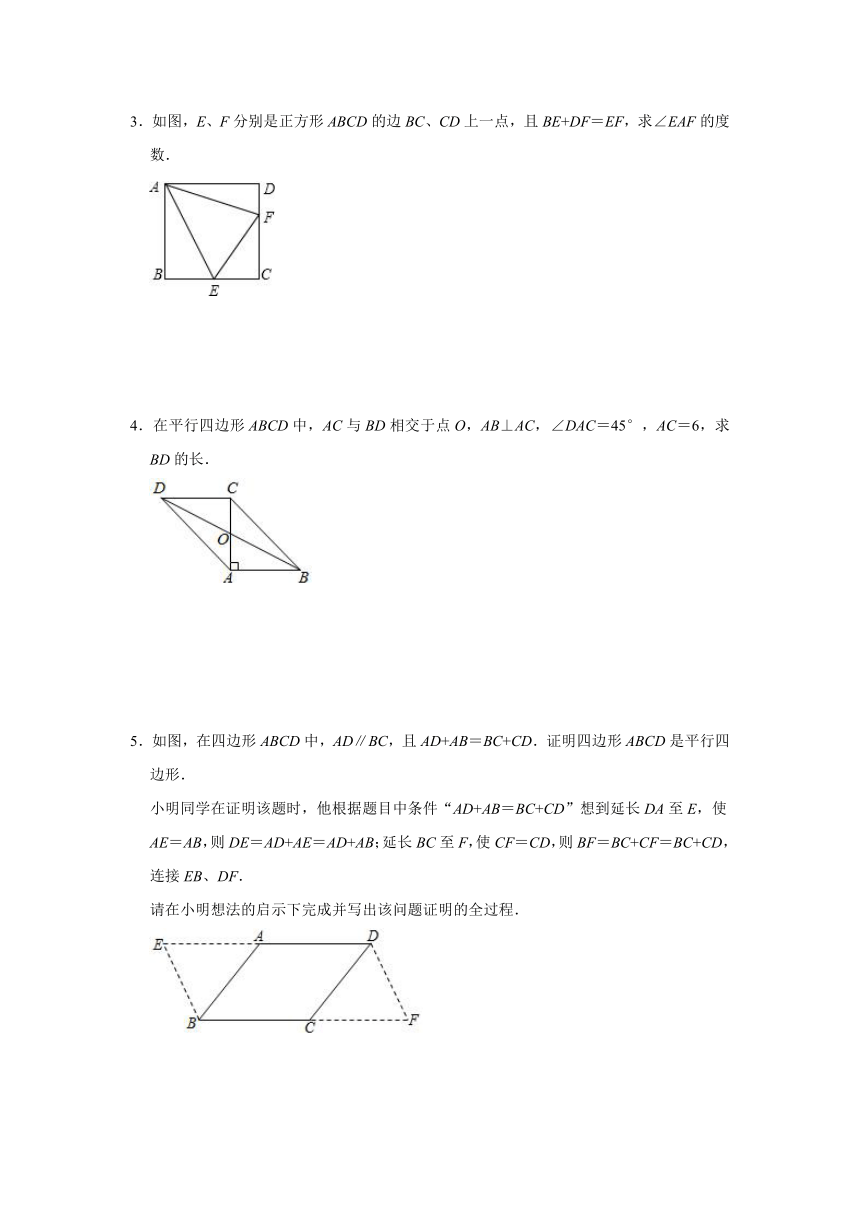
3.如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,求∠EAF的度数.
4.在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=6,求BD的长.
5.如图,在四边形ABCD中,AD∥BC,且AD+AB=BC+CD.证明四边形ABCD是平行四边形.
小明同学在证明该题时,他根据题目中条件“AD+AB=BC+CD”想到延长DA至E,使AE=AB,则DE=AD+AE=AD+AB;延长BC至F,使CF=CD,则BF=BC+CF=BC+CD,连接EB、DF.
请在小明想法的启示下完成并写出该问题证明的全过程.
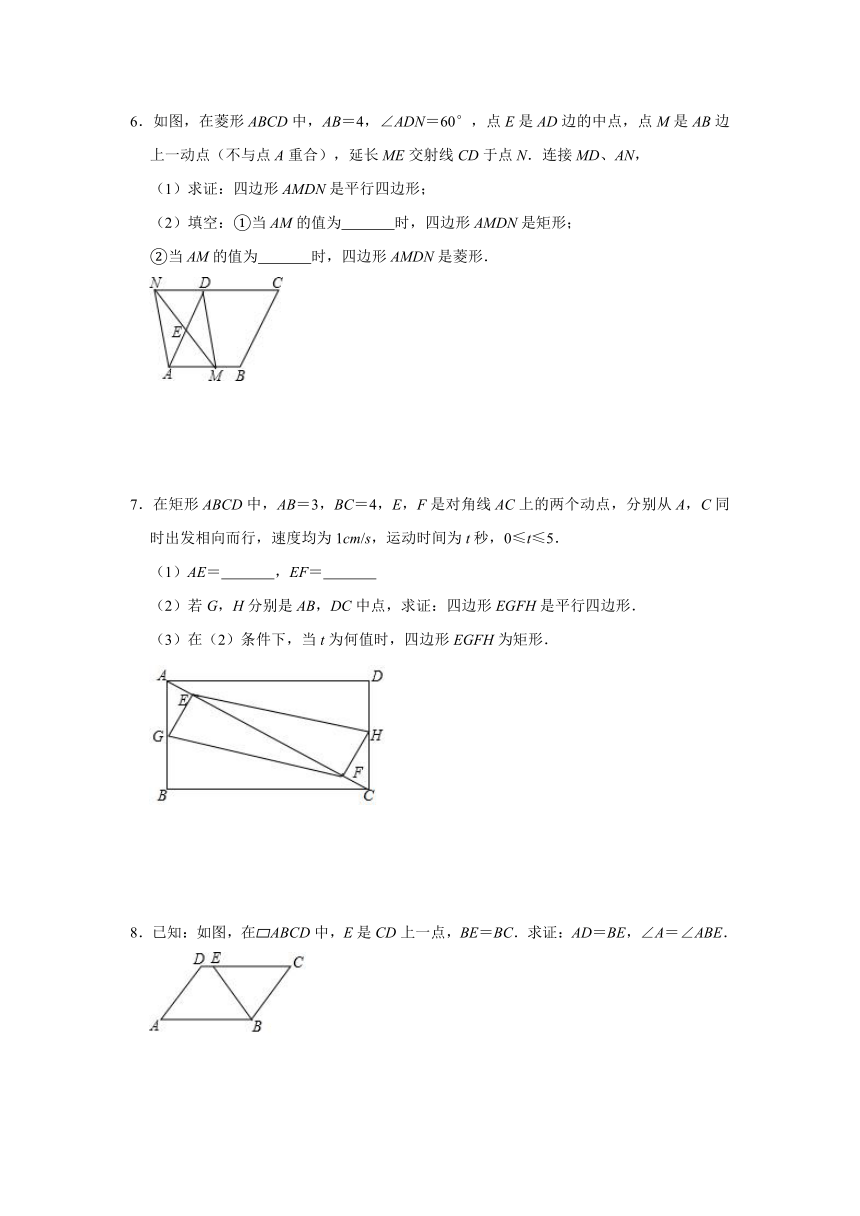
6.如图,在菱形ABCD中,AB=4,∠ADN=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N.连接MD、AN,
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为
时,四边形AMDN是矩形;
②当AM的值为
时,四边形AMDN是菱形.
7.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE=
,EF=
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
8.已知:如图,在?ABCD中,E是CD上一点,BE=BC.求证:AD=BE,∠A=∠ABE.
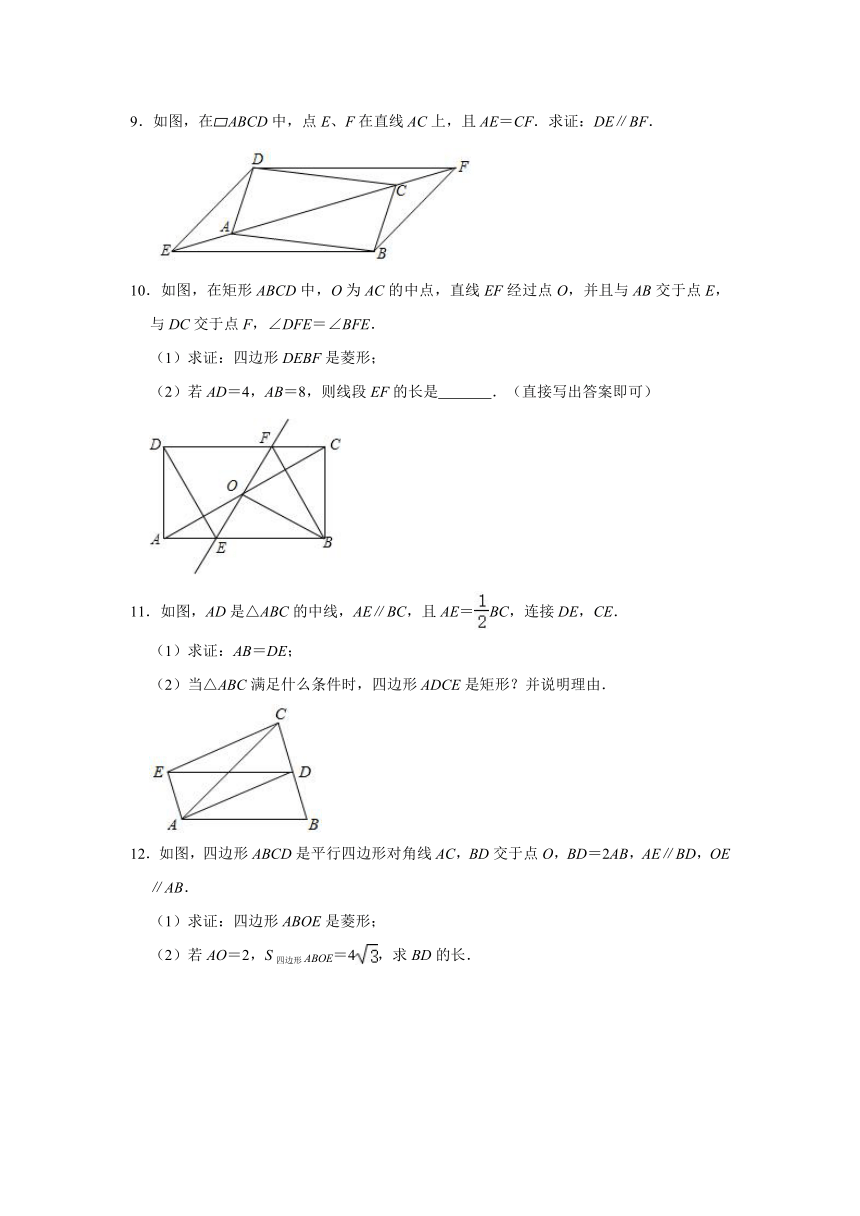
9.如图,在?ABCD中,点E、F在直线AC上,且AE=CF.求证:DE∥BF.
10.如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是
.(直接写出答案即可)
11.如图,AD是△ABC的中线,AE∥BC,且AE=BC,连接DE,CE.
(1)求证:AB=DE;
(2)当△ABC满足什么条件时,四边形ADCE是矩形?并说明理由.
12.如图,四边形ABCD是平行四边形对角线AC,BD交于点O,BD=2AB,AE∥BD,OE∥AB.
(1)求证:四边形ABOE是菱形;
(2)若AO=2,S四边形ABOE=4,求BD的长.
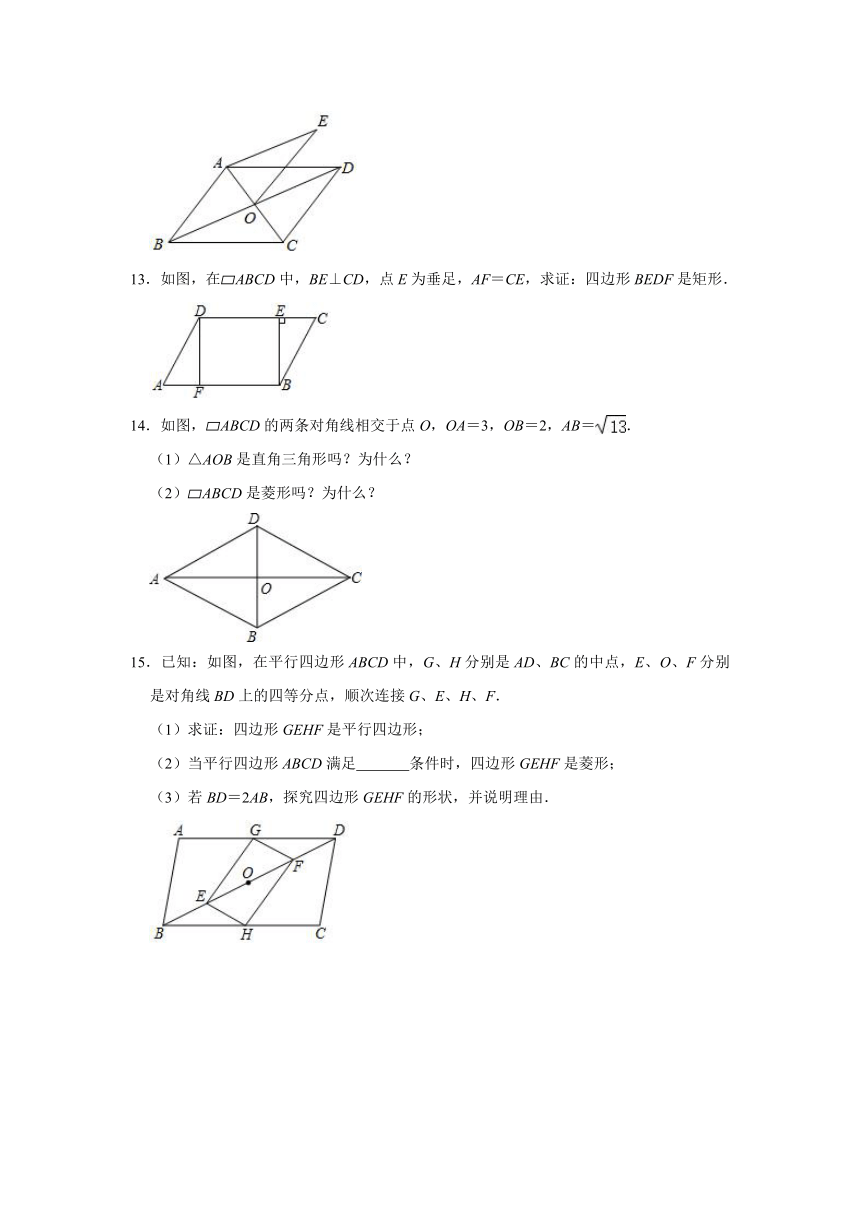
13.如图,在?ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
14.如图,?ABCD的两条对角线相交于点O,OA=3,OB=2,AB=.
(1)△AOB是直角三角形吗?为什么?
(2)?ABCD是菱形吗?为什么?
15.已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当平行四边形ABCD满足
条件时,四边形GEHF是菱形;
(3)若BD=2AB,探究四边形GEHF的形状,并说明理由.
参考答案
1.(1)证明:∵四边形ABCD为正方形,
∴∠ABE=∠ADC=∠ADF=90°,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)AM⊥EF,AM=EF,理由是:
由(1)得:△ABE≌△ADF,
∴∠FAD=∠EAB,
∴∠FAE=∠DAB=90°,
∴△FAE是直角三角形,
如图,过E作EN∥CD,交BD于N,
∴∠MNE=∠MDF,∠MEN=∠MFD,
∵四边形ABCD为正方形,
∴∠NBE=45°,
∴△NBE是等腰直角三角形,
∴EN=BE=DF,
在△MNE和△MDF中,
∵,
∴△MNE≌△MDF(ASA),
∴EM=FM,
∵AE=AF,
∴AM⊥EF,AM=EF.
2.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF,
∴EF=CF+AE;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
3.解:延长EB使得BG=DF,连接AG,
在△ABG和△ADF中,
,
可得△ABG≌△ADF(SAS),
∴∠DAF=∠BAG,AF=AG,
又∵EF=DF+BE=EB+BG=EG,AE=AE,
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SSS),
∴∠EAG=∠EAF,
∵∠DAF+∠EAF+∠BAE=90°
∴∠EAG+∠EAF=90°,
∴∠EAF=45°.
4.解:∵四边形ABCD是平行四边形,
∴,BD=2OD,CD∥AB,
∵AB⊥AC,
∴AC⊥CD,
∵∠DAC=45°,
∴CD=AC=6,
在Rt△COD中,,
∴.
5.证明:法一:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AB=CD,
∵AD+AB=BC+CD,
∴AD=BC,
∴四边形ABCD是平行四边形.
法二:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠EAB=∠DCF,
又∵AD∥BC,
∴∠EAB=∠ABC,
∴∠ABC=∠DCF,
∴AB∥CD,
∴四边形ABCD为平行四边形.
6.(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,AD=AB=4,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)解:①当AM的值为2时,四边形AMDN是矩形.理由如下:
∵AM=2=AD=AE,∠DAM=60°,
∴△AEM是等边三角形,
∴AE=EM=DE,∠AEM=60°,
∴∠ADM=30°
∵∠DAM=60°,
∴∠AMD=90°,
∴平行四边形AMDN是矩形;
故答案为:2;
②当AM的值为4时,四边形AMDN是菱形.理由如下:
∵AM=4,
∴AM=AD=4,
∴△AMD是等边三角形,
∴AM=DM,
∴平行四边形AMDN是菱形,
故答案为:4.
7.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC===5,
由题意得:AE=CF=t,
∴EF相遇前为:EF=AC﹣AE﹣CF=5﹣2t;
EF相遇后为:EF=AE+CF﹣AC=2t﹣5;
故答案为:t,5﹣2t或2t﹣5;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC===5,∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(3)解:如图所示,连接GH,
由(2)可知四边形EGFH是平行四边形
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4,
解得:t=0.5.
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5
即:当t为0.5秒或4.5时,四边形EGFH为矩形
8.证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD=BC,
∴∠ABE=∠BEC,
∵BE=BC,
∴AD=BE,∠C=∠BEC,
∴∠A=∠ABE.
9.证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAF=∠BCE,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴∠DEA=∠BFC,
∴DE∥BF.
10.(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,DC=AB,
∴∠OAE=∠OCF,
∵OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
又∵∠DFE=∠BFE,∠DFE=∠FEB,
∴∠BFE=∠BEF,
∴BE=BF,
∴四边形DEBF是菱形.
(2)如图,作FH⊥AB于H.设DF=BF=x,
在Rt△BCF中,∠BCF=90°,BC=AD=4,CF=4﹣x,
∴x2=42+(8﹣x)2,
∴x=5,
∴DF=5,CF=3,
∵∠FHB=∠HBC=∠BCF=90°,
∴四边形BCFH是矩形,
∴CF=BH=3,FH=BC=4,
∵BF=DF=5,
∴EH=2,
∴EF===2,
故答案为.
11.证明:(1)∵AD是△ABC的中线,
∴BD=CD=BC,
∵AE=BC,
∴AE=BD,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AB=DE;
(2)当△ABC满足AB=AC时,四边形ADCE是矩形,
∵AE=BC,BD=CD=BC,
∴AE=CD,
∵AE∥BC,
∴四边形ADCE是平行四边形,
∵AB=DE,
∴当AB=AC时,AC=DE,
∴四边形ADCE是矩形.
12.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD=BD,
∵BD=2AB,
∴AB=OB,
∵AE∥BD,OE∥AB,
∴四边形ABOE是平行四边形,
∵AB=OB,
∴四边形ABOE是菱形;
(2)解:连接BE,交OA于F,如图所示:
∵四边形ABOE是菱形,
∴OA⊥BE,AF=OF=OA=1,BF=EF=BE,
∵S四边形ABOE=4,
S四边形ABOE=OA?BE=×2×BE=BE,
∴BE=4,
∴BF=2,
∴OB===,
∴BD=2OB=2.
13.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形BEDF是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形BEDF是矩形.
14.解:(1)△AOB是直角三角形;理由如下:
∵32+22=()2,
∴AO2+BO2=AB2,
∴∠AOB=90°,
∴△AOB是直角三角形;
(2)?ABCD是菱形;理由如下:
由(1)得:∠AOB=90°,
∴AC⊥BD,
∵四边形ABCD是平行四边形,
∴?ABCD是菱形.
15.(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,
∴E、F分别为OB、OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理:EH∥OC,EH=OC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形;
(2)解:当?ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:
则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB∥GH,
∵AB⊥BD,
∴GH⊥BD,
∴GH⊥EF,
∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,
∴GH=AB,
∵BD=2AB,
∴AB=BD=EF,
∴GH=EF,
∴四边形GEHF是矩形.
解答题典型必练(二)
1.如图,已知正方形ABCD,点E在BC上,点F在CD延长线上,BE=DF
(1)求证:AE=AF;
(2)若BD与EF交于点M,连接AM,试判断AM与EF的数量与位置关系,并说明理由.
2.正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=CF+AE;
(2)当AE=2时,求EF的长.
3.如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,求∠EAF的度数.
4.在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=6,求BD的长.
5.如图,在四边形ABCD中,AD∥BC,且AD+AB=BC+CD.证明四边形ABCD是平行四边形.
小明同学在证明该题时,他根据题目中条件“AD+AB=BC+CD”想到延长DA至E,使AE=AB,则DE=AD+AE=AD+AB;延长BC至F,使CF=CD,则BF=BC+CF=BC+CD,连接EB、DF.
请在小明想法的启示下完成并写出该问题证明的全过程.
6.如图,在菱形ABCD中,AB=4,∠ADN=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N.连接MD、AN,
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为
时,四边形AMDN是矩形;
②当AM的值为
时,四边形AMDN是菱形.
7.在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE=
,EF=
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
8.已知:如图,在?ABCD中,E是CD上一点,BE=BC.求证:AD=BE,∠A=∠ABE.
9.如图,在?ABCD中,点E、F在直线AC上,且AE=CF.求证:DE∥BF.
10.如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是
.(直接写出答案即可)
11.如图,AD是△ABC的中线,AE∥BC,且AE=BC,连接DE,CE.
(1)求证:AB=DE;
(2)当△ABC满足什么条件时,四边形ADCE是矩形?并说明理由.
12.如图,四边形ABCD是平行四边形对角线AC,BD交于点O,BD=2AB,AE∥BD,OE∥AB.
(1)求证:四边形ABOE是菱形;
(2)若AO=2,S四边形ABOE=4,求BD的长.
13.如图,在?ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
14.如图,?ABCD的两条对角线相交于点O,OA=3,OB=2,AB=.
(1)△AOB是直角三角形吗?为什么?
(2)?ABCD是菱形吗?为什么?
15.已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当平行四边形ABCD满足
条件时,四边形GEHF是菱形;
(3)若BD=2AB,探究四边形GEHF的形状,并说明理由.
参考答案
1.(1)证明:∵四边形ABCD为正方形,
∴∠ABE=∠ADC=∠ADF=90°,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)AM⊥EF,AM=EF,理由是:
由(1)得:△ABE≌△ADF,
∴∠FAD=∠EAB,
∴∠FAE=∠DAB=90°,
∴△FAE是直角三角形,
如图,过E作EN∥CD,交BD于N,
∴∠MNE=∠MDF,∠MEN=∠MFD,
∵四边形ABCD为正方形,
∴∠NBE=45°,
∴△NBE是等腰直角三角形,
∴EN=BE=DF,
在△MNE和△MDF中,
∵,
∴△MNE≌△MDF(ASA),
∴EM=FM,
∵AE=AF,
∴AM⊥EF,AM=EF.
2.(1)证明:∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,AE=CM,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF,
∴EF=CF+AE;
(2)解:设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得EB2+BF2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,
则EF=5.
3.解:延长EB使得BG=DF,连接AG,
在△ABG和△ADF中,
,
可得△ABG≌△ADF(SAS),
∴∠DAF=∠BAG,AF=AG,
又∵EF=DF+BE=EB+BG=EG,AE=AE,
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SSS),
∴∠EAG=∠EAF,
∵∠DAF+∠EAF+∠BAE=90°
∴∠EAG+∠EAF=90°,
∴∠EAF=45°.
4.解:∵四边形ABCD是平行四边形,
∴,BD=2OD,CD∥AB,
∵AB⊥AC,
∴AC⊥CD,
∵∠DAC=45°,
∴CD=AC=6,
在Rt△COD中,,
∴.
5.证明:法一:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AB=CD,
∵AD+AB=BC+CD,
∴AD=BC,
∴四边形ABCD是平行四边形.
法二:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠EAB=∠DCF,
又∵AD∥BC,
∴∠EAB=∠ABC,
∴∠ABC=∠DCF,
∴AB∥CD,
∴四边形ABCD为平行四边形.
6.(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,AD=AB=4,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)解:①当AM的值为2时,四边形AMDN是矩形.理由如下:
∵AM=2=AD=AE,∠DAM=60°,
∴△AEM是等边三角形,
∴AE=EM=DE,∠AEM=60°,
∴∠ADM=30°
∵∠DAM=60°,
∴∠AMD=90°,
∴平行四边形AMDN是矩形;
故答案为:2;
②当AM的值为4时,四边形AMDN是菱形.理由如下:
∵AM=4,
∴AM=AD=4,
∴△AMD是等边三角形,
∴AM=DM,
∴平行四边形AMDN是菱形,
故答案为:4.
7.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,
∴AC===5,
由题意得:AE=CF=t,
∴EF相遇前为:EF=AC﹣AE﹣CF=5﹣2t;
EF相遇后为:EF=AE+CF﹣AC=2t﹣5;
故答案为:t,5﹣2t或2t﹣5;
(2)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC===5,∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,,
∴△AFG≌△CEH(SAS),
∴GF=HE,
同理:GE=HF,
∴四边形EGFH是平行四边形.
(3)解:如图所示,连接GH,
由(2)可知四边形EGFH是平行四边形
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5﹣2t=4,
解得:t=0.5.
②AE=CF=t,EF=5﹣2(5﹣t)=4,
解得:t=4.5
即:当t为0.5秒或4.5时,四边形EGFH为矩形
8.证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD=BC,
∴∠ABE=∠BEC,
∵BE=BC,
∴AD=BE,∠C=∠BEC,
∴∠A=∠ABE.
9.证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAF=∠BCE,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴∠DEA=∠BFC,
∴DE∥BF.
10.(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,DC=AB,
∴∠OAE=∠OCF,
∵OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
又∵∠DFE=∠BFE,∠DFE=∠FEB,
∴∠BFE=∠BEF,
∴BE=BF,
∴四边形DEBF是菱形.
(2)如图,作FH⊥AB于H.设DF=BF=x,
在Rt△BCF中,∠BCF=90°,BC=AD=4,CF=4﹣x,
∴x2=42+(8﹣x)2,
∴x=5,
∴DF=5,CF=3,
∵∠FHB=∠HBC=∠BCF=90°,
∴四边形BCFH是矩形,
∴CF=BH=3,FH=BC=4,
∵BF=DF=5,
∴EH=2,
∴EF===2,
故答案为.
11.证明:(1)∵AD是△ABC的中线,
∴BD=CD=BC,
∵AE=BC,
∴AE=BD,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AB=DE;
(2)当△ABC满足AB=AC时,四边形ADCE是矩形,
∵AE=BC,BD=CD=BC,
∴AE=CD,
∵AE∥BC,
∴四边形ADCE是平行四边形,
∵AB=DE,
∴当AB=AC时,AC=DE,
∴四边形ADCE是矩形.
12.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD=BD,
∵BD=2AB,
∴AB=OB,
∵AE∥BD,OE∥AB,
∴四边形ABOE是平行四边形,
∵AB=OB,
∴四边形ABOE是菱形;
(2)解:连接BE,交OA于F,如图所示:
∵四边形ABOE是菱形,
∴OA⊥BE,AF=OF=OA=1,BF=EF=BE,
∵S四边形ABOE=4,
S四边形ABOE=OA?BE=×2×BE=BE,
∴BE=4,
∴BF=2,
∴OB===,
∴BD=2OB=2.
13.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形BEDF是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形BEDF是矩形.
14.解:(1)△AOB是直角三角形;理由如下:
∵32+22=()2,
∴AO2+BO2=AB2,
∴∠AOB=90°,
∴△AOB是直角三角形;
(2)?ABCD是菱形;理由如下:
由(1)得:∠AOB=90°,
∴AC⊥BD,
∵四边形ABCD是平行四边形,
∴?ABCD是菱形.
15.(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,
∴E、F分别为OB、OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理:EH∥OC,EH=OC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形;
(2)解:当?ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:
则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB∥GH,
∵AB⊥BD,
∴GH⊥BD,
∴GH⊥EF,
∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,
∴GH=AB,
∵BD=2AB,
∴AB=BD=EF,
∴GH=EF,
∴四边形GEHF是矩形.
