2020-2021人教版八年级数学下册第18章平行四边形解答题典型必练(三)(word版含答案)
文档属性
| 名称 | 2020-2021人教版八年级数学下册第18章平行四边形解答题典型必练(三)(word版含答案) | 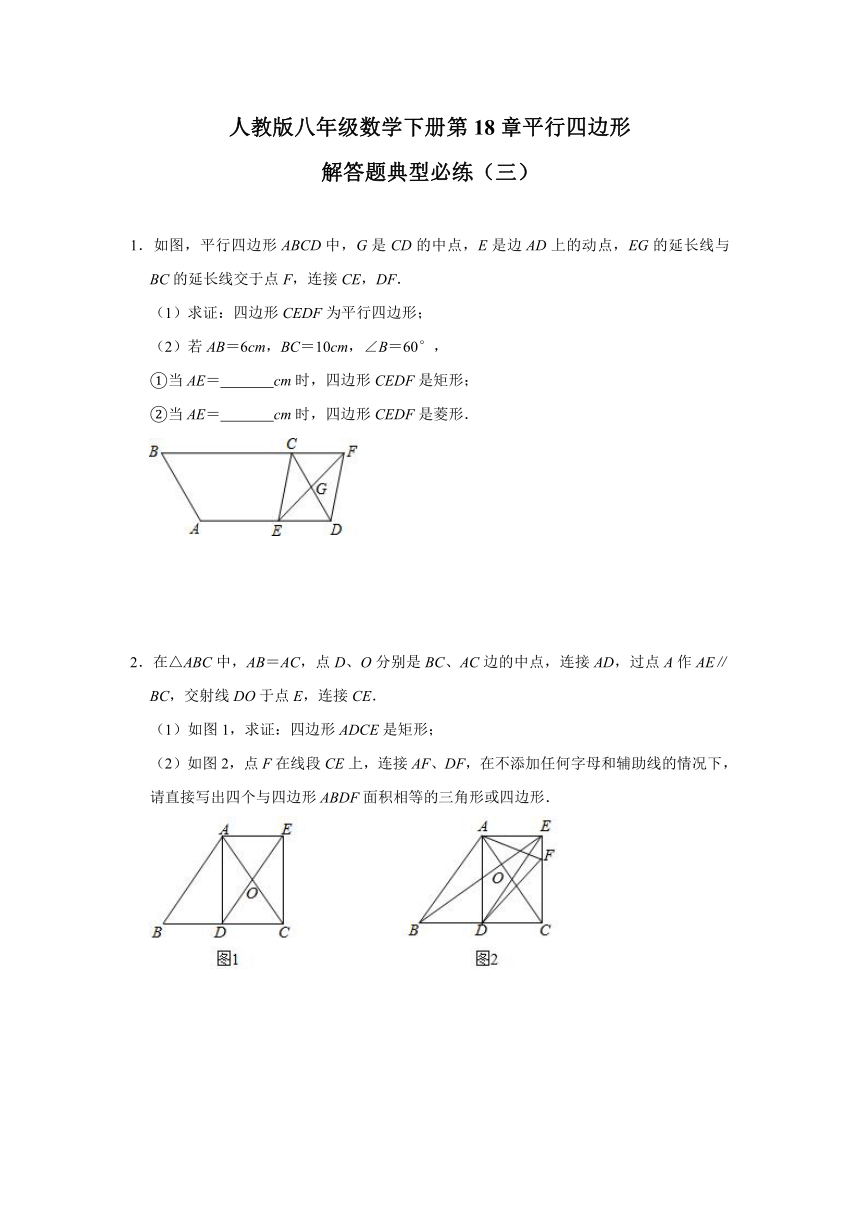 | |
| 格式 | zip | ||
| 文件大小 | 234.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-27 10:14:36 | ||
图片预览




文档简介
人教版八年级数学下册第18章平行四边形
解答题典型必练(三)
1.如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF为平行四边形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①当AE=
cm时,四边形CEDF是矩形;
②当AE=
cm时,四边形CEDF是菱形.
2.在△ABC中,AB=AC,点D、O分别是BC、AC边的中点,连接AD,过点A作AE∥BC,交射线DO于点E,连接CE.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,点F在线段CE上,连接AF、DF,在不添加任何字母和辅助线的情况下,请直接写出四个与四边形ABDF面积相等的三角形或四边形.
3.如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,顶点A(a,0),B(0,b)分别在x轴,y轴上,且满足.
(1)a=
,b=
;
(2)求点C的坐标;
(3)在平面直角坐标系中找一点D,使得点A,B,C,D组成的四边形为平行四边形.
4.我们定义:在四边形中,一条边上的两个角称为邻角,如果一条边上的邻角相等,且这条边对边上的邻角也相等,则把这样的四边形叫做“完美四边形”
初步运用:在“平行四边形、矩形和菱形”这三种特殊的四边形中,一定是“完美四边形”的是
.
问题探究:在完美四边形ABCD中,AD≠BC,∠B=60°,BD⊥DC,BC=6,求该完美四边形的周长与面积.
应用拓展:请你类比研究平行四边形及特殊四边形的方法,写出“完美四边形”的其中三条性质.
5.如图,?ABCD中,DF平分∠ADC交AC于点H,G为DH的中点.
(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=2,求GM;
(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC.求证:MC=2CG.
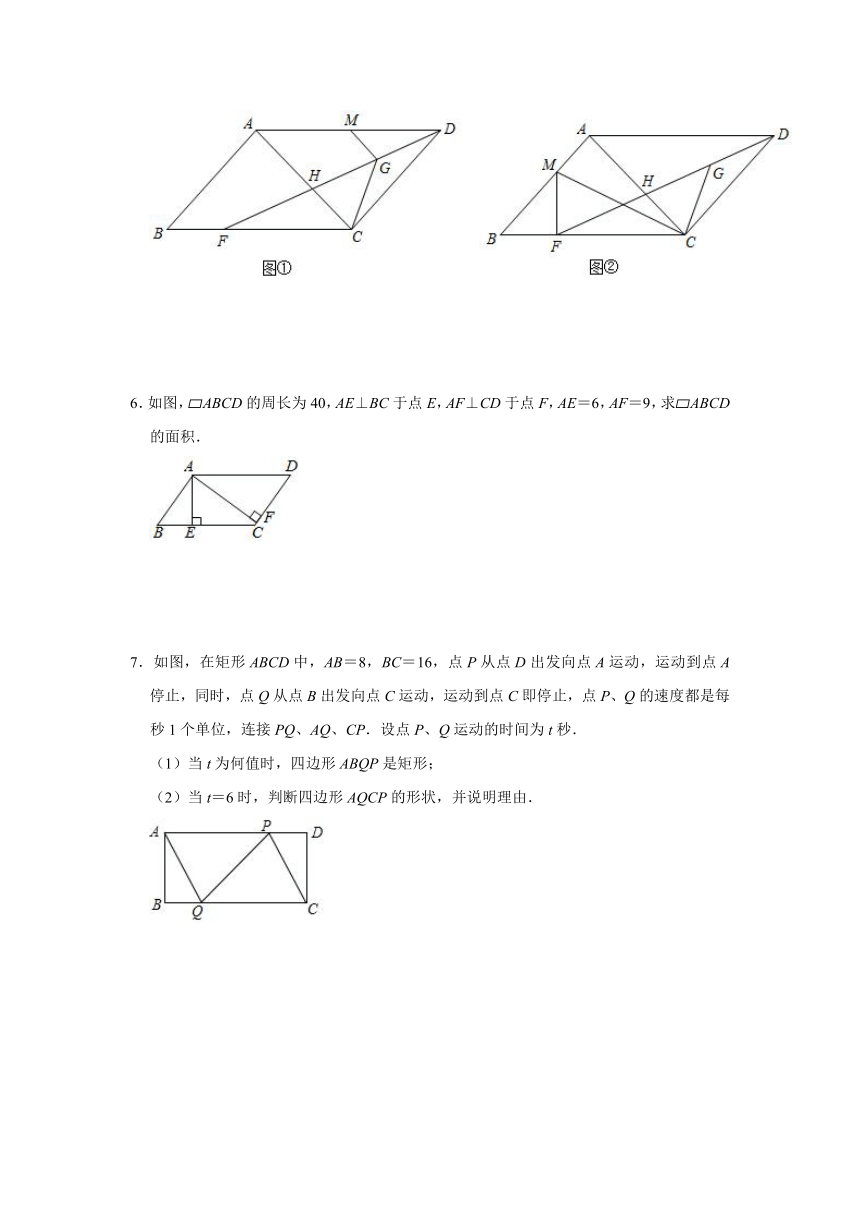
6.如图,?ABCD的周长为40,AE⊥BC于点E,AF⊥CD于点F,AE=6,AF=9,求?ABCD的面积.
7.如图,在矩形ABCD中,AB=8,BC=16,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是每秒1个单位,连接PQ、AQ、CP.设点P、Q运动的时间为t秒.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t=6时,判断四边形AQCP的形状,并说明理由.
8.如图,在?ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F,求证:DE=BF.
9.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF、DE.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=10,CF=6,直接写出DE的长为
.
10.如图,?ABCD中,∠ADC=120°,AD=AB,E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:DE=BE;
(2)请判断四边形AGBD是什么特殊的四边形,并说明理由.
11.如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F.AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=6,AD=9,∠ABC=60°,求∠DCP的度数及tan∠CDP的值.
12.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE∥DC,CE∥AB,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)如果∠B=60°,BC=2,求四边形AECD的面积.
13.如图,在△ABC中,∠BAC=90°,点D是BC中点,AE∥BC,CE∥AD.
(1)求证:四边形ADCE是菱形;
(2)过点D作DF⊥CE于点F,∠B=60°,AB=6,求EF的长.
14.如图,四边形ABCD中,∠BAD=∠BCD=90°,M、N分别为对角线BD、AC的中点,连接MN,判定MN与AC的位置关系并证明.
15.如图1,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.
参考答案
1.(1)证明:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=7时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=6,
∴BM=3,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=6,BC=AD=10,
∵AE=7,
∴DE=3=BM,
在△MBA和△EDC中,,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:7;
②当AE=4时,四边形CEDF是菱形,
理由是:∵AD=10,AE=4,
∴DE=6,
∵CD=6,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:4.
2.(1)证明:∵AE∥BC,∴∠EAO=∠DCO,
∵点O是AC中点,
∴OA=OC,
在△OAE和△OCD中,,
∴△OAE≌△OCD(ASA),
∴AE=CD,
∴四边形ADCE是平行四边形,
∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCE是矩形;
(2)解:四边形ABDE,四边形ADCE,△ABC,△BCE,理由如下:
由(1)得:四边形ADCE是矩形,
∴AD∥CE,△ACD的面积=△ACE的面积,
∴△ADE的面积=△ADF的面积,
∴四边形ABDE的面积=四边形ABDF的面积,
∵D是BC的中点,AE∥CD,
∴△BCE的面积=△ABC的面积=2△ACD的面积=2△ACE的面积,
∴△BCE的面积=△ABC的面积=四边形ADCE的面积=四边形ABDF的面积.
3.解:(1)由题意可得,a﹣2=0,2﹣b=0,
解得:a=2,b=2,
故答案为:2;2;
(2)过C作CH⊥OA于H,
∵∠BAC=90°,
∴∠OAB+∠CAH=90°,
∵∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠CAH=∠OBA,
∵AB=AC,
∴△AOB≌△CHA(AAS),
∴OB=AH=2,OA=CH=2,
∴C(2+2,2);
(3)设D(x,y),A(2,0),B(0,2),C(2+2,2),
以AD为对角线,可得:,
解得:,
∴D(2,2+2),
以AB为对角线,可得:,
解得:,
∴D(﹣2,2﹣2),
以AC为对角线,可得:,
解得:,
∴D(4+2,2﹣2),
∴D1(2,2+2),D2(﹣2,2﹣2),D3(4+2,2﹣2).
4.解:初步运用:在“平行四边形、矩形和菱形”这三种特殊的四边形中,一定是“完美四边形”的是矩形.
故答案为矩形、
问题探究:∵在完美四边形ABCD中,AD≠BC,∠B=60°,BD⊥DC,BC=6,
∴∠ABC=∠C=60°,∠DBC=∠ABD=30°,∠A=∠ADC=120°,
∴∠A+∠ABC=180°,
∴AD∥BC,四边形ABCD是等腰梯形,
∴AB=CD,
∴∠ADB=∠DBC=30°,
∴∠ABD=∠ADB,
∴AB=AD,
在Rt△BCD中,作DH⊥BC于H.
CD=BC=3,DH=,
∴四边形ABCD的周长为3+3+3+6=15,面积=×(3+6)×=.
应用拓展:①“完美四边形”有一组对边平行;
②完美四边形”有一组对边相等;
③完美四边形”的对角线相等;
5.解:(1)∵?ABCD,AB⊥AC,
∴∠BAC=∠ACD=90°,
∵G为DH的中点,
∴CG=HG=GD,
∵CG=2,
∴HD=4,
∵DF平分∠ADC,
∴∠DFC=∠ADF=∠CDF,
∴CF=CD,
∵CF=8,
∴CD=8,
在Rt△HCD中,HC=4,
∵AC=9,
∴AH=5,
∵M为AD的中点,
∴MG=AH=;
(2)如图②,过点D作DN∥AC,交CG的延长线于点N,
∴∠N=∠ACN,∠DAC=∠ADN,
∵G为DH的中点,
∴DG=HG,且∠N=∠ACG,∠CGH=∠DGN,
∴△CGH≌△NGD(AAS)
∴GC=GN,
∴CN=2CG,
∵∠MCD=∠BCG,
∴∠FCM=∠DCN,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠DAC=∠ACB=∠ADN,
∵∠MFB=∠BAC,∠B=∠B,且∠BMF=180°﹣∠B﹣∠BFM,∠ACB=180°﹣∠B﹣∠BAC,
∴∠BMF=∠ACB,
∴∠BMF=∠ADN,
∴∠BMF+∠B=∠ADN+∠ADC,
∴∠MFC=∠NDC,且CF=CD,∠FCM=∠DCN,
∴△MFC≌△NDC(ASA)
∴CM=CN,
∴CM=2CG.
6.解:∵?ABCD的周长=2(BC+CD)=40,
∴BC+CD=20①,
∵AE⊥BC于E,AF⊥CD于F,AE=6,AF=9,
∴S?ABCD=6BC=9CD,
整理得,BC=CD②,
联立①②解得,CD=8,
∴?ABCD的面积=AF?CD=9CD=9×8=72.
7.解:(1)∵在矩形ABCD中,AB=8,BC=16,
∴BC=AD=16,AB=CD=8,
由已知可得,BQ=DP=t,AP=CQ=16﹣t,
在矩形ABCD中,∠B=90°,AD∥BC,
当BQ=AP时,四边形ABQP为矩形,
∴t=16﹣t,
解得:t=8,
∴当t=8s时,四边形ABQP为矩形;
(2)四边形AQCP为菱形;理由如下:
∵t=6,
∴BQ=6,DP=6,
∴CQ=16﹣6=10,AP=16﹣6=10,
∴AP=CQ,AP∥CQ,
∴四边形AQCP为平行四边形,
在Rt△ABQ中,AQ===10,
∴AQ=CQ,
∴平行四边形AQCP为菱形,
即当t=6时,四边形AQCP为菱形.
8.证明:∵?ABCD的对角线AC,BD交于点O,
∴BO=DO,AD∥BC,
∴∠EDO=∠FBO,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA),
∴DE=BF.
9.解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点E,F分别为OA、OC的中点,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(SAS);
(2)∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∵BD=2AB,平行四边形ABCD中,对角线AC与BD交于点O,
∴AB=OB=OD=CD,
∵AB=10,CF=6,
∴AB=OB=OD=CD=10,AE=6,
∵AB=OB,点E、F分别为OA、OC的中点,
∴BE⊥AO,DF⊥CO,AE=CF=EO=OF=6,
∴DF=BE=8,EF=12,
在Rt△DEF中,
DE===4.
10.解:(1)证明:∵四边形ABCD是平行四边形,
∴在△ABD中,E是AB的中点,
∴AE=BE=AB,
∵AD=AB,
∴AD=AE,
∵∠ADC=120°,
∴∠DAB=60°
∴△AED是等边三角形,
∴DE=AE,
∴DE=BE;
(2)四边形AGBD是矩形,理由如下:
∵AD∥BC且AG∥DB,
∴四边形AGBD是平行四边形
由(1)的证明知AD=DE=AE=BE,
∴∠ADE=∠DEA=60°,
∴∠EDB=∠DBE=30°
∴∠ADB=90°
∴平行四边形AGBD是矩形.
11.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理:AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形;
(2)解:过P作PH⊥AD于H,交BC于G,如图所示:
则GH⊥BC,
∵四边形ABEF是菱形,∠ABC=60°,AB=6,
∴AB=AF=6,AE⊥BF,BP=FP,∠ABF=∠AFB=30°,
∴AP=AB=3,FP=BP=AP=3,
∴AH=AP=,PH=PF=,
∴DH=AD﹣AH=9﹣=,
∴PD===3,
同理:PG=PH=,BG=PG=,
∵四边形ABCD是平行四边形,
∴CD=AB=6,BC=AD=9,
∴CG=BC﹣BG=,
∴PC===3,
∵PC2+CD2=PD2,
∴△PCD是直角三角形,∠DCP=90°,
∴tan∠CDP===.
12.(1)证明:∵AE∥DC,CE∥AB,
∴四边形AECD是平行四边形,
∵Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD,
∴四边形AECD是菱形;
(2)解:连接DE.
∵∠ACB=90°,∠B=60°,
∴∠BAC=30°
∴AB=4,AC=2,
∵四边形AECD是菱形,
∴EC=AD=DB,
又∵EC∥DB
∴四边形ECBD是平行四边形,
∴ED=CB=2,
∴S菱形AECD=×AC×ED=2.
13.(1)证明:∵AE∥DC,EC∥AD,
∴四边形ADCE是平行四边形,
∵∠BAC=90°,点D是BC的中点,
∴AD=BD=CD,
∴平行四边形ADCE是菱形;
(2)解:∵∠B=60°,AD=BD,
∴△ABD是等边三角形,
∴∠ADB=60°,AD=AB=6,
∵AD∥CE,
∴∠DCE=60°,
∵CD=AD=6,
∴CF=CD=3,
∵四边形ADCE是菱形,
∴CE=CD=6,
∴EF=3.
14.解:MN⊥AC,
证明:连接AM,CM,
∵∠BAD=∠BCD=90°,M为BD的中点,
∴AM=,CM=BD,
∴AM=CM,
∵N为AC的中点,
∴MN⊥AC.
15.(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是平行四边形,
∴DC=AB.
∵OE=CD,
∴OE=AB.
∴平行四边形AEBO是矩形,
∴∠BOA=90°.
∴AC⊥BD.
∴平行四边形ABCD是菱形;
(2)解:由(1)得:四边形AEBO是矩形,四边形ABCD是菱形,
∴OA=BE=2,AC⊥BD,BO=DO,∠ADO=30°,
∴OD=OA=2,
∴BD=2OD=4.
解答题典型必练(三)
1.如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF为平行四边形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①当AE=
cm时,四边形CEDF是矩形;
②当AE=
cm时,四边形CEDF是菱形.
2.在△ABC中,AB=AC,点D、O分别是BC、AC边的中点,连接AD,过点A作AE∥BC,交射线DO于点E,连接CE.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,点F在线段CE上,连接AF、DF,在不添加任何字母和辅助线的情况下,请直接写出四个与四边形ABDF面积相等的三角形或四边形.
3.如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,顶点A(a,0),B(0,b)分别在x轴,y轴上,且满足.
(1)a=
,b=
;
(2)求点C的坐标;
(3)在平面直角坐标系中找一点D,使得点A,B,C,D组成的四边形为平行四边形.
4.我们定义:在四边形中,一条边上的两个角称为邻角,如果一条边上的邻角相等,且这条边对边上的邻角也相等,则把这样的四边形叫做“完美四边形”
初步运用:在“平行四边形、矩形和菱形”这三种特殊的四边形中,一定是“完美四边形”的是
.
问题探究:在完美四边形ABCD中,AD≠BC,∠B=60°,BD⊥DC,BC=6,求该完美四边形的周长与面积.
应用拓展:请你类比研究平行四边形及特殊四边形的方法,写出“完美四边形”的其中三条性质.
5.如图,?ABCD中,DF平分∠ADC交AC于点H,G为DH的中点.
(1)如图①,若M为AD的中点,AB⊥AC,AC=9,CF=8,CG=2,求GM;
(2)如图②,M为线段AB上一点,连接MF,满足∠MCD=∠BCG,∠MFB=∠BAC.求证:MC=2CG.
6.如图,?ABCD的周长为40,AE⊥BC于点E,AF⊥CD于点F,AE=6,AF=9,求?ABCD的面积.
7.如图,在矩形ABCD中,AB=8,BC=16,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是每秒1个单位,连接PQ、AQ、CP.设点P、Q运动的时间为t秒.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t=6时,判断四边形AQCP的形状,并说明理由.
8.如图,在?ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F,求证:DE=BF.
9.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF、DE.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=10,CF=6,直接写出DE的长为
.
10.如图,?ABCD中,∠ADC=120°,AD=AB,E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:DE=BE;
(2)请判断四边形AGBD是什么特殊的四边形,并说明理由.
11.如图,在?ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F.AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=6,AD=9,∠ABC=60°,求∠DCP的度数及tan∠CDP的值.
12.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,分别过点A,C作AE∥DC,CE∥AB,两线交于点E.
(1)求证:四边形AECD是菱形;
(2)如果∠B=60°,BC=2,求四边形AECD的面积.
13.如图,在△ABC中,∠BAC=90°,点D是BC中点,AE∥BC,CE∥AD.
(1)求证:四边形ADCE是菱形;
(2)过点D作DF⊥CE于点F,∠B=60°,AB=6,求EF的长.
14.如图,四边形ABCD中,∠BAD=∠BCD=90°,M、N分别为对角线BD、AC的中点,连接MN,判定MN与AC的位置关系并证明.
15.如图1,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.
参考答案
1.(1)证明:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=7时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=6,
∴BM=3,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=6,BC=AD=10,
∵AE=7,
∴DE=3=BM,
在△MBA和△EDC中,,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:7;
②当AE=4时,四边形CEDF是菱形,
理由是:∵AD=10,AE=4,
∴DE=6,
∵CD=6,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:4.
2.(1)证明:∵AE∥BC,∴∠EAO=∠DCO,
∵点O是AC中点,
∴OA=OC,
在△OAE和△OCD中,,
∴△OAE≌△OCD(ASA),
∴AE=CD,
∴四边形ADCE是平行四边形,
∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCE是矩形;
(2)解:四边形ABDE,四边形ADCE,△ABC,△BCE,理由如下:
由(1)得:四边形ADCE是矩形,
∴AD∥CE,△ACD的面积=△ACE的面积,
∴△ADE的面积=△ADF的面积,
∴四边形ABDE的面积=四边形ABDF的面积,
∵D是BC的中点,AE∥CD,
∴△BCE的面积=△ABC的面积=2△ACD的面积=2△ACE的面积,
∴△BCE的面积=△ABC的面积=四边形ADCE的面积=四边形ABDF的面积.
3.解:(1)由题意可得,a﹣2=0,2﹣b=0,
解得:a=2,b=2,
故答案为:2;2;
(2)过C作CH⊥OA于H,
∵∠BAC=90°,
∴∠OAB+∠CAH=90°,
∵∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠CAH=∠OBA,
∵AB=AC,
∴△AOB≌△CHA(AAS),
∴OB=AH=2,OA=CH=2,
∴C(2+2,2);
(3)设D(x,y),A(2,0),B(0,2),C(2+2,2),
以AD为对角线,可得:,
解得:,
∴D(2,2+2),
以AB为对角线,可得:,
解得:,
∴D(﹣2,2﹣2),
以AC为对角线,可得:,
解得:,
∴D(4+2,2﹣2),
∴D1(2,2+2),D2(﹣2,2﹣2),D3(4+2,2﹣2).
4.解:初步运用:在“平行四边形、矩形和菱形”这三种特殊的四边形中,一定是“完美四边形”的是矩形.
故答案为矩形、
问题探究:∵在完美四边形ABCD中,AD≠BC,∠B=60°,BD⊥DC,BC=6,
∴∠ABC=∠C=60°,∠DBC=∠ABD=30°,∠A=∠ADC=120°,
∴∠A+∠ABC=180°,
∴AD∥BC,四边形ABCD是等腰梯形,
∴AB=CD,
∴∠ADB=∠DBC=30°,
∴∠ABD=∠ADB,
∴AB=AD,
在Rt△BCD中,作DH⊥BC于H.
CD=BC=3,DH=,
∴四边形ABCD的周长为3+3+3+6=15,面积=×(3+6)×=.
应用拓展:①“完美四边形”有一组对边平行;
②完美四边形”有一组对边相等;
③完美四边形”的对角线相等;
5.解:(1)∵?ABCD,AB⊥AC,
∴∠BAC=∠ACD=90°,
∵G为DH的中点,
∴CG=HG=GD,
∵CG=2,
∴HD=4,
∵DF平分∠ADC,
∴∠DFC=∠ADF=∠CDF,
∴CF=CD,
∵CF=8,
∴CD=8,
在Rt△HCD中,HC=4,
∵AC=9,
∴AH=5,
∵M为AD的中点,
∴MG=AH=;
(2)如图②,过点D作DN∥AC,交CG的延长线于点N,
∴∠N=∠ACN,∠DAC=∠ADN,
∵G为DH的中点,
∴DG=HG,且∠N=∠ACG,∠CGH=∠DGN,
∴△CGH≌△NGD(AAS)
∴GC=GN,
∴CN=2CG,
∵∠MCD=∠BCG,
∴∠FCM=∠DCN,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠DAC=∠ACB=∠ADN,
∵∠MFB=∠BAC,∠B=∠B,且∠BMF=180°﹣∠B﹣∠BFM,∠ACB=180°﹣∠B﹣∠BAC,
∴∠BMF=∠ACB,
∴∠BMF=∠ADN,
∴∠BMF+∠B=∠ADN+∠ADC,
∴∠MFC=∠NDC,且CF=CD,∠FCM=∠DCN,
∴△MFC≌△NDC(ASA)
∴CM=CN,
∴CM=2CG.
6.解:∵?ABCD的周长=2(BC+CD)=40,
∴BC+CD=20①,
∵AE⊥BC于E,AF⊥CD于F,AE=6,AF=9,
∴S?ABCD=6BC=9CD,
整理得,BC=CD②,
联立①②解得,CD=8,
∴?ABCD的面积=AF?CD=9CD=9×8=72.
7.解:(1)∵在矩形ABCD中,AB=8,BC=16,
∴BC=AD=16,AB=CD=8,
由已知可得,BQ=DP=t,AP=CQ=16﹣t,
在矩形ABCD中,∠B=90°,AD∥BC,
当BQ=AP时,四边形ABQP为矩形,
∴t=16﹣t,
解得:t=8,
∴当t=8s时,四边形ABQP为矩形;
(2)四边形AQCP为菱形;理由如下:
∵t=6,
∴BQ=6,DP=6,
∴CQ=16﹣6=10,AP=16﹣6=10,
∴AP=CQ,AP∥CQ,
∴四边形AQCP为平行四边形,
在Rt△ABQ中,AQ===10,
∴AQ=CQ,
∴平行四边形AQCP为菱形,
即当t=6时,四边形AQCP为菱形.
8.证明:∵?ABCD的对角线AC,BD交于点O,
∴BO=DO,AD∥BC,
∴∠EDO=∠FBO,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA),
∴DE=BF.
9.解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点E,F分别为OA、OC的中点,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(SAS);
(2)∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∵BD=2AB,平行四边形ABCD中,对角线AC与BD交于点O,
∴AB=OB=OD=CD,
∵AB=10,CF=6,
∴AB=OB=OD=CD=10,AE=6,
∵AB=OB,点E、F分别为OA、OC的中点,
∴BE⊥AO,DF⊥CO,AE=CF=EO=OF=6,
∴DF=BE=8,EF=12,
在Rt△DEF中,
DE===4.
10.解:(1)证明:∵四边形ABCD是平行四边形,
∴在△ABD中,E是AB的中点,
∴AE=BE=AB,
∵AD=AB,
∴AD=AE,
∵∠ADC=120°,
∴∠DAB=60°
∴△AED是等边三角形,
∴DE=AE,
∴DE=BE;
(2)四边形AGBD是矩形,理由如下:
∵AD∥BC且AG∥DB,
∴四边形AGBD是平行四边形
由(1)的证明知AD=DE=AE=BE,
∴∠ADE=∠DEA=60°,
∴∠EDB=∠DBE=30°
∴∠ADB=90°
∴平行四边形AGBD是矩形.
11.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理:AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形;
(2)解:过P作PH⊥AD于H,交BC于G,如图所示:
则GH⊥BC,
∵四边形ABEF是菱形,∠ABC=60°,AB=6,
∴AB=AF=6,AE⊥BF,BP=FP,∠ABF=∠AFB=30°,
∴AP=AB=3,FP=BP=AP=3,
∴AH=AP=,PH=PF=,
∴DH=AD﹣AH=9﹣=,
∴PD===3,
同理:PG=PH=,BG=PG=,
∵四边形ABCD是平行四边形,
∴CD=AB=6,BC=AD=9,
∴CG=BC﹣BG=,
∴PC===3,
∵PC2+CD2=PD2,
∴△PCD是直角三角形,∠DCP=90°,
∴tan∠CDP===.
12.(1)证明:∵AE∥DC,CE∥AB,
∴四边形AECD是平行四边形,
∵Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD,
∴四边形AECD是菱形;
(2)解:连接DE.
∵∠ACB=90°,∠B=60°,
∴∠BAC=30°
∴AB=4,AC=2,
∵四边形AECD是菱形,
∴EC=AD=DB,
又∵EC∥DB
∴四边形ECBD是平行四边形,
∴ED=CB=2,
∴S菱形AECD=×AC×ED=2.
13.(1)证明:∵AE∥DC,EC∥AD,
∴四边形ADCE是平行四边形,
∵∠BAC=90°,点D是BC的中点,
∴AD=BD=CD,
∴平行四边形ADCE是菱形;
(2)解:∵∠B=60°,AD=BD,
∴△ABD是等边三角形,
∴∠ADB=60°,AD=AB=6,
∵AD∥CE,
∴∠DCE=60°,
∵CD=AD=6,
∴CF=CD=3,
∵四边形ADCE是菱形,
∴CE=CD=6,
∴EF=3.
14.解:MN⊥AC,
证明:连接AM,CM,
∵∠BAD=∠BCD=90°,M为BD的中点,
∴AM=,CM=BD,
∴AM=CM,
∵N为AC的中点,
∴MN⊥AC.
15.(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是平行四边形,
∴DC=AB.
∵OE=CD,
∴OE=AB.
∴平行四边形AEBO是矩形,
∴∠BOA=90°.
∴AC⊥BD.
∴平行四边形ABCD是菱形;
(2)解:由(1)得:四边形AEBO是矩形,四边形ABCD是菱形,
∴OA=BE=2,AC⊥BD,BO=DO,∠ADO=30°,
∴OD=OA=2,
∴BD=2OD=4.
