2020-2021苏科版八下 第九章 中心对称图形——平行四边形 解答题经典必练含答案(一)(word版含答案)
文档属性
| 名称 | 2020-2021苏科版八下 第九章 中心对称图形——平行四边形 解答题经典必练含答案(一)(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 166.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 10:07:02 | ||
图片预览


文档简介
第九章
中心对称图形——平行四边形
解答题经典必练(一)
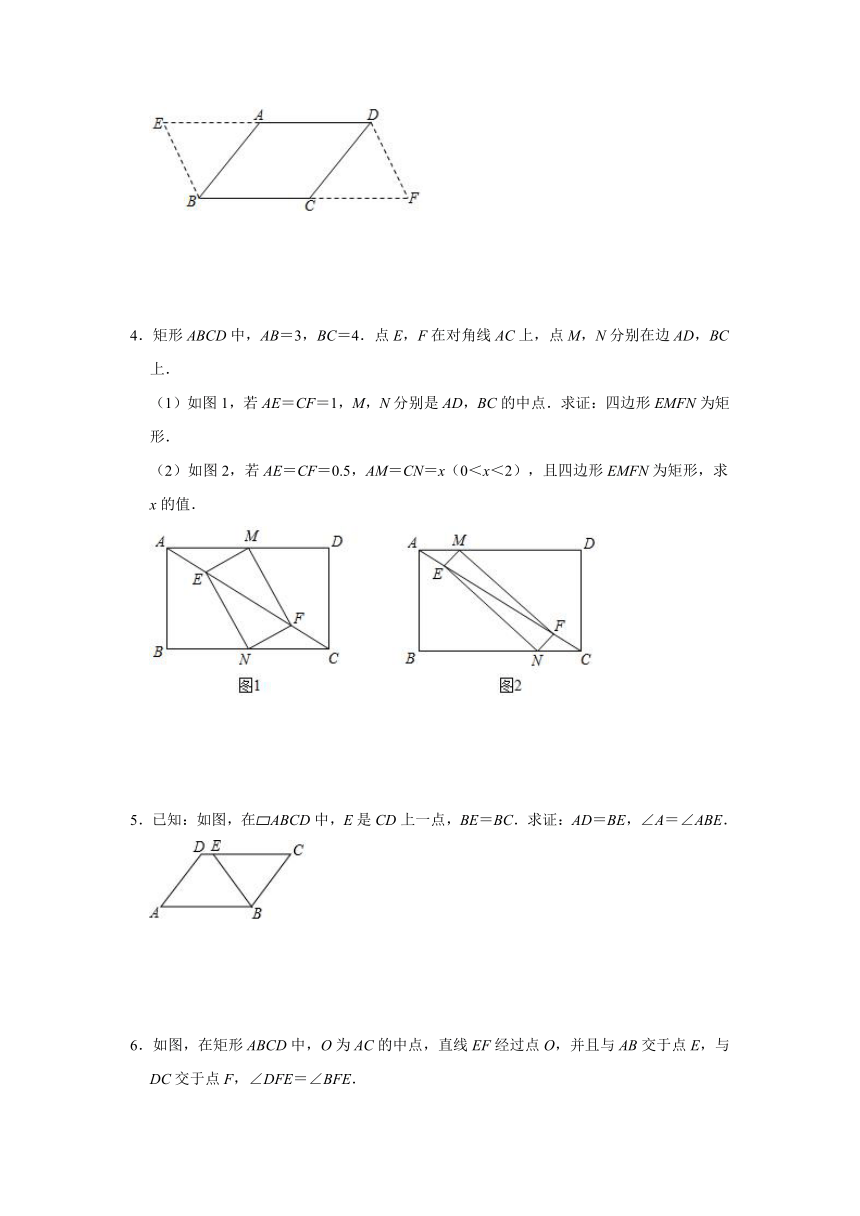
1.如图,在矩形ABCD中,对角线AC、BD相交于O,∠BOC=60°,E为AC上一点,连接BE,过点E作BE⊥EG交BD于G,且EG=BE,取BG中点H,连接EH.
(1)如图1,若OH=1,求线段AB的长;
(2)如图2,延长BC、HE相交于M,求证:HM+CM=DH.
2.已知:如图,在?ABCD中,点E在AB上,点F在CD上,且DE∥BF.
求证:BE=DF.
3.如图,在四边形ABCD中,AD∥BC,且AD+AB=BC+CD.证明四边形ABCD是平行四边形.
小明同学在证明该题时,他根据题目中条件“AD+AB=BC+CD”想到延长DA至E,使AE=AB,则DE=AD+AE=AD+AB;延长BC至F,使CF=CD,则BF=BC+CF=BC+CD,连接EB、DF.
请在小明想法的启示下完成并写出该问题证明的全过程.
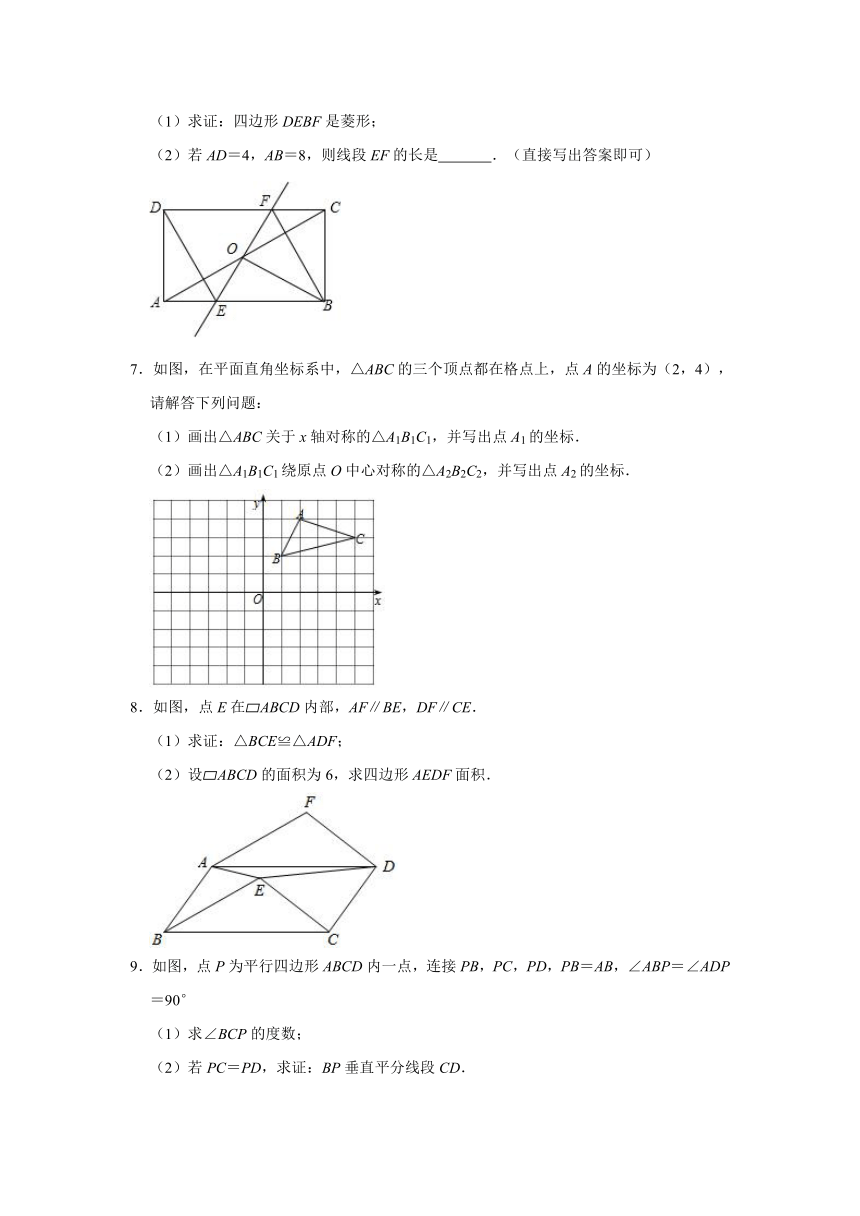
4.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.
(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.
(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x的值.
5.已知:如图,在?ABCD中,E是CD上一点,BE=BC.求证:AD=BE,∠A=∠ABE.
6.如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
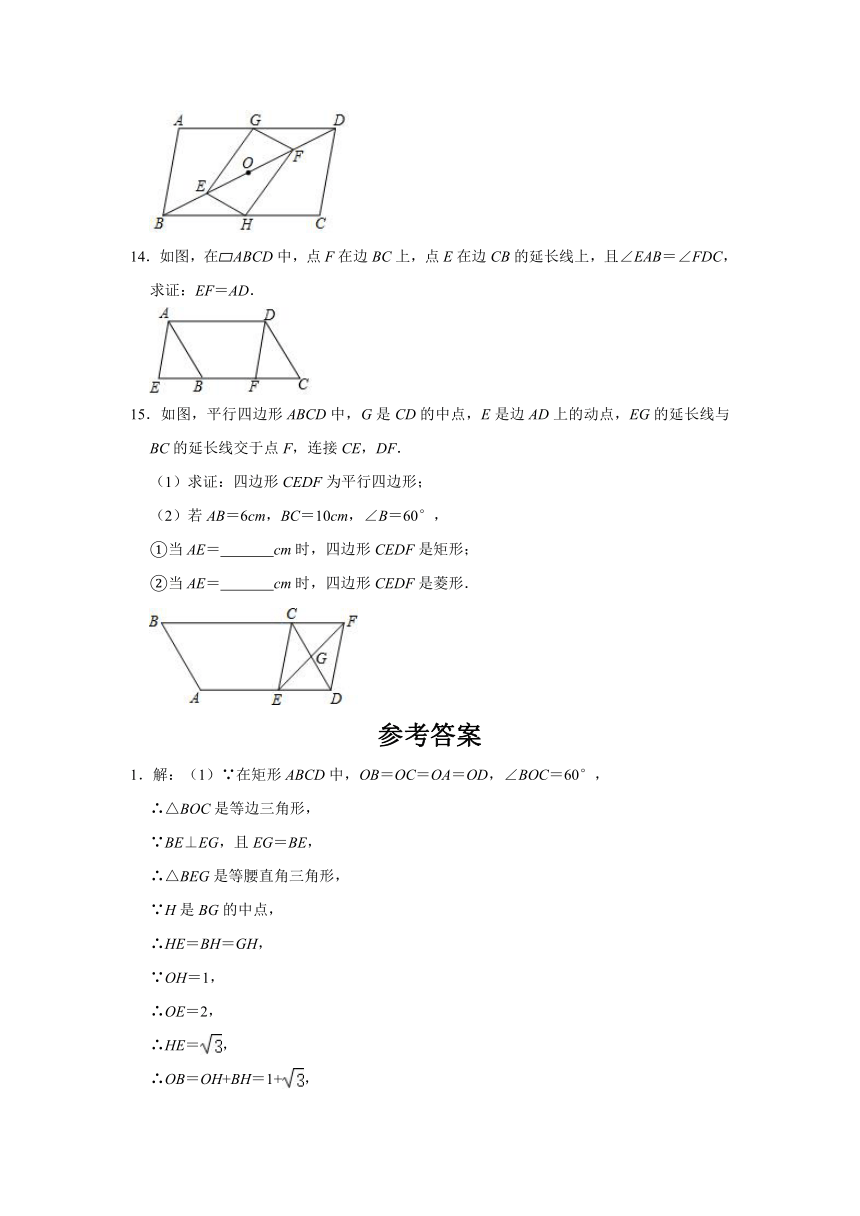
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是
.(直接写出答案即可)
7.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O中心对称的△A2B2C2,并写出点A2的坐标.
8.如图,点E在?ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF;
(2)设?ABCD的面积为6,求四边形AEDF面积.
9.如图,点P为平行四边形ABCD内一点,连接PB,PC,PD,PB=AB,∠ABP=∠ADP=90°
(1)求∠BCP的度数;
(2)若PC=PD,求证:BP垂直平分线段CD.
10.如图,AD是△ABC的中线,AE∥BC,且AE=BC,连接DE,CE.
(1)求证:AB=DE;
(2)当△ABC满足什么条件时,四边形ADCE是矩形?并说明理由.
11.如图,四边形ABCD是平行四边形对角线AC,BD交于点O,BD=2AB,AE∥BD,OE∥AB.
(1)求证:四边形ABOE是菱形;
(2)若AO=2,S四边形ABOE=4,求BD的长.
12.如图,在?ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
13.已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当平行四边形ABCD满足
条件时,四边形GEHF是菱形;
(3)若BD=2AB,探究四边形GEHF的形状,并说明理由.
14.如图,在?ABCD中,点F在边BC上,点E在边CB的延长线上,且∠EAB=∠FDC,求证:EF=AD.
15.如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF为平行四边形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①当AE=
cm时,四边形CEDF是矩形;
②当AE=
cm时,四边形CEDF是菱形.
参考答案
1.解:(1)∵在矩形ABCD中,OB=OC=OA=OD,∠BOC=60°,
∴△BOC是等边三角形,
∵BE⊥EG,且EG=BE,
∴△BEG是等腰直角三角形,
∵H是BG的中点,
∴HE=BH=GH,
∵OH=1,
∴OE=2,
∴HE=,
∴OB=OH+BH=1+,
∴AB=2×OB=3+;
(2)证明:∵∠CEM=∠OEH=30°,
∠OCB=60°,
∴∠M=30°,
∴CM=CE=OC﹣OE=OC﹣2OH,
∵△BEG是等腰直角三角形,H是BG的中点,
∴EH⊥BG,
∴HM=BH=(OB﹣OH),
设OH=x,
∴OE=2x,
∴HE=BH=x,
∴OB=OD=OH+BH=(1+)x,
∴DH=OD+OH=(1+)x+x=(2+)x,
∵HM+CM=(OB﹣OH)+OC﹣2OH
=(x+x﹣x)+x+x﹣2x
=2x+x
=(2+)x,
∴HM+CM=DH.
2.证明:∵四边形ABCD是平行四边形,
∴DC∥BA,
∴DF∥BE,
又∵DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
3.证明:法一:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AB=CD,
∵AD+AB=BC+CD,
∴AD=BC,
∴四边形ABCD是平行四边形.
法二:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠EAB=∠DCF,
又∵AD∥BC,
∴∠EAB=∠ABC,
∴∠ABC=∠DCF,
∴AB∥CD,
∴四边形ABCD为平行四边形.
4.(1)证明:连接MN,如图1所示:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=90°,
∴∠EAM=∠FCN,AC===5,
∵M,N分别是AD,BC的中点,
∴AM=DM=BN=CN,AM∥BN,
∴四边形ABNM是平行四边形,
又∵∠B=90°,
∴四边形ABNM是矩形,
∴MN=AB=3,
在△AME和△CNF中,,
∴△AME≌△CNF(SAS),
∴EM=FN,∠AEM=∠CFN,
∴∠MEF=∠NFE,
∴EM∥FN,
∴四边形EMFN是平行四边形,
又∵AE=CF=1,
∴EF=AC﹣AE﹣CF=3,
∴MN=EF,
∴四边形EMFN为矩形.
(2)解:连接MN,作MH⊥BC于H,如图2所示:
则四边形ABHM是矩形,
∴MH=AB=3,BH=AM=x,
∴HN=BC﹣BH﹣CN=4﹣2x,
∵四边形EMFN为矩形,AE=CF=0.5,
∴MN=EF=AC﹣AE﹣CF=4,
在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,
解得:x=2±,
∵0<x<2,
∴x=2﹣.
5.证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD=BC,
∴∠ABE=∠BEC,
∵BE=BC,
∴AD=BE,∠C=∠BEC,
∴∠A=∠ABE.
6.(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,DC=AB,
∴∠OAE=∠OCF,
∵OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
又∵∠DFE=∠BFE,∠DFE=∠FEB,
∴∠BFE=∠BEF,
∴BE=BF,
∴四边形DEBF是菱形.
(2)如图,作FH⊥AB于H.设DF=BF=x,
在Rt△BCF中,∠BCF=90°,BC=AD=4,CF=4﹣x,
∴x2=42+(8﹣x)2,
∴x=5,
∴DF=5,CF=3,
∵∠FHB=∠HBC=∠BCF=90°,
∴四边形BCFH是矩形,
∴CF=BH=3,FH=BC=4,
∵BF=DF=5,
∴EH=2,
∴EF===2,
故答案为.
7.解:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
8.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ABC+∠BAD=180°,
∵AF∥BE,
∴∠EBA+∠BAF=180°,
∴∠CBE=∠DAF,
同理得∠BCE=∠ADF,
在△BCE和△ADF中,
,
∴△BCE≌△ADF(ASA);
(2)解:∵点E在?ABCD内部,
∴S△BEC+S△AED=S?ABCD,
由(1)知:△BCE≌△ADF,
∴S△BCE=S△ADF,
∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=S?ABCD,
∵?ABCD的面积为6,
∴四边形AEDF的面积为3.
9.(1)解:如图:1,延长DP,交BC于点E.
在平行四边形ABCD中,AB=DC,∠A=∠BCD,∠ABC=∠ADC,
又∵PB=AB,
∴PB=CD.
∵∠ABP=∠ADP=90°,
∴∠A+∠BPD=180°,∠PBE=∠CDE.
又∵∠A=∠BCD,∠BPE+∠BPD=180°,
∴∠BPE=∠DCE,
在△BPE和△DCE中,,
∴△BPE≌△DCE(ASA),
∴∠BEP=∠DEC=90°,CE=EP,
∴∠BCP=45°.
(2)证明:连接BD,延长DP交BC于点E,如图2:
∵△BPE≌△DCE,
∴BE=DE,
则∠BDP=45°,
∴∠BDP=∠BCP.
∵PC=PD,
∴∠PCD=∠PDC,
∴∠BCD=∠BDC,
∴BD=BC.
又∵PC=PD,
∴BP垂直平分线段CD.
10.证明:(1)∵AD是△ABC的中线,
∴BD=CD=BC,
∵AE=BC,
∴AE=BD,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AB=DE;
(2)当△ABC满足AB=AC时,四边形ADCE是矩形,
∵AE=BC,BD=CD=BC,
∴AE=CD,
∵AE∥BC,
∴四边形ADCE是平行四边形,
∵AB=DE,
∴当AB=AC时,AC=DE,
∴四边形ADCE是矩形.
11.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD=BD,
∵BD=2AB,
∴AB=OB,
∵AE∥BD,OE∥AB,
∴四边形ABOE是平行四边形,
∵AB=OB,
∴四边形ABOE是菱形;
(2)解:连接BE,交OA于F,如图所示:
∵四边形ABOE是菱形,
∴OA⊥BE,AF=OF=OA=1,BF=EF=BE,
∵S四边形ABOE=4,
S四边形ABOE=OA?BE=×2×BE=BE,
∴BE=4,
∴BF=2,
∴OB===,
∴BD=2OB=2.
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形BEDF是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形BEDF是矩形.
13.(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,
∴E、F分别为OB、OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理:EH∥OC,EH=OC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形;
(2)解:当?ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:
则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB∥GH,
∵AB⊥BD,
∴GH⊥BD,
∴GH⊥EF,
∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,
∴GH=AB,
∵BD=2AB,
∴AB=BD=EF,
∴GH=EF,
∴四边形GEHF是矩形.
14.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠DCF,
在△ABE和△DCF中,
,
∴△BAE≌△CDF(ASA),
∴EF=AD.
15.(1)证明:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=7时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=6,
∴BM=3,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=6,BC=AD=10,
∵AE=7,
∴DE=3=BM,
在△MBA和△EDC中,,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:7;
②当AE=4时,四边形CEDF是菱形,
理由是:∵AD=10,AE=4,
∴DE=6,
∵CD=6,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:4.
中心对称图形——平行四边形
解答题经典必练(一)
1.如图,在矩形ABCD中,对角线AC、BD相交于O,∠BOC=60°,E为AC上一点,连接BE,过点E作BE⊥EG交BD于G,且EG=BE,取BG中点H,连接EH.
(1)如图1,若OH=1,求线段AB的长;
(2)如图2,延长BC、HE相交于M,求证:HM+CM=DH.
2.已知:如图,在?ABCD中,点E在AB上,点F在CD上,且DE∥BF.
求证:BE=DF.
3.如图,在四边形ABCD中,AD∥BC,且AD+AB=BC+CD.证明四边形ABCD是平行四边形.
小明同学在证明该题时,他根据题目中条件“AD+AB=BC+CD”想到延长DA至E,使AE=AB,则DE=AD+AE=AD+AB;延长BC至F,使CF=CD,则BF=BC+CF=BC+CD,连接EB、DF.
请在小明想法的启示下完成并写出该问题证明的全过程.
4.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.
(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.
(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x的值.
5.已知:如图,在?ABCD中,E是CD上一点,BE=BC.求证:AD=BE,∠A=∠ABE.
6.如图,在矩形ABCD中,O为AC的中点,直线EF经过点O,并且与AB交于点E,与DC交于点F,∠DFE=∠BFE.
(1)求证:四边形DEBF是菱形;
(2)若AD=4,AB=8,则线段EF的长是
.(直接写出答案即可)
7.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O中心对称的△A2B2C2,并写出点A2的坐标.
8.如图,点E在?ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF;
(2)设?ABCD的面积为6,求四边形AEDF面积.
9.如图,点P为平行四边形ABCD内一点,连接PB,PC,PD,PB=AB,∠ABP=∠ADP=90°
(1)求∠BCP的度数;
(2)若PC=PD,求证:BP垂直平分线段CD.
10.如图,AD是△ABC的中线,AE∥BC,且AE=BC,连接DE,CE.
(1)求证:AB=DE;
(2)当△ABC满足什么条件时,四边形ADCE是矩形?并说明理由.
11.如图,四边形ABCD是平行四边形对角线AC,BD交于点O,BD=2AB,AE∥BD,OE∥AB.
(1)求证:四边形ABOE是菱形;
(2)若AO=2,S四边形ABOE=4,求BD的长.
12.如图,在?ABCD中,BE⊥CD,点E为垂足,AF=CE,求证:四边形BEDF是矩形.
13.已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.
(1)求证:四边形GEHF是平行四边形;
(2)当平行四边形ABCD满足
条件时,四边形GEHF是菱形;
(3)若BD=2AB,探究四边形GEHF的形状,并说明理由.
14.如图,在?ABCD中,点F在边BC上,点E在边CB的延长线上,且∠EAB=∠FDC,求证:EF=AD.
15.如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.
(1)求证:四边形CEDF为平行四边形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①当AE=
cm时,四边形CEDF是矩形;
②当AE=
cm时,四边形CEDF是菱形.
参考答案
1.解:(1)∵在矩形ABCD中,OB=OC=OA=OD,∠BOC=60°,
∴△BOC是等边三角形,
∵BE⊥EG,且EG=BE,
∴△BEG是等腰直角三角形,
∵H是BG的中点,
∴HE=BH=GH,
∵OH=1,
∴OE=2,
∴HE=,
∴OB=OH+BH=1+,
∴AB=2×OB=3+;
(2)证明:∵∠CEM=∠OEH=30°,
∠OCB=60°,
∴∠M=30°,
∴CM=CE=OC﹣OE=OC﹣2OH,
∵△BEG是等腰直角三角形,H是BG的中点,
∴EH⊥BG,
∴HM=BH=(OB﹣OH),
设OH=x,
∴OE=2x,
∴HE=BH=x,
∴OB=OD=OH+BH=(1+)x,
∴DH=OD+OH=(1+)x+x=(2+)x,
∵HM+CM=(OB﹣OH)+OC﹣2OH
=(x+x﹣x)+x+x﹣2x
=2x+x
=(2+)x,
∴HM+CM=DH.
2.证明:∵四边形ABCD是平行四边形,
∴DC∥BA,
∴DF∥BE,
又∵DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
3.证明:法一:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(ASA),
∴AB=CD,
∵AD+AB=BC+CD,
∴AD=BC,
∴四边形ABCD是平行四边形.
法二:延长DA至E,使AE=AB,则DE=AD+AE=AD+AB.
延长BC至F,使CF=CD,则BF=BC+CF=BC+CD.
连接EB、DF.
∵AD+AB=BC+CD,
∴DE=BF,
又∵AD∥BC,
∴四边形DEBF为平行四边形,
∴EB=DF,∠E=∠F,
∵AB=AE,CD=CF,
∴∠ABE=∠E,∠CDF=∠F.
∴∠ABE=∠CDF,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(SAS),
∴∠EAB=∠DCF,
又∵AD∥BC,
∴∠EAB=∠ABC,
∴∠ABC=∠DCF,
∴AB∥CD,
∴四边形ABCD为平行四边形.
4.(1)证明:连接MN,如图1所示:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=90°,
∴∠EAM=∠FCN,AC===5,
∵M,N分别是AD,BC的中点,
∴AM=DM=BN=CN,AM∥BN,
∴四边形ABNM是平行四边形,
又∵∠B=90°,
∴四边形ABNM是矩形,
∴MN=AB=3,
在△AME和△CNF中,,
∴△AME≌△CNF(SAS),
∴EM=FN,∠AEM=∠CFN,
∴∠MEF=∠NFE,
∴EM∥FN,
∴四边形EMFN是平行四边形,
又∵AE=CF=1,
∴EF=AC﹣AE﹣CF=3,
∴MN=EF,
∴四边形EMFN为矩形.
(2)解:连接MN,作MH⊥BC于H,如图2所示:
则四边形ABHM是矩形,
∴MH=AB=3,BH=AM=x,
∴HN=BC﹣BH﹣CN=4﹣2x,
∵四边形EMFN为矩形,AE=CF=0.5,
∴MN=EF=AC﹣AE﹣CF=4,
在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,
解得:x=2±,
∵0<x<2,
∴x=2﹣.
5.证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,AD=BC,
∴∠ABE=∠BEC,
∵BE=BC,
∴AD=BE,∠C=∠BEC,
∴∠A=∠ABE.
6.(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,DC=AB,
∴∠OAE=∠OCF,
∵OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
又∵∠DFE=∠BFE,∠DFE=∠FEB,
∴∠BFE=∠BEF,
∴BE=BF,
∴四边形DEBF是菱形.
(2)如图,作FH⊥AB于H.设DF=BF=x,
在Rt△BCF中,∠BCF=90°,BC=AD=4,CF=4﹣x,
∴x2=42+(8﹣x)2,
∴x=5,
∴DF=5,CF=3,
∵∠FHB=∠HBC=∠BCF=90°,
∴四边形BCFH是矩形,
∴CF=BH=3,FH=BC=4,
∵BF=DF=5,
∴EH=2,
∴EF===2,
故答案为.
7.解:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
8.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ABC+∠BAD=180°,
∵AF∥BE,
∴∠EBA+∠BAF=180°,
∴∠CBE=∠DAF,
同理得∠BCE=∠ADF,
在△BCE和△ADF中,
,
∴△BCE≌△ADF(ASA);
(2)解:∵点E在?ABCD内部,
∴S△BEC+S△AED=S?ABCD,
由(1)知:△BCE≌△ADF,
∴S△BCE=S△ADF,
∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=S?ABCD,
∵?ABCD的面积为6,
∴四边形AEDF的面积为3.
9.(1)解:如图:1,延长DP,交BC于点E.
在平行四边形ABCD中,AB=DC,∠A=∠BCD,∠ABC=∠ADC,
又∵PB=AB,
∴PB=CD.
∵∠ABP=∠ADP=90°,
∴∠A+∠BPD=180°,∠PBE=∠CDE.
又∵∠A=∠BCD,∠BPE+∠BPD=180°,
∴∠BPE=∠DCE,
在△BPE和△DCE中,,
∴△BPE≌△DCE(ASA),
∴∠BEP=∠DEC=90°,CE=EP,
∴∠BCP=45°.
(2)证明:连接BD,延长DP交BC于点E,如图2:
∵△BPE≌△DCE,
∴BE=DE,
则∠BDP=45°,
∴∠BDP=∠BCP.
∵PC=PD,
∴∠PCD=∠PDC,
∴∠BCD=∠BDC,
∴BD=BC.
又∵PC=PD,
∴BP垂直平分线段CD.
10.证明:(1)∵AD是△ABC的中线,
∴BD=CD=BC,
∵AE=BC,
∴AE=BD,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AB=DE;
(2)当△ABC满足AB=AC时,四边形ADCE是矩形,
∵AE=BC,BD=CD=BC,
∴AE=CD,
∵AE∥BC,
∴四边形ADCE是平行四边形,
∵AB=DE,
∴当AB=AC时,AC=DE,
∴四边形ADCE是矩形.
11.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD=BD,
∵BD=2AB,
∴AB=OB,
∵AE∥BD,OE∥AB,
∴四边形ABOE是平行四边形,
∵AB=OB,
∴四边形ABOE是菱形;
(2)解:连接BE,交OA于F,如图所示:
∵四边形ABOE是菱形,
∴OA⊥BE,AF=OF=OA=1,BF=EF=BE,
∵S四边形ABOE=4,
S四边形ABOE=OA?BE=×2×BE=BE,
∴BE=4,
∴BF=2,
∴OB===,
∴BD=2OB=2.
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED.
∴四边形BEDF是平行四边形,
∵BE⊥CD,
∴∠BED=90°.
∴四边形BEDF是矩形.
13.(1)证明:连接AC,如图1所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴BD的中点在AC上,
∵E、O、F分别是对角线BD上的四等分点,
∴E、F分别为OB、OD的中点,
∵G是AD的中点,
∴GF为△AOD的中位线,
∴GF∥OA,GF=OA,
同理:EH∥OC,EH=OC,
∴EH=GF,EH∥GF,
∴四边形GEHF是平行四边形;
(2)解:当?ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:
连接GH,如图2所示:
则AG=BH,AG∥BH,
∴四边形ABHG是平行四边形,
∴AB∥GH,
∵AB⊥BD,
∴GH⊥BD,
∴GH⊥EF,
∴四边形GEHF是菱形;
故答案为:AB⊥BD;
(3)解:四边形GEHF是矩形;理由如下:
由(2)得:四边形GEHF是平行四边形,
∴GH=AB,
∵BD=2AB,
∴AB=BD=EF,
∴GH=EF,
∴四边形GEHF是矩形.
14.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠DCF,
在△ABE和△DCF中,
,
∴△BAE≌△CDF(ASA),
∴EF=AD.
15.(1)证明:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,
∴△CFG≌△EDG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=7时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=6,
∴BM=3,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=6,BC=AD=10,
∵AE=7,
∴DE=3=BM,
在△MBA和△EDC中,,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:7;
②当AE=4时,四边形CEDF是菱形,
理由是:∵AD=10,AE=4,
∴DE=6,
∵CD=6,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:4.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
