新人教版数学九年级上 直线与圆的位置关系
文档属性
| 名称 | 新人教版数学九年级上 直线与圆的位置关系 |  | |
| 格式 | zip | ||
| 文件大小 | 162.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-04 15:41:16 | ||
图片预览


文档简介
《直线和圆的位置关系》
课题 直线和圆的位置关系 理论依据或意图
教学目标 (1)知识目标: a、知道直线和圆相交、相切、相离的定义。 b、根据定义来判断直线和圆的位置关系,会根据直线和圆相切的定义画出已知圆的切线。 c、根据圆心到直线的距离与圆的半径之间的数量关系揭示直线和圆的位置。2)能力目标:a.培养学生通过观察“运动——变化”的过程来“分析——归纳” 获得新的知识;b.培养学生的自学能力,让学生独立思考和判断,来提高学生的判断能力。 3)情感目标: 在教学过程中,培养学生团结协作的精神。让学生在获得知识的同时,感受到学习的乐趣,鼓励学生大胆猜测,培养学生的独立个性和创新意识。 根据《教学大纲》和素质教育的要求,结合教育新理念和学生的认识规律和实际水平。
教学重点 直线和圆的位置的关系判定方法和性质。解决重点的方法主要是:(1)由学生观察老师展示的一轮红日从海平面升起的照片提出问题,能不能我们学过的知识把它们抽象出几何图形再展示出来(让学生尝试通过日出的情境画出几种情况),(2)把直线在圆的上下移动,引导学生用运动的观点观察直线和圆的位置关系,并让他们发现直线与圆的公共点的个数,揭示直线和圆相交、相切、相离的定义,归纳直线和圆的三种位置关系。是什么?)。 这是因为学生通过观察直线和圆的相对运动,引出直线和圆的三种位置关系.使学生从运动的观点,量变到质变的观点,来理解直线和圆相交、相切、相离的概念,结合图形直观地得圆心到直线的距离d与圆的半径r的数量关系.
教学难点 直线和圆三种位置关系的研究与运用。在说直线与圆的位置关系时,如何突破这个难点:(1)突破直线和圆不能有两个以上的公共点,让学生讨论,最后明确否定(因为直线和圆有三个或三个以上的公共点,那么这与不在同一条直线上的三点就可以作一个圆,相矛盾)。(2)把直线在圆的上下移动,引导学生用运动的观点观察直线和圆的位置关系,并让他们发现直线与圆的公共点的个数,揭示直线和圆相交、相切、相离的定义,归纳直线和圆的三种位置关系。(3)突破直线和圆有唯一一个公共点是直线和圆相切(指直线与圆有一个并且只有一个公共点,它与有一个公共点的含义不同)。(4)突破直线和圆的位置关系的(如果圆O的半径为r,圆心到直线的距离为d,1,直线l与圆 O相交 <=> d d=r 3,直线l与圆 O相离 <=> d>r(上述结论中的符号“<=> ”读作“等价于”)式子的左边反映是两个图形(直线和圆)的位置关系的性质,右边是反映直线和圆的位置关系的判定。 因为学生要根据圆心到直线的距离与半径的比较,来判定直线和圆的位置关系。这是数量关系和图形关系相结合。
教学方法 教 法 分 析 本节课采取启发式,通过谈话交流的方式进行教学,引导学生观察直线和圆的相对运动过程。经过讨论、分析、归纳,概括出直线和圆的三种位置关系:相交、相切、相离。并且明确“圆心到直线的距离d和半径r的数量关系”这一性质。使学生会根据这一性质来判定直线和圆的位置关系。从而达到既突出了本节课的重点又突破了难点的目标。 在教学手段上,采用“课件”进行辅助教学,能有效地突破难点,提高教学效果。
学 法 指 导 复习点和圆的位置关系,引导学生用类比的方法来研究直线与圆的位置关系,在直线与圆的位置关系的判定的过程中,采用小组讨论的方法,培养学生互助、协作的精神。学生质疑这一环节充分培养学生敢于提问的习惯,做到不懂就问。学生小结,让学生自己归纳本节课学习的内容,培养学生用数学语言归纳问题的能力。 通过观察演示,让每一个学生都能动口、动手、动脑,积极思考,勇于探索,培养学生的主动性和创造性。
教学环节 教 学 活 动 教学简析
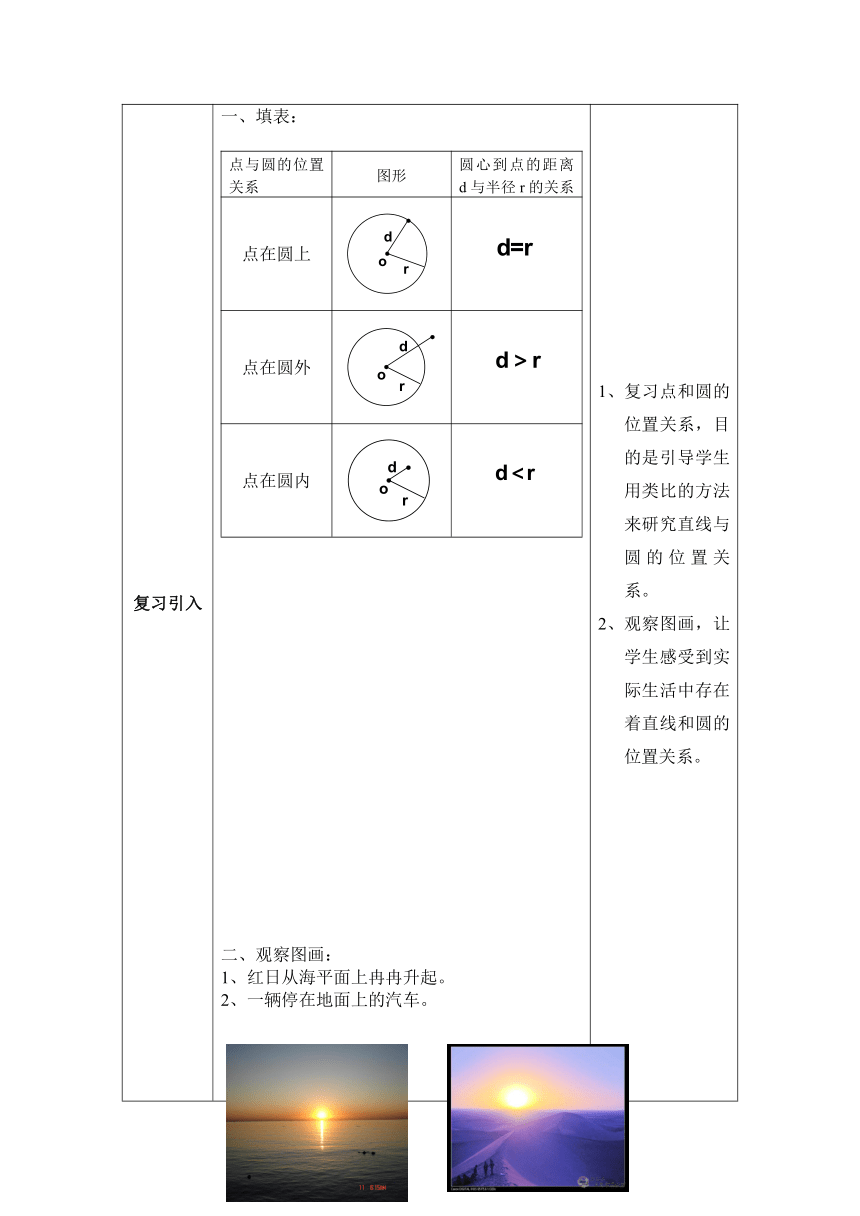
复习引入 填表:点与圆的位置关系图形圆心到点的距离d与半径r的关系点在圆上点在圆外点在圆内二、观察图画:1、红日从海平面上冉冉升起。2、一辆停在地面上的汽车。 复习点和圆的位置关系,目的是引导学生用类比的方法来研究直线与圆的位置关系。观察图画,让学生感受到实际生活中存在着直线和圆的位置关系。
实验探究 画图并实验:画一个圆O,用一根竹针当直线,并在纸面上任意移动。二、思考下列问题:观察直线和圆的公共点有几个?观察直线和圆的位置关系有几种?这几种关系分别是怎样定义?相交:直线和圆有两个公共点时,叫做直线和圆相交。相切:直线和圆有唯一公共点时,叫做直线和圆相切。相离:直线和圆没有公共点时,叫做直线和圆相离。三、提出问题:点和圆的的位置关系是由圆心到点的距离d与圆的半径r的关系来判定,那么直线与圆的位置关系又由什么量来判断呢?四、实验探讨:学生准备一个圆、一根竹针、一根橡皮筋、把橡皮筋一端固定在圆心,一端附着在竹针上,用橡皮筋的长表示圆心到直线的距离,竹针表示直线,移动竹针,让学生观察直线与圆在三种不同的位置时,橡皮筋的长与圆的半径的大小关系。 便于学生观察直线与圆的公共点的个数,便于学生用运动的观点观察圆与直线的位置关系。学生动手做实验,培养学生的动手操作的能力。让学生自己作出判断,并概括和叙述,有利于提高学生的语言表述能力。强化切线的定义,要让学生理解“唯一”即“有一个且只有一个”的意思。提出问题,让学生思考。运用类比的方法,通过学生做实验,合作探讨,得出判定直线和圆的位置关系的数量关系。老师再通过演示,更好地说明决定直线和圆的位置关系的关键所在。
知识反馈 一、已知⊙O的直径为12cm.1、若圆心O到直线l的距离为12cm,则直线l与⊙O 的位置关系为________;2、若圆心O到直线l的距离为6cm,则直线l与⊙O 的位置关系为________;3、若圆心O到直线l的距离为3cm,则直线l与 ⊙O 的位置关系为________.二、已知⊙O的直径为10cm.1、若直线l与⊙O相交,则圆心O到直线l的距离d ________;2、若直线l与⊙O相切,则圆心O到直线l的距离d ________;3、若直线l与⊙O相离,则圆心O到直线l的距离d ________. 1、该练习加深学生对概念的理解与掌握。2、学生完成后提问,老师小结。
技能应用 例:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,(1)、以C为圆心,半径r=2cm的圆与AB有怎样的位置关系?为什么?(2)、以C为圆心,半径r=2.4cm的圆与AB有怎样的位置关系?为什么?(3)、以C为圆心,半径r=3cm的圆与AB有怎样的位置关系?为什么? 引导学生去探究:决定直线和圆的位置关系的关键是什么?从而得出关键是把圆心C到AB的距离d求出来,即Rt△ABC斜边上的高。为此可用面积法计算,让学生独立作出解答。
巩固练习 如图:已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样位置关系?为什么?r =2cmr =4cmr =2.5cm 判断直线和圆的位置关系的关键是圆的半径r与点M到OA的距离进行比较。
小结 1、直线和圆的位置关系表:直线和圆的位置关系相交相切相离公共点的个数210公共点名称交点切点圆心到直线的距离d与r的关系d<rd=rd>r直线名称割线切线2、本节课从运动变化观点研究直线和圆的位置关系,通过点与圆的位置关系的类比,利用分类和数形结合的思想,得到了直线和圆的位置关系的判断和性质。 教师引导,学生进行总结。
板书设计 直线和圆的位置关系三种: 直线和圆相交直线和圆相切直线和圆相离性质:①直线和圆相交 d < r;②直线和圆相切 d = r;③直线和圆相离 d > r; 整洁有序的板书设计有利于学生对本节课的知识有一个系统的认识;同时可以培养学生的条理性和整洁的习惯。
课后作业 课本:P100 第2、3题思考:直线与圆的位置关系有哪几种区分方法? 思考题的目的是培养学生总结问题的能力。
相离 d>r
相切 d=r
相交 d<r
课题 直线和圆的位置关系 理论依据或意图
教学目标 (1)知识目标: a、知道直线和圆相交、相切、相离的定义。 b、根据定义来判断直线和圆的位置关系,会根据直线和圆相切的定义画出已知圆的切线。 c、根据圆心到直线的距离与圆的半径之间的数量关系揭示直线和圆的位置。2)能力目标:a.培养学生通过观察“运动——变化”的过程来“分析——归纳” 获得新的知识;b.培养学生的自学能力,让学生独立思考和判断,来提高学生的判断能力。 3)情感目标: 在教学过程中,培养学生团结协作的精神。让学生在获得知识的同时,感受到学习的乐趣,鼓励学生大胆猜测,培养学生的独立个性和创新意识。 根据《教学大纲》和素质教育的要求,结合教育新理念和学生的认识规律和实际水平。
教学重点 直线和圆的位置的关系判定方法和性质。解决重点的方法主要是:(1)由学生观察老师展示的一轮红日从海平面升起的照片提出问题,能不能我们学过的知识把它们抽象出几何图形再展示出来(让学生尝试通过日出的情境画出几种情况),(2)把直线在圆的上下移动,引导学生用运动的观点观察直线和圆的位置关系,并让他们发现直线与圆的公共点的个数,揭示直线和圆相交、相切、相离的定义,归纳直线和圆的三种位置关系。是什么?)。 这是因为学生通过观察直线和圆的相对运动,引出直线和圆的三种位置关系.使学生从运动的观点,量变到质变的观点,来理解直线和圆相交、相切、相离的概念,结合图形直观地得圆心到直线的距离d与圆的半径r的数量关系.
教学难点 直线和圆三种位置关系的研究与运用。在说直线与圆的位置关系时,如何突破这个难点:(1)突破直线和圆不能有两个以上的公共点,让学生讨论,最后明确否定(因为直线和圆有三个或三个以上的公共点,那么这与不在同一条直线上的三点就可以作一个圆,相矛盾)。(2)把直线在圆的上下移动,引导学生用运动的观点观察直线和圆的位置关系,并让他们发现直线与圆的公共点的个数,揭示直线和圆相交、相切、相离的定义,归纳直线和圆的三种位置关系。(3)突破直线和圆有唯一一个公共点是直线和圆相切(指直线与圆有一个并且只有一个公共点,它与有一个公共点的含义不同)。(4)突破直线和圆的位置关系的(如果圆O的半径为r,圆心到直线的距离为d,1,直线l与圆 O相交 <=> d
教学方法 教 法 分 析 本节课采取启发式,通过谈话交流的方式进行教学,引导学生观察直线和圆的相对运动过程。经过讨论、分析、归纳,概括出直线和圆的三种位置关系:相交、相切、相离。并且明确“圆心到直线的距离d和半径r的数量关系”这一性质。使学生会根据这一性质来判定直线和圆的位置关系。从而达到既突出了本节课的重点又突破了难点的目标。 在教学手段上,采用“课件”进行辅助教学,能有效地突破难点,提高教学效果。
学 法 指 导 复习点和圆的位置关系,引导学生用类比的方法来研究直线与圆的位置关系,在直线与圆的位置关系的判定的过程中,采用小组讨论的方法,培养学生互助、协作的精神。学生质疑这一环节充分培养学生敢于提问的习惯,做到不懂就问。学生小结,让学生自己归纳本节课学习的内容,培养学生用数学语言归纳问题的能力。 通过观察演示,让每一个学生都能动口、动手、动脑,积极思考,勇于探索,培养学生的主动性和创造性。
教学环节 教 学 活 动 教学简析
复习引入 填表:点与圆的位置关系图形圆心到点的距离d与半径r的关系点在圆上点在圆外点在圆内二、观察图画:1、红日从海平面上冉冉升起。2、一辆停在地面上的汽车。 复习点和圆的位置关系,目的是引导学生用类比的方法来研究直线与圆的位置关系。观察图画,让学生感受到实际生活中存在着直线和圆的位置关系。
实验探究 画图并实验:画一个圆O,用一根竹针当直线,并在纸面上任意移动。二、思考下列问题:观察直线和圆的公共点有几个?观察直线和圆的位置关系有几种?这几种关系分别是怎样定义?相交:直线和圆有两个公共点时,叫做直线和圆相交。相切:直线和圆有唯一公共点时,叫做直线和圆相切。相离:直线和圆没有公共点时,叫做直线和圆相离。三、提出问题:点和圆的的位置关系是由圆心到点的距离d与圆的半径r的关系来判定,那么直线与圆的位置关系又由什么量来判断呢?四、实验探讨:学生准备一个圆、一根竹针、一根橡皮筋、把橡皮筋一端固定在圆心,一端附着在竹针上,用橡皮筋的长表示圆心到直线的距离,竹针表示直线,移动竹针,让学生观察直线与圆在三种不同的位置时,橡皮筋的长与圆的半径的大小关系。 便于学生观察直线与圆的公共点的个数,便于学生用运动的观点观察圆与直线的位置关系。学生动手做实验,培养学生的动手操作的能力。让学生自己作出判断,并概括和叙述,有利于提高学生的语言表述能力。强化切线的定义,要让学生理解“唯一”即“有一个且只有一个”的意思。提出问题,让学生思考。运用类比的方法,通过学生做实验,合作探讨,得出判定直线和圆的位置关系的数量关系。老师再通过演示,更好地说明决定直线和圆的位置关系的关键所在。
知识反馈 一、已知⊙O的直径为12cm.1、若圆心O到直线l的距离为12cm,则直线l与⊙O 的位置关系为________;2、若圆心O到直线l的距离为6cm,则直线l与⊙O 的位置关系为________;3、若圆心O到直线l的距离为3cm,则直线l与 ⊙O 的位置关系为________.二、已知⊙O的直径为10cm.1、若直线l与⊙O相交,则圆心O到直线l的距离d ________;2、若直线l与⊙O相切,则圆心O到直线l的距离d ________;3、若直线l与⊙O相离,则圆心O到直线l的距离d ________. 1、该练习加深学生对概念的理解与掌握。2、学生完成后提问,老师小结。
技能应用 例:在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,(1)、以C为圆心,半径r=2cm的圆与AB有怎样的位置关系?为什么?(2)、以C为圆心,半径r=2.4cm的圆与AB有怎样的位置关系?为什么?(3)、以C为圆心,半径r=3cm的圆与AB有怎样的位置关系?为什么? 引导学生去探究:决定直线和圆的位置关系的关键是什么?从而得出关键是把圆心C到AB的距离d求出来,即Rt△ABC斜边上的高。为此可用面积法计算,让学生独立作出解答。
巩固练习 如图:已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样位置关系?为什么?r =2cmr =4cmr =2.5cm 判断直线和圆的位置关系的关键是圆的半径r与点M到OA的距离进行比较。
小结 1、直线和圆的位置关系表:直线和圆的位置关系相交相切相离公共点的个数210公共点名称交点切点圆心到直线的距离d与r的关系d<rd=rd>r直线名称割线切线2、本节课从运动变化观点研究直线和圆的位置关系,通过点与圆的位置关系的类比,利用分类和数形结合的思想,得到了直线和圆的位置关系的判断和性质。 教师引导,学生进行总结。
板书设计 直线和圆的位置关系三种: 直线和圆相交直线和圆相切直线和圆相离性质:①直线和圆相交 d < r;②直线和圆相切 d = r;③直线和圆相离 d > r; 整洁有序的板书设计有利于学生对本节课的知识有一个系统的认识;同时可以培养学生的条理性和整洁的习惯。
课后作业 课本:P100 第2、3题思考:直线与圆的位置关系有哪几种区分方法? 思考题的目的是培养学生总结问题的能力。
相离 d>r
相切 d=r
相交 d<r
同课章节目录
