24.2与圆有关的位置关系
文档属性
| 名称 | 24.2与圆有关的位置关系 | 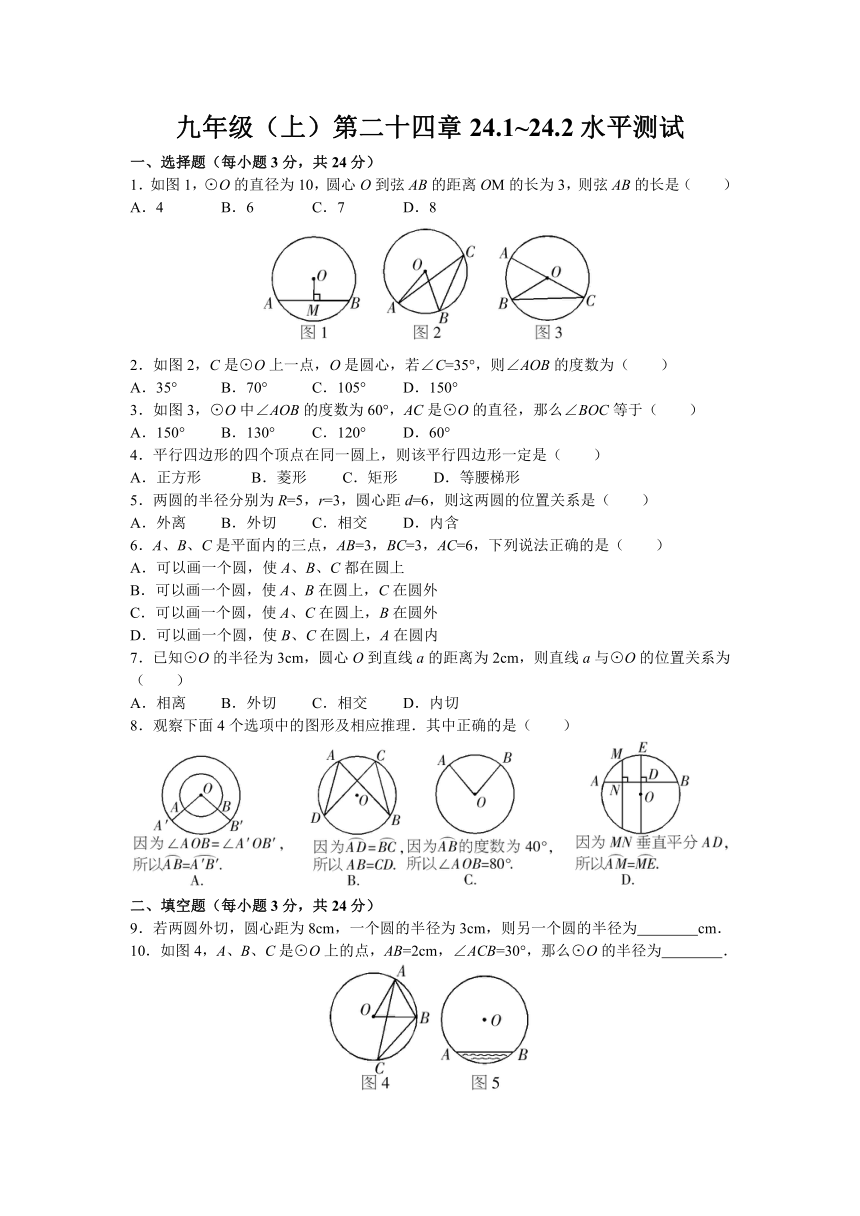 | |
| 格式 | zip | ||
| 文件大小 | 89.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-04 20:34:07 | ||
图片预览

文档简介
九年级(上)第二十四章24.1~24.2水平测试
一、选择题(每小题3分,共24分)
1.如图1,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是( )
A.4 B.6 C.7 D.8
2.如图2,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
A.35° B.70° C.105° D.150°
3.如图3,⊙O中∠AOB的度数为60°,AC是⊙O的直径,那么∠BOC等于( )
A.150° B.130° C.120° D.60°
4.平行四边形的四个顶点在同一圆上,则该平行四边形一定是( )
A.正方形 B.菱形 C.矩形 D.等腰梯形
5.两圆的半径分别为R=5,r=3,圆心距d=6,则这两圆的位置关系是( )
A.外离 B.外切 C.相交 D.内含
6.A、B、C是平面内的三点,AB=3,BC=3,AC=6,下列说法正确的是( )
A.可以画一个圆,使A、B、C都在圆上
B.可以画一个圆,使A、B在圆上,C在圆外
C.可以画一个圆,使A、C在圆上,B在圆外
D.可以画一个圆,使B、C在圆上,A在圆内
7.已知⊙O的半径为3cm,圆心O到直线a的距离为2cm,则直线a与⊙O的位置关系为( )
A.相离 B.外切 C.相交 D.内切
8.观察下面4个选项中的图形及相应推理.其中正确的是( )
二、填空题(每小题3分,共24分)
9.若两圆外切,圆心距为8cm,一个圆的半径为3cm,则另一个圆的半径为 cm.
10.如图4,A、B、C是⊙O上的点,AB=2cm,∠ACB=30°,那么⊙O的半径为 .
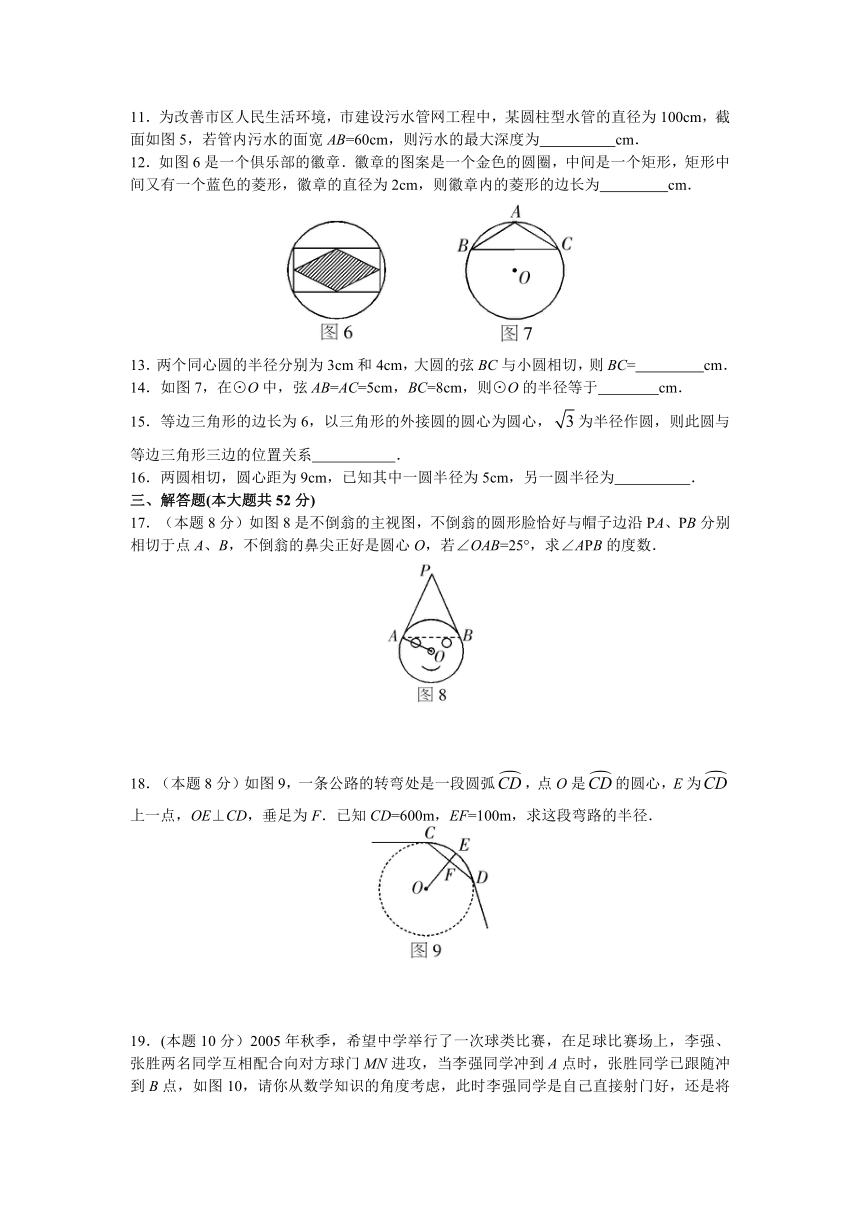
11.为改善市区人民生活环境,市建设污水管网工程中,某圆柱型水管的直径为100cm,截面如图5,若管内污水的面宽AB=60cm,则污水的最大深度为 cm.
12.如图6是一个俱乐部的徽章.徽章的图案是一个金色的圆圈,中间是一个矩形,矩形中间又有一个蓝色的菱形,徽章的直径为2cm,则徽章内的菱形的边长为 cm.
13.两个同心圆的半径分别为3cm和4cm,大圆的弦BC与小圆相切,则BC= cm.
14.如图7,在⊙O中,弦AB=AC=5cm,BC=8cm,则⊙O的半径等于 cm.
15.等边三角形的边长为6,以三角形的外接圆的圆心为圆心,为半径作圆,则此圆与等边三角形三边的位置关系 .
16.两圆相切,圆心距为9cm,已知其中一圆半径为5cm,另一圆半径为 .
三、解答题(本大题共52分)
17.(本题8分)如图8是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数.
18.(本题8分)如图9,一条公路的转弯处是一段圆弧,点O是的圆心,E为上一点,OE⊥CD,垂足为F.已知CD=600m,EF=100m,求这段弯路的半径.
19.(本题10分)2005年秋季,希望中学举行了一次球类比赛,在足球比赛场上,李强、张胜两名同学互相配合向对方球门MN进攻,当李强同学冲到A点时,张胜同学已跟随冲到B点,如图10,请你从数学知识的角度考虑,此时李强同学是自己直接射门好,还是将球传给张胜同学,让张胜同学射门好,简述理由.
20.(本题12分)如图11,AB为⊙O的直径,C是⊙O上的一点,D在AB的延长线上,且∠DCB=∠A,
(1)CD与⊙O相切吗 如果相切,请你加以证明;如果不相切,请说明理由.
(2)若∠D=30°,BD=10cm.求⊙O的半径.
21.(本题14分)在同一平面内,已知点O到直线l的距离为5,以点O为圆心,r为半径画圆.探究、归纳:
(1)当r= 时,⊙O上有且只有一个点到直线l的距离等于3.
(2)当r= 时,⊙O上有且只有三个点到直线l的距离等于3.
(3)随着r的变化,⊙O上到直线l的距离等于3的点的个数有哪些变化?并求出相对应的r的值或取值范围(不必写出计算过程).
附加题(本题20分,不计入总分)
22.拓广探究:如图12,AB是⊙O的直径,C为圆周上一点,BD是⊙O的切线,B为切点.
(1)在图12(1)中,∠BAC=30°,求∠DBC的度数;
(2)在图12(2)中,∠BA1C=40°,求∠DBC的度数.
(3)在图12(3)中,∠BA1C=α,求∠DBC大小.
(4)通过(1)、(2)、(3)的探究,你发现了什么?用自己的语言叙述你的发现.
参考答案:
一、1~5.DBCCC 6~8.BCB
二、9.5 10.2cm 11.10 12.1 13.
14. 15.相切 16.4cm或14cm
三、17..
18.这段弯路的半径为500米.
19.李强把球转给张胜同学射门较好.理由略.
20.(1)相切,证明略.
(2)10cm.
21.(1)2;(2)8;
(3)当时,上没有点到直线的距离等于3.
当时,上有且只有1个点到直线的距离等于3.
当时,上有且只有2个点到直线的距离等于3.
当时,上有且只有3个点到直线的距离等于3.
当时,上有且只有4个点到直线的距离等于3.
附加题:
22.(1).
(2)连接,根据(1)可得.
(3)连接,根据(1)可得.
(4)在图(1)中,,在图(2),图(3),中,由此可得:圆的切线与弦所成的角等于它所夹的弧所对的圆周角.
一、选择题(每小题3分,共24分)
1.如图1,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是( )
A.4 B.6 C.7 D.8
2.如图2,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
A.35° B.70° C.105° D.150°
3.如图3,⊙O中∠AOB的度数为60°,AC是⊙O的直径,那么∠BOC等于( )
A.150° B.130° C.120° D.60°
4.平行四边形的四个顶点在同一圆上,则该平行四边形一定是( )
A.正方形 B.菱形 C.矩形 D.等腰梯形
5.两圆的半径分别为R=5,r=3,圆心距d=6,则这两圆的位置关系是( )
A.外离 B.外切 C.相交 D.内含
6.A、B、C是平面内的三点,AB=3,BC=3,AC=6,下列说法正确的是( )
A.可以画一个圆,使A、B、C都在圆上
B.可以画一个圆,使A、B在圆上,C在圆外
C.可以画一个圆,使A、C在圆上,B在圆外
D.可以画一个圆,使B、C在圆上,A在圆内
7.已知⊙O的半径为3cm,圆心O到直线a的距离为2cm,则直线a与⊙O的位置关系为( )
A.相离 B.外切 C.相交 D.内切
8.观察下面4个选项中的图形及相应推理.其中正确的是( )
二、填空题(每小题3分,共24分)
9.若两圆外切,圆心距为8cm,一个圆的半径为3cm,则另一个圆的半径为 cm.
10.如图4,A、B、C是⊙O上的点,AB=2cm,∠ACB=30°,那么⊙O的半径为 .
11.为改善市区人民生活环境,市建设污水管网工程中,某圆柱型水管的直径为100cm,截面如图5,若管内污水的面宽AB=60cm,则污水的最大深度为 cm.
12.如图6是一个俱乐部的徽章.徽章的图案是一个金色的圆圈,中间是一个矩形,矩形中间又有一个蓝色的菱形,徽章的直径为2cm,则徽章内的菱形的边长为 cm.
13.两个同心圆的半径分别为3cm和4cm,大圆的弦BC与小圆相切,则BC= cm.
14.如图7,在⊙O中,弦AB=AC=5cm,BC=8cm,则⊙O的半径等于 cm.
15.等边三角形的边长为6,以三角形的外接圆的圆心为圆心,为半径作圆,则此圆与等边三角形三边的位置关系 .
16.两圆相切,圆心距为9cm,已知其中一圆半径为5cm,另一圆半径为 .
三、解答题(本大题共52分)
17.(本题8分)如图8是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数.
18.(本题8分)如图9,一条公路的转弯处是一段圆弧,点O是的圆心,E为上一点,OE⊥CD,垂足为F.已知CD=600m,EF=100m,求这段弯路的半径.
19.(本题10分)2005年秋季,希望中学举行了一次球类比赛,在足球比赛场上,李强、张胜两名同学互相配合向对方球门MN进攻,当李强同学冲到A点时,张胜同学已跟随冲到B点,如图10,请你从数学知识的角度考虑,此时李强同学是自己直接射门好,还是将球传给张胜同学,让张胜同学射门好,简述理由.
20.(本题12分)如图11,AB为⊙O的直径,C是⊙O上的一点,D在AB的延长线上,且∠DCB=∠A,
(1)CD与⊙O相切吗 如果相切,请你加以证明;如果不相切,请说明理由.
(2)若∠D=30°,BD=10cm.求⊙O的半径.
21.(本题14分)在同一平面内,已知点O到直线l的距离为5,以点O为圆心,r为半径画圆.探究、归纳:
(1)当r= 时,⊙O上有且只有一个点到直线l的距离等于3.
(2)当r= 时,⊙O上有且只有三个点到直线l的距离等于3.
(3)随着r的变化,⊙O上到直线l的距离等于3的点的个数有哪些变化?并求出相对应的r的值或取值范围(不必写出计算过程).
附加题(本题20分,不计入总分)
22.拓广探究:如图12,AB是⊙O的直径,C为圆周上一点,BD是⊙O的切线,B为切点.
(1)在图12(1)中,∠BAC=30°,求∠DBC的度数;
(2)在图12(2)中,∠BA1C=40°,求∠DBC的度数.
(3)在图12(3)中,∠BA1C=α,求∠DBC大小.
(4)通过(1)、(2)、(3)的探究,你发现了什么?用自己的语言叙述你的发现.
参考答案:
一、1~5.DBCCC 6~8.BCB
二、9.5 10.2cm 11.10 12.1 13.
14. 15.相切 16.4cm或14cm
三、17..
18.这段弯路的半径为500米.
19.李强把球转给张胜同学射门较好.理由略.
20.(1)相切,证明略.
(2)10cm.
21.(1)2;(2)8;
(3)当时,上没有点到直线的距离等于3.
当时,上有且只有1个点到直线的距离等于3.
当时,上有且只有2个点到直线的距离等于3.
当时,上有且只有3个点到直线的距离等于3.
当时,上有且只有4个点到直线的距离等于3.
附加题:
22.(1).
(2)连接,根据(1)可得.
(3)连接,根据(1)可得.
(4)在图(1)中,,在图(2),图(3),中,由此可得:圆的切线与弦所成的角等于它所夹的弧所对的圆周角.
同课章节目录
