第二十九章投影与视图复习教案(人教新课标九年级下)
文档属性
| 名称 | 第二十九章投影与视图复习教案(人教新课标九年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 131.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-04 00:00:00 | ||
图片预览

文档简介
第二十九章 投影与视图复习教案
(一)学习导引
1.情境引入
(1)日晷(guǐ)是我国古代利用日影测定时刻的仪器,它由“晷面”和“晷针”组成.当太阳光照在日晷上时,晷针的影子就回投向晷面.随着时间的推移,晷针的影子在晷面上慢慢的移动,以此来显示时刻.
(2)取若干长短不等的小棒及三角形、矩形纸片,观察它们在太阳光下的影子.
①固定投影面(即影子所在的平面),改变小棒或纸片的摆放位置和方向,它们的影子分别发生了什么变化?
②固定小棒或纸片,改变投影面的摆放位置和方向,它们的影子分别发生了什么变化?
2.知识提要
(1)投影的有关概念(物体的投影、投影线、投影面、中心投影、平行投影、正投影);
(2)投影的性质及其运用;
(3)三视图(主视图、左视图、俯视图)的意义.
(4)根据实物画三视图,根据三视图描述物体的形状.
3.案例分析
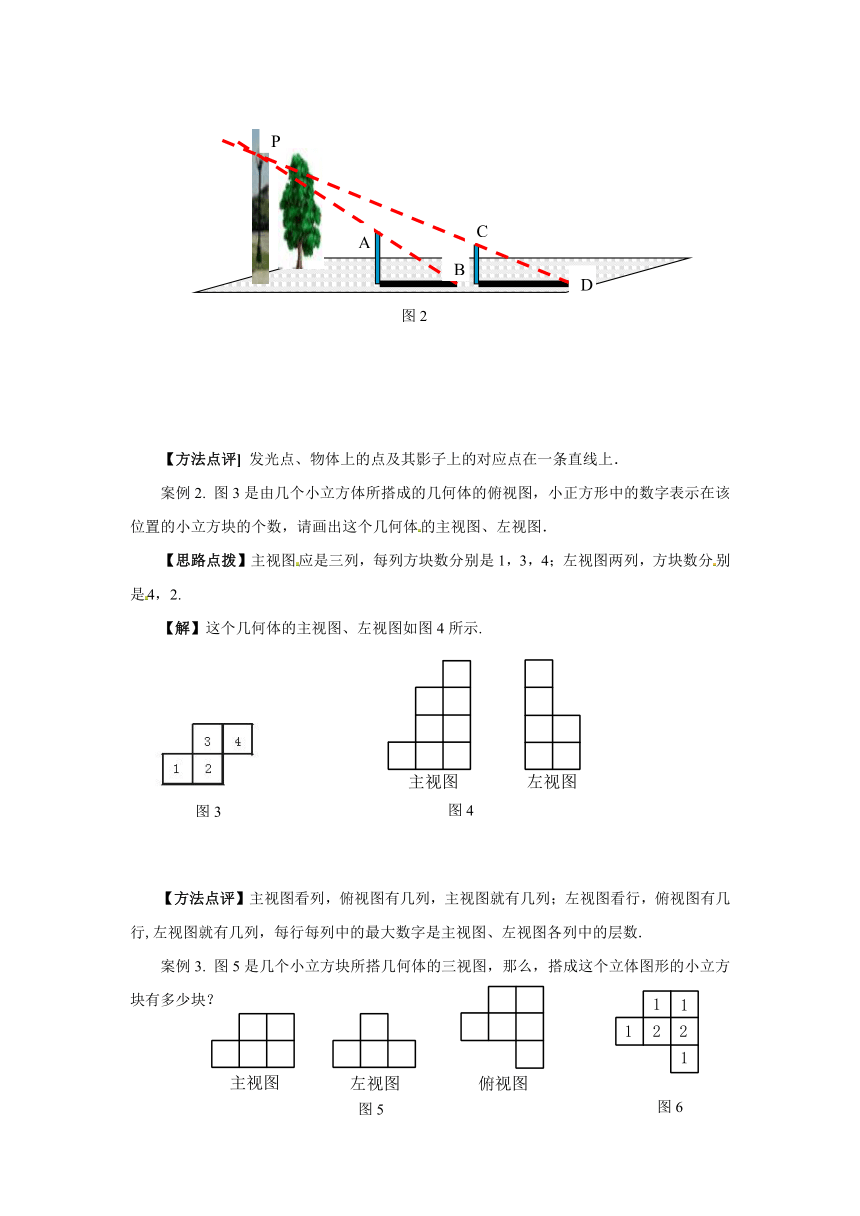
案例1. 如图1,请确定路灯灯泡的位置.
【思路点拨】经过一根木杆的顶端及其影子的顶端的线段是由路灯发出的光线的一部分,因此,只要找到这样的两条线段,它们所在的直线的交点就是灯泡的位置.
【解】如图2,直线AB与直线CD的交点P就是灯泡的位置.
【方法点评] 发光点、物体上的点及其影子上的对应点在一条直线上.
案例2. 图3是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的主视图、左视图.
【思路点拨】主视图应是三列,每列方块数分别是1,3,4;左视图两列,方块数分别是4,2.
【解】这个几何体的主视图、左视图如图4所示.
【方法点评】主视图看列,俯视图有几列,主视图就有几列;左视图看行,俯视图有几行,左视图就有几列,每行每列中的最大数字是主视图、左视图各列中的层数.
案例3. 图5是几个小立方块所搭几何体的三视图,那么,搭成这个立体图形的小立方块有多少块?
【思路点拨】先确定这个立体图形的大致形状,因此,我们以俯视图为基础,结合主视图和左视图,得到小立方块的个数.
【解】由左视图第一列和第三列只有一个小正方形,知俯视图的第一行和第三行的小正方形上的数字必为1,(俯视图中小正方形上的数字表示该位置小立方块的个数(如图6),由主视图第一列只有一个正方形,知俯视图的第一列的小正方形上的数字必为1,由主视图的第2、3列上有2个小正方形,知俯视图的第2列和第3列中至少有一个小正方形上的数字为2,从而只有它的第2行和第3行上的对应位置的小正方形上的数字都为2.所以这个立体图形由:1+1+1+2+2+1=8(个)小立方块搭成.
【方法点拨】解答此类问题的依据是:主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.
案例4.如图7(1),中间是一盏路灯,周围有一圈栏杆,图7(2)是其两幅俯视图(图中只画出了部分情形),其中一幅是白天阳光下的俯视图,另一幅是这盏路灯下的俯视图.你认为哪个是其白天的俯视图 哪个是其晚上的俯视图
【思路点拨】观察两个俯视图,发现左图中的栏杆的影子在栏杆所形成区域外,说明其影子是在灯光照射下形成的,因此左图是夜晚路灯下的俯视图,右图是白天阳光下的俯视图.
【解】左图是夜晚路灯下的俯视图,右图是白天阳光下的俯视图.
【方法点拨】连接实物的顶点与和其对应的影子的顶点的线段所在的直线应经过点光源.本题中栏杆在路灯下的影子不可能投在栏杆所围成的圆形区域内
(二)实践探究
探究1. 画出图8中由一些长方体搭成的几何体的三视图.
探究2. 图9是我国北方某地一棵树在一天不同时刻拍下的五张图片,仔细观察后回答下列问题.
(1)说出这五张图片所对应时间的先后顺序.
(2)根据生活经验,谈谈由早到晚该地物体影子的长短变化规律.
探究3. 与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子(如图10所示),树影是路灯灯光形成的.你能确定此时路灯光源的位置吗?
探究4. 根据物体的三视图(如图11所示),求它表示的几何体的表面积和体积.
图1
P
A
C
D
B
图2
图3
图4
图5
图6
图7(2)
图7(1)
图8
图9
图10
图11
(一)学习导引
1.情境引入
(1)日晷(guǐ)是我国古代利用日影测定时刻的仪器,它由“晷面”和“晷针”组成.当太阳光照在日晷上时,晷针的影子就回投向晷面.随着时间的推移,晷针的影子在晷面上慢慢的移动,以此来显示时刻.
(2)取若干长短不等的小棒及三角形、矩形纸片,观察它们在太阳光下的影子.
①固定投影面(即影子所在的平面),改变小棒或纸片的摆放位置和方向,它们的影子分别发生了什么变化?
②固定小棒或纸片,改变投影面的摆放位置和方向,它们的影子分别发生了什么变化?
2.知识提要
(1)投影的有关概念(物体的投影、投影线、投影面、中心投影、平行投影、正投影);
(2)投影的性质及其运用;
(3)三视图(主视图、左视图、俯视图)的意义.
(4)根据实物画三视图,根据三视图描述物体的形状.
3.案例分析
案例1. 如图1,请确定路灯灯泡的位置.
【思路点拨】经过一根木杆的顶端及其影子的顶端的线段是由路灯发出的光线的一部分,因此,只要找到这样的两条线段,它们所在的直线的交点就是灯泡的位置.
【解】如图2,直线AB与直线CD的交点P就是灯泡的位置.
【方法点评] 发光点、物体上的点及其影子上的对应点在一条直线上.
案例2. 图3是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,请画出这个几何体的主视图、左视图.
【思路点拨】主视图应是三列,每列方块数分别是1,3,4;左视图两列,方块数分别是4,2.
【解】这个几何体的主视图、左视图如图4所示.
【方法点评】主视图看列,俯视图有几列,主视图就有几列;左视图看行,俯视图有几行,左视图就有几列,每行每列中的最大数字是主视图、左视图各列中的层数.
案例3. 图5是几个小立方块所搭几何体的三视图,那么,搭成这个立体图形的小立方块有多少块?
【思路点拨】先确定这个立体图形的大致形状,因此,我们以俯视图为基础,结合主视图和左视图,得到小立方块的个数.
【解】由左视图第一列和第三列只有一个小正方形,知俯视图的第一行和第三行的小正方形上的数字必为1,(俯视图中小正方形上的数字表示该位置小立方块的个数(如图6),由主视图第一列只有一个正方形,知俯视图的第一列的小正方形上的数字必为1,由主视图的第2、3列上有2个小正方形,知俯视图的第2列和第3列中至少有一个小正方形上的数字为2,从而只有它的第2行和第3行上的对应位置的小正方形上的数字都为2.所以这个立体图形由:1+1+1+2+2+1=8(个)小立方块搭成.
【方法点拨】解答此类问题的依据是:主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.
案例4.如图7(1),中间是一盏路灯,周围有一圈栏杆,图7(2)是其两幅俯视图(图中只画出了部分情形),其中一幅是白天阳光下的俯视图,另一幅是这盏路灯下的俯视图.你认为哪个是其白天的俯视图 哪个是其晚上的俯视图
【思路点拨】观察两个俯视图,发现左图中的栏杆的影子在栏杆所形成区域外,说明其影子是在灯光照射下形成的,因此左图是夜晚路灯下的俯视图,右图是白天阳光下的俯视图.
【解】左图是夜晚路灯下的俯视图,右图是白天阳光下的俯视图.
【方法点拨】连接实物的顶点与和其对应的影子的顶点的线段所在的直线应经过点光源.本题中栏杆在路灯下的影子不可能投在栏杆所围成的圆形区域内
(二)实践探究
探究1. 画出图8中由一些长方体搭成的几何体的三视图.
探究2. 图9是我国北方某地一棵树在一天不同时刻拍下的五张图片,仔细观察后回答下列问题.
(1)说出这五张图片所对应时间的先后顺序.
(2)根据生活经验,谈谈由早到晚该地物体影子的长短变化规律.
探究3. 与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树.晚上,幕墙反射路灯灯光形成了那盆花的影子(如图10所示),树影是路灯灯光形成的.你能确定此时路灯光源的位置吗?
探究4. 根据物体的三视图(如图11所示),求它表示的几何体的表面积和体积.
图1
P
A
C
D
B
图2
图3
图4
图5
图6
图7(2)
图7(1)
图8
图9
图10
图11
