28.1锐角三角函数(3)(17张)
文档属性
| 名称 | 28.1锐角三角函数(3)(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 671.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-04 20:34:07 | ||
图片预览





文档简介
(共17张PPT)
28.1 锐角三角函数(3)
复习:
1.锐角三角函数的定义
在 中,
∠A的余弦 :
∠A的正弦:
思
考
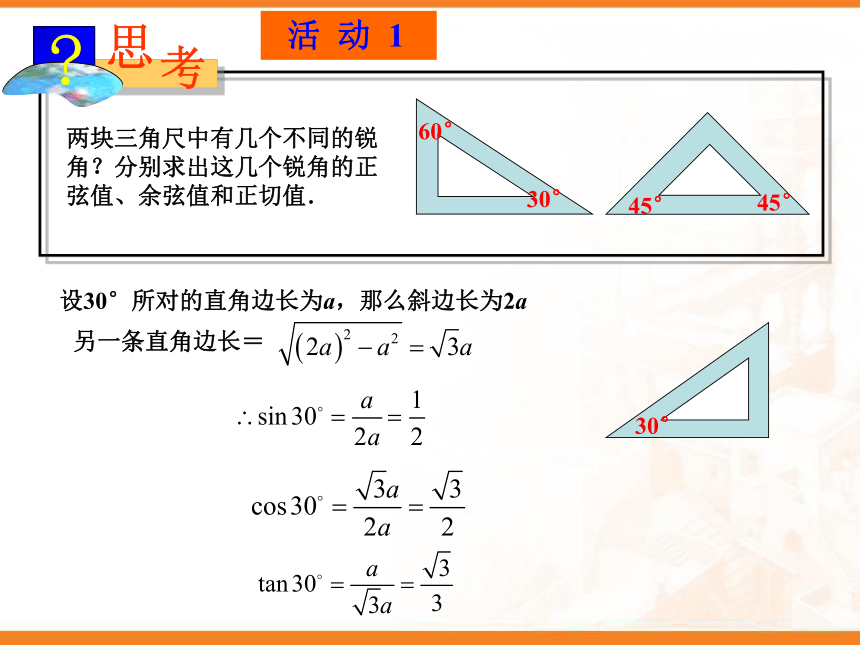
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
活 动 1
设两条直角边长为a,则斜边长=
60°
45°
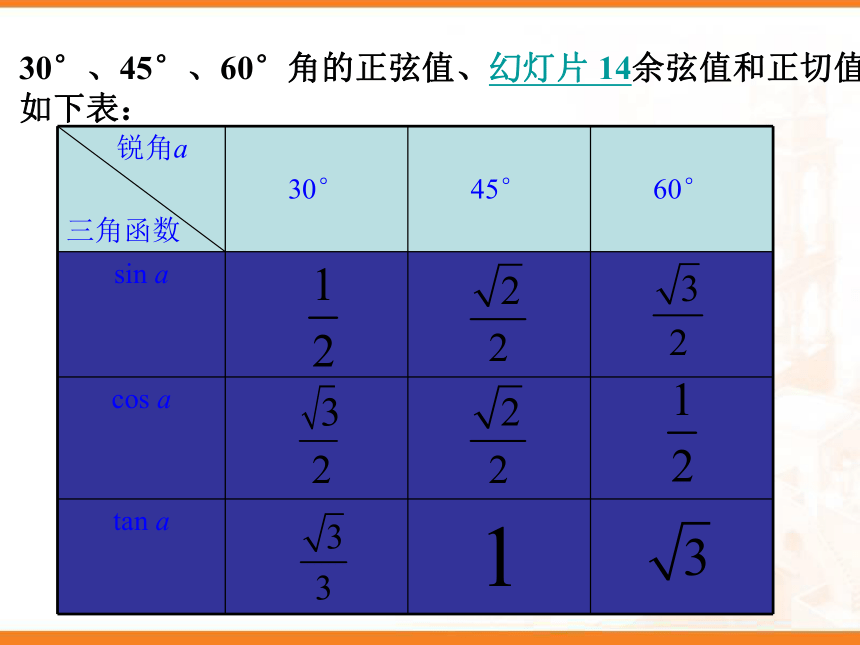
30°、45°、60°角的正弦值、幻灯片 14余弦值和正切值如下表:
锐角a 三角函数 30° 45° 60°
sin a
cos a
tan a
例1.计算:
利用特殊的三角函数值进行计算:
(1)2sin30°- 3cos60 °
(2)cos 45°+tan60°·cos60°
(3) cos30°- sin45°+tan45°· cos60°
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
例2 求下列各式的值:
(1)cos260°+sin260°
(2)
解: (1) cos260°+sin260°
=1
(2)
=0
解简单的三角方程
例3.求适合下列各式的锐角α
例4 (1)如图,在Rt△ABC中,∠C=90°,
,
求∠A的度数.
解: (1)在图中,
A
B
C
(2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍,求 a .
解: (2)在图中,
A
B
O
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
练习
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
三角函数的单调性 :
观察特殊角的三角函数表,发现规律:
(1)当 时, α的正弦值随着:
角度的增大而增大,随着角度的减小而减小;
(2)当 时, α的余弦值随着:
角度的增大而减小,随着角度的减小而增大;
(3)当 时, α的正切值随着:
角度的增大而增大,随着角度的减小而减小.
课外思考:
利用上述规律可以比较同名三角函数值的大小
例5 填空:比较大小
°
68
sin
3
)
(
﹥
﹥
﹤
例6 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
将实际问题数学化.
A
C
O
B
D
┌
●
2.5
小结 :
我们学习了30°, 45°, 60°这几类特殊角的三角函数值.
28.1 锐角三角函数(3)
复习:
1.锐角三角函数的定义
在 中,
∠A的余弦 :
∠A的正弦:
思
考
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
活 动 1
设两条直角边长为a,则斜边长=
60°
45°
30°、45°、60°角的正弦值、幻灯片 14余弦值和正切值如下表:
锐角a 三角函数 30° 45° 60°
sin a
cos a
tan a
例1.计算:
利用特殊的三角函数值进行计算:
(1)2sin30°- 3cos60 °
(2)cos 45°+tan60°·cos60°
(3) cos30°- sin45°+tan45°· cos60°
老师提示:
Sin2600表示(sin600)2,
cos2600表示(cos600)2,其余类推.
例2 求下列各式的值:
(1)cos260°+sin260°
(2)
解: (1) cos260°+sin260°
=1
(2)
=0
解简单的三角方程
例3.求适合下列各式的锐角α
例4 (1)如图,在Rt△ABC中,∠C=90°,
,
求∠A的度数.
解: (1)在图中,
A
B
C
(2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍,求 a .
解: (2)在图中,
A
B
O
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
练习
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
三角函数的单调性 :
观察特殊角的三角函数表,发现规律:
(1)当 时, α的正弦值随着:
角度的增大而增大,随着角度的减小而减小;
(2)当 时, α的余弦值随着:
角度的增大而减小,随着角度的减小而增大;
(3)当 时, α的正切值随着:
角度的增大而增大,随着角度的减小而减小.
课外思考:
利用上述规律可以比较同名三角函数值的大小
例5 填空:比较大小
°
68
sin
3
)
(
﹥
﹥
﹤
例6 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
将实际问题数学化.
A
C
O
B
D
┌
●
2.5
小结 :
我们学习了30°, 45°, 60°这几类特殊角的三角函数值.
