2020-2021学年湘教新版八年级下册数学期中复习试卷1(Word版含解析)
文档属性
| 名称 | 2020-2021学年湘教新版八年级下册数学期中复习试卷1(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-27 09:11:11 | ||
图片预览



文档简介
2020-2021学年湘教新版八年级下册数学期中复习试卷1
一.选择题(共10小题,满分30分,每小题3分)
1.如图,一架云梯长25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的底部在水平方向上向右滑动了8米,那么梯子的底端下滑( )米.
A.10米
B.8米
C.6米
D.4米
2.到三角形的三边距离相等的点是( )
A.三角形三条高的交点
B.三角形三条内角平分线的交点
C.三角形三条中线的交点
D.三角形三条边的垂直平分线的交点
3.若菱形的两条对角线长分别是6和8,则它的周长为( )
A.20
B.24
C.40
D.48
4.平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为( )
A.4cm,4cm,8cm,8cm
B.5cm,5cm,7cm,7cm
C.5.5cm,5.5cm,6.5cm,6.5cm
D.3cm,3cm,9cm,9cm
5.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )
A.15°
B.20°
C.25°
D.30°
6.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
A.85°
B.80°
C.75°
D.70°
7.如图,在平行四边形ABCD中AB=6,BC=8,BD的垂直平分线交AD于点E,则△ABE的周长是( )
A.7
B.10
C.13
D.14
8.如图所示,在?ABCD中,对角线AC、BD相交于点O,且AB≠AD,则下列式子不正确的是( )
A.AC⊥BD
B.AB=CD
C.BO=OD
D.∠BAD=∠BCD
9.如图,已知菱形ABCD,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.16
B.12
C.24
D.18
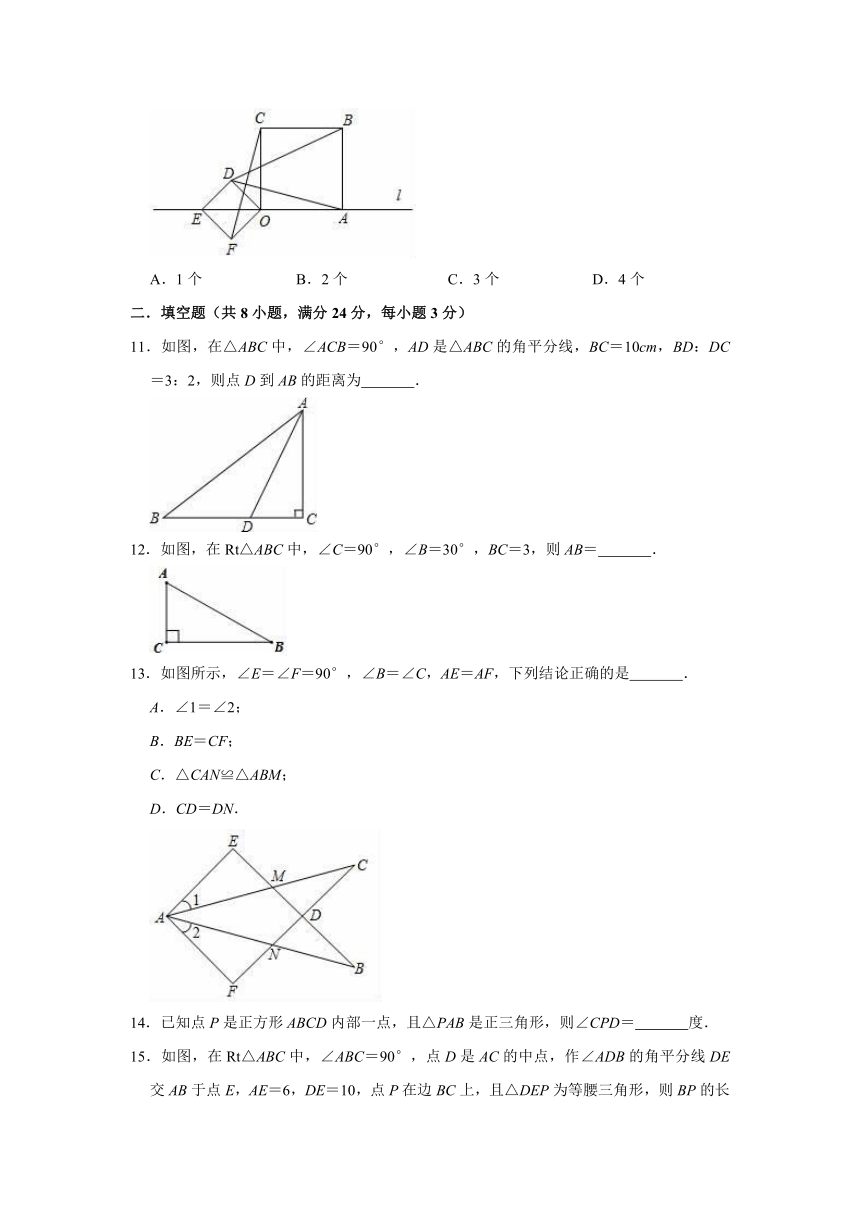
10.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=,AB=3,给出下列结论:①∠COD=45°,②AE=5,③CF=BD=,④△COF的面积S△COF=3,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,满分24分,每小题3分)
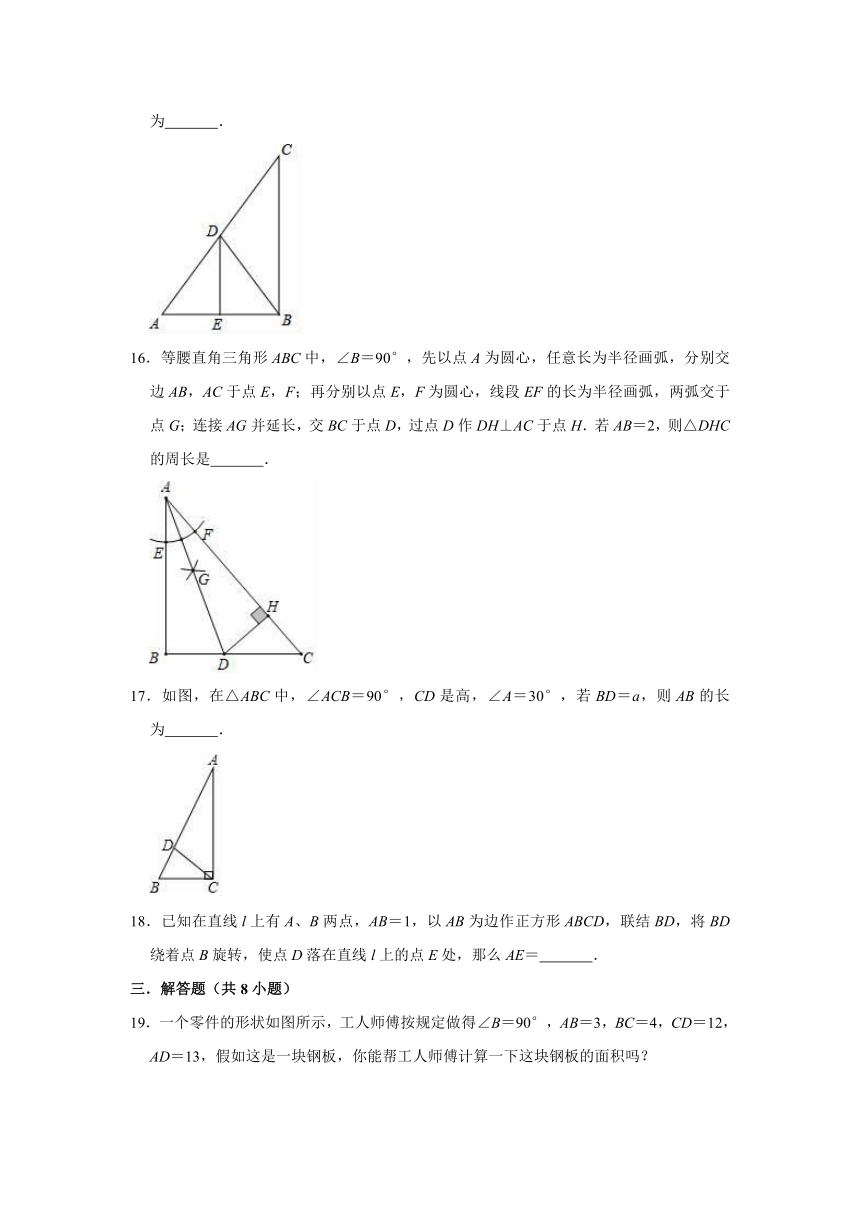
11.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为
.
12.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=3,则AB=
.
13.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论正确的是
.
A.∠1=∠2;
B.BE=CF;
C.△CAN≌△ABM;
D.CD=DN.
14.已知点P是正方形ABCD内部一点,且△PAB是正三角形,则∠CPD=
度.
15.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,AE=6,DE=10,点P在边BC上,且△DEP为等腰三角形,则BP的长为
.
16.等腰直角三角形ABC中,∠B=90°,先以点A为圆心,任意长为半径画弧,分别交边AB,AC于点E,F;再分别以点E,F为圆心,线段EF的长为半径画弧,两弧交于点G;连接AG并延长,交BC于点D,过点D作DH⊥AC于点H.若AB=2,则△DHC的周长是
.
17.如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,若BD=a,则AB的长为
.
18.已知在直线l上有A、B两点,AB=1,以AB为边作正方形ABCD,联结BD,将BD绕着点B旋转,使点D落在直线l上的点E处,那么AE=
.
三.解答题(共8小题)
19.一个零件的形状如图所示,工人师傅按规定做得∠B=90°,AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
20.如图,在?ABCD中,对角线AC与BD相交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:AE=CF;
(2)若AC平分∠HAG,判断四边形AGCH的形状,并证明你的结论.
21.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
22.如图,在菱形ABCD中,E,F分别是AB和CD的中点,连接AF,CE.
(1)求证:AF=CE;
(2)试确定,当菱形ABCD再满足一个什么条件时,四边形AECF为矩形?请说明理由.
23.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD、EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
24.如图,平行四边形ABCD中,过对角线BD上一点P做EF∥BC,GH∥AB,
(1)写出图中所有的平行四边形(包括平行四边形ABCD)的个数;
(2)写出图中所有面积相等的平行四边形.
25.如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
(1)求证:CF=AD;
(2)若∠ACB=90°,试判断四边形BFCD的形状,并说明理由.
26.如图,已知菱形ABCD的边长为2,∠DAB=60°,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.连接BD.
(1)图中有几对三角形全等?试选取一对全等的三角形给予证明;
(2)判断△BEF的形状,并说明理由.
(3)当△BEF的面积取得最小值时,试判断此时EF与BD的位置关系.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:如图标上字母.
在Rt△AOB中,∠AOB=90°,AB=25,OB=7,
∴OA==24.
在Rt△COD中,∠COD=90°,CD=25,OD=7+8=15,
∴OC==20,
∴AC=OA﹣OC=4.
故选:D.
2.解:到三角形的三边距离相等的点是:三角形三条内角平分线的交点.
故选:B.
3.解:如图所示,
根据题意得AO=×8=4,BO=×6=3,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BD,
∴△AOB是直角三角形,
∴AB====5,
∴此菱形的周长为:5×4=20.
故选:A.
4.解:可设两边分别为xcm,ycm,
由题意可得,
解得,
所以平行四边形的各边长为5cm,5cm,7cm,7cm,
故选:B.
5.解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF=BC,PE=AD,
∵AD=BC,
∴PF=PE,
故△EPF是等腰三角形.
∵∠PEF=30°,
∴∠PEF=∠PFE=30°.
故选:D.
6.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠EAO=15°,
∴∠BAO=45°+15°=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,OB=AB,
∴∠OBE=90﹣60°=30°,OB=BE,
∴∠BOE=(180°﹣30°)=75°.
故选:C.
7.解:∵BD的垂直平分线交AD于点E,
∴BE=ED,
∵四边形ABCD是平行四边形,
∴DC=AB=6,AD=BC=8,
∴△ABE的周长为:AB+AE+ED=AD+AB=6+8=14,
故选:D.
8.解:∵四边形ABCD为平行四边形,
∴AB=CD,则选项B正确;
又根据平行四边形的对角线互相平分,
∴BO=OD,则选项C正确;
又∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠ABC+∠BCD=180°,∠BAD+∠ABC=180°,
∴∠BAD=∠BCD,则选项D正确;
由BO=OD,假设AC⊥BD,
又∵OA=OA,
∴△ABO≌△ADO,
∴AB=AD与已知AB≠AD矛盾,
∴AC不垂直BD,则选项A错误.
故选:A.
9.解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=BC=4,
∴以AC为边长的正方形ACEF的周长为:4AC=16.
故选:A.
10.解:①∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,
故正确;
②∵EF=,
∴OE=2,
∵AO=AB=3,
∴AE=AO+OE=2+3=5,
故正确;
③作DH⊥AB于H,作FG⊥CO交CO的延长线于G,
则FG=1,
CF=,
BH=3﹣1=2,
DH=3+1=4,
BD=,
故错误;
④△COF的面积S△COF=×3×1=,
故错误;
故选:B.
二.填空题(共8小题,满分24分,每小题3分)
11.解:∵BC=10cm,BD:DC=3:2,
∴DC=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
故答案为4cm.
12.解:∵Rt△ABC中,∠C=90°,∠B=30°.
∴AB=2AC.
设AC=x.则AB=2x.
∴x2+32=(2x)2
∴x=.
∴.
故答案为:2.
13.解:如图,
∵∠E=∠F=90°,∠B=∠C,AE=AF,
∴Rt△ABE≌Rt△ACF(AAS),
∴∠FAC=∠EAB,BE=CF,AB=AC,
∴∠1=∠2,
故A,B正确;
又∠B=∠C,∠CAN=∠BAM,
∴△ACN≌△ABM(ASA),
故C错误;
∵△ACN≌△ABM(ASA),
∴AN=AM,
∴MC=BN,
而∠B=∠C,∠CDM=∠BDN,
∴△DMC≌△DMB(AAS),
∴DC=DB,
∴DC≠DN,
故D错误.
故答案为:A,B;
14.解:如图,
∵四边形ABCD是正方形,
∴AD=AB=BC,∠DAB=∠ABC=90°,
∵△ABP是等边三角形,
∴AP=BP=AB,∠PAB=∠PBA=60°,
∴AP=AD=BP=BC,∠DAP=∠CBP=30°.
∴∠BCP=∠BPC=∠APD=∠ADP=75°,
∴∠PDC=∠PCD=15°,
∴∠CPD=180°﹣∠PDC﹣∠PCD=180°﹣15°﹣15°=150°.
故答案为:150.
15.解:
如图:在Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴DB=AD=DC,
∵DE是∠ADB的角平分线,
∴AE=BE=6,DE=10,
①DE中点G作GP⊥BC于点P,
得矩形EGPB,所以PB=DE=5;
②作DP=DE,交BC于两个点P′和P,作EP④=ED交BC于点P④,
作DF⊥BC于点F,得矩形EBFD,
∴DF=BE=6,BF=DE=10,
∴根据勾股定理,得P′F=BP4=8,
∴P′B=10﹣8=2,或P″B=10+8=18.
所以BP有四个值,分别为2、5、8、18.
故答案为2、5、8、18.
16.解:由题意可得AD是∠BAC的平分线,
∴AB=AH,BD=DH,
∵AB=2,△ABC是等腰直角三角形,
∴AH=2,AC=2,∠C=45°,
∴CH=2﹣2,
∴△DHC的周长=DH+DC+CH=BD+DC+CH=BC+CH=2+2﹣2=2,
故答案为:2.
17.解:∵CD是高,∠A=30°,
∴∠BCD=30°,
∴BC=2BD=2a,
∵∠ACB=90°,∠A=30°,
∴AB=2BC=4a,
故答案为:4a.
18.解:如图1,当点E在AB的延长线上,
∵正方形ABCD中,AB=AD=1,∠DAB=90°,
∴BD==,
∵将BD绕着点B旋转,使点D落在直线l上的点E处,
∴BD=BE=,
∴AE=AB+BE=1+;
如图2,当点E在BA的延长线上,
同理可得BD=BE=,
∴AE=BE﹣AB=﹣1.
∴AE的长为+1或﹣1.
故答案为:
+1或﹣1.
三.解答题(共8小题)
19.解:∵42+32=52,52+122=132,
即AB2+BC2=AC2,故∠B=90°,
同理,∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD
=×3×4+×5×12
=6+30
=36.
答:这块钢板的面积等于36.
20.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)四边形AGCH是菱形.理由如下:
∵△AOE≌△COF,
∴∠EAO=∠FCO,
∴AG∥CH,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AGCH是平行四边形,
∵AD∥BC,
∴∠HAC=∠ACB,
∵AC平分∠HAG,
∴∠HAC=∠GAC,
∵∠GAC=∠ACB,
∴GA=GC,
∴平行四边形AGCH是菱形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
22.(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD.
∵E、F分别是AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF.
又∵AE∥CF,
∴四边形AECF是平行四边形.
∴AF=CE;
(2)菱形ABCD的内角∠B=60°时,则四边形AECF为矩形,
理由如下:
连接AC,
∵AB=BC,
∴△ABC是等边三角形,
∵AE=BE,
∴CE⊥AB,
∴∠AEC=90°,
∴四边形AECF为矩形.
23.证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴?ADCE是矩形.
24.解:(1)图中所有的平行四边形(包括?ABCD)有四边形AEPG、ABHG、BEPH、HCFP、BEFC、HCDG、PGDF、AEDF、ABCD,共9个.
(2)?AEPG和?PHCF面积相等;
?ABHG和?EBCF面积相等;
?AEFD和?GHCD面积相等.
25.(1)证明∵AE是DC边上的中线,
∴AE=FE,
∵CF∥AB,
∴∠ADE=∠FCE,∠DAE=∠CFE.
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=DA.
(2)∵CD是△ABC的中线,
∴D是AB的中点,
∴AD=BD,
∵△ADE≌△FCE,
∴AD=CF,
∴BD=CF,
∵AB∥CF,
∴BD∥CF,
∴四边形BFCD是平行四边形,
∵∠ACB=90°,
∴△ACB是直角三角形,
∴CD=AB,
∵BD=AB,
∴BD=CD,
∴四边形BFCD是菱形.
26.解:(1)△BAE≌△BDF,△BDE≌△BCF,△BAD≌△BCD,共三对;
证明:△BDE≌△BCF.
在△BDE和△BCF中,
,
故△BDE≌△BCF.
(2)△BEF为正三角形.
理由:∵△BDE≌△BCF,
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为正三角形;
(3)设BE=BF=EF=x,
则S△BEF=?x?x?sin60°=x2,
当BE⊥AD时,x最小=2×sin60°=,此时△BEF的面积最小,
此时点E、F分别位于AD、CD的中点,
故此时BD垂直平分EF.
一.选择题(共10小题,满分30分,每小题3分)
1.如图,一架云梯长25米,斜靠在一面墙上,梯子底端离墙7米,如果梯子的底部在水平方向上向右滑动了8米,那么梯子的底端下滑( )米.
A.10米
B.8米
C.6米
D.4米
2.到三角形的三边距离相等的点是( )
A.三角形三条高的交点
B.三角形三条内角平分线的交点
C.三角形三条中线的交点
D.三角形三条边的垂直平分线的交点
3.若菱形的两条对角线长分别是6和8,则它的周长为( )
A.20
B.24
C.40
D.48
4.平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为( )
A.4cm,4cm,8cm,8cm
B.5cm,5cm,7cm,7cm
C.5.5cm,5.5cm,6.5cm,6.5cm
D.3cm,3cm,9cm,9cm
5.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠PFE的度数是( )
A.15°
B.20°
C.25°
D.30°
6.如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
A.85°
B.80°
C.75°
D.70°
7.如图,在平行四边形ABCD中AB=6,BC=8,BD的垂直平分线交AD于点E,则△ABE的周长是( )
A.7
B.10
C.13
D.14
8.如图所示,在?ABCD中,对角线AC、BD相交于点O,且AB≠AD,则下列式子不正确的是( )
A.AC⊥BD
B.AB=CD
C.BO=OD
D.∠BAD=∠BCD
9.如图,已知菱形ABCD,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.16
B.12
C.24
D.18
10.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=,AB=3,给出下列结论:①∠COD=45°,②AE=5,③CF=BD=,④△COF的面积S△COF=3,其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,满分24分,每小题3分)
11.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为
.
12.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=3,则AB=
.
13.如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论正确的是
.
A.∠1=∠2;
B.BE=CF;
C.△CAN≌△ABM;
D.CD=DN.
14.已知点P是正方形ABCD内部一点,且△PAB是正三角形,则∠CPD=
度.
15.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,AE=6,DE=10,点P在边BC上,且△DEP为等腰三角形,则BP的长为
.
16.等腰直角三角形ABC中,∠B=90°,先以点A为圆心,任意长为半径画弧,分别交边AB,AC于点E,F;再分别以点E,F为圆心,线段EF的长为半径画弧,两弧交于点G;连接AG并延长,交BC于点D,过点D作DH⊥AC于点H.若AB=2,则△DHC的周长是
.
17.如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,若BD=a,则AB的长为
.
18.已知在直线l上有A、B两点,AB=1,以AB为边作正方形ABCD,联结BD,将BD绕着点B旋转,使点D落在直线l上的点E处,那么AE=
.
三.解答题(共8小题)
19.一个零件的形状如图所示,工人师傅按规定做得∠B=90°,AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
20.如图,在?ABCD中,对角线AC与BD相交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:AE=CF;
(2)若AC平分∠HAG,判断四边形AGCH的形状,并证明你的结论.
21.如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.
22.如图,在菱形ABCD中,E,F分别是AB和CD的中点,连接AF,CE.
(1)求证:AF=CE;
(2)试确定,当菱形ABCD再满足一个什么条件时,四边形AECF为矩形?请说明理由.
23.如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD、EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
24.如图,平行四边形ABCD中,过对角线BD上一点P做EF∥BC,GH∥AB,
(1)写出图中所有的平行四边形(包括平行四边形ABCD)的个数;
(2)写出图中所有面积相等的平行四边形.
25.如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
(1)求证:CF=AD;
(2)若∠ACB=90°,试判断四边形BFCD的形状,并说明理由.
26.如图,已知菱形ABCD的边长为2,∠DAB=60°,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.连接BD.
(1)图中有几对三角形全等?试选取一对全等的三角形给予证明;
(2)判断△BEF的形状,并说明理由.
(3)当△BEF的面积取得最小值时,试判断此时EF与BD的位置关系.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:如图标上字母.
在Rt△AOB中,∠AOB=90°,AB=25,OB=7,
∴OA==24.
在Rt△COD中,∠COD=90°,CD=25,OD=7+8=15,
∴OC==20,
∴AC=OA﹣OC=4.
故选:D.
2.解:到三角形的三边距离相等的点是:三角形三条内角平分线的交点.
故选:B.
3.解:如图所示,
根据题意得AO=×8=4,BO=×6=3,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AC⊥BD,
∴△AOB是直角三角形,
∴AB====5,
∴此菱形的周长为:5×4=20.
故选:A.
4.解:可设两边分别为xcm,ycm,
由题意可得,
解得,
所以平行四边形的各边长为5cm,5cm,7cm,7cm,
故选:B.
5.解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,
∴FP,PE分别是△CDB与△DAB的中位线,
∴PF=BC,PE=AD,
∵AD=BC,
∴PF=PE,
故△EPF是等腰三角形.
∵∠PEF=30°,
∴∠PEF=∠PFE=30°.
故选:D.
6.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠EAO=15°,
∴∠BAO=45°+15°=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,OB=AB,
∴∠OBE=90﹣60°=30°,OB=BE,
∴∠BOE=(180°﹣30°)=75°.
故选:C.
7.解:∵BD的垂直平分线交AD于点E,
∴BE=ED,
∵四边形ABCD是平行四边形,
∴DC=AB=6,AD=BC=8,
∴△ABE的周长为:AB+AE+ED=AD+AB=6+8=14,
故选:D.
8.解:∵四边形ABCD为平行四边形,
∴AB=CD,则选项B正确;
又根据平行四边形的对角线互相平分,
∴BO=OD,则选项C正确;
又∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴∠ABC+∠BCD=180°,∠BAD+∠ABC=180°,
∴∠BAD=∠BCD,则选项D正确;
由BO=OD,假设AC⊥BD,
又∵OA=OA,
∴△ABO≌△ADO,
∴AB=AD与已知AB≠AD矛盾,
∴AC不垂直BD,则选项A错误.
故选:A.
9.解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=BC=4,
∴以AC为边长的正方形ACEF的周长为:4AC=16.
故选:A.
10.解:①∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,
故正确;
②∵EF=,
∴OE=2,
∵AO=AB=3,
∴AE=AO+OE=2+3=5,
故正确;
③作DH⊥AB于H,作FG⊥CO交CO的延长线于G,
则FG=1,
CF=,
BH=3﹣1=2,
DH=3+1=4,
BD=,
故错误;
④△COF的面积S△COF=×3×1=,
故错误;
故选:B.
二.填空题(共8小题,满分24分,每小题3分)
11.解:∵BC=10cm,BD:DC=3:2,
∴DC=4cm,
∵AD是△ABC的角平分线,∠ACB=90°,
∴点D到AB的距离等于DC,即点D到AB的距离等于4cm.
故答案为4cm.
12.解:∵Rt△ABC中,∠C=90°,∠B=30°.
∴AB=2AC.
设AC=x.则AB=2x.
∴x2+32=(2x)2
∴x=.
∴.
故答案为:2.
13.解:如图,
∵∠E=∠F=90°,∠B=∠C,AE=AF,
∴Rt△ABE≌Rt△ACF(AAS),
∴∠FAC=∠EAB,BE=CF,AB=AC,
∴∠1=∠2,
故A,B正确;
又∠B=∠C,∠CAN=∠BAM,
∴△ACN≌△ABM(ASA),
故C错误;
∵△ACN≌△ABM(ASA),
∴AN=AM,
∴MC=BN,
而∠B=∠C,∠CDM=∠BDN,
∴△DMC≌△DMB(AAS),
∴DC=DB,
∴DC≠DN,
故D错误.
故答案为:A,B;
14.解:如图,
∵四边形ABCD是正方形,
∴AD=AB=BC,∠DAB=∠ABC=90°,
∵△ABP是等边三角形,
∴AP=BP=AB,∠PAB=∠PBA=60°,
∴AP=AD=BP=BC,∠DAP=∠CBP=30°.
∴∠BCP=∠BPC=∠APD=∠ADP=75°,
∴∠PDC=∠PCD=15°,
∴∠CPD=180°﹣∠PDC﹣∠PCD=180°﹣15°﹣15°=150°.
故答案为:150.
15.解:
如图:在Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴DB=AD=DC,
∵DE是∠ADB的角平分线,
∴AE=BE=6,DE=10,
①DE中点G作GP⊥BC于点P,
得矩形EGPB,所以PB=DE=5;
②作DP=DE,交BC于两个点P′和P,作EP④=ED交BC于点P④,
作DF⊥BC于点F,得矩形EBFD,
∴DF=BE=6,BF=DE=10,
∴根据勾股定理,得P′F=BP4=8,
∴P′B=10﹣8=2,或P″B=10+8=18.
所以BP有四个值,分别为2、5、8、18.
故答案为2、5、8、18.
16.解:由题意可得AD是∠BAC的平分线,
∴AB=AH,BD=DH,
∵AB=2,△ABC是等腰直角三角形,
∴AH=2,AC=2,∠C=45°,
∴CH=2﹣2,
∴△DHC的周长=DH+DC+CH=BD+DC+CH=BC+CH=2+2﹣2=2,
故答案为:2.
17.解:∵CD是高,∠A=30°,
∴∠BCD=30°,
∴BC=2BD=2a,
∵∠ACB=90°,∠A=30°,
∴AB=2BC=4a,
故答案为:4a.
18.解:如图1,当点E在AB的延长线上,
∵正方形ABCD中,AB=AD=1,∠DAB=90°,
∴BD==,
∵将BD绕着点B旋转,使点D落在直线l上的点E处,
∴BD=BE=,
∴AE=AB+BE=1+;
如图2,当点E在BA的延长线上,
同理可得BD=BE=,
∴AE=BE﹣AB=﹣1.
∴AE的长为+1或﹣1.
故答案为:
+1或﹣1.
三.解答题(共8小题)
19.解:∵42+32=52,52+122=132,
即AB2+BC2=AC2,故∠B=90°,
同理,∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD
=×3×4+×5×12
=6+30
=36.
答:这块钢板的面积等于36.
20.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DF,
即OE=OF,
又∵∠AOE=∠COF,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)四边形AGCH是菱形.理由如下:
∵△AOE≌△COF,
∴∠EAO=∠FCO,
∴AG∥CH,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形AGCH是平行四边形,
∵AD∥BC,
∴∠HAC=∠ACB,
∵AC平分∠HAG,
∴∠HAC=∠GAC,
∵∠GAC=∠ACB,
∴GA=GC,
∴平行四边形AGCH是菱形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
∴BE=CD;
(2)∵BE=AB,BF平分∠ABE,
∴AF=EF,
在△ADF和△ECF中,
,
∴△ADF≌△ECF(ASA),
∴DF=CF,
又∵AF=EF,
∴四边形ACED是平行四边形.
22.(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD.
∵E、F分别是AB、CD的中点,
∴AE=AB,CF=CD,
∴AE=CF.
又∵AE∥CF,
∴四边形AECF是平行四边形.
∴AF=CE;
(2)菱形ABCD的内角∠B=60°时,则四边形AECF为矩形,
理由如下:
连接AC,
∵AB=BC,
∴△ABC是等边三角形,
∵AE=BE,
∴CE⊥AB,
∴∠AEC=90°,
∴四边形AECF为矩形.
23.证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴?ADCE是矩形.
24.解:(1)图中所有的平行四边形(包括?ABCD)有四边形AEPG、ABHG、BEPH、HCFP、BEFC、HCDG、PGDF、AEDF、ABCD,共9个.
(2)?AEPG和?PHCF面积相等;
?ABHG和?EBCF面积相等;
?AEFD和?GHCD面积相等.
25.(1)证明∵AE是DC边上的中线,
∴AE=FE,
∵CF∥AB,
∴∠ADE=∠FCE,∠DAE=∠CFE.
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=DA.
(2)∵CD是△ABC的中线,
∴D是AB的中点,
∴AD=BD,
∵△ADE≌△FCE,
∴AD=CF,
∴BD=CF,
∵AB∥CF,
∴BD∥CF,
∴四边形BFCD是平行四边形,
∵∠ACB=90°,
∴△ACB是直角三角形,
∴CD=AB,
∵BD=AB,
∴BD=CD,
∴四边形BFCD是菱形.
26.解:(1)△BAE≌△BDF,△BDE≌△BCF,△BAD≌△BCD,共三对;
证明:△BDE≌△BCF.
在△BDE和△BCF中,
,
故△BDE≌△BCF.
(2)△BEF为正三角形.
理由:∵△BDE≌△BCF,
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为正三角形;
(3)设BE=BF=EF=x,
则S△BEF=?x?x?sin60°=x2,
当BE⊥AD时,x最小=2×sin60°=,此时△BEF的面积最小,
此时点E、F分别位于AD、CD的中点,
故此时BD垂直平分EF.
同课章节目录
