2020-2021学年湘教新版九年级下册数学期中复习试卷(word版,含解析)
文档属性
| 名称 | 2020-2021学年湘教新版九年级下册数学期中复习试卷(word版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 355.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-26 22:37:27 | ||
图片预览



文档简介
2020-2021学年湘教新版九年级下册数学期中复习试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列各式中,计算正确的是( )
A.x+x3=x4
B.(x4)2=x6
C.x5?x2=x10
D.x8÷x2=x6(x≠0)
2.下列说法中正确的是( )
A.不循环小数是无理数
B.分数不是有理数
C.有理数都是有限小数
D.3.1415926是有理数
3.下列各分式中,是最简分式的是( )
A.
B.
C.
D.
4.下列说法正确的是( )
A.为了解湖南省中学生的心理健康情况,宜采用普查的方式
B.商场抽奖促销,中一等奖的概率是1%,则做100次这样的游戏一定会中一等奖
C.一组数据1,3,3,3,4,8的中位数和众数都是3
D.若甲、乙两个射击选手的平均成绩相同,且s甲2=0.01,s乙2=0.1,则应该选乙参赛
5.小明在边长为a的正方形硬纸板上挖去一个最大的圆,则剩余部分的面积是( )
A.a2﹣πa2
B.a2﹣πa2
C.(a2﹣πa2)
D.a2+πa2
6.下列式子为最简二次根式的是( )
A.
B.
C.
D.
7.下列函数中,对于任意实数x,y随x的增大而减小的是( )
A.y=x
B.y=
C.y=﹣x+2
D.y=2x2
8.将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为( )
A.y=(x+1)2﹣13
B.y=(x﹣5)2﹣5
C.y=(x﹣5)2﹣13
D.y=(x+1)2﹣5
9.关于x,y的方程组的解满足x+y>2,则a的取值范围为( )
A.a<﹣
B.a>﹣
C.a<
D.a>
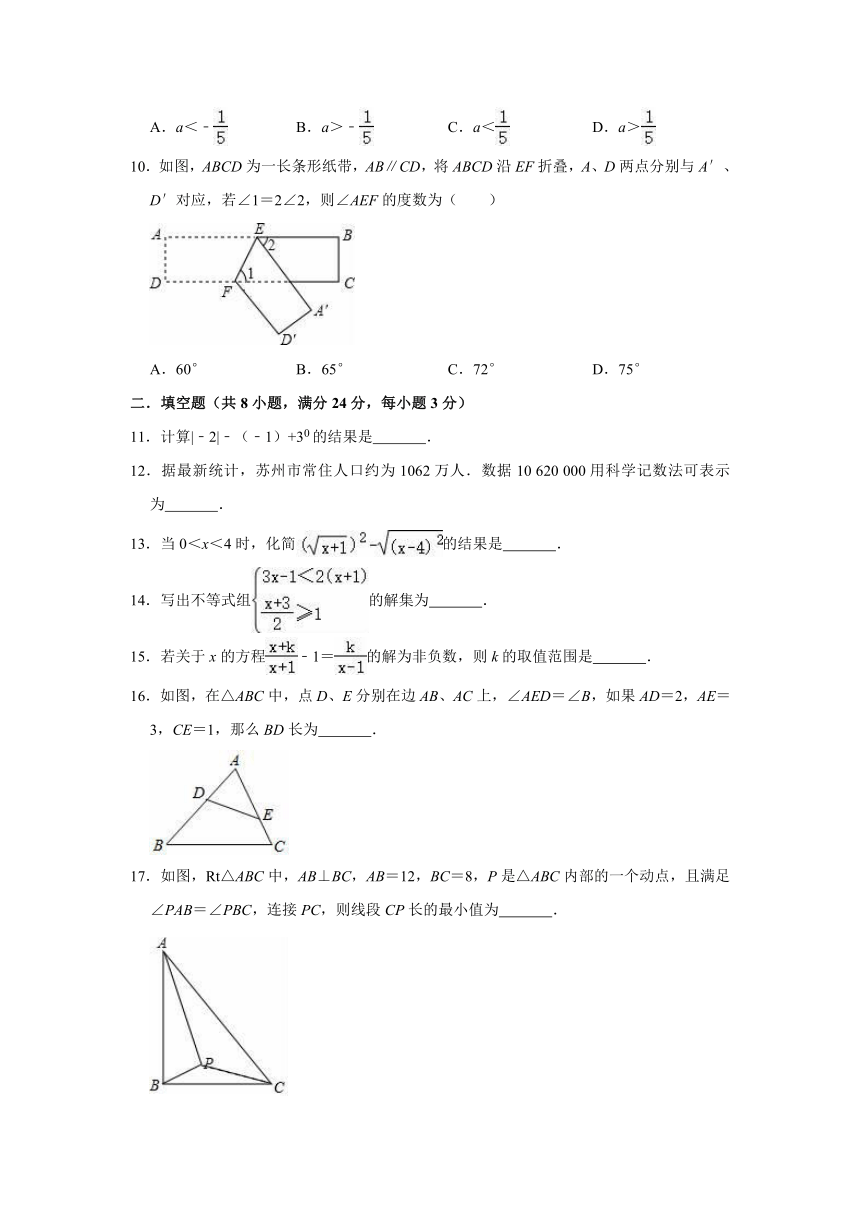
10.如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )
A.60°
B.65°
C.72°
D.75°
二.填空题(共8小题,满分24分,每小题3分)
11.计算|﹣2|﹣(﹣1)+30的结果是
.
12.据最新统计,苏州市常住人口约为1062万人.数据10
620
000用科学记数法可表示为
.
13.当0<x<4时,化简的结果是
.
14.写出不等式组的解集为
.
15.若关于x的方程﹣1=的解为非负数,则k的取值范围是
.
16.如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,如果AD=2,AE=3,CE=1,那么BD长为
.
17.如图,Rt△ABC中,AB⊥BC,AB=12,BC=8,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,连接PC,则线段CP长的最小值为
.
18.下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为
.
三.解答题(共8小题,满分66分)
19.计算:
(1);
(2).
20.解不等式组,并把它的解集在数轴上表示出来.
21.先化简,再求值:,其中a满足方程x2+5x+6=0.
22.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=100°,∠C=30°,求∠BDE的度数.
23.一个圆锥的母线长为10,底面半径为5,求这个圆锥的侧面积和全面积.
24.新型冠状病毒肺炎自2019年底爆发以来,经过全国人民的共同努力,已经在国内得到了有效控制,我国科学严格的防治措施也贏得了“世卫”组织的肯定和推广.为了有效地避免交叉感染,需要采取如戴口罩、勤洗手、少出门、重隔离等防护措施.复工初期,某公司为了解员工对防护措施的了解程度(包括“不了解、了解很少、基本了解和很了解”四项),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一
项),并将调查结果绘制成如图两幅统计图.
请你根据上面的信息,解答下列问题:
(1)本次共调查了
名员工,条形统计图中m=
.
(2)若该公司共有员工1000名,请你估计不了解防护措施的人数;
(3)在调查中,发现有4名员工的防护知识很全面,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内帮助普及防护知识,求恰好抽中一男一女的概率.
25.计算+++…+.
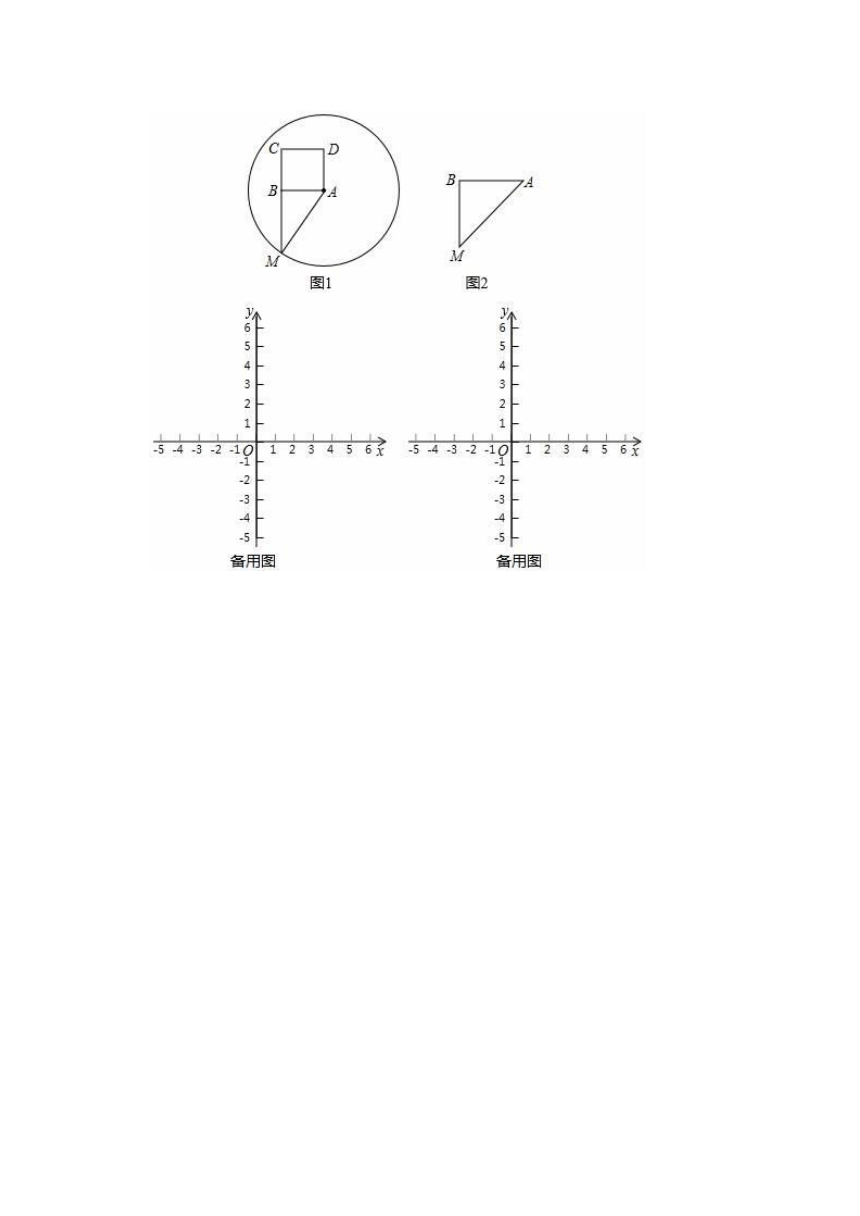
26.在△ABM中,∠ABM=90°,以AB为一边向△ABM的异侧作正方形ABCD,以A为圆心,AM为半径作⊙A,我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”,如果正方形ABCD恰好落在⊙A的内部(或圆上),我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”,
例如,图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”.
(1)图2中,△ABM中,BA=BM,∠ABM=90°,在图中画出⊙A的“关于△ABM的友好正方形ABCD”.
(2)若点A在反比例函数y=(k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(3)若点A是直线y=﹣x+2上的一个动点,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求出点A的横坐标m的取值范围.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、x+x3,无法合并,故此选项错误;
B、(x4)2=x8,故此选项错误;
C、x5?x2=x7,故此选项错误;
D、x8÷x2=x6(x≠0),正确.
故选:D.
2.解:A、无理数是无限不循环小数,故选项错误;
B、有理数包括分数,故选项错误;
C、无限循环小数也是有理数,故选项错误;
D、有限小数是有理数,故选项正确.
故选:D.
3.解:A、=,不符合题意;
B、=,不符合题意;
C、是最简分式,符合题意;
D、=,不符合题意;
故选:C.
4.解:A.由于河南省中学生数量较多,理解其心理健康情况没有必要普查,采取抽样调查较好,因此选项A不符合题意;
B.中一等奖的概率是1%,就是中一等奖的可能性为1%,并不一定100次这样的游戏一定会中奖,因此选项B不符合题意;
C.一组数据1,3,3,3,4,8,处在中间位置的两个数都是3,因此中位数是3,出现次数最多的是3,因此众数也是3,因此选项C符合题意;
D.若甲、乙两个射击选手的平均成绩相同,且s甲2=0.01,s乙2=0.1,由于0.01<0.1,甲比较稳定,因此选甲参赛比较合适,所以选项D不符合题意;
故选:C.
5.解:正方形的面积是a2;圆的面积是π()2=.
则剩余部分的面积是a2﹣πa2.
故选:B.
6.解:A、=|a+b|,不是最简二次根式,故本选项不符合题意;
B、=2,不是最简二次根式,故本选项不符合题意;
C、是最简二次根式,故本选项符合题意;
D、=,不是最简二次根式,故本选项不符合题意;
故选:C.
7.解:在y=x中,y随x的增大而增大,故选项A错误,
在y=中,在每个象限内,y随x的增大而减小,故选项B错误,
在y=﹣x+2中,y随x的增大而减小,故选项C正确,
在y=2x2中,x<0时,y随x的增大而减小,故选项D错误,
故选:C.
8.解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为y=(x﹣2+3)2﹣8+3,即y=(x+1)2﹣5.
故选:D.
9.解:∵,
∴②﹣①,得:4x+4y=7﹣5a,
∴x+y=,
∵x+y>2,
∴>2,
解得a<﹣,
故选:A.
10.解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=2∠2,设∠2=x,则∠AEF=∠1=∠FEA′=2x,
∴5x=180°,
∴x=36°,
∴∠AEF=2x=72°,
故选:C.
二.填空题(共8小题,满分24分,每小题3分)
11.解:原式=2+1+1=4,
故答案为:4
12.解:数据10
620
000用科学记数法可表示为1.062×107,
故答案为:1.062×107.
13.解:∵0<x<4,
∴=|x+1|+|x﹣4|=x+1+x﹣4=2x﹣3.
故答案为:2x﹣3.
14.解:不等式①的解集为x<3,
不等式②的解集为x≥﹣1,
所以不等式组的解集为﹣1≤x<3.
故答案为:﹣1≤x<3.
15.解:方程﹣1=,
(x+k)(x﹣1)﹣(x+1)(x﹣1)=k(x+1)
x2﹣x+kx﹣k﹣x2+1=kx+k
x=﹣2k+1
∵x≥0且x≠1,
∴﹣2k+1≥0且﹣2k+1≠1
解得k≤且k≠0.
故答案为k≤且k≠0.
16.解:∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC,
∴=,
∴=,
解得BD=4.
故答案为:4.
17.解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在Rt△BCO中,∵∠OBC=90°,BC=8,OB=6,
∴OC==10,
∴PC=OC﹣OP=10﹣6=4.
∴PC最小值为4.
故答案为:4.
18.解:分析题目可以知道:4=2×2,6=3×2,8=4×2,…;2=1+1,3=2+1,4=3+1,…;
∴18=2b,a=b﹣1;
∴b=9,a=8;
又∵9=(4﹣1)×(2+1),20=(6﹣1)×(3+1),35=(8﹣1)×(4+1),…;
∴x=(18﹣1)×(b+1)=17×10=170.
因此答案为:170.
三.解答题(共8小题,满分66分)
19.解:(1)原式=2×+3+﹣1﹣1
=+1+
=2+1;
(2)原式=?
=2a.
20.解:由①得x≥﹣2,
由②得x<,
∴不等式组的解集为>x≥﹣2.
不等式组的解集在数轴上表示如下:
.
21.解:
=?
=
=,
解方程x2+5x+6=0得:x=﹣2或﹣3,
∵分式中a不能为±2,0,
∴a=﹣3,
当a=﹣3时,原式==﹣.
22.(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=100°,∠C=30°,
∴∠ABC=180°﹣100°﹣30°=50°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=50°,∠BDE=∠EDF=25°.
23.解:这个圆锥的侧面积=×2π×5×10=50π;
这个圆锥的全面积=50π+π×52=75π.
24.解:(1)本次共调查的员工有:24÷40%=60(名);
基本了解的员工m=60﹣12﹣24﹣6=18(名);
故答案为:60,18;
(2)根据题意得:
1000×=200(名),
答:不了解防护措施的人数有200名;
(3)根据题意列表如下:
员工
男甲
男乙
男丙
女
男甲
男乙、男甲
男丙、男甲
女、男甲
男乙
男甲、男乙
男丙、男乙
女、男乙
男丙
男甲、男丙
男乙、男丙
女、男丙
女
男甲、女
男乙、女
男丙、女
共有12种等可能的情况数,其中恰好抽中一男一女的有6种,
则恰好抽中一男一女的概率为=.
25.解:原式=+++…+
=﹣1+﹣+﹣+…+﹣
=﹣1
=2﹣1.
26.(1)∵BA=BM,∠ABM=90°,
∴圆的半径AM=AB=AC,故点C在圆上,补全图形如图1,
(2)设A(2,a),
当a=2时,正方形ABCD
的顶点C恰好落在⊙A上(如图2);
当a>2时,正方形ABCD
的顶点均落在⊙A内部(如图3);
当a<2时,正方形ABCD
的顶点C落在⊙A外部(如图4);
∵反比例函数,
∴当a≥2时,则k≥4,
∴k的取值范围为:k≥4;
(3)当m=1时,正方形ABCD
的顶点C恰好落在⊙A上(如图5);
当0<m<1时,正方形ABCD
均落在⊙A内部(如图6);
当m=0时,△ABO
不存在;
当m<0时,正方形ABCD
均落在⊙A内部(如图7);
当m>1时,正方形ABCD
的顶点C落在⊙A外部(如图8),(当m=2时△ABO不存在);
综上分析,点A的横坐标m的取值范围为:0<m≤1或m<0.
一.选择题(共10小题,满分30分,每小题3分)
1.下列各式中,计算正确的是( )
A.x+x3=x4
B.(x4)2=x6
C.x5?x2=x10
D.x8÷x2=x6(x≠0)
2.下列说法中正确的是( )
A.不循环小数是无理数
B.分数不是有理数
C.有理数都是有限小数
D.3.1415926是有理数
3.下列各分式中,是最简分式的是( )
A.
B.
C.
D.
4.下列说法正确的是( )
A.为了解湖南省中学生的心理健康情况,宜采用普查的方式
B.商场抽奖促销,中一等奖的概率是1%,则做100次这样的游戏一定会中一等奖
C.一组数据1,3,3,3,4,8的中位数和众数都是3
D.若甲、乙两个射击选手的平均成绩相同,且s甲2=0.01,s乙2=0.1,则应该选乙参赛
5.小明在边长为a的正方形硬纸板上挖去一个最大的圆,则剩余部分的面积是( )
A.a2﹣πa2
B.a2﹣πa2
C.(a2﹣πa2)
D.a2+πa2
6.下列式子为最简二次根式的是( )
A.
B.
C.
D.
7.下列函数中,对于任意实数x,y随x的增大而减小的是( )
A.y=x
B.y=
C.y=﹣x+2
D.y=2x2
8.将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为( )
A.y=(x+1)2﹣13
B.y=(x﹣5)2﹣5
C.y=(x﹣5)2﹣13
D.y=(x+1)2﹣5
9.关于x,y的方程组的解满足x+y>2,则a的取值范围为( )
A.a<﹣
B.a>﹣
C.a<
D.a>
10.如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )
A.60°
B.65°
C.72°
D.75°
二.填空题(共8小题,满分24分,每小题3分)
11.计算|﹣2|﹣(﹣1)+30的结果是
.
12.据最新统计,苏州市常住人口约为1062万人.数据10
620
000用科学记数法可表示为
.
13.当0<x<4时,化简的结果是
.
14.写出不等式组的解集为
.
15.若关于x的方程﹣1=的解为非负数,则k的取值范围是
.
16.如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,如果AD=2,AE=3,CE=1,那么BD长为
.
17.如图,Rt△ABC中,AB⊥BC,AB=12,BC=8,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,连接PC,则线段CP长的最小值为
.
18.下列各正方形中的四个数之间都有相同的规律,根据此规律,x的值为
.
三.解答题(共8小题,满分66分)
19.计算:
(1);
(2).
20.解不等式组,并把它的解集在数轴上表示出来.
21.先化简,再求值:,其中a满足方程x2+5x+6=0.
22.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=100°,∠C=30°,求∠BDE的度数.
23.一个圆锥的母线长为10,底面半径为5,求这个圆锥的侧面积和全面积.
24.新型冠状病毒肺炎自2019年底爆发以来,经过全国人民的共同努力,已经在国内得到了有效控制,我国科学严格的防治措施也贏得了“世卫”组织的肯定和推广.为了有效地避免交叉感染,需要采取如戴口罩、勤洗手、少出门、重隔离等防护措施.复工初期,某公司为了解员工对防护措施的了解程度(包括“不了解、了解很少、基本了解和很了解”四项),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一
项),并将调查结果绘制成如图两幅统计图.
请你根据上面的信息,解答下列问题:
(1)本次共调查了
名员工,条形统计图中m=
.
(2)若该公司共有员工1000名,请你估计不了解防护措施的人数;
(3)在调查中,发现有4名员工的防护知识很全面,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内帮助普及防护知识,求恰好抽中一男一女的概率.
25.计算+++…+.
26.在△ABM中,∠ABM=90°,以AB为一边向△ABM的异侧作正方形ABCD,以A为圆心,AM为半径作⊙A,我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”,如果正方形ABCD恰好落在⊙A的内部(或圆上),我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”,
例如,图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”.
(1)图2中,△ABM中,BA=BM,∠ABM=90°,在图中画出⊙A的“关于△ABM的友好正方形ABCD”.
(2)若点A在反比例函数y=(k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(3)若点A是直线y=﹣x+2上的一个动点,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求出点A的横坐标m的取值范围.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、x+x3,无法合并,故此选项错误;
B、(x4)2=x8,故此选项错误;
C、x5?x2=x7,故此选项错误;
D、x8÷x2=x6(x≠0),正确.
故选:D.
2.解:A、无理数是无限不循环小数,故选项错误;
B、有理数包括分数,故选项错误;
C、无限循环小数也是有理数,故选项错误;
D、有限小数是有理数,故选项正确.
故选:D.
3.解:A、=,不符合题意;
B、=,不符合题意;
C、是最简分式,符合题意;
D、=,不符合题意;
故选:C.
4.解:A.由于河南省中学生数量较多,理解其心理健康情况没有必要普查,采取抽样调查较好,因此选项A不符合题意;
B.中一等奖的概率是1%,就是中一等奖的可能性为1%,并不一定100次这样的游戏一定会中奖,因此选项B不符合题意;
C.一组数据1,3,3,3,4,8,处在中间位置的两个数都是3,因此中位数是3,出现次数最多的是3,因此众数也是3,因此选项C符合题意;
D.若甲、乙两个射击选手的平均成绩相同,且s甲2=0.01,s乙2=0.1,由于0.01<0.1,甲比较稳定,因此选甲参赛比较合适,所以选项D不符合题意;
故选:C.
5.解:正方形的面积是a2;圆的面积是π()2=.
则剩余部分的面积是a2﹣πa2.
故选:B.
6.解:A、=|a+b|,不是最简二次根式,故本选项不符合题意;
B、=2,不是最简二次根式,故本选项不符合题意;
C、是最简二次根式,故本选项符合题意;
D、=,不是最简二次根式,故本选项不符合题意;
故选:C.
7.解:在y=x中,y随x的增大而增大,故选项A错误,
在y=中,在每个象限内,y随x的增大而减小,故选项B错误,
在y=﹣x+2中,y随x的增大而减小,故选项C正确,
在y=2x2中,x<0时,y随x的增大而减小,故选项D错误,
故选:C.
8.解:∵y=x2﹣4x﹣4=(x﹣2)2﹣8,
∴将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移3个单位,得到抛物线的表达式为y=(x﹣2+3)2﹣8+3,即y=(x+1)2﹣5.
故选:D.
9.解:∵,
∴②﹣①,得:4x+4y=7﹣5a,
∴x+y=,
∵x+y>2,
∴>2,
解得a<﹣,
故选:A.
10.解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=2∠2,设∠2=x,则∠AEF=∠1=∠FEA′=2x,
∴5x=180°,
∴x=36°,
∴∠AEF=2x=72°,
故选:C.
二.填空题(共8小题,满分24分,每小题3分)
11.解:原式=2+1+1=4,
故答案为:4
12.解:数据10
620
000用科学记数法可表示为1.062×107,
故答案为:1.062×107.
13.解:∵0<x<4,
∴=|x+1|+|x﹣4|=x+1+x﹣4=2x﹣3.
故答案为:2x﹣3.
14.解:不等式①的解集为x<3,
不等式②的解集为x≥﹣1,
所以不等式组的解集为﹣1≤x<3.
故答案为:﹣1≤x<3.
15.解:方程﹣1=,
(x+k)(x﹣1)﹣(x+1)(x﹣1)=k(x+1)
x2﹣x+kx﹣k﹣x2+1=kx+k
x=﹣2k+1
∵x≥0且x≠1,
∴﹣2k+1≥0且﹣2k+1≠1
解得k≤且k≠0.
故答案为k≤且k≠0.
16.解:∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC,
∴=,
∴=,
解得BD=4.
故答案为:4.
17.解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在Rt△BCO中,∵∠OBC=90°,BC=8,OB=6,
∴OC==10,
∴PC=OC﹣OP=10﹣6=4.
∴PC最小值为4.
故答案为:4.
18.解:分析题目可以知道:4=2×2,6=3×2,8=4×2,…;2=1+1,3=2+1,4=3+1,…;
∴18=2b,a=b﹣1;
∴b=9,a=8;
又∵9=(4﹣1)×(2+1),20=(6﹣1)×(3+1),35=(8﹣1)×(4+1),…;
∴x=(18﹣1)×(b+1)=17×10=170.
因此答案为:170.
三.解答题(共8小题,满分66分)
19.解:(1)原式=2×+3+﹣1﹣1
=+1+
=2+1;
(2)原式=?
=2a.
20.解:由①得x≥﹣2,
由②得x<,
∴不等式组的解集为>x≥﹣2.
不等式组的解集在数轴上表示如下:
.
21.解:
=?
=
=,
解方程x2+5x+6=0得:x=﹣2或﹣3,
∵分式中a不能为±2,0,
∴a=﹣3,
当a=﹣3时,原式==﹣.
22.(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=100°,∠C=30°,
∴∠ABC=180°﹣100°﹣30°=50°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=50°,∠BDE=∠EDF=25°.
23.解:这个圆锥的侧面积=×2π×5×10=50π;
这个圆锥的全面积=50π+π×52=75π.
24.解:(1)本次共调查的员工有:24÷40%=60(名);
基本了解的员工m=60﹣12﹣24﹣6=18(名);
故答案为:60,18;
(2)根据题意得:
1000×=200(名),
答:不了解防护措施的人数有200名;
(3)根据题意列表如下:
员工
男甲
男乙
男丙
女
男甲
男乙、男甲
男丙、男甲
女、男甲
男乙
男甲、男乙
男丙、男乙
女、男乙
男丙
男甲、男丙
男乙、男丙
女、男丙
女
男甲、女
男乙、女
男丙、女
共有12种等可能的情况数,其中恰好抽中一男一女的有6种,
则恰好抽中一男一女的概率为=.
25.解:原式=+++…+
=﹣1+﹣+﹣+…+﹣
=﹣1
=2﹣1.
26.(1)∵BA=BM,∠ABM=90°,
∴圆的半径AM=AB=AC,故点C在圆上,补全图形如图1,
(2)设A(2,a),
当a=2时,正方形ABCD
的顶点C恰好落在⊙A上(如图2);
当a>2时,正方形ABCD
的顶点均落在⊙A内部(如图3);
当a<2时,正方形ABCD
的顶点C落在⊙A外部(如图4);
∵反比例函数,
∴当a≥2时,则k≥4,
∴k的取值范围为:k≥4;
(3)当m=1时,正方形ABCD
的顶点C恰好落在⊙A上(如图5);
当0<m<1时,正方形ABCD
均落在⊙A内部(如图6);
当m=0时,△ABO
不存在;
当m<0时,正方形ABCD
均落在⊙A内部(如图7);
当m>1时,正方形ABCD
的顶点C落在⊙A外部(如图8),(当m=2时△ABO不存在);
综上分析,点A的横坐标m的取值范围为:0<m≤1或m<0.
同课章节目录
