上海市杨浦区2020-2021学年七年级下学期期中数学试卷(Word版无答案)
文档属性
| 名称 | 上海市杨浦区2020-2021学年七年级下学期期中数学试卷(Word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-27 09:18:24 | ||
图片预览


文档简介
2020-2021学年上海市杨浦区七年级(下)期中数学试卷
一、填空题(本大题共14题,每题2分,满分28分)
1.27的立方根是
.
2.若x4=625,则x=
.
3.把化成幂的形式是
.
4.比较大小:﹣3
﹣2(填“>”、“=”或“<”).
5.计算:()=
.
6.随着国内疫情防控形势持续向好,清明小长假期间旅客探亲、祭祖、踏青等出行需求旺盛.4月2日至5日,全国铁路预计发送旅客约49700000人次,请将49700000这个数保留两个有效数字并用科学记数法表示为
.
7.已知数轴上A、B两点间的距离为,如果点A所表示的数是﹣1,那么点B所表示的数是
.
8.如图,直线AB、CD相交于点O,如果∠AOD=140°,那么直线AB与CD的夹角是
.
9.如图,已知a∥b,如果∠1=70°,∠2=35°,那么∠3=
度.
10.如图,已知直线AD∥BC,如果△BCD的面积是6平方厘米,BC=4厘米,那么△ABC中BC边上的高是
厘米.
11.如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=55°,那么∠AOD=
度.
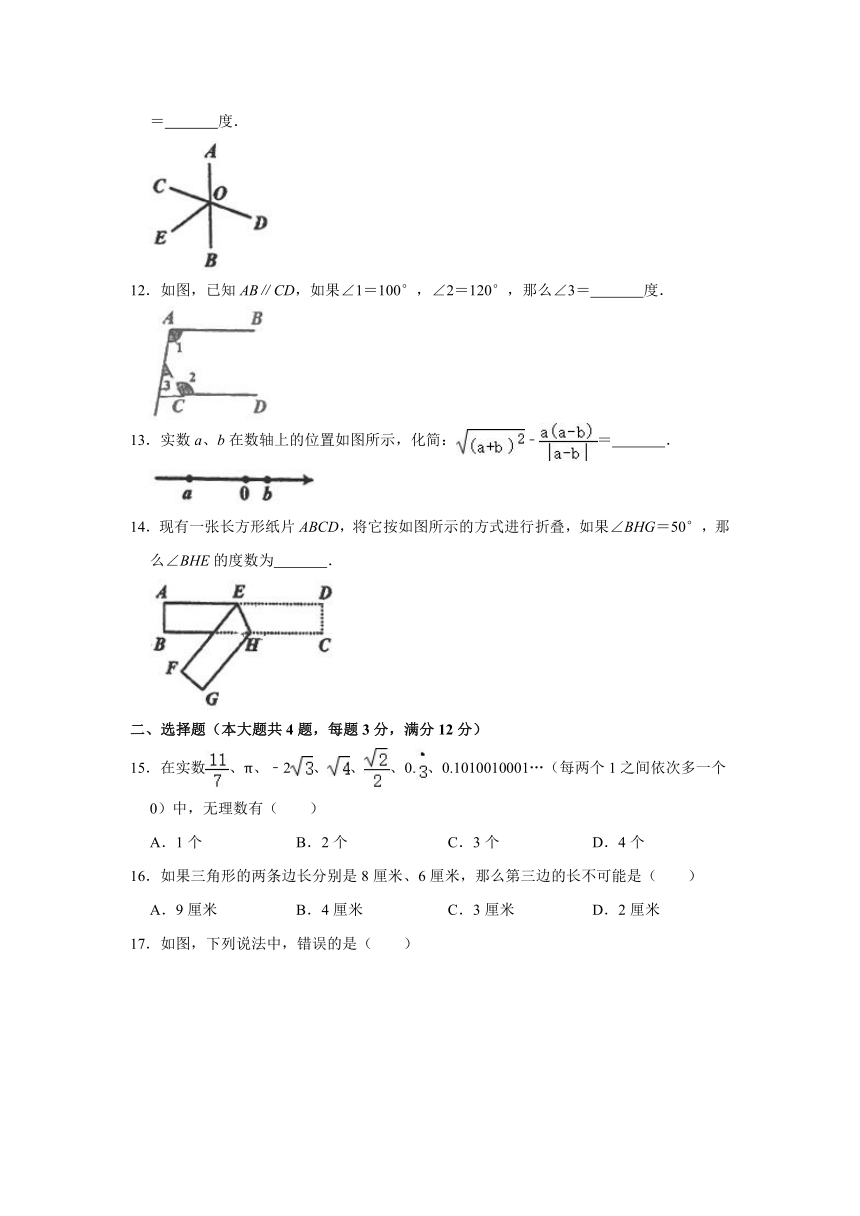
12.如图,已知AB∥CD,如果∠1=100°,∠2=120°,那么∠3=
度.
13.实数a、b在数轴上的位置如图所示,化简:﹣=
.
14.现有一张长方形纸片ABCD,将它按如图所示的方式进行折叠,如果∠BHG=50°,那么∠BHE的度数为
.
二、选择题(本大题共4题,每题3分,满分12分)
15.在实数、π、﹣2、、、0.、0.1010010001…(每两个1之间依次多一个0)中,无理数有( )
A.1个
B.2个
C.3个
D.4个
16.如果三角形的两条边长分别是8厘米、6厘米,那么第三边的长不可能是( )
A.9厘米
B.4厘米
C.3厘米
D.2厘米
17.如图,下列说法中,错误的是( )
A.∠3和∠4是邻补角
B.∠1和∠2是同旁内角
C.∠1和∠5是同位角
D.∠5和∠6是内错角
18.下列说法中,正确的有( )
①过一点有且只有一条直线与己知直线平行
②从直线外一点到直线的垂线段叫做点到直线的距离
③两平行线间距离处处相等
④平行于同一直线的两直线互相平行.
A.1个
B.2个
C.3个
D.4个
三、计算题(本大题共4题,每题6分,满分24分)
19.计算:﹣(﹣)﹣.
20.计算:3÷×﹣.
21.计算:+(2+)0×()﹣1.
22.利用幕的运算性质进行计算:×÷×8.
四、解答题(本大题共3题,每题6分,满分18分)
23.按要求完成作图并填空:
(1)作CABC的平分线,交边AC于点D(尺规作图,保留作图痕迹);
(2)过点A画直线BC的垂线,交直线BC于点E,那么点A到直线BC的距离是线段
的长;
(3)在(2)的条件下,如果∠ABC=135°,点B恰好是CE的中点,BC=2cm,那么S△ABC=
cm2.
24.如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB
(
),
所以∠1+
=180°
(
).
因为∠1=∠A(已知),
所以∠A+
=180°
(
).
所以DE∥AC
(
).
25.如图,已知AB∥CD,直线MN分别交直线AB、CD于点E、F,射线EG、FH分别平分∠AEF、∠DFE,试说明EG∥FH的理由.
解:因为AB∥CD(已知),
所以∠AEF=∠DFE(
),
因为射线EG、FH分别平分∠AEF、∠DFE(已知),
所以∠
=∠AEF,
∠
=∠EFD
(
).
所以
(等式性质).
所以EG∥FH(
).
五、综合题(本大题共3题,每题6分,满分18分)
26.如图,已知∠1=∠2,∠D=90°,EF⊥CD,试说明∠3=∠B的理由.
27.阅读下面的文字,解答问题.
对于实数a,我们规定:用符号[a]表示不大于a的最大整数;用{a}表示a减去[a]所得的差.
例如:[]=1,[2.2]=2,{}=﹣1,{2.2}=2.2﹣2=0.2.
(1)仿照以上方法计算:[]=_
{5﹣}=
;
(2)若[]=1,写出所有满足题意的整数x的值:
.
(3)已知y0是一个不大于280的非负数,且满足{}=0.我们规定:y1=[],y2=[],y3=[],……,以此类推,直到yn第一次等于1时停止计算.当y0是符合条件的所有数中的最大数时,此时y0=
,n=
.
28.已知:AB∥CD,截线MN分别交AB、CD于点M、N.
(1)如图①,点B在线段MN上,设∠EBM=α°,∠DNM=β°,且满足+(β﹣60)2=0,求∠BEM的度数;
(2)如图②,在(1)的条件下,射线DF平分∠CDE,且交线段BE的延长线于点F;请写出∠DEF与∠CDF之间的数量关系,并说明理由;
(3)如图③,当点P在射线NT上运动时,∠DCP与∠BMT的平分线交于点Q,则∠Q与∠CPM的比值为
(直接写出答案).
一、填空题(本大题共14题,每题2分,满分28分)
1.27的立方根是
.
2.若x4=625,则x=
.
3.把化成幂的形式是
.
4.比较大小:﹣3
﹣2(填“>”、“=”或“<”).
5.计算:()=
.
6.随着国内疫情防控形势持续向好,清明小长假期间旅客探亲、祭祖、踏青等出行需求旺盛.4月2日至5日,全国铁路预计发送旅客约49700000人次,请将49700000这个数保留两个有效数字并用科学记数法表示为
.
7.已知数轴上A、B两点间的距离为,如果点A所表示的数是﹣1,那么点B所表示的数是
.
8.如图,直线AB、CD相交于点O,如果∠AOD=140°,那么直线AB与CD的夹角是
.
9.如图,已知a∥b,如果∠1=70°,∠2=35°,那么∠3=
度.
10.如图,已知直线AD∥BC,如果△BCD的面积是6平方厘米,BC=4厘米,那么△ABC中BC边上的高是
厘米.
11.如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=55°,那么∠AOD=
度.
12.如图,已知AB∥CD,如果∠1=100°,∠2=120°,那么∠3=
度.
13.实数a、b在数轴上的位置如图所示,化简:﹣=
.
14.现有一张长方形纸片ABCD,将它按如图所示的方式进行折叠,如果∠BHG=50°,那么∠BHE的度数为
.
二、选择题(本大题共4题,每题3分,满分12分)
15.在实数、π、﹣2、、、0.、0.1010010001…(每两个1之间依次多一个0)中,无理数有( )
A.1个
B.2个
C.3个
D.4个
16.如果三角形的两条边长分别是8厘米、6厘米,那么第三边的长不可能是( )
A.9厘米
B.4厘米
C.3厘米
D.2厘米
17.如图,下列说法中,错误的是( )
A.∠3和∠4是邻补角
B.∠1和∠2是同旁内角
C.∠1和∠5是同位角
D.∠5和∠6是内错角
18.下列说法中,正确的有( )
①过一点有且只有一条直线与己知直线平行
②从直线外一点到直线的垂线段叫做点到直线的距离
③两平行线间距离处处相等
④平行于同一直线的两直线互相平行.
A.1个
B.2个
C.3个
D.4个
三、计算题(本大题共4题,每题6分,满分24分)
19.计算:﹣(﹣)﹣.
20.计算:3÷×﹣.
21.计算:+(2+)0×()﹣1.
22.利用幕的运算性质进行计算:×÷×8.
四、解答题(本大题共3题,每题6分,满分18分)
23.按要求完成作图并填空:
(1)作CABC的平分线,交边AC于点D(尺规作图,保留作图痕迹);
(2)过点A画直线BC的垂线,交直线BC于点E,那么点A到直线BC的距离是线段
的长;
(3)在(2)的条件下,如果∠ABC=135°,点B恰好是CE的中点,BC=2cm,那么S△ABC=
cm2.
24.如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB
(
),
所以∠1+
=180°
(
).
因为∠1=∠A(已知),
所以∠A+
=180°
(
).
所以DE∥AC
(
).
25.如图,已知AB∥CD,直线MN分别交直线AB、CD于点E、F,射线EG、FH分别平分∠AEF、∠DFE,试说明EG∥FH的理由.
解:因为AB∥CD(已知),
所以∠AEF=∠DFE(
),
因为射线EG、FH分别平分∠AEF、∠DFE(已知),
所以∠
=∠AEF,
∠
=∠EFD
(
).
所以
(等式性质).
所以EG∥FH(
).
五、综合题(本大题共3题,每题6分,满分18分)
26.如图,已知∠1=∠2,∠D=90°,EF⊥CD,试说明∠3=∠B的理由.
27.阅读下面的文字,解答问题.
对于实数a,我们规定:用符号[a]表示不大于a的最大整数;用{a}表示a减去[a]所得的差.
例如:[]=1,[2.2]=2,{}=﹣1,{2.2}=2.2﹣2=0.2.
(1)仿照以上方法计算:[]=_
{5﹣}=
;
(2)若[]=1,写出所有满足题意的整数x的值:
.
(3)已知y0是一个不大于280的非负数,且满足{}=0.我们规定:y1=[],y2=[],y3=[],……,以此类推,直到yn第一次等于1时停止计算.当y0是符合条件的所有数中的最大数时,此时y0=
,n=
.
28.已知:AB∥CD,截线MN分别交AB、CD于点M、N.
(1)如图①,点B在线段MN上,设∠EBM=α°,∠DNM=β°,且满足+(β﹣60)2=0,求∠BEM的度数;
(2)如图②,在(1)的条件下,射线DF平分∠CDE,且交线段BE的延长线于点F;请写出∠DEF与∠CDF之间的数量关系,并说明理由;
(3)如图③,当点P在射线NT上运动时,∠DCP与∠BMT的平分线交于点Q,则∠Q与∠CPM的比值为
(直接写出答案).
同课章节目录
